热塑性纤维金属层合板舱内爆炸响应数值模拟

周 沪，孔祥韶，刘 芳，郑 成

（1. 武汉理工大学绿色智能江海直达船舶与邮轮游艇研究中心，湖北 武汉 430063；2. 武汉理工大学交通与物流工程学院，湖北 武汉 430063）

在爆炸、冲击等极端动态载荷作用下，伴随着材料经历塑性大变形、损伤至断裂的整个过程，受载结构将发生严重的破坏，从而导致灾难性的后果，此类动态冲击载荷和结构响应过程受到人们的极大关注，也是近年来研究的前沿和热点。纤维金属层合板是由高强纤维增强复合材料与金属薄层交互叠合，在一定温度、压力下层压而成的超混杂复合结构材料，其继承了金属与纤维增强复合材料的优点[1]，并有效地弥补了二者的不足，在同等条件下的力学性能优于单一金属[2-4]与复合材料板[5]。金属层对复合材料层起到了保护作用，而纤维层可以通过多样的失效模式有效地吸收动力载荷能量，使纤维金属层合板具有优异的整体力学性能。

研究表明，纤维增强金属层合板的各种失效模式在低速冲击下的吸能贡献比例并不是固定的[6]，会受到金属层材料[7-10]、纤维层材料[11]、组分体积分数[12-17]、铺层顺序与位置[6]以及连接层强度[18]等诸多因素的影响。设计人员可以通过合理地设计层合板参数来调整各组分间的吸能贡献比例，进而设计出适用于不同工作环境的层合板结构[19]。但层合板在高速冲击以及爆炸载荷作用下的响应规律研究仍处于初期阶段，对于具有更优良抗爆抗冲击潜力的热塑性纤维增强金属层合板的研究相对较少[20-21]，对其在强动力载荷作用下的失效机理研究没有得到相对统一的结论。

对于舱内爆炸问题，除了初始爆炸冲击波的作用外，壁面反射冲击波和准静态压力也是重要的毁伤方式。舱内爆炸载荷对结构产生的毁伤效应更加严重[22]，其产生的破坏效应取决于封闭结构的材料、几何参数，炸药的种类、质量等诸多因素[23]。

本研究以热塑性纤维增强金属层合板为研究对象，基于封闭空间内爆炸载荷作用下层合板动态响应试验数据以及通过代表体积元（representative volume element, RVE）方法计算得到的纤维板材料参数，开展热塑性纤维增强金属层合板的数值模拟研究。

1 热塑性纤维金属层合板舱内爆炸响应试验

1.1 试验布置与工况

试验中使用的层合板由热塑性玻璃纤维增强塑料（fiber glass reinforced plastics，GFRP）与铝合金（2024-O）有序交叠热压而成，铝板厚度为0.5 mm，玻璃纤维层（3 层纤维布）厚度为1.0 mm。本研究中使用的层合板由5 层铝合金板与4 层纤维层叠合而成，编号为A5G4。考虑到金属与热塑性材料间的黏接问题，在二者间增加一层厚度为40 μm 的聚丙烯（PP）热压膜，同时对铝板表面进行氧化处理，以增强连接界面的韧性。具体铺层形式如图1 所示。加工时，首先将交替叠合铺放的金属层与纤维层在30 min 内加热到200 ℃，使热塑性基体熔化；然后通过液压装置在板面上均匀施加0.55 MPa 的压力并保压；最后以5 ℃/min 的速度降温至室温冷却，完成热压成型过程。所有层合板均通过上述加工工艺完成，批次间无其他明显差异。将层合板热压成型后，切割成尺寸为300 mm×300 mm的试件备用。

图1 热塑性纤维增强金属层合板铺层形式Fig. 1 Lay-up of fiber reinforced thermoplastic and metal laminate

试验装置为两端开口的刚性箱体，通过夹持装置将试件固定在两端，以形成封闭环境。试验过程中，一端使用20 mm 厚的钢板夹持密封，另一端夹持层合板作为目标靶板。在箱体顶部悬挂圆柱形TNT 炸药于箱体中心位置，通过顶部的小孔引出导线引爆，装置具体形式如图2 所示。箱体内部尺寸为405 mm×180 mm×180 mm，即实际舱内爆炸载荷作用在层合板上的范围为180 mm×180 mm。层合板通过16 个M16 的螺栓与箱体紧密相连，外部通过20 mm 厚的钢板夹持边缘部分。整体装置通过若干槽钢形成的工装固定在水泥基座上，试验中整体装置的具体架设情况如图3 所示。

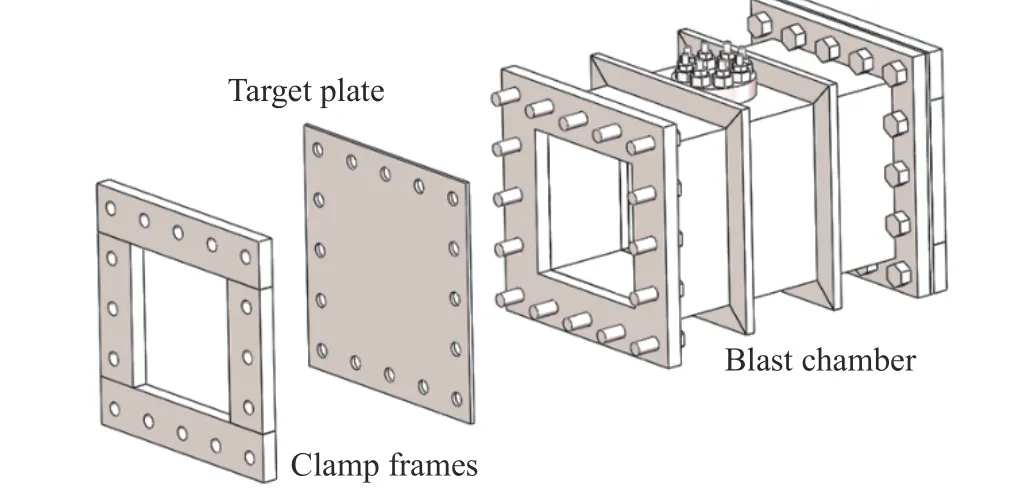
图2 封闭箱体示意图Fig. 2 Schematic diagram of enclosed cabin

图3 试验过程中整体装置架设Fig. 3 Set-up of the tests

试验前，对每块层合板进行实际称重与厚度测量，详细统计每块试件对应装药的质量与几何尺寸，结果如表1 所示。其中：m为试件质量，d为试件厚度，W为装药量，D为药柱直径，h为药柱高度。在具体试验中，使用雷管起爆TNT 炸药，雷管当量可等效为1 g 的TNT 炸药。

表1 试验工况Table 1 Test conditions

1.2 试验结果

试验中，通过高速三维数字图像相关（digital image correlation, DIC）系统实时记录层合板的响应过程，高速摄影仪拍摄频率为3×104s-1。由于层合板实际响应情况未知，试验前无法明确判断具体工况是否会发生整体破坏，因此先开展大装药量试验，确定层合板不会发生整体破坏后，再使用DIC 设备对层合板的小药量工况进行测试。部分未能获得变形历程数据的工况在试验完成后通过三维扫描仪获得最终变形。统计不同工况下层合板中心点的最终变形响应结果，如表2 所示，其中δmax为最大挠度。

表2 层合板试验变形数据Table 2 Deformation of the laminate

装药量从5 g 逐渐变化到50 g 的过程中，明显存在2 个阶段，即在10～20 g 装药量之间，最大挠度的线性关系存在斜率变化，将整个变形趋势分为两部分：(1) 在20～50 g 装药量下，层合板变形保持着较好的线性；(2) 在5～10 g 装药量下，对比大装药量下的变化趋势，小装药量下的变形明显偏大。其中，在5 g 装药下，装药量W与封闭舱室体积（Vc）的比值为0.381 kg/m3，即W/Vc＜ 0.387 kg/m3[24]，此时爆炸产物的燃烧效应不可忽略，燃烧效应使得装药能量进一步释放，导致层合板中心点的变形偏大；此外，在5 g 装药下，可等效为1 g 装药的雷管也是变形的重要影响因素，变形偏大应是上述两个因素综合作用的结果。但在10 g 装药下，由于W/Vc偏大，燃烧效应不明显，导致这一结果的原因应该与层合板变形模式有关，需要进一步分析。

爆炸载荷作用下层合板整体会出现大变形，变形的最大值出现在板的中心位置。此时，由于铝板与纤维板的延展性存在差异，铝板产生了塑性变形而并没有明显断裂，纤维板则在其中发生了大面积失效断裂。进一步开展X 射线断层扫描，在不破坏试件的情况下，断层扫描可以提供结构内部的横截面图像。为了满足断层扫描设备的尺寸要求，需要将层合板夹持部分边缘各切割50 mm，即得到200 mm×200 mm 的扫描件，同时并不会对层合板受载区域造成二次破坏。

图4 为典型的层合板在舱内爆炸载荷下截面方向内部破坏模式。从图4 可以看出，中心点变形最大，且最外层铝板出现明显的“鼓包”。同时可以看到，内部纤维出现了明显的断裂失效，失效主要发生在层合板中心区域与夹持边界周围，但需要注意的是，分层主要发生在纤维与金属之间，纤维间的分层现象并不明显。进一步观察还可以发现，最外层纤维层的断裂最明显，产生这一结果的原因主要是层合板的大变形使最外层纤维产生较大的应变，这与低速冲击下的损伤[2,25-27]明显不同，低速冲击下，损伤最明显的是受载一侧的纤维层。

图4 截面典型破坏模式Fig. 4 Typical damage mode (sectional view)

由表3 可以看出：随着变形的逐渐增大，板中心点变形逐渐增大，夹持区域的破坏范围也逐渐增大；当药量较小时，层合板内部基本没有发生分层的现象；当药量为30 g 时，分层首先出现在板中心点以及夹持区域附近，且都是背爆面的外层先分层；随着药量进一步增大，分层的范围进一步扩大，当药量为40 g 时，分层的区域基本遍布整块板；药量增大到50 g 时，中心点“鼓包”范围内的纤维板均已失效，此时最外层铝板失去了层间连接，表现为更显著的凸起。

表3 药量递增下截面破坏形式变化Table 3 Damage mode under different charge (sectional view)

2 热塑性纤维金属层合板数值模拟

2.1 纤维层材料参数计算

复合材料可以看作是由一个最小构成单元周期性排布而成，因此，可以通过某种方法用这个最小单元来体现整体复合材料的性能，该最小单元称之为代表体积元（representative volume element，RVE）。在找到这样的最小单元后，最棘手的问题是如何让这个最小单元在受力变形后还能够达到周期性分布，进而表征出宏观属性。为了达到这一目的，这个最小单元受力后在边界上必须能够连续，即复合材料内的每个代表体积元都应具有相同的变形模式，且不会发生分离与重叠。

周期性边界（periodicity boundary）被用来施加在选取的代表体积元上。对于满足周期性边界的六面体代表体积元，对应面相同位置的变形强制保持一致，这样就可以满足受力后结构还可以在3 个方向上周期性延伸，以达到用最小单元模拟宏观材料属性的目的。式中：V为代表体积元的体积，S为代表体积元的边界面积，ui为第i个组分的位移，nj为垂直于S的第j个分量。

在不同边界面上赋予不同形式的强制变形后，就可以求解代表体积元的外力做功与应变能。进一步可以表示出各方向的平均应力，在获取了应力与应变后就可以求解不同方向的模量。

本研究所用的复合材料板由铝合金与热塑性玻璃纤维预浸料交替叠合而成，铝板的材料属性可通过传统材料性能试验得到，预浸料的性能将通过上述的代表体积元法获得。

图5 所示为编织纤维布在不同尺度的构成关系。纤维丝聚集成束，间隙中被填充满树脂基体，形成具有一定形状的单股纤维束；将纤维束按照一定的交替方式编织成型，在编织过程中，纤维束具有新的截面形状与空间分布；在干纤维布的空隙填充树脂基体，形成单层纤维预浸料；与金属板交替铺排后热压成型，形成试验所用的热塑性纤维增强金属板。通过测量纤维丝、纤维束等基本组成结构的几何参数，作为有限元计算输入参数，可以得到试验所用编织纤维布的宏观材料参数。

将单层纤维布置于三维超景深光学显微镜下观察，放大100 倍后，得到如图6(a)所示的纤维编织形式，可以看出试验所用纤维布为1/7 编织的正交缎纹布，缎纹布的编织方法如图6(b)所示，其中黑色和白色分别代表当前视角下可见的经线与纬线。

图6 纤维布编织方法Fig. 6 Fiber of weaving method

在纤维布截面方向，经500 倍放大后可以看到纤维丝级别的更细观结构形式，如图7 所示，在显微镜下直接测量得到若干组纤维丝的直径，取不同位置的多组测量值，计算平均值，作为纤维直径。

图7 玻璃纤维截面Fig. 7 Cross section of glass fiber

在纤维布截面方向，经100 倍放大后在更大视野范围观察，可以看到纤维布中纤维束的几何形式，如图8 所示，其中明亮的曲线为经向纤维束，椭圆形的截面为纬向纤维束，多次测量椭圆截面的长轴和短轴数据，以平均值作为纤维束截面尺寸。最终的细观结构几何参数如表4 所示。对于构成预浸料的玻璃纤维与树脂基体，使用厂家提供的基本性能参数作为输入参数，具体参数如表5 所示。其中： ρf为复合材料的密度，E为杨氏模量，μ为泊松比，w为质量分数。

表4 复合材料内部纤维的几何参数Table 4 Fiber geometrical parameters of the laminate

表5 复合材料的组成及其力学性能参数Table 5 Composition of the laminate and their mechanical parameters

图8 纤维束截面Fig. 8 Cross section of fiber yarn

按照上述得到的细观参数建立复合材料的代表体积元模型，如图9 所示，总共划分六面体网格250 000 个。采用已验证的计算方法求解试验中复合材料的性能参数，作为后续计算的输入参数，计算结果如表6 所示。其中：E11、E22、E33分别为3 个方向的拉伸模量，G12、G13、G23分别为3 个方向的剪切模量，μ12、μ13、μ32分别为3 个方向的泊松比。

图9 代表体积元模型Fig. 9 Representative volume element model

表6 复合材料性能参数Table 6 Mechanical parameters of the laminate

2.2 舱内爆炸响应数值模拟

采用ANSYS-AUTODYN 非线性显式动力学程序模拟层合板的舱内爆炸响应，数值模拟过程中使用拉格朗日 -欧拉耦合方法模拟TNT 起爆产生的强冲击波作用到层合板上的过程，并与试验结果进行对比分析。

2.2.1 二维载荷计算

由于拉格朗日 -欧拉耦合方法需要耗费庞大的计算资源，在进行层合板响应计算前，首先建立2D空气域模型，进行二维载荷计算，然后导出载荷文件映射到三维模型中，完成整个计算过程。需要注意的是，为了避免实际结构变形引起的载荷分布变化，进而导致映射载荷出现问题，二维载荷计算中的冲击波不能到达壁面，即只能进行前期的TNT起爆过程计算。图10 为二维载荷计算模型，本试验采用端点起爆，在TNT 的左下角设置起爆点（红色标记处）。考虑到试验中的爆炸桶尺寸为180 mm×180 mm×405 mm，因此作为映射载荷的二维模型尺寸选为180 mm×90 mm。为了保证载荷计算的准确性，选取了5 种不同尺寸的网格进行收敛性分析，对比对象为计算域中测点的压力。最终选取的网格尺寸为0.25 mm，模型划分网格总数259 200。

计算中，空气使用理想气体状态方程，TNT 炸药使用JWL 状态方程，具体材料参数[24]如表7 所示。其中： ρC为炸药密度，DC-J为爆速，pC-J为爆轰压力，EC为爆轰能量，A、B、R1、R2、 ω为JWL 状态方程的参数。

对试验中涉及到的装药质量分别进行了载荷计算，如图11 所示，计算中起爆冲击波即将到达边界时停止计算，导出当前计算步的载荷，为三维响应计算提供载荷输入。

图11 二维起爆压力云图Fig. 11 Two-dimensional detonation pressure fringe

2.2.2 三维响应计算模型设置

三维响应计算中，对于空气域和TNT 采用欧拉方法，对于层合板和其他爆炸桶相关结构采用拉格朗日方法。图12 为三维响应计算模型，其中XY平面与层合板平行，Z轴为爆炸桶深度方向，坐标原点在爆炸桶的中心。纤维板的局部坐标系与全局坐标系保持一致，正交编织的纤维方向分别与X轴和Y轴平行。由于层合板响应试验中的爆炸桶壁厚20 mm，在整个试验过程中都没有发生明显变形，因此将爆炸桶内壁视为刚性壁面。同时，爆炸桶的一端开口被同样厚度为20 mm 的钢板密封，也视为刚性壁面。数值模拟计算中用空气域的不可流出边界来模拟刚性壁面，最终整个爆炸桶被简化为层合板内外的两个压板。为了在整个计算过程中保证拉格朗日-欧拉耦合的有效性，空气域在层合板外部的Z轴负方向上延伸了100 mm。二维载荷计算完成后，将计算得到的载荷在三维模型中沿Y轴旋转，完成起爆初始阶段的爆炸载荷输入过程。

图12 整体模型设置Fig. 12 Overall model settings

考虑计算的收敛性与耦合的有效性，最终空气域的网格尺寸选取2 mm，划分网格总数为2 049 300。纤维板、螺栓以及压板使用体网格，铝板使用面网格，这样处理主要是由于试验中使用的铝板厚度仅为0.5 mm，如果要保证网格划分质量，需将层合板平面内的网格划分到与厚度同一个量级，在显式计算中，无疑会大幅度降低稳定计算步长，这将导致在有效时间内无法完成计算，并且对结果可靠性的增益也不明显。最终，纤维板在厚度方向划分为3 个网格，铝板使用面网格，厚度影响区域在中面往两侧各偏移0.25 mm。图13 为A5G43 铺层形式的层合板区域截面剖视图，整体结构的网格总数为112 436。内外压板将层合板夹持以模拟爆炸桶与层合板间的法向接触行为，提供正压力以形成切向滑移时的摩擦力。另一方面，螺栓被简化为限制层合板面内变形的螺杆，螺杆最外围节点数与层合板上螺栓孔内圈的节点数相同，以形成更准确的接触关系。

图13 层合板部位模型剖视图Fig. 13 Sectional view of laminate model

2.2.3 材料参数

对试验所用铝板进行了材料性能测试，图14为铝合金的拉伸工程应力-应变曲线，换算成真实应力-应变后（结果如表8 所示），作为铝板的材料性能输入参数。铝板使用Piecewis-JC本构方程描述，该本构关系是在Johnson-Cook 模型的基础上，将A+Bεnp部分替换为由若干真实应力-应变点连成的折线段，可较好地还原材料本身的属性，并保留原模型对于应变率效应的考虑。本研究中应变率常数取0.05，密度、弹性模量以及泊松比分别取2 690 kg/m3、73.1 GPa 和0.3[28]。

表8 铝合金真实应力-应变输入参数Table 8 True stress-strain parameters of aluminum alloys

图14 铝合金拉伸应力-应变曲线Fig. 14 Stress-strain curve of aluminum alloy

数值模拟中纤维板弹性参数使用上述计算所得参数，以正交各向异性本构方程进行描述。强度参数选取文献[29-30]中提供的热塑性编织玻璃纤维板参数，以材料各方向应力水平作为失效判据，当材料满足失效判据后认为其不再具有承载能力，但不直接移除单元。在前处理中具体的纤维板输入参数如表9 所示。其中：G为剪切模量， σ11、 σ22、σ33为3 个方向的拉伸失效应力，τ12、τ23、 τ31为3 个方向的最大剪切应力。

表9 纤维板材料参数Table 9 Mechanical parameters of fiber reinforced laminate

对于夹持部分，内压板使用刚体属性，由于同一个模型中所有刚体属性结构只能有一种边界情况，因此将外压板与螺栓赋予普通钢铁材料属性，但对于这部分结构的网格，限制6 个方向的自由度，以达到刚体属性的效果。

2.2.4 边界条件

对于空气域部分，在各面上使用不可流出边界，以模拟爆炸桶的刚性内壁；夹持部分涉及到两种边界，对于外压板与螺栓限制6 个方向的自由度，对于内压板施加面压力，这样的组合夹持结构将作为层合板的约束条件，而层合板本身不再设置其他边界，如图15 所示。内压板面压力的取值通过螺栓的预紧力来计算，试验中一共使用16 枚M16 螺栓，对螺栓施加60 N·m 的扭矩，得到每个螺栓上提供的紧固力为18.75 kN，再根据压板面积换算出面压力为5.6 MPa。

图15 夹持部分边界条件施加Fig. 15 Boundary conditions of the clamping part

2.2.5 接触与耦合

接触算法使用Trajectory 算法，采用Penalty 方法进行接触判别。Trajectory 算法与External gap 算法检测结构间隙的处理方法不同。使用Trajectory 算法建模时不需要在所有可能接触结构间预留间隙，而是通过检测结构间的穿透来实现接触。当算法检测到节点间出现穿透时，节点将被拉回到上一个位置，然后通过罚函数计算结构间的接触力。在接触面的切向定义摩擦约束，以模拟夹持结构紧固下层合板在边界处的滑移。同时，由于模型中铝板使用面网格离散，在进行接触计算过程中需按照铝板实际厚度进行接触检测，即Shell thickness 设置为1.0。耦合设置中将空气域与第一层铝板进行耦合，耦合深度为6 mm。

为了模拟铝板与纤维板间的黏接，本研究使用Tie-break 处理方法，将铝板与纤维板对应节点绑定，当应力达到一定值后，节点间的绑定将断开，具体形式如图16 所示。绑定失效参数[30]分别为法向应力达到140 MPa，切向应力达到300 MPa，最大检测距离为0.3 mm。

图16 铝板与纤维板间的绑定Fig. 16 Bonding between the aluminum plate and laminate

2.3 数值模拟结果分析

按照2.2 节的模型设置方法进行数值模拟计算，计算过程涉及复杂的流固耦合和接触判断，初始稳定时间步长在4.8×10-5ms 左右，当层合板在爆炸载荷下发生失效与分层后，计算稳定时间步长在1.7×10-5ms 以下，单个计算文件需要耗时一周左右才能得到层合板的最终稳定变形。

2.3.1 变形对比分析

在背爆面最外层铝板的中心点布置位移测点，待计算结果稳定后，提取最终层合板变形结果，如图17 所示。由图17 可以看出，计算结果与试验最终变形结果吻合较好，所有计算工况误差在10%以内。整体而言，小装药量下计算结果偏小，而大装药量下计算结果稍大，导致这一结果的原因可能有：(1) 夹持板-层合板间的摩擦力大小存在差别，数值模拟中难以模拟真实的试验接触条件；(2) 层合板内的损伤情况与真实试验情况存在一定差别；(3) 数值模拟中没有考虑爆轰产物的燃烧效应，虽然在试验设计过程中已尽量避免了燃烧效应，但试验过程中的真实情况更加复杂，仅依靠装药量与封闭空间体积比来判断燃烧效应不一定完全准确。

观察数值模拟中层合板的最终变形趋势可以发现，在大药量下（20～50 g），变形结果的线性程度较好，即随着药量的增大，层合板最外层铝板的变形线性增大。但同时也可以发现，试验数据与数值模拟结果均在10～20 g 之间存在一个明显的转折点。在试验数据分析中已经提到过这个问题，由于本节数值模拟计算中没有将爆轰产物的燃烧效应计算在内，因此可以进一步肯定该变形趋势上的转折不是由燃烧效应造成的，结合表3 的纤维层损伤情况可以推断，该结果应该与层合板内纤维的损伤情况密切相关，在小药量下，纤维层保存完好，全部材料处于弹性阶段；随着装药量的增大，纤维层中心大变形区域出现纤维的大面积断裂，导致纤维板承载能力迅速降低，层合板表现出变形加快，即在图17 的变形曲线上出现了斜率的增大。

图17 试验与数值模拟最终变形的对比Fig. 17 Comparison of final deformation between test and simulation

2.3.2 夹持边界对变形的影响

试验中夹持边界处的滑移明显，此处的滑移也使得整个响应过程中的非线性程度更大。图18为数值模拟计算中典型层合板整体的变形模式，其中红色标记为初始螺栓孔与受载区域边界的位置，黑色标记为受载区域的塑性铰线与凸起部分。可以看到，夹持边界下，层合板与夹持板间存在相对滑移，但滑移过程中会受到螺栓的约束，使得整体面板在四周出现了波浪形的变形。从整体变形上可以看到，数值模拟结果与试验中的变形模式相同，受载区域对角线上出现明显的铰线，中间大变形区域出现凸起。

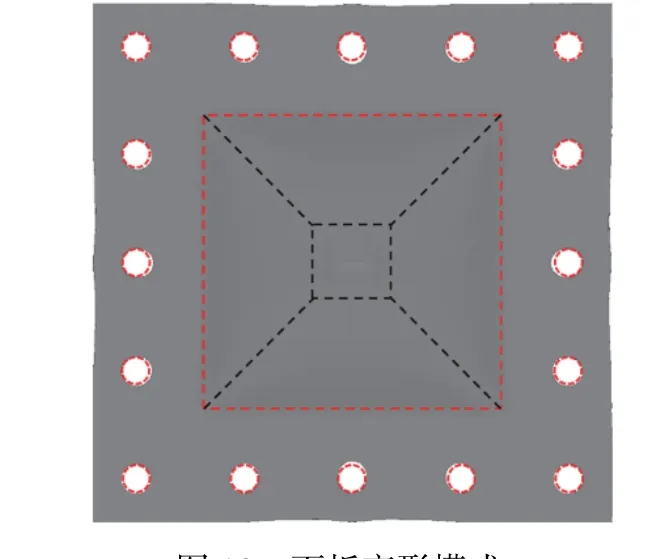
图18 面板变形模式Fig. 18 Deformation mode of the laminate

为了进一步说明夹持边界对结果的影响，同时避免上述由于纤维板失效引起的层合板变形趋势的变化，选取10 g 装药工况进行对比分析。图19 所示为调整边界后的模型，将原有夹持板与螺栓去除，对层合板非受载区域所有节点约束6 个方向自由度。边界条件的简化首先带来的是计算时长的改变，整体计算稳定时长缩短了25%左右。

计算结果对比如表10 所示，可以看到，固支边界下，层合板最终变形明显偏小。按照计算结果进行对比，可以发现固支边界对整体变形的影响达到28.1%，极大地影响最终结果。

表10 夹持边界与固支边界对比Table 10 Comparison of clamping and fixed boundary

2.3.3 纤维板损伤模式

将稳定后最外层纤维板的损伤情况与试验结果进行对比，如图20 所示，其中上方为10～50 g TNT舱内爆炸试验的探伤结果，下方为对应工况下的数值模拟结果。可以发现，就存在的纤维损伤模式而言，数值模拟结果与试验结果吻合较好。但也存在部分小裂纹吻合较差，导致这一结果的主要原因在于网格尺寸的限制。试验结果中存在很多细小损伤裂纹，如果要在数值模拟中重现这一结果，就要求网格尺寸足够精细。而网格尺寸较大会导致原本某处要出现的裂纹，在较大的网格尺寸下，被算法平均到了一个较大范围内，无法满足损伤判据。这一问题直接导致在20 g的装药下，数值模拟无法体现出试验中的细小裂纹，进而导致最终变形计算结果偏小。如果要在模拟计算中体现细小裂纹，计算网格尺寸需要缩小至原模型尺寸的1/10 以上，导致计算时长呈几何倍数增长，数值模拟计算也失去了意义。因此，本研究的计算没有进一步细化。

图20 纤维板损伤模式对比Fig. 20 Damage mode of laminate

对比30～40 g 装药的数值模拟结果与试验结果可以发现，数值模拟中可以将裂纹集中部分体现出来，且形式与试验结果完全一致。但在50 g 装药工况下，试验结果出现了不对称的裂纹形式，这一结果可能与层合板加工过程有关，难以作为有效对比。进一步对比可以发现，计算结果中，失效存在一定的不对称性，这一现象主要是由载荷不对称导致的。而与试验结果中失效不对称相关的因素复杂得多，载荷起爆方式、实际边界约束力的差别、加工过程以及初始损伤情况都会对失效不对称产生影响。

进一步提取层合板截面变形形状进行对比，如图21 所示，其中装药量自上而下逐渐增大。由图21 可以看出，层合板的整体变形模式与试验结果的吻合度很高，大药量下的分层主要集中在夹持端部与中心位置。需要说明的是，试验中纤维断裂后扫描结果将不再体现，而数值模拟中为了对比不同的失效模式，纤维层失效后仅失去承载能力，单元仍被保留。将图20 中的纤维失效范围代入层合板截面对应位置，可以看到，数值模拟较好地重现了这一过程。

图21 层合板截面变形与分层Fig. 21 Deformation and delamination of laminate(sectional view)

进一步对分层过程进行研究，图22 展示了典型层合板响应过程中的截面变化情况。可以发现，夹持层合板首先受到壁面上传来的初始冲击波作用，在边界处出现明显变形，逐渐向中心部位聚拢，最终形成盘状的大变形模式。随后，层合板结构达到饱和响应，冲击波载荷不再使层合板变形继续增大，层合板开始回弹。在回弹过程中，层合板不同层之间通过黏结力维持整体运动，但不同层间由于变形量与损伤程度的不同，回弹的回复力也不一样，这个过程中就出现了分层现象。这一过程与试验中层合板最终表现出的变形模式一致。

图22 典型层合板响应过程Fig. 22 Typical laminate response process

3 结 论

基于开展的舱内爆炸载荷作用下层合板的动态响应试验，开展了层合板数值模拟研究，得到以下主要结论：

(1) 舱内爆炸载荷作用下，整体层合板在未出现明显外部破坏的情况下，内部纤维层合板中已出现大面积纤维断裂与分层，该破坏过程能够吸收爆炸载荷能量，使层合板的抗冲击能力增强；

(2) 针对试验过程开展了对应的数值模拟研究，数值模拟结果与试验结果的变形误差在10%以内，且与试验现象吻合较好，同时发现，试验所用夹持边界对层合板的变形影响较大，在对比计算中，固支边界对整体变形的影响达到28.1%；

(3) 对比燃烧效应不显著的试验结果与数值模拟结果，可以发现纤维层中的纤维断裂与层合板响应趋势的改变密切相关，纤维层的破坏将明显降低层合板的承载能力。