山东近海底层鱼类资源空间异质性
吴桢,张崇良, ,薛莹, ,纪毓鹏,,任一平,,徐宾铎,*
(1.中国海洋大学 水产学院,山东 青岛 266003;2.青岛海洋科学与技术试点国家实验室 海洋渔业科学与食物产出过程功能实验室,山东 青岛 266237;3.海州湾渔业生态系统教育部野外科学观测研究站,山东 青岛 266003)
1 引言
生物种群在空间上并不是随机分布的,而是呈现特定的空间分布格局,鱼类种群也不例外。了解鱼类种群的空间分布格局是重要的生态学研究,也是对具有商业价值以及保护价值的鱼种进行管理的必要条件[1]。空间异质性是指系统在空间上的复杂性和变异性,是生态学过程在不同时空尺度上作用的体现,是产生空间格局的主要原因[2]。自1950 年以来,由于捕捞力量增加,山东近海渔业资源从利用不足到充分利用、过度利用,其中底层鱼类资源衰退严重[3]。许多底层鱼类是重要经济鱼种,这些经济鱼种的数量和生物量波动会对渔业捕捞的经济效益产生较大影响。同时,底层鱼类种类众多,在山东近海鱼类群落中占据较高比例,发挥着重要功能,在山东近海渔业资源中占据重要地位[3-4]。
地统计学是研究自然现象空间变异与空间结构的一门学科[5]。基于生态系统的渔业管理需要处理空间问题,渔业活动管理以及生境保护等需要了解精确的资源分布。地统计学提供了一系列解决方案,可以用于绘制和描述空间分布的不同方面,也有助于模拟生境和了解空间分布[6]。地统计学在生态学上的应用包括变异函数图像、克里金插值等[7],如Platt 和Denman[8]将近似于变异函数的频谱分析应用于生态学案例。地统计学方法在渔业领域也应用较广[9]。如Sullivan[10]应用地统计学方法对黄线狭鳕(Theragra chalcogramma)声学数据进行处理,确定了鱼类密度的空间均值和方差、总丰度及其方差;Simard 等[11]研究了圣劳伦斯湾小型中上层鱼类的空间结构、影响因素和干扰因素;苏奋振等[12-13]运用空间自相关指数和变异函数分别分析了东海中上层鱼类和底层及近底层鱼类的空间结构;张寒野和程家骅[14]利用变异函数分析了东海小黄鱼的空间异质性并进行了插值;杨铭霞[15]使用了地统计学方法对西太平洋柔鱼资源的空间变异进行了分析。
本文利用空间自相关指数和变异函数对山东近海底层鱼类的空间相关性和空间异质性进行研究,了解底层鱼类在不同季节下空间格局的变化,探寻环境因素与空间结构之间的关系,以期为山东近海渔业资源可持续利用和管理提供参考依据。
2 材料与方法
2.1 数据来源
本文数据来源于2016-2017 年山东近海渔业资源底拖网调查。调查海域范围为35°00′~38°30′N,117°30′~124°30′E,调查于秋季(2016 年10 月)、冬季(2016 年12 月至2017 年1 月)、春季(2017 年5 月)、夏季(2017 年8 月)进行,共4 个航次,以格状均匀定点法设计调查站位,共设置177 个站位。由于天气、地形和养殖区等原因,部分预设站位在实际调查中未能完成,其中春季共调查158 站,夏季共调查156 站,秋季共调查159 站,冬季共调查163 站。调查及分析按《海洋调查规范 第6 部分:海洋生物调查》(GB 12763.6-2007)[16]和《海洋渔业资源调查规范》(SC/T 9403-2012)[17]要求进行。采用功率为220 kW 的单拖底拖网渔船作为调查船,调查网具网口高为7.53 m,网口宽为15 m,网囊网目为17 mm。拖网调查均安排在白天进行,设计每站拖网时间为1 h,拖速为3.0 kn,但实际调查存在变化。本文选取所有底层鱼类,将各站位的渔获量数据换算为拖速3.0 kn、拖网时间1 h的每网每小时拖网渔获量,即相对资源量指数(单位为kg/(网·h))。
2.2 正态性检验
使用地统计学方法进行空间统计分析的前提是数据满足正态分布。本研究对2016-2017 年底层鱼类的相对资源量指数数据进行了单样本Kolmogorov-Smirnov 检验,若其不满足正态分布,则对其进行对数正态化转换,以满足地统计学的分析要求[15-18]。
2.3 空间趋势性分析
地统计学空间数据趋势特征表现在其能够量化和描述空间区域中地理现象的变化程度和方向变异性[19]。趋势分析可以反映对象在空间区域内变化的主体特征,其揭示研究对象的总体规律,而忽略局部的变异。全局趋势图中的X轴代表正东方向,Y轴代表正北方向,垂直方向的矢量棒代表各个站位的相对资源量指数,数据点投影至东西向和南北向的平面上形成趋势线。
2.4 空间相关性分析
空间自相关用于度量空间对象及其相应的某一属性值在空间上的聚集程度。空间自相关分为全局自相关和局部自相关,全局自相关描述整体分布情况,判断某属性在特定区域内是否有聚集特征存在;局部自相关能指出显著的聚集发生在哪些位置[20-24]。
2.4.1 全局空间自相关
(1)全局莫兰指数(Global Moran’sI,以下简称I)为研究渔业生物资源的聚集、离散或随机空间分布模式,采用探测性数据分析方法中的全局空间自相关统计量I进行度量[20-21]。公式为

式中,n为样本数量;xi为i点的相对资源量指数;xj为j点的相对资源量指数;为样本平均值;wi,j为i点和j点之间的空间权重;S0为所有空间权重的聚合。
I的值大于0 表示正相关,小于0 表示负相关。I绝对值越大,表示空间分布的自相关性越高,即空间分布的聚集性越强;I绝对值越小代表空间分布的自相关性越低,说明空间分布呈现分散格局;当I值等于0 时,表示空间分布呈现随机分布。在计算中,I会返回另外两个值:Z得分和p值。其中,Z得分是标准差的倍数,当Z较大时,表示渔业资源呈聚集分布状态。p值表示样本空间模式随机分布的概率,p值小于0.01 表示渔业资源是随机分布的概率较小。
(2)Getis-Ord GeneralG(以下简称G)与I类似,全局空间自相关统计量G表示可度量高值或低值的聚类程度[21-24]。公式为

G值的范围为0~1。G的0 假设规定不存在样本的空间聚类,若p值较小且在统计学上显著,则可以拒绝0 假设。此时,当Z值为正数时,G的观测值比期望值大,表明相对资源量指数高值在研究区域内聚类;当Z值为负数时,G的观测值比期望值小,表明相对资源量指数低值在研究区域内聚类。
2.4.2 局部空间自相关
为分析渔业资源在局部空间内的分布特征,本文采用Getis-Ord指数(以下简称)判别具有统计显著性的高值(热点)和低值(冷点)的空间聚类[21-24]。热点为高值区聚集,冷点为低值区聚集。公式为
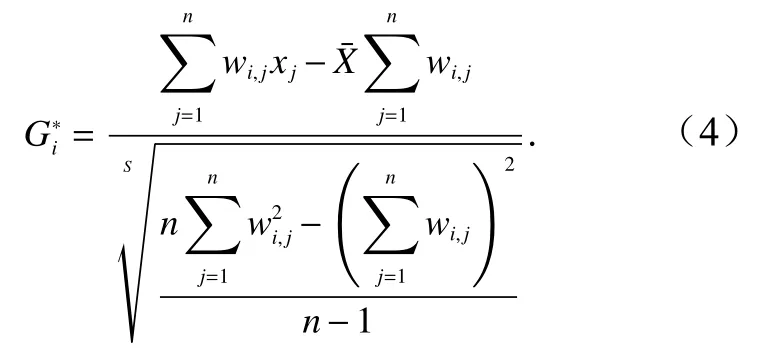
2.5 空间异质性分析
本文采用变异函数来定量描述底层鱼类在山东近海的空间变异情况,假定其服从二阶平稳假设。变异函数公式为[25-26]

式中,h为步长;N(h)是距离等于h时的点对数;Z(xi)是区域化变量Z(x)在空间位置xi的上的观测值。
区域化变量Z(x)所具有的空间异质性可分为随机变异和空间自相关变异这两部分,可利用模型拟合后所得的参数进行定量分析[27]。在各项同性的前提下,对半变异函数进行模型拟合。常用的变异函数拟合模型有3 种,分别是球状模型、指数模型和高斯模型[25-26]。各模型公式为
(1)球状模型

式中,r为滞后距离;C0为块金常数;C0+C为基台值;C为拱高;a为变程。
(2)指数模型

式中,a为1/3 变程。
(3)高斯模型

式中,a为变程。
其中,指数模型表示变量相关性距离较大,聚集程度相对较弱;高斯模型表示个体在中间特定区间空间相关性大,而前后阶段都较弱;球状模型表示个体间的聚集性较强,空间相关距离较小[27]。模型参数基台值C0+C表示总的空间异质性程度,块金值C0表示随机部分的空间异质性,拱高C表示空间自相关部分的空间异质性。本文使用残差平方和(Residual Sum of Squares,RSS)和赤池信息准则(Akaike Information Criterion,AIC)检验模型拟合优度[28]。
3 结果
3.1 常规描述性统计
山东近海底层鱼类春季相对资源量指数变化范围为0.030~140.37 kg/(网·h),平均值为9.16 kg/(网·h);夏季相对资源量指数范围为0~272.54 kg/(网·h),平均值为25.43 kg/(网·h);秋季相对资源量指数范围为0~634.38 kg/(网·h),平均值为36.66 kg/(网·h);冬季相对资源量指数范围为0.028~78.11 kg/(网·h),平均值为7.82 kg/(网·h)。变异系数大于100%时,数据离散程度大,4 个季节底层鱼类分布差异性均较大。从数据的整体趋势上来看,秋季的相对资源量指数最高,变异系数较大,数据离散性程度较高,春、冬季的相对资源量指数较低,春、夏、冬季的变异系数相近,数据离散性程度相对于秋季较低。4 个季节的偏度均大于0,频度分布为正偏,峰度均大于3,呈高狭峰,表明山东近海底层鱼类分布以低相对资源量指数区为主。K-S检验所得p值均小于0.05,数据不符合正态分布,后续进行对数正态转换(表1)。

表1 山东近海底层鱼类相对资源量指数描述性统计分析Table 1 Descriptive statistical analysis of relative abundance index of demersal fish in the offshore waters of Shandong
3.2 空间趋势分析
山东近海底层鱼类相对资源量指数在春季明显表现出南高北低的趋势,在东西方向上,东部相对资源量指数略高于西部。在夏季和冬季,底层鱼类相对资源量指数在东西方向上明显表现出东高西低的趋势,而南高北低的趋势略微减缓。在秋季,底层鱼类相对资源量指数在东西方向表现出东高西低的趋势,在南北方向上的趋势表现不明显(图1)。

图1 山东近海底层鱼类相对资源量指数全局趋势Fig.1 Global trend of relative abundance index of demersal fish in the offshore waters of Shandong
3.3 空间自相关性分析
3.3.1 全局空间自相关
4 个季节的I观测值均大于0,山东近海底层鱼类存在空间自相关性,且为正相关,p值小于0.01,Z得分较高,底层鱼类在山东近海呈现显著的聚集分布格局。4 个季节的G观测值均大于预测值,Z得分为正值,表明山东近海底层鱼类在高相对资源量指数区域的聚集性较强。从整体趋势上来看,I和G在春季、夏季和冬季的Z得分较高,在秋季的Z得分较低,表明底层鱼类在春季、夏季和冬季的空间聚集程度强于秋季(表2)。

表2 山东近海底层鱼类全局空间自相关指标Table 2 Global spatial autocorrelation indexes of demersal fish in the offshore waters of Shandong
3.3.2 局部空间自相关
4 个季节中热点通常分布于山东半岛南部海域,冷点通常分布于山东半岛北部海域。在春季和夏季,热点分布在海州湾近岸海域且热点数量较多;秋季热点向外海迁移并且数量减少;冬季热点从山东半岛南部的外海移向近海,同时热点在蓬莱近海附近也有小范围聚集。冷点四季均分布在莱州湾及邻近海域,秋季有自西向东迁移的趋势(图2)。

图2 山东近海底层鱼类冷热点分析Fig.2 The hot spots and cold spots analysis of demersal fish in the offshore waters of Shandong
3.4 空间异质性分析
从模型拟合结果来看,春季、夏季和秋季3 个季节拟合效果最好的模型均为高斯模型,反映了底层鱼类在达到一段特定间隔距离h时的自相关性较强,特定间隔距离h前后自相关性较弱;冬季拟合效果最好的模型是球状模型,反映了底层鱼类个体间的聚集性较强。秋季的块金系数最高,夏季、春季其次,冬季的块金系数最低。从块金系数可知,秋季具有较强的块金效应,随机部分的空间异质性占总空间异质性的75.95%,而春季、夏季和冬季的块金效应较弱,随机部分的空间异质性仅占总空间异质性的26.15%、27.68%和23.64%,空间自相关性部分占主导地位。春季、夏季和冬季的变程较大,秋季的变程较小,表明山东近海底层鱼类的空间自相关距离在春季、夏季和冬季较大,底层鱼类相对资源量指数在较广的范围内呈现空间结构化分布(表3)。

表3 山东近海底层鱼类变异函数模型各项参数Table 3 Parameters of semi-variogram for demersal fish in the offshore waters of Shandong
4 讨论
本研究表明,山东近海底层鱼类具有显著的空间聚集格局,秋季的空间自相关性较弱,其他季节空间自相关性较强。底层鱼类体现了明显的空间分布格局,相对资源量指数高值聚集区(热点)在春季、夏季位于山东半岛南部海域,在秋季、冬季高值聚集区的范围大幅减小,而低值聚集区(冷点)四季均集中在莱州湾海域(图2)。秋季高值聚集区范围变化的可能原因包括:(1)秋季底层鱼类多处于索饵洄游阶段,其分布较其他季节更为分散;(2)经过伏季休渔,秋季相对资源量指数增加,底层鱼类向外海洄游而超出调查海域范围,使得高值聚集区的范围减小,进而造成了秋季的变程较小,即底层鱼类在秋季的空间自相关距离较小。夏季高值聚集区聚集鱼种主要是暖温种小眼绿鳍鱼(Chelidonichthys spinosus),冬季高值聚集区聚集鱼种主要是黄鮟鱇(Lophius litulon)和细纹狮子鱼(Liparis tanakae)。鱼类群落的空间分布是环境因子相互作用的结果,并不受单一因子的控制,其中水温的影响最大,底层鱼类向外海深水区洄游的主要原因为适温洄游[29-30]。水温受海流影响,山东近海南部近岸海域风生流场存在上升与下沉现象[31],致使夏季的海水底温升高,此外,冬季黄海暖流的分支流经海域也能使得部分暖温种季节性地在近海聚集[29-30],这与海州湾各适温型鱼类的空间分布研究结果一致[32],说明水温是影响山东近海底层鱼类空间自相关性和空间异质性的重要因素。图2 相对资源量指数高值聚集区的季节变动体现了优势种类在四季的洄游变迁,小眼绿鳍鱼是山东近海南部海域的优势种之一,4-5 月在近岸海域产卵,秋、冬季则洄游至水深更深的海域[33],符合图2 热点的变动。而山东近海优势种之一的细纹狮子鱼,同样为季节性产卵,产卵时期主要集中在春、夏季[34],符合图2 热点的分布,可见春、夏季相对资源量指数高值区多与优势群体的产卵时期分布有关。
从变异函数拟合结果来看,秋季拥有最大的块金常数和块金系数以及最小的变程。本研究中块金常数和相对资源量指数存在着正相关关系,说明随机变异在年间相对资源量指数的变化中有一定程度上的体现,这与东海底层鱼类空间异质性研究结果相近[13],同时块金系数和变异系数也基本呈正相关关系。块金常数表示由实验误差或小于实验取样尺度引起的变异,较大的块金常数说明在该尺度下存在着重要的生态学行为[14,26]。因此,在进行山东近海渔业资源调查时,应适当扩大调查范围和站位数以使获得的数据更有代表性。从季节变化上来看,秋季的块金系数较其他季节更大,表明秋季的随机变异在底层鱼类的空间异质性中占了很大的比重。而春季、夏季和冬季的块金系数均接近25%,空间异质性中结构性成分所占比重较大,底层鱼类相对资源量指数在空间上呈现结构化的范围较广。
通常运用变异函数分析空间异质性时会以各向异性为前提进行分析,判别不同方向上的各项参数,从而得到不同方向上随机性和结构性在空间异质性中所占比例[12-18]。本文拟合变异函数时所采用的是各向同性前提,原因是受数据点的数量限制,若以各向异性为前提,各方向的数据量过少,不足以支持结论的有效性。除此以外,本研究中基台值与相对资源量指数并不完全呈正相关关系,这与其他研究的结果有所差异[13-14,27],造成这种情况可能是底层鱼类相对资源量指数在秋季时的拱高过小,且不同步长h下相对资源量指数的差值过小所导致的,即秋季底层鱼类资源分布较为均匀。本研究结果表明,山东近海底层鱼类的空间自相关性和空间异质性存在着显著的季节变化,这与环境因子的变动尤其是水温的变化有直接关系。为了更好地阐明环境因子与底层鱼类空间自相关性及空间异质性之间的关系,应在后续的研究加入环境因子的相关性分析。

