新型连续梯度变截面薄壁圆管耐撞性多目标优化设计
熊 锋, 付 杰, 石晓辉,曾四海
(重庆理工大学 车辆工程学院, 重庆 400054)
基于薄壁结构在碰撞过程中能通过自身变形吸能以保护乘员安全方面的优越性,大量学者对于薄壁梁结构耐撞性能进行了大量的解析、实验以及数值模拟的研究分析。总的来说,薄壁结构的吸能特性主要受其结构参数的影响。为探寻出薄壁结构的最优结构参数,对不同截面形状和变直径的薄壁结构进行了研究。其中,由于能形成稳定的溃缩形式,圆管受到了广泛关注研究[1-2]。Alexander[3]在1960年率先对圆形薄壁管的轴向压溃特性进行探究。Zhang等[4]对多种不同截面形状圆形薄壁管的变形模式和吸能特性进行了准静态压缩试验研究。曾杰[5]对径向冲击载荷下不同参数的金属管的变形和吸能进行了研究。黄睿等[6]对圆管的吸能特性进行了参数分析,包括高度、壁厚、直径以及泡沫铝的填充的影响。常亚飞[7]对径向和轴向准静态荷载以及冲击碰撞作用下圆管的变形模式和吸能特性等进行了研究。圆锥管由于在受到动态冲击时变形模式稳定,峰值力更小,也被广泛研究[8]。徐龙江等[9]在轴向冲击载荷作用下分别对薄壁金属圆管和变径管两种结构进行数值模拟,发现变径管变形模式稳定,载荷-位移曲线平稳。
根据当前各种薄壁结构研究现状的总结,目前,对于圆锥管的研究很少有学术报道研究直径呈函数梯度非线性变化的结构形式。基于以上研究背景,本研究提出一种函数梯度圆锥管(FGTT),对其耐撞性能进行分析并对薄壁结构进行多目标优化设计。FGTT的直径沿着其轴向以一种函数梯度的方式变化。首先,利用HYPERMESH和非线性有限元软件LS-DYNA建立圆锥管的数值模型,通过实验数据验证其有效性。其次,对比了线性圆锥管和非线性FGTT管的耐撞性,FGTT管在不同n值、不同压溃距离和不同压溃速度下的初始碰撞峰值力和比能量吸收等耐撞性能指标。最后,采用响应面法(RSM)来近似模拟FGTT管关于非线性梯度的耐撞性目标函数,为了达到比吸能(SEA)最大和初始峰值力(IPCF)最小的目的,建立了多目标优化模型,并采用在耐撞性设计中非常有效的非支配序列遗传算法(NSGA-Ⅱ)完成了多目标优化设计。
1 几何特征和材料描述
1.1 几何描述
如图1所示,FGGT管是一种直径沿轴向变化而壁厚保持不变的锥型管。该结构的直径变化与SUN G等提出的薄壁结构厚度以函数梯度变化类似,FGTT管直径沿轴向的变化可用一个指数函数来描述[10]:
(1)
其中:Rt和Rb表示FGTT管的上下端半径;x是到顶端的轴向距离;L是薄壁管的轴向总长度;n是用来改变半径数值大小的梯度指数,该指数变化区间为[0.1,10]。
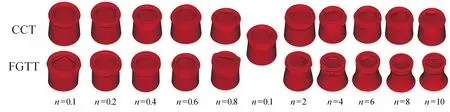
根据式(1)可知,当n在0.1到10变化时,如图2所示FGTT管外形逐渐从外凸变为内凹。取不同n值时,FGTT管外形见图3。

图2 FGTT管半径与指数n的变化关系曲线

图3 不同n时FGTT管几何外形示意图
1.2 材料属性
FGTT管制造材料为钢,具体参数参照Ahmad[11]等的试验结果。具体参数:屈服强度σy=401.4 MPa,弹性模量E=200 GPa,泊松比v=0.3,密度ρ0=7 809 kg/m3。有限元模型采用图4中的材料应力应变曲线。

图4 塑性应力-应变曲线
2 有限元模型验证
2.1 有限元模型建立
本文中所有进行轴向动态冲击仿真的FGTT管均由LS-DYNA软件完成有限元建模,对应边界条件和载荷见图5,管件的底部节点被为600 kg的刚性墙以15 m/s的初始速度进行撞击[12]。薄壁管采用在厚度方向定义5个积分点的4节点的Belytschko-Tsay薄壳单元模拟[13]。有限元模型中采用的是分段线塑性MAT24材料作为仿真材料本构。为防止管件压溃时发生自身穿透,采用“automatic single surface”接触类型,接触参数动摩擦因数为0.2,静摩擦因数为0.3[14]。此外,为了既满足精度要求,又有合适的计算效率,有限元模型的网格大小定为1 mm×1 mm。

图5 FGTT有限元模型
2.2 模型验证
根据式(1)可知,当梯度指数n=1时,FGTT管的几何构型呈圆锥管,可视为FGTT管的一种特殊模式且考虑到梯锥形管的制造工艺问题,本文中的FGTT管均使用圆锥管进行有限元模型有效性验证。采用的圆锥管的具体尺寸如下:高为 150 mm,上下直径分别为40 mm和60 mm,厚度取1.4 mm。图6为实验和仿真的力-位移曲线,可以看出,仿真和实验曲线与实验结果较好地吻合[11]。

图6 仿真与实验力-位移曲线对比
3 FGTT管耐撞性能分析
3.1 等质量FGTT 管与圆锥管(CCT)耐撞性对比
取FGTT管上下端直径分别为40 mm和60 mm,壁厚2 mm。如式(2)所示,当n=1时,FGTT管的半径呈线性变化;当n≠1时,FGTT管的半径将发生非线性变化。易知线性变化FGTT管即为圆锥管(circular conical tube,CCT),为了比较FGTT管与圆锥管耐撞性能好坏,对CCT管与非线性FGTT管进行耐撞性能分析。FGTT管的质量计算公式[12]如下:
(2)
对于CCT管,n值为1,因此易得CCT和FGTT管在同质量下的厚度关系为:
(3)
式中,tC和tF分别为CCT和FGTT管壁厚。
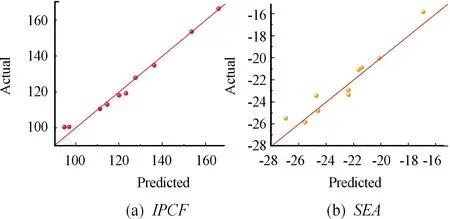
图7所示为不同n值下NLFGTT与CCT的初始峰值力(IPCF)和比吸能(SEA)的相对差值(relative difference,RD)。当n从小于1变化到大于1时,IPCF和SEA的相对差值RD也从负值变化为正值。IPCF的负值RD表示NLFGTT管的IPCF比CCT管的更低;同理,SEA的RD负值表示NLFGTT管的SEA CCT管更低。IPCF值越小,结构受冲击时人体受到的冲击损伤越低;SEA值越大,结构的单位质量能量吸收越高。当0.1 图7 非线性FGTT管 与对应CCT管SEA和IPCF相对差值 综上,相对变直径功能梯度锥形管FGTT而言,在耐撞吸能方面,圆锥管CCT并不是最好的一种薄壁吸能元件。相同质量下,FGTT结构与对应CCT结构压溃变形过程如图8所示。 图8 NLFGTT管与对应CCT管压溃变形过程图 3.2 上下直径差ΔD和不同梯度指数n对FGTT管耐撞性能影响 FGTT的外形轮廓主要由梯度指数n、上端直径Dt和下端直径Db决定。在本节中,对上下直径差ΔD=Db-Dt和指数n进行参数分析,进而了解这些参数对FGTT的耐撞性能的影响。对于所有的FGTT,下端直径不变,为80 mm,上端直径则设置为40~60 mm,变化梯度为5 mm,相应的直径差ΔD为40 mm、35 mm、30 mm、25 mm和20 mm。图9为当取不同上端直径Dt和n时的FGTT的吸能特性。可以看出,在小角度碰撞下,随着n的增加SEA值也相应地增加。对于20°<θ<30°,随着指数n从1变化到10,SEA值随之减小。此外,随着ΔD在区间[20,40]变化时,SEA的值也会产生变化。当碰撞角度较小时(0°和10°),SEA值在n>1时随ΔD的减小而减小,且在n<1时,不同ΔD的SEA值相差并不大。对于大角度碰撞,如20°和30°,在n>1时SEA 值随着ΔD的增大而减小,且较小ΔD的FGTT似乎具有更大的SEA值。因此,不同ΔD和n值所对应的FGTT管可为不同条件下的耐撞性要求提供指导和参考意义。 在真实的碰撞情况下,进行碰撞吸能的薄壁结构经受的碰撞速度并不相同,其吸能特性也会变化,因此有必要探究FGTT在不同碰撞速度下的吸能特性,将初始碰撞速度v分别设定为5、15和25 m/s,分别代表发生碰撞时的低、中、高速3种碰撞情况。 不同碰撞速度下的FGTT吸能特性见图10。由图中信息可知:随着速度从5 m/s增加到25 m/s时,MPCF值也随之增加,但SEA值反而减小,但15 m/s和25 m/s相差不大且受n值影响较小。 图9 不同上端直径Dt和n时的FGTT管SEA值 图10 不同碰撞速度下FGTT管吸能特性 由上节的仿真分析可知:在轴向压溃载荷下FGTT管的吸能指标受到结构参数的影响。本章以梯度指数n、壁厚t、截面尺寸Rt为设计变量,选取最小化峰值力IPCF和最大化比吸能SEA为优化目标,进行FGTT薄壁管在轴向压溃载荷下的多目标优化设计,以获得最优的结构参数匹配,使其呈现更好的吸能表现,多目标优化流程如图11所示。 图11 FGTT管多目标优化流程图 FGTT管的单位质量的吸能量越大,即比吸能SAE越大,证明其吸能特性越好。而从乘员安全角度考虑,较大的初始峰值力IPCF将造成较大冲击和伤害。因此,将SEA和IPCF作为优化目标函数,此时优化问题可描述为: (4) 式中,n为梯度指数,ΔD是上下端直径差值,t是管壁厚度。 采用软件ISIGHT下的DOE模块,以梯度指数n、壁厚t、截面尺寸Rt为实验变量,以梯度指数n=5 mm,壁厚t=2 mm,上端半径20 mm为基础,以此基础的70%~130%作为变量取值范围;采样方法采用最优拉丁超立方(optimal latin hypercube,OLH)得到60组梯度指数n、壁厚t、截面尺寸Rt的变量值;以每组的变量值建立FGTT有限元模型,得到60组IPCF和、SEA响应值。限于篇幅,列举部分结果见表1。 响应面法(RSM)已被证明特别有效,并在耐撞性设计中被广泛采用[15]。为构建响应面近似模型,由于本次优化问题中有3个变量,采取二阶多项式响应面模型并选取10个样本点完成模型精度验证。根据验证结果,在该近似模型中IPCF和SAE的复相关系数R2值均大于0.9。由图12可知,近似模型模拟精度较好,可代替仿真模型用于后续多目标优化。 表1 试验设计结果 图12 代理模型模拟精度 采用第二代非支配遗传算法(NSGA-Ⅱ)完成多目标优化,优化后的Pareto解集如图13所示。将优化结果代入有限元模型进行计算,多目标优化结果、有限元仿真结果及相对误差Re如表2所示。 图13 多目标优化设计结果 表2 优化解与仿真值对比 表3给出了多目标优化后的结构与初始设计结构耐撞性能指标对比,原结构与优化结构几何构型和压溃变形对比如图14所示。可知,经优化后的FGTT结构与初始常规圆锥形结构相比,其初始峰值力得到了很大程度的改善,下降了45.4%;比吸能也较原结构提高了13.5;同时,与原结构相比该FGTT结构的质量减少了51.031%。由上述分析可知,优化结构不仅改善了耐撞性能,同时还达到了轻量化的效果,证实了本次优化设计工作的有效性。 表3 初始值与仿真值对比 图14 优化变形结果对比 针对变直径梯度锥形管研究较少的情况,利用试验验证的铝合金薄壁管材料参数,验证了有限元模型的有效性,并通过仿真模型对比分析了FGTT管和对应锥形管以及不同载荷参数时在动态冲击载荷条件下的吸能特性。仿真结果表明:在所研究的各类薄壁管中,FGTT薄壁管的比吸能和载荷力在特定条件下体现出了较好的吸能特性。在FGTT管长度和下端直径保持不变的情况下,以厚度t、梯度指数n和上端半径Rt作为设计变量,比吸能与初始碰撞峰值载荷为响应,采用响应面近似模型与第二代非支配遗传算法(NSGA-Ⅱ)相结合的方法进行多目标优化。经优化求解,并对数值解和有限元模型分析结果进行对比,表明了该优化模型及结果的有效性。
3.3 不同碰撞速度对FGTT管耐撞性能影响


4 FGTT管的多目标优化
4.1 FGTT管多目标优化流程

4.2 优化问题描述
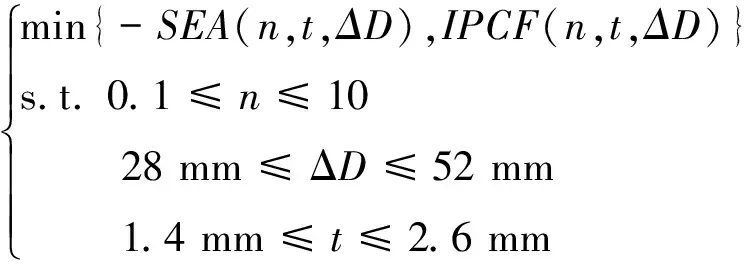
4.3 试验设计
4.4 RSM近似模型

4.5 多目标优化结果及验证




5 结论

