基于破坏力学轴承寿命模型综述

张 珂，李青松

(上海应用技术大学 机械工程学院， 上海 201418)

轴承作为机械运转的关键性部件运用于工程领域，其中滚动轴承因具备摩擦系数小、精度高、互换性好、无需繁琐供油润滑等系列优点得到广泛应用[1]。轴承作为机械设备高速运转的重要部件，其运行状况直接影响主要设备正常工作[2]。研究中表明：在高速回转机构中因轴承故障失效引起的设备损坏占机械故障损坏的30%，轴承失效磨损损坏已成为设备修理和主机损坏的主要问题[2-3]。因此，轴承寿命的可靠性备受关注。

随着科学技术的进一步发展，在技术允许条件下可以对轴承的疲劳寿命和疲劳磨损进行更为深入的研究。本文主要针对轴承寿命理论、疲劳寿命断裂力学和损伤力学预测模型研究工作进行综述分析，并总结性地提出寿命分析研究新思路和未来轴承行业寿命分析发展趋向。

1 国内外轴承寿命研究现状

轴承运转过程出现的故障和损坏必然影响设备工作；轴承寿命概念可用于解释轴承疲劳现象[4-5]。轴承的寿命与设备安全息息相关，如图1所示。

国外机械技术人员对滚动轴承疲劳寿命十分关注。当轴承承载超负荷时，其疲劳寿命、可靠性将不再满足设计要求，构建分析模型是对轴承寿命分析较为有效的方法。1924年，J.V.帕姆格伦以假设轴承累积损伤与转数n的线性关系为条件预估轴承寿命；1945年，M.A.迈因纳总结性地提出轴承疲劳寿命线性损伤累积理论；Tong等[6]建立了一个新的数学模型，通过比较多个加载条件来系统地评价角错对齐对锥形滚子轴承疲劳寿命的影响；Simons等[7]阐述了影响轴承数量、润滑脂桶和故障与维修期间使用的工时数量之间有很强的正相关关系，并分析了旋转轴错位对轴承寿命的影响；König等[8]建立了的轴承寿命模型可确定混合动力轴承的优劣处并分析轴承寿命；Guillermo等[9]在高速、速度、负载和不利的环境下基于蠕变机制的新表面损伤积分来探索接触中的温度摩擦功能造成的损害，为实现疲劳寿命预测可行性；Warda等[10]考虑轴承径向游隙和滚子轮廓并确定疲劳应力分布的圆柱滚子轴承寿命分析方法来研究轴承疲劳寿命。

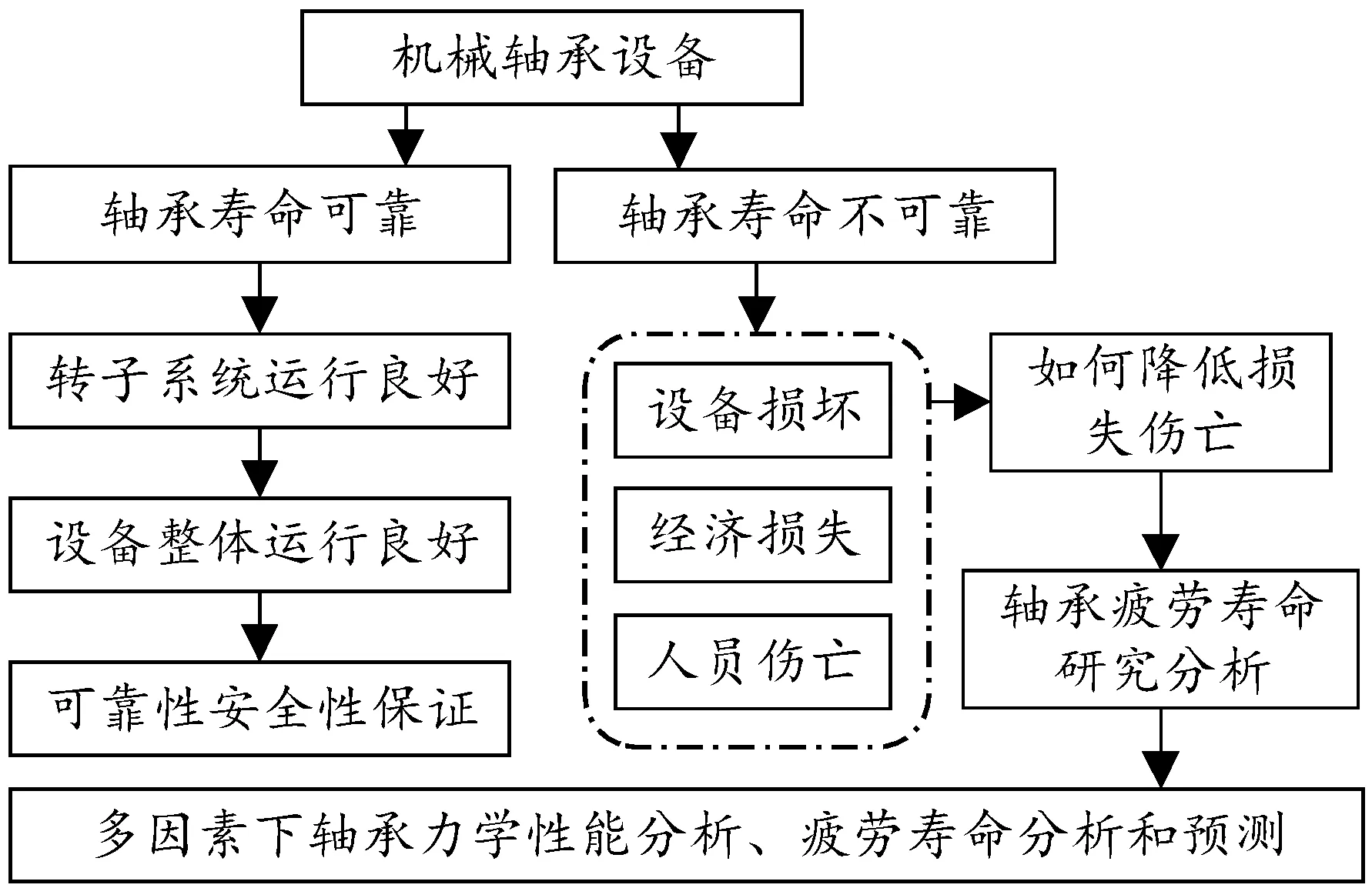
图1 轴承寿命与机械设备关系框图

国内科学技术的发展对超高精、高速、低噪、高载、长寿命、高可靠、高稳定性的轴承需求激增[11]。性能优异的轴承产品建立在成熟设计技术、高性能材料制造研发技术、良好的润滑技术、优异的密封技术的基础上[12]，研究人员即以此为基础对轴承寿命进行了大量的研究。郑光泽等[13]通过修正齿轮参数、齿轮位置的合理布置在Masta软件建立转子系统仿真分析模型来有效延长轴承寿命以及可靠性；Zhang等[14]提出了一种动态磨损仿真模型来探讨在不同预装方法及磨损对轴承磨损寿命和预载量变化的基础上来预测轴承寿命；宋宏智[15]提出基于物理和数据驱动的轴承剩余寿命预测方法，通过实时数据实现精准轴承寿命预测；雷刚等[16]运用有限元分析轴承套圈与不同窜辊量状态下的偏载接触状态得到接触应力分布的偏载效应规律，为轴承寿命分析提供依据；王国辉[17]利用ANSYS、ADAMS构建软件分析模型进行仿真和寿命预测并提出一种静力学、动力学相结合的方法来分析重卡轮毂轴承力学模型及侧向加速度的影响；Yin等[18]提出了一种基于有效数据集来对轴承性能评定的瓦瑟斯坦距离和累计总和的轴承健康评估新指标来以此评估预测轴承剩余使用寿命；袁腾飞[19]从结构、寿命出发在三代轮毂轴承基础上考虑游隙和交变应力并提出轴承结构改进方法来减小轴承受载不均以提高轴承寿命；Zhang等[20]基于最大估算法计算轴承实际值，利用曲线估计和灰色模型预测轴承寿命，并对两种模型对比优劣；蒋旭君[21]运用轴承静平衡方程提出实况下滚子、滚道接触状态载荷分布计算模型，分析游隙与滚子接触载荷大小及分布对疲劳寿命的影响。

目前，轴承寿命问题研究的不足和趋势为：

1) 基于传统接触探讨理论计算接触载荷、应力、弹性趋势等问题，理论计算往往大于实际值；

2) 基于有限元分析对轴承整体分析得应力应变结果并进行寿命仿真，仿真合理性有待探讨；

3) 应力集中部位变形最大，会产生裂纹和磨损；如何预测裂纹拓展和磨损演化以提高轴承寿命值得关注；

4) 轴承寿命分析应多元化，应考虑轴承变形量、游隙、圆度误差等因素对寿命的影响，多模型综合对轴承寿命分析以提高寿命分析精度。

2 轴承寿命理论

2.1 寿命理论发展与运用

20世纪30年代，Weibull寿命分布离散曲线提出[22-23]；40年代，Lundberg和Palmgren两位学者提出载荷容量理论[24]；Stribeck[25]研究疲劳寿命问题，首次对赫兹接触理论进行研究并提出Lundberg-palmgren(L-P)寿命公式；20世纪70年代，FAG公司工程研究中心关于寿命修正问题提出量化寿命理论，结合L-P寿命理论及Miner疲劳损伤累积提出一种修正L-P寿命模型[26]；1984年，Ioannides等[27]提出Ioannides-Harrix(I-H)公式；Tallian[28]基于寿命影响因素于1996年提出Tallian(T)理论；周夕维等[29]基于L-P寿命计算模型对6008型球轴承滚动体尺寸偏差、载荷及游隙等素对寿命影响进行分析计算；Rumbarger[30]在I-H公式的基础上振荡滚动轴承的动态载荷容量、轴承疲劳寿命的计算进行简化；Wu等[31]基于改进的L-P疲劳寿命理论建立疲劳寿命模型来计算分析轴承的疲劳寿命受径向负荷、旋转速度、径向间隙的影响；此外，一些研究人员[32-33]基于其他改进修正的寿命理论对轴承进行多因素寿命分析，其结果优于传统寿命理论。

2.2 寿命理论

1) L-P寿命理论[24,34]

轴承基本额定寿命L10满足：

L10∞(1/P)ε

(1)

式中：ε轴承指数；P为当量动载荷。

P=XFr+YFa

(2)

式中：X、Y为径向、轴向负荷系数；Fr、Fa为径向、轴向负荷。多因素考虑下对额定寿命进行修正，修正额定寿命式如下：

Lna=a1a2a3L10

(3)

式中：a1为可靠度修正系数；a2为承性能修正系数；a3为使用条件系数。

2) I-H 寿命理论[22,27]

I-H寿命理论基于L-P寿命理论提出： L-P简化载荷-寿命关系式为：

Lna=a1a23L10

(4)

式中：a1为可靠度修正系数；a23为I-H修正系数。

3) T寿命理论(数据拟合)[22,28]

根据概率系数来计算轴承寿命：

y=(L/L50)ξln2

(5)

lnln(1/S)=lny

(6)

式中：L为轴承寿命；L50为可靠度50%的寿命；S为使用概率；y为标准化寿命。ξ为威布尔斜率。

以ISO281标准规定的基本额定寿命y10作为基准，则：

y10=(L/L50)ξln(10/9)

(7)

Tallian按照 Lundberg和Palmgren的理论提出最小安全(保证) 寿命Lmin计算公式，即可靠度为100%的使用寿命L0如下：

球轴承(ξ=10/9)：

Lmin=0.009 7L50=0.053L10

(8)

滚子轴承(ξ=9/8)：

Lmin=0.010 2L50=0.055L10

(9)

轴承最小安全寿命约为基本额定寿命的5%。

4) 量化寿命理论[22]

此理论由FAG公司提出：

Lna=a1a23fL10

(10)

式中：a1为可靠度修正系数；a23为修正系数;f为运转条件系数。

5) 寿命理论适应性的优良对比

不同寿命理论下优良适用性比较分析见表1。

表1 寿命理论分析比较

3 基于破坏力学轴承寿命分析模型

3.1 破坏力学研究现状

Lorenz等[35]开发了一个连续损伤力学模型来研究表面粗糙度对不合格接触体滚动接触疲劳寿命的影响；Pandey等[36]开发了基于应变的不同应变比下低周期疲劳的应变连续体损伤模型，以考虑不同应变比对疲劳故障的影响；徐志强等[37]根据断裂力学理论对圆柱形铝合金试件开环绕裂纹的进行扭转试验推算出试件的Ⅲ型裂纹断裂韧度并联合有限元数值计算裂纹尖端附近的应力场；唐娇姣[38]将损伤力学与细观力学模型相结合,建立了材料疲劳寿命预估的损伤力学—有限元解法对缺口件进行疲劳寿命预估以及损伤分析计算；Cano等[39]建立了能够准确地推断出各种合金寿命周期内压力、最小蠕变速率、应变时间连续损伤力学(continuous damage mechanics,CDM)威尔希尔模型；其他研究人员[40-42]陆续将损伤力学联合仿真软件用于各种轴承工件的裂纹预测、损伤预测、寿命预测和疲劳寿命的不确定性评估。

破坏力学的3个发展主要阶段：以强度为指标的古典强度理论、以韧度为指标的断裂力学理论、以渐进衰坏为指标损伤力学理论[43-44]。传统强度理论(图2)认定机械材料强度均匀连续。断裂力学在韧度均匀假设基础上认为缺陷处不连续[44]。

图2 传统强度理论框图

损伤力学认为均匀和连续假设均不成立[43]。破坏力学问题分析如图3所示，损伤力学在工况下分析材料从变形到最后材料破坏、损伤逐渐积累的整个过程；过程中导致不可逆的材料劣化衰坏、部件的材料性能将发生变化、变形会破坏工程材料的力学规律；断裂力学分析裂纹扩展的过程[43-45]。断裂和损伤关系如图4所示。

图3 破坏力学分析问题框图

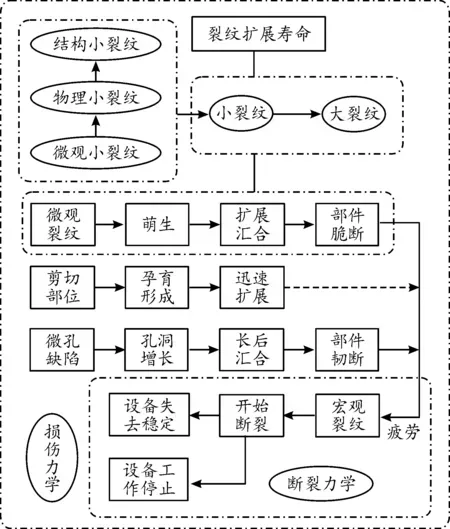
图4 断裂力学与损伤力学关系框图

3.2 断裂力学轴承接触疲劳寿命模型

何芝仙等[46]提出采用“等效直径法”建立具有弹性曲轴裂纹有限元模型来研究具曲轴-轴承系统动力学、摩擦学、断裂力学耦合问题，并运用插值法对耦合问题进行解耦；潘琦[47]在滚动体接触面通过轴承模型建立裂纹来计算分析轴承的应力和应力强度因子等参数，探讨表面裂纹对轴承整体性能的影响；一些研究人员[48-49]将断裂力学引入轴承分析只停留在应力强度因子、应变分析之上，并未将裂纹拓展与疲劳寿命相结合，因而不能有效精准地预测轴承寿命。

采用线弹性断裂力学理论对轴承进行疲劳裂纹扩展研究，断裂力学认为裂纹源于轴承疲劳缺口根部位置[44-45]。从短裂纹出发考虑初始裂纹长度：

x0=(ΔKth/FCEΔεe)2/π

(11)

式中：ΔKth裂纹门槛应力强度因子，F为几何因子，C为形状修正因子，Δεe为疲劳应变幅。

对于缺口根部先产生裂纹所形成的非扩展裂纹的锐缺口的疲劳应力集中系数Kf[43-45]为：

(12)

断裂力学模型下的Kf考虑了缺口的尺寸效应。对于缺口根部先不产生非扩展裂纹的钝缺口的疲劳应力集中系数Kf为[43]：

(13)

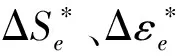
等效应力强度因子K可以表示裂纹端部的应力强度：

(14)

在等效应力强度因子的基础上，根据修正Paris的Forman公式计算出疲劳寿命[43-45]：

da/dN=[C(K)n]/[(1-R)KC-K]

(15)

式中：a为裂纹尺寸；N为疲劳循环次数；C、n为试验测定材料系数，n=2～4。

若轴承承受恒定载荷：

(16)

Nf=N-N0

(17)

式中：x0为初始裂纹尺寸;af为临界裂纹尺寸；当x0为初始裂纹尺寸时N0=0；N为裂纹扩展至临界尺寸的循环次数；Nf为疲劳寿命。

据介绍，该国学博览馆是国内首家纯公益性国学博览式文化传播机构。宏光集团公司董事局主席张辉在开幕致辞中说，国学博览馆的使命就是为了传承和弘扬中华传统文化，为中华民族的复兴贡献力量。张辉说：“现在我们的物质生活已脱离贫困，而精神世界还需不断丰富。让我们在历代先哲的圣德名言中知行合一。在传承民族文化的道路上，国学博览馆愿与君共勉！”

3.3 损伤力学轴承接触疲劳寿命模型

谢阶栋[50]基于轴承接触疲劳耦合损伤模型计算了不同工况下球轴承径向载荷、润滑、缺陷、滚动体数量、转速对滚动轴承寿命影响；陈跃良等[51]建立了轴承钢材料试验模型来计算腐蚀坑位置、尺寸、腐蚀分布等参数，分析冲击载荷下点蚀损伤对30CrMnSiNi2A钢应力集中的影响；杨梦科等[52]运用多体动力学建立可预测轴承局部缺陷尺寸等参数的动力学模型并研究缺陷参数对轴承振动。寿命为轴承重要指标，各类影响因素都可反馈至寿命[53]。一些研究人员[54-55]从各方角度切入，探讨轴承损伤机理，忽略损伤演化过程，且不能将损伤演化与寿命联系。从损伤演化机理入手，探讨损伤演化过程演化与寿命的联系，可以更好地分析预测轴承寿命。

轴承材料的损伤本构关系与其在正常无损状态下的本构关系形式一致，其真实应力由有效应力代替[44-45]。则三维拉应力下基于各项同性状态假设的本构方程[43]为：

σij=2μ(1-Dμ)εij+λ(1-Dλ)εkkδij

(18)

式中：σij为应力张量；λ为材料的梅拉常数，μ：λ=Ev/(1+v)(1-2v)、μ=E/2(1+v)，其中v为泊松比、E为弹性模量；Dμ、Dλ为损伤变量(D∈(0，1))；εij、εkk为弹性应变(ε)；δij为K-d函数。

滚动轴承接触疲劳是高周疲劳。Chaboche对高周疲劳状态下提出损伤演化方程[44-45]：

dD/dN=[σ/B(1-D)]βf(D)

(19)

f(D)=[1-(1-D)1+β]α

(20)

(21)

式中：B、α、β可通过材料疲劳试验来测定；材料初始损伤为0，即D=0时，N=0；当轴承材料疲劳损伤破坏,理论视作D=1；Nf为疲劳寿命。

3.4 损伤力学和断裂力学联合有限元对轴承疲劳寿命分析的新思考

3.4.1损伤力学和断裂力学寿命评估分析探讨

滚动轴承运转过程中出现的疲劳剥落、裂纹萌生、扩展是可预测和可定量分析的[45,56]。目前，所采用的疲劳寿命工程计算预估方法无法细致探究零件的疲劳损伤累积的过程，普通工程疲劳计算预测可靠性较低，且与实际偏差太大[3]。一些工程研究人员关于影响因素的研究单一片面，不能很好地将寿命影响因素的计算结果反馈至寿命并与寿命建立联系。

从断裂力学评估方法角度出发，可以有效提高轴承疲劳抗力特性[43-44]；从损伤力学角度出发，考虑疲劳剥落由萌生、扩展至最后失效的全寿命周期，损伤力学的引入可研究微裂纹的演变，由宏观裂纹形成至轴承完全破坏的裂纹整个过程，可以弥补微观研究和断裂力学研究的不足[44,45,52]。有限元分析能灵活处理和求解实际工程问题，但与实际偏差较大[17,22,40]。

基于损伤力学和断裂力学双角度联合有限元分析结果的方法能够将轴承结构应力危险部位计算的可靠度提高，三者之间优缺点互补，说服力更高，轴承零件的疲劳损伤累积数值计算将更趋于真实；寿命评估结果精度也越高。滚动轴承断裂力学与损伤力学分析展望如图5所示。

3.4.2一种寿命评估新思路的提出

基于滚动轴承断裂力学与损伤力学分析(图5)，从断裂力学和损伤力学双视角出发，利用2种力学模型优缺互补提出寿命评估的新思路，双模型优缺互补，双角度评估寿命，并考虑不同轴承游隙、不同内圈圆度误差对疲劳寿命的影响、轴承变形与疲劳寿命的关系，说服力更强。轴承裂纹以及磨损性能的分析可以有效分析轴承疲劳性能，实现应力-应变场与裂纹拓展的联系、轴承疲劳损伤与应力-应变场的计算耦合、多因素综合评估轴承疲劳寿命，并联合有限元计算、理论计算、结合试验佐证用以综合评估轴承疲劳寿命。该思路的提出可较大地提高疲劳寿命预测精度，也可极大地反映轴承材料断裂、损伤导致的轴承部件不可逆衰坏的过程。寿命评估新思路如图6所示。

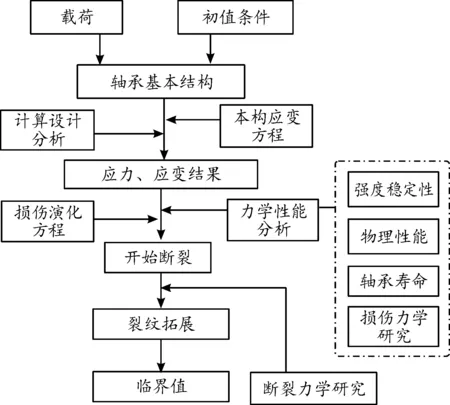
图5 滚动轴承断裂力学与损伤力学联合分析展望框图

图6 基于滚动轴承断裂力学与损伤力学疲劳寿命分析新思路框图

4 结论与展望

从寿命与破坏力学角度出发，就轴承疲劳寿命计算预估过程以及基于断裂力学和损伤力学计算模型在轴承寿命中的运用进行概述和分析：

1) 综述了轴承疲劳寿命研究现状与疲劳寿命理论、寿命计算公式；并对寿命理论的优劣作比较分析，L-P理论是普遍适用，I-H寿命理论考虑因素众多，与实际更为接近。

2) 对目前轴承寿命问题研究不足及发展趋势作了探讨：在传统接触探讨理论计算接触载荷、应力、弹性趋势等问题基础上，可运用基于有限元分析对轴承整体分析得应力应变结果并进行寿命仿真，且结合应力集中部位进行裂纹扩展和损伤演化分析相关的寿命预测。

3) 综述了断裂力学和损伤力学寿命计算模型，探讨工程应用中断裂力学与损伤力学关系；对基于损伤力学和断裂力学模型联合有限元对轴承疲劳寿命进行分析展望。

4) 基于破坏力学在滚动轴承中的应用探讨和分析展望，从断裂力学和损伤力学双角度联合有限元出发，探讨游隙、内圈圆度误差、变形量与对疲劳寿命间的关系，基于最大应力部位，提出一种断裂力学和损伤力学联合有限元轴承疲劳寿命评估的新思路，用断裂裂纹扩展和损伤演化以评估预测轴承的疲劳寿命，并以理论计算与试验相结合佐证分析，为轴承寿命分析提供思路借鉴，对提高疲劳寿命精度分析具有一定的指导意义。

回望滚动轴承寿命理论与寿命分析流程的进展，随着计算机技术的进步、分析方法的改进、仿真与试验模型的越来越合理有效、试验设备的完善、数据结果分析的优化，所得结果越来越贴近真实数值。轴承疲劳寿命评估的不断改进对后续轴承寿命分析、确保设备安全运行、轴承行业的发展具有重要意义。基于上述研究，针对如何实现寿命分析精准和疲劳寿命分析模型合理化，未来研究将从以下4个方向努力：

1) 目前在寿命研究中，对轴承游隙、润滑、力作用下内外圈的椭圆度变形等寿命影响因素并未考虑，其所得结果远远大于实际寿命值。寿命外界因素的考虑可以通过模型三维合理建立，也可以导入有限元模型引入添加，亦可以通过其他模型辅助，用以建立趋近真实承载的轴承外界环境来提高疲劳寿命分析精准。

2) 在应力集中部位，轴承失效体现在疲劳磨损与裂纹萌生至断裂，精准预测裂纹的拓展和轴承损伤的演化势在必行。设计更精准的仿真模型、提高应力强度因子计算精确度、构建合理的损伤演化方程，是未来应该努力的方向。

3) 利用现有软件进行联合仿真，并研发专用软件，为轴承裂纹分析、损伤分析和疲劳寿命分析提供专业保障。

4) 对轴承裂纹、损伤、疲劳寿命分析试验方法进行研究和优化，并对专用试验设备进行开发研究，为理论和仿真结果提供合理的试验佐证。

综上，未来轴承研究应致力于疲劳寿命的精准分析和分析模型合理化，使轴承以更好的稳定性、更高的转速、更长的寿命广泛应用于设备。