过渡金属Fe、Co掺杂二维CuI的第一性原理计算*

王 一，姚登浪,3，宋 娟，王继红，罗子江，丁 召，郭 祥,3

(1. 贵州大学 大数据与信息工程学院,贵阳 550025; 2. 教育部半导体功率器件可靠性工程中心,贵阳 550025;3. 贵州省微纳电子与软件技术重点实验室,贵阳 550025; 4. 贵州财经大学 信息学院,贵阳 550025)

0 引 言

从2004年石墨烯问世以来，单个或者数个原子厚度的二维材料在学术界引起了关注，越来越多的人投入到了二维材料的研究当中[1]。随着制作工艺的成熟，越来越多的二维材料被合成出来，比如金属硫族化合物[2]、过渡金属碳/氮化合物[3]、硅烯[4]等。由于具有平滑的表面结构、可调的带隙范围、较大的比表面积等优异特点使得二维材料的研究涉及众多领域，包括离子电池[5-6]、催化剂[7]、超级电容[7]、光电器件[7]等等。碘化亚铜(CuI)作为一种Ⅰ～Ⅷ的碘化物材料，是带隙为3.1 eV的直接带隙半导体材料[8]。CuI拥有较高的激子束缚能和较小的空穴有效质量，具有优异的p型导电特性[9]，因此在半导体光电器件领域表现出潜在的应用前景，比如作为空穴传输材料广泛应用在光伏电池领域[10-11]，作为有机半导体场效应晶体管的栅电极等[12]。

二维(Two-dimensional, 2D)CuI结构于2018年由Kangkang Yao等人通过物理气相沉淀法在SiO2/Si衬底上成功合成，研究表明2D CuI具备低电阻率的特征[12]。此外，研究团队进一步发现2D CuI可以在2D WSe2、2D WS2上生长形成范德瓦尔斯异质结构，并且其形成的异质结构具备明显的电流整流的特性。众所周知，过渡金属掺杂是一种很有前途的、有效的调控二维材料的光电性质以及自旋特性的方法[13-17]，如对于石墨烯上过渡金属原子的掺杂，Sevinçli等人发现Fe或Ti的吸附使得石墨烯在费米能级上具有100%自旋极化的半金属化[18]；Zhou等报道了BN单分子膜(BN-ML)对Fe的吸附为半金属，对Co的吸附为窄禁带半导体[19]；李佳斌利用密度泛函理论计算了过渡金属掺杂类石墨烯2D GaN结构的光电性质，其计算结果表明过渡金属原子的掺杂使2D GaN能带的斜率发生变化，并且2D GaN与掺杂原子之间存在一定的电荷转移[20]。虽然2D CuI在实验上已经成功制备，但是针对有关于2D CuI掺杂后物性的变化尚未清晰，因此依据第一性原理展开对2D CuI结构的理论计算探究其基本物理特性以及掺杂对其基本物理特性的影响显得尤为重要。不仅如此，为了能调整2D CuI结构的电子结构和光学性质，对于进一步拓展其应用领域具有实际意义。

本文基于第一性原理计算了本征2D CuI以及过渡金属(Fe、Co)掺杂后的2D CuI的电子结构，光学性质以及磁学性质，以期为后续的理论研究，实验制备以及实际应用提供指导。

1 计算模型与方法

CuI拥有α、β、γ 3种晶相，其在常温下存在的形式为立方性结构γ-CuI 形式[21-23]。本文计算所用的(4×4×1)2D CuI结构是将优化后的γ-CuI的(111)面截面后沿得到的二维结构的a以及b基矢方向分别扩胞4倍所得，然后在垂直于2D CuI表面的c方向加1.5 nm的真空层，得到的本征2D CuI结构如图1(a)所示，其中Cu和I原子分别有16个。分别用一个Co和Fe原子替换2D CuI结构中的任意一个Cu原子，替换后的结构图如图1所示。

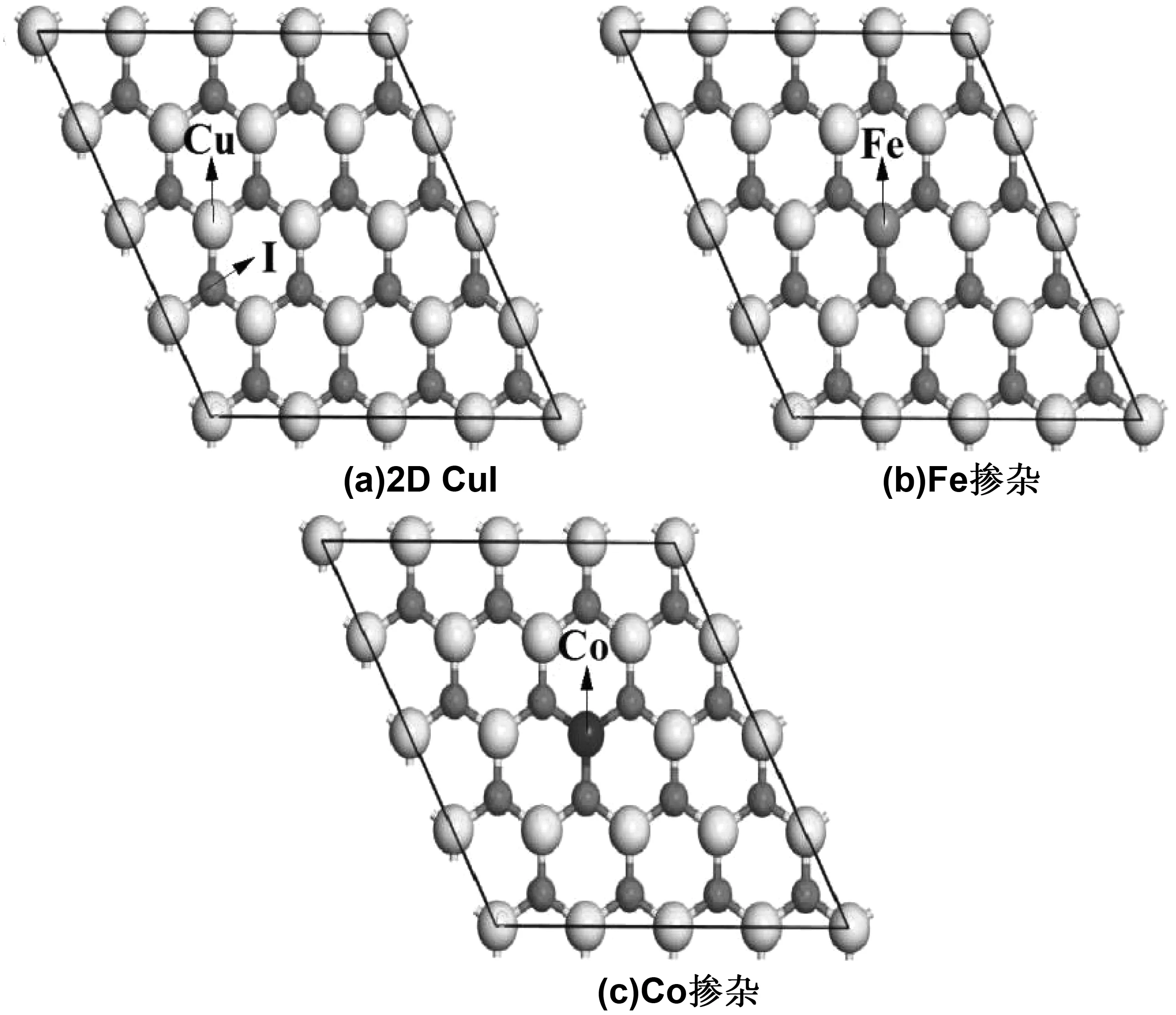
图1 结构示意图

本文的所有计算均是基于密度泛函理论的Cambridge Sequential Total Energy Package (CASTEP)软件包完成，2D CuI和Fe、Co掺杂后的2D CuI的k采样密度以及截断能分别设置为400 eV以及4 ×4×1，结构优化均利用Broyden-Fletcher-Goldfarb-Shanno(BFGS)算法以及GGA-PBE泛函，并且将优化的4个参数如原子间最大相互作用力、原子最大位移收敛标准、作用在每个原子上的最小力以及自洽精度的设置分别为：0.3 eV/nm、0.0001 nm、0.05 GPa、1.0×10-5eV/atom。

2 结果与分析

2.1 几何优化结果分析

表1为2D CuI以及Co以及Fe掺杂后2D CuI的键长，布居值以及磁矩表。由表1键长数据可知，Co以及Fe的掺杂使2D CuI的Cu-I键变长，且Fe掺杂后使Cu-I键长大于Co掺杂后Cu-I键长；Fe-I键长大于本征2D CuI中Cu-I键长，这可能是由于Fe的原子半径明显大于Cu的原子半径产生的影响。从表中布居值数据可知，与本征2D CuI相比，Fe、Co掺杂2D CuI后Cu-I键之间的布居值变小，由布居值的定义：布居值越大，共价键越强、离子键越弱；反之则共价键越弱、离子键越强，可以看出在Fe、Co掺杂后Cu-I共价键变弱。在Fe、Co替位掺杂后，Fe-I、Co-I键之间的布居值均大于本征2D CuI中Cu-I键的布居值，这表明Fe-I、Co-I共价键更强。此外 Fe、Co的掺杂使2D CuI体系分别引入了2.99 μB、1.96 μB的磁矩，这主要是由于Fe和Co的3d轨道未被电子填满所引起。

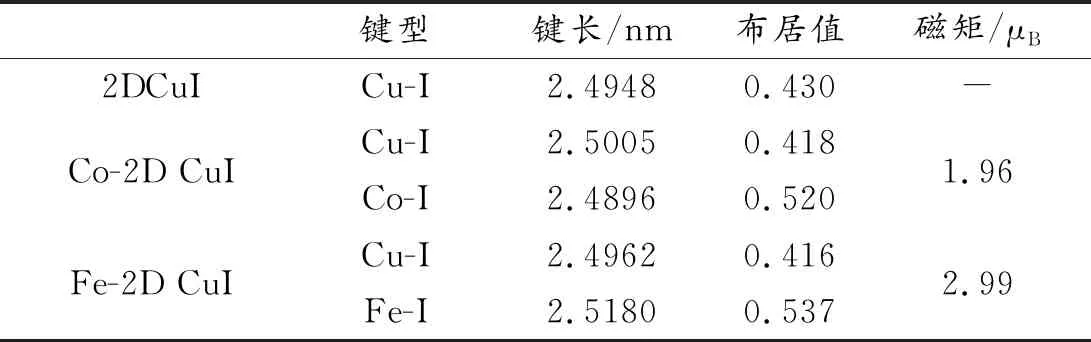
表1 2D CuI以及Co、Fe分别掺杂2D CuI的键长，布局值以及磁矩

2.2 电子结构及光学性质

2.2.1 能带结构

图2和图3展示了2D CuI以及Co和Fe掺杂后2D CuI的能带结构图。 图2(a)为2D CuI的能带结构图，从图中可以看出能隙值Eg=1.61 eV，其价带顶和导带底均位于布区中心点G处，表明2D CuI为直接带隙材料，从态密度图中可以看出对于价带底而言，主要是来自于Cu-d轨道以及少量的I-p轨道的贡献，对于导带而言则是由Cu-p轨道以及I-s轨道sp2杂化贡献。

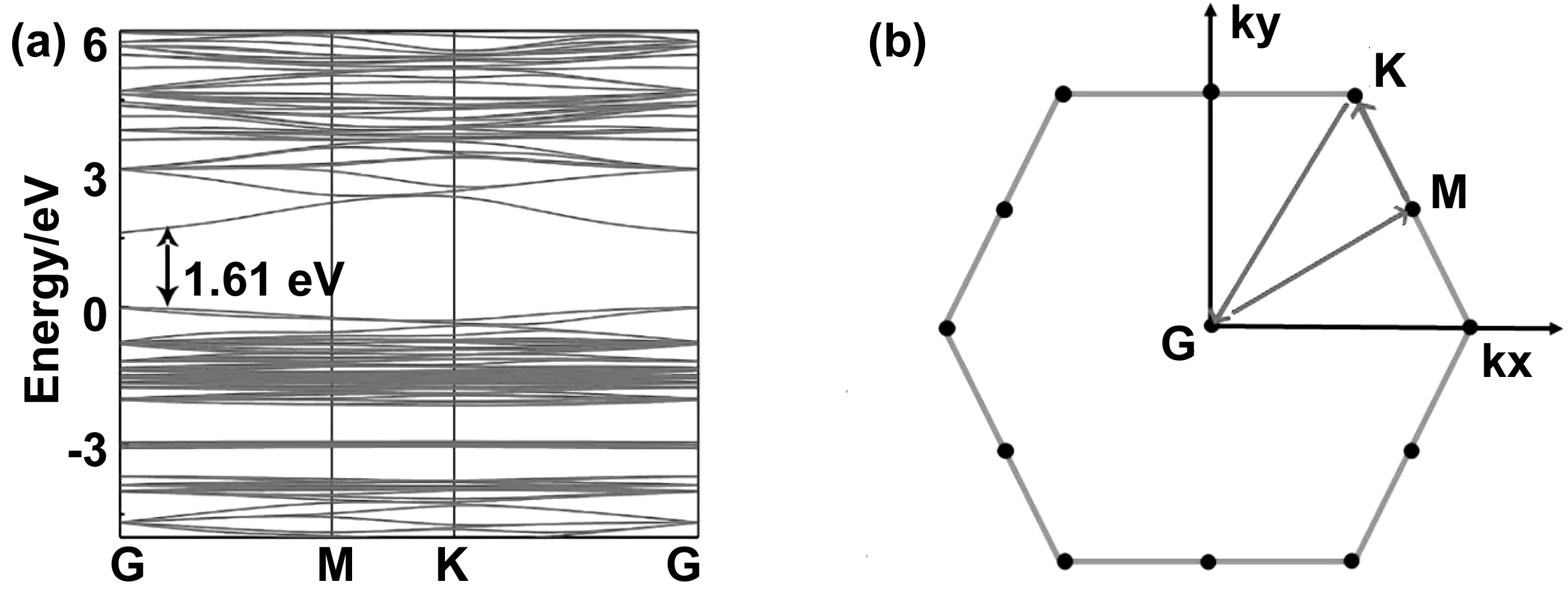
图2 2D CuI的能带结构图以及能带计算时k空间的路径

图3(a)、(b)分别为Co、Fe掺杂2D CuI的能带结构图，图中红色和蓝色曲线表示自旋向上和向下的能带。从图3(a)可以看出，Co的掺杂在自旋向下的能带中引入了4条施主杂质能级，分别为EA1、EA2、EA3、EA4，其中EA1和EA2为靠近导带底，为浅施主能级，二者的电离能分别为0.061及0.146 eV，这意味着位于EA1以及EA2能级上的电子只需吸收0.061及0.146 eV的能量便能跃迁至导带成为载流子。EA3和EA4靠近价带顶，为深施主能级，二者的电离能为1.188和1.976 eV，对2D CuI导电性影响较小，但是引入的深施主能级是有效的复合中心，有利于电子与空穴的湮灭。此外，从Co掺杂2D CuI的能带图中可以得知Co掺杂后引入的施主能级均位于自旋向下的能带图中，且它们均是来自于Fe-d轨道的影响。

图3(b)可以看出Fe的掺杂在2D CuI结构中引入了两条施主杂质能级，分别为EB1和EB2，二者的电离能分别为0.77及0.935 eV，这意味着这两条杂质能级属于深施主能级，这对2D CuI结构的导电性几乎不产生影响，且Fe掺杂引入的施主能级均位于自旋向下的能级中，主要来自于Fe-d轨道的影响。无论是从Fe掺杂而言还是Co原子掺杂而言，二者引入的施主能级均位于不同的能量位置，这意味着杂质能级上的电子挣脱原子和的束缚所需要的能量有所区别，通过分析，可以得出这主要是来自于以下几个原因的影响：(1) 由于核外电子所处的原子轨道不同所导致(最外层带着挣脱束缚所需的能量小于内层电子)；(2)由于核外电子之间的库伦排斥力的作用导致第一个核外电子挣脱原子束缚时所需的能量小于剩余电子挣脱原子束缚所需的能量；(3)当电子挣脱原子束缚后，导致中性态的原子成为正电中心(离化态)，从而因库伦引力的作用增强了对核外电子的束缚；进而导致电子的电离能增大。

图3 能带结构图(a)Co掺杂2D CuI；(b)Fe掺杂2D CuI

2.2.2 态密度

图4是2D CuI和Co以及Fe掺杂2D CuI在能量范围为-15～20 eV的总态密度与分波态密度。对于2D CuI而言，可将总态密度图分为3个能量区间进行讨论，分别为-14.18～-12.36 eV、-5.86～0.97 eV和0.97～-20 eV。对于-14.18～-12.36 eV的能量区间而言，对2D CuI的总态密度贡献主要来源于I-s态；对于-5.86～0.97 eV的能量区间而言，对总态密度的主要贡献是Cu-d态和I-p态；对于0.97～20 eV的能量区间而言，对2D CuI的总态密度的主要贡献主要来自于Cu-s/p态和I-s/p态电子。在掺杂后，-14.5～-10.5 eV区间，对态密度的贡献主要来自于I-s态，对2～15 eV态密度的贡献主要来自于Cu-p态，I-s态，还有杂质的p态。相较于本征2D CuI而言，Co和Fe原子掺杂后在-7～2 eV对总态密度的贡献主要来自于Fe-d轨道，Co-d轨道，Cu-d轨道以及少量的I-p轨道。

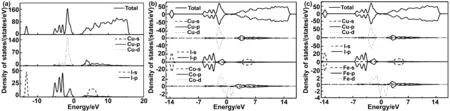
图4 总态密度与分波态密度(a) 本征 2D CuI; (b)Co 掺杂 2D CuI ；(c)Fe 掺杂 2D CuI

2.2.3 光学性质

图5展示了2D CuI以及Co、Fe掺杂2D CuI后的复介电函数。介电函数ε=ε1(ω)+ε2(ω)可以用来描述材料的光学性质，其中实部ε1(ω)反应材料的介电特性，虚部ε2(ω)反应材料的光吸收特性。图5(a)为介电函数的实部ε1(ω)在光子能量范围为0～5 eV的变化曲线。经计算得出2D CuI以及Fe、Co掺杂后的静态介电常数ε1(0)分别为：2.57、2.47、2.42，可以看出Fe、Co的掺杂使得2D CuI体系的实部介电函数ε1(ω)的静态值高于本征2D CuI，且Fe掺杂后使2D CuI体系的静态值变得更大，达到了2.57，根据电容和静介电函数的关系C∝Aε1(0)(A为比例系数)，可以得出Co和Fe的掺杂增加了2D CuI的电荷储存能力，但是同时也增加了寄生电容，这对基于2D CuI半导体材料的高频器件的性能有一定的影响。随着光子能量的增加，实部ε1(ω)增加后减小，其峰值为：2.68、2.68、2.60，对应的能量均为1.44 eV；当光子能量在2.5 eV附近时，实部ε1(ω)的值继续增加，达到峰值后持续减小，其峰值为：2.77、2.68、2.68，对应的光子能量均为3.75 eV。

图5(b)为介电函数的虚部ε(ω)在光子能量范围为0～4.5 eV的变化曲线。可以看出在掺杂前后曲线的变化趋势基本一致，均随着光子能量的增加而增加。在可见光范围内，Fe的掺杂使2D CuI体系的光吸收特性变得更好，其次是Co的掺杂，最后是纯净的2D CuI。

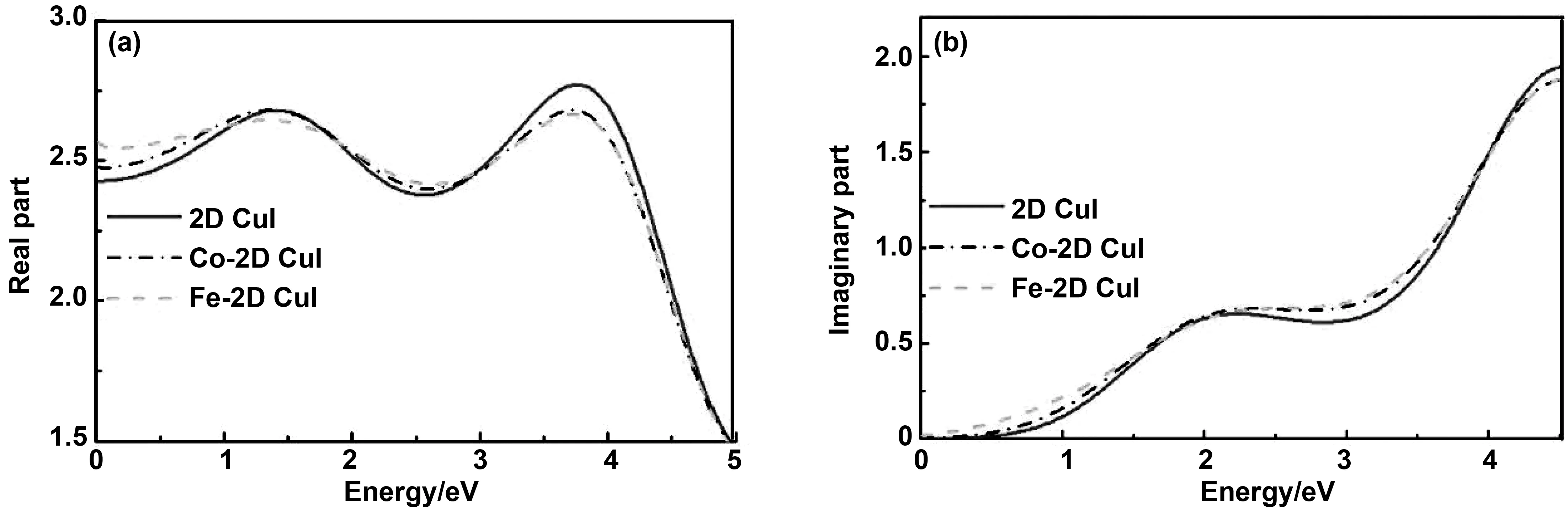
图5 2D CuI和Co、Fe掺杂后2D CuI的介电函数的(a)实部曲线(b)虚部曲线

图6为2D CuI以及Co、Fe掺杂后的2D CuI在光子能量范围为0～3.75eV的反射系数曲线图。2D CuI以及Co、Fe掺杂后的2D CuI的静态反射系数为0.048、0.050、0.054，这表明Co、Fe的掺杂使2D CuI的透射率减弱。在0～0.75 eV范围内，2D CuI的反射系数从0.048开始持续增加；Fe的反射系数从0.054降低到0.0525后再上升，此时对应的光子能量为0.167 eV；Co的反射系数从0.050降低到0.0496后再上升，此时对应的光子能量为0.0415 eV。在光子能量范围为1.6～3.1 eV中，Fe的掺杂使2D CuI的反射系数变得最大，其次是Co，最后是纯净2D CuI，这表明在可见光范围内，Fe、Co的掺杂会降低2D CuI的透射系数。

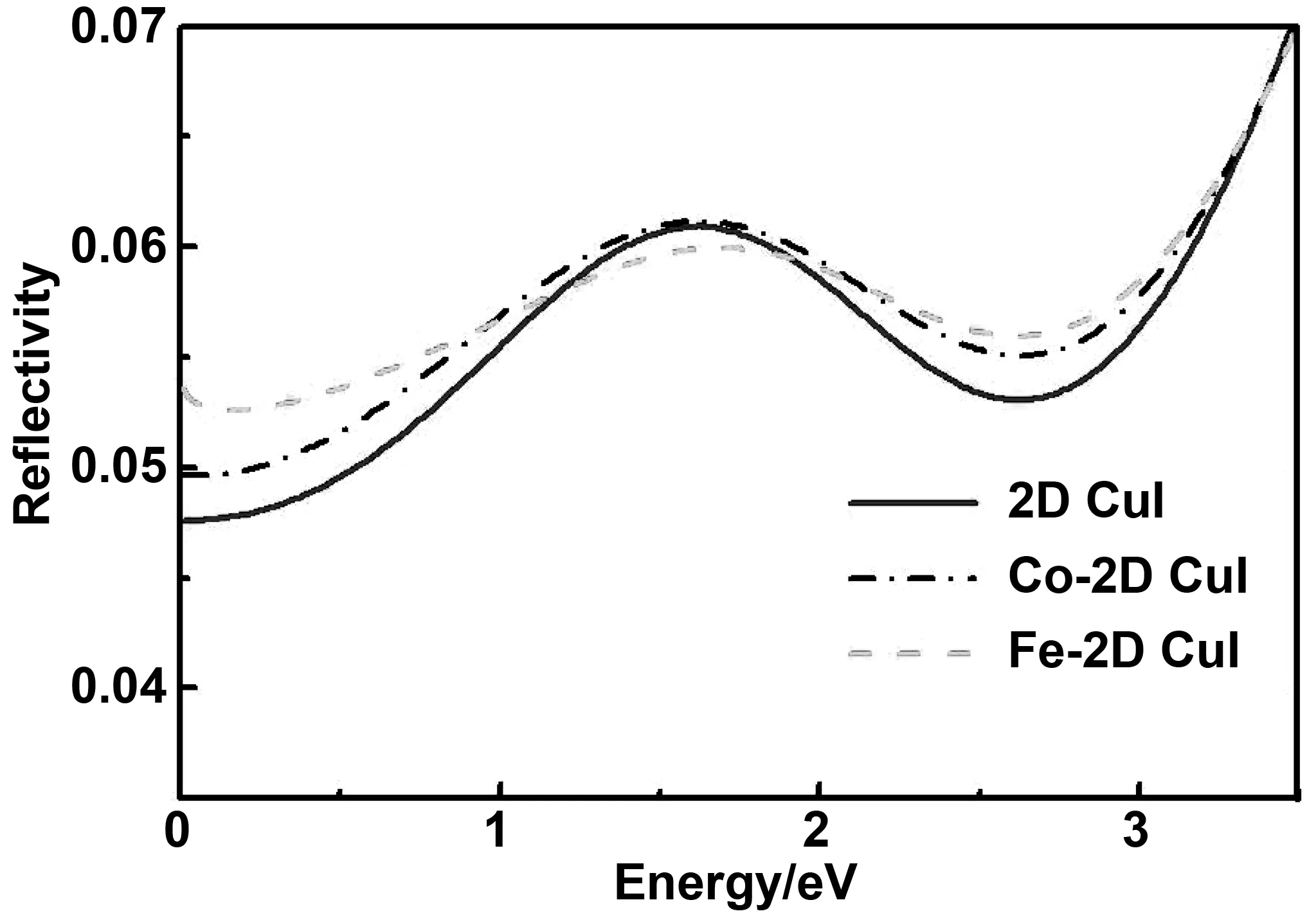
图6 2D CuI以及Co、Fe掺杂2D CuI后的反射系数变化图

3 结 论

通过密度泛函理论计算了2D CuI以及Fe、Co掺杂2D CuI后的磁矩、能带结构、态密度、介电函数、反射率等基本物理特性。计算结果表明2D CuI的带隙为1.61 eV，为直接带隙半导体材料，Co掺杂在2D CuI中引入了两条浅施主能级以及两条深施主能级，从而增加了载流子的浓度；Fe掺杂后引入了2条施主能级，这意味着Fe掺杂不影响2D CuI的导电性； Fe、Co的掺杂使2D CuI体系引入了2.99 μB、1.96 μB的磁矩，这主要来自于Co和Fe原子3d轨道的影响；光学性质的计算结果表明Fe以及Co掺杂使2D CuI体系在可见光范围内光吸收特性变得更好，透射系数变低。