电熔镁砂熔炼过程电极电流饱和约束一步最优控制

富 月 李 宝

电熔镁砂熔炼过程如图1 所示,首先,将菱镁矿石运送至原矿仓,然后,经电振给料机将菱镁矿石加入电熔镁炉中,通过供电系统供电,使A、B 和C 三相电极末端产生电弧,菱镁矿石吸收电弧放出的热量融化,形成熔池.电流控制系统通过产生电流以控制电机,使三相电极上下移动,进而使三相电极电流跟踪其设定值,随着菱镁矿石的不断加入以及不断融化,熔池液面的高度不断上升,当熔池的上表面达到炉口时,熔炼过程结束.最后,使用工具车将电熔镁炉的炉体脱离熔炼工位,进行冷却和处理,从而获得电熔镁砂产品[1].

图1 电熔镁砂熔炼过程Fig.1 Fused magnesia smelting process

电熔镁砂熔炼过程以三相电机转动方向与频率为输入,以三相电极电流为输出,采用埋弧方式,即将三相电极埋入原矿中,边熔化边加料,具有工艺机理复杂、关键参数不能测量、受原料成分和生产条件等不确定因素干扰、熔炼过程动态变化等综合复杂性.针对电熔镁砂熔炼过程,文献[1]根据能量守恒定律,建立了电极电流动态模型.

该模型是一类具有未知参数的仿射型离散时间非线性模型,针对该类模型,从上个世纪90 年代开始,随着神经网络和模糊逻辑等智能工具的引入,很多学者开展了相关控制方法的研究.文献[2−3]为最早将多层神经网络和模糊逻辑引入到离散时间非线性仿射系统控制问题的文献.在此基础上,文献[4] 基于一定的假设条件,提出了新的多层神经网络自适应控制方法,并给出了收敛性结果;文献[5−6]提出了基于神经网络与自适应动态规划的近似最优控制方法;文献[7]提出了基于单层神经网络的有限水平单网络自适应控制方法;文献[8]提出了基于神经网络的有限时间最优控制方法;文献[9] 提出了一种新颖的非策略交错式Q 学习算法,并证明了收敛性;文献[10−11]提出了基于神经网络的容错控制方法;文献[12−13]提出了自适应模糊控制方法;文献[14]利用两种模糊规则仿真网络建立系统动态模型,提出了一种自适应控制方法;文献[15]利用直接补偿法,提出了一种多开关自适应线性化模糊控制算法,用于延迟非严格反馈系统,等等.上述基于神经网络和模糊逻辑的非线性控制方法,算法复杂,很难在电熔镁炉等复杂的工业过程中进行实际应用.为了实现电熔镁炉的自动控制,文献[1]设计了带输出补偿的PID 控制方法.该方法根据电熔镁砂熔炼过程电极电流对象模型,首先将其在平衡点附近线性化,得到由线性模型和未知高阶非线性项组成的控制器设计模型,然后根据该控制器设计模型设计带输出补偿的PID 控制器,最后用一步最优前馈控制律和一步最优调节律设计控制器参数.由于没有考虑实际电机转动频率的约束,并且控制器设计模型和对象模型之间具有较大的误差,使得电流跟踪其设定值的误差较大.

本文通过引入中间变量并转化控制目标,将电熔镁砂熔炼过程三相电极电流的复杂非线性控制问题简化为线性控制问题,提出了一种简化的电极电流饱和约束一步最优控制方法.“一步最优控制”与“一步预报”相对应,基于“一步预报”的控制即为“一步最优控制”[16].经典的一步最优控制算法不能应用于具有饱和约束并且存在外部干扰的实际非线性过程.本文通过引入拉格朗日乘子向量和松弛向量验证了该方法的最优性.此外,当考虑电熔镁砂熔炼过程中存在的不可测外部干扰时,在上述简化的电极电流饱和约束算法的基础上设计了高阶干扰观测器,提出了具有高阶干扰观测器的简化算法.

本文的主要创新点如下:

1) 针对电熔镁砂熔炼过程三相电极电流的复杂非线性控制问题,通过引入中间变量并转化控制目标,将其转化为线性控制问题;

2) 通过引入拉格朗日乘子向量和松弛向量,提出了一种简化的电极电流饱和约束一步最优控制方法,解决了电熔镁砂熔炼过程中电极电流的饱和约束控制问题;

3) 设计高阶干扰观测器,提出了基于高阶干扰观测器的饱和约束一步最优控制方法,解决了电熔镁砂熔炼过程中存在不可测干扰的电极电流饱和约束控制问题.

1 控制问题描述及控制目标转化

针对电熔镁砂熔炼过程,文献[1]根据能量守恒定律,建立了如下电极电流动态模型:

采用欧拉法对模型(1) 进行离散化[17],由于Fi(·)和Qi(·) 随时间变化缓慢,因此可假设其为常数,由此产生的建模误差由电流的变化率 ∆yi(k) 来补偿,故式(1)的离散化模型可表示为式(2)[1]:

其中,σt=1 s为采样时间,∆=1−z−1,z−1为单位后移算子.

电熔镁砂熔炼过程中电极电流动态模型的输入变量ui(k),即三相电机转动方向和频率在实际运行过程中会受到执行器的饱和约束.本文的目标为针对电熔镁砂熔炼过程电极电流动态模型(2),设计饱和约束一步最优控制器,使得电极电流跟踪其设定值,并且控制器输出满足饱和约束,即|ui(k)|≤m,其中m>0 为电机转动方向与频率的上界,并且已知.不失一般性,首先针对式(2),做如下假设:

表1 电极电流动态模型中参数的符号及物理意义Table 1 Symbols and meanings of parameters in dynamic model of electrode current

假设 1.系统输出电极电流yi(k)0.

式(2)为仿射型非线性模型,通过观察,我们发现将式(2)等号左右两边同时除以,经过整理可以得到:

2 饱和约束一步最优控制

针对式(4),为了实现系统输出渐近跟踪其设定值,尽可能降低控制输入幅值,使其满足饱和约束,同时消除ai对系统输出的影响,现引入一步超前最优性能指标:

其中,P(z−1)、R(z−1)、Q(z−1)和S(z−1) 为加权多项式.P(z−1)和Q(z−1) 的选择保证了闭环系统在输入饱和约束下的稳定性,通过选择R(z−1) 来消除跟踪误差,通过选择S(z−1) 实现对ai的静态补偿.为了表述方便,我们令其中求解饱和约束一步最优控制律,就是求解如下带不等式约束的条件极值问题:

采用拉格朗日松弛法,通过引入拉格朗日乘子参数α ≥0和β ≥0 以及松弛参数µ和v,将条件极值问题转化为如下不带约束的极值问题:

其中,J′=J+α[ui(k)−m+µ2]+β[−ui(k)−m+v2] .

定理 1.饱和约束一步最优控制律为:

其中,D=Fbi+Q0,通过下式计算:

证明.引入Diophantine 方程:

其中,F为常数,G(z−1) 为1 阶多项式.用F乘以式(4)等号左右两边,并利用式(10),可以得到:

于是由式(7)和式(11)得J′对ui(k) 的偏导为:

令D=Fbi+Q0,并将式(11)代入式(12),则

J′对α、β、µ和v的偏导分别为:

令式(13a)～ (13e)为零,则可以得到:

证明.考虑如下两种情况:

为了实现稳态跟踪,由式(15a)可知,需要选择S(z−1),使Q(z−1)−S(z−1)bi=0,并选择R(z−1)使闭环系统的稳态增益为1.

由式(15a)可知,为了使输出xi(k) 能够稳定跟踪设定值,多项式S(z−1) 和R(z−1) 必须满足:

当系统达到稳态时,式(15a)可以写为:

注 1.不难看出,控制器(8)实际上是饱和约束控制的解析形式.控制系统结构如图2 所示.可以看出,该控制系统由常规控制器、饱和约束控制器及被控对象三部分构成,其中常规控制器由前馈控制和反馈控制两部分组成,饱和约束控制器由拉格朗日乘子向量和饱和约束组成,反馈信号为虚拟变量 .xi(k)

图2 饱和约束一步最优控制结构图Fig.2 Structure diagram of one-step optimal control with saturation constraint

3 基于高阶干扰观测器的饱和约束一步最优控制

在电熔镁砂熔炼过程中,通常会受到原料成分和生产条件等不确定性的外部干扰影响,导致系统性能变差.当考虑不可测外部干扰di(k) 时,经过整理可以得到与式(4)相对应的电熔镁砂熔炼过程对象模型如下:

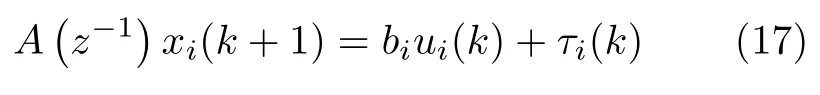
其中,N为正整数,是高阶干扰观测器的阶次,为k时刻系统的干扰估计,为k时刻系统的输出估计,Lj ∈R 是常数,其中j=0,1,2,···,N,

假设2.未知干扰di(k) 有界,并且其变化率满足∆di(k)<1.

定理 3.若假设2 成立,并且存在常数Lj,j=0,1,2,···,N,使得对于任意的|z|>1,不等式则对于任意小的正数ε>0,存在正整数N0,当N>N0时,干扰估计误差其中,E

证明.对于任意k时刻的干扰di(k),可以将其扩展为:

将式(19)和式(18a)相减,整理,可以得到:

由式(17)和式(18b)可以得到:

将式(21)代入式(20),可以得到:

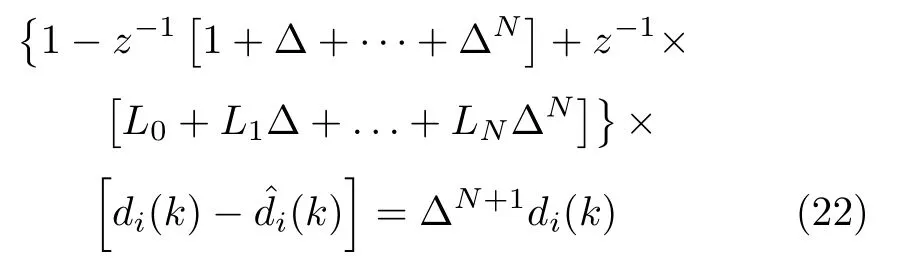
令E(z−1)=1+∆+···+∆N,T(z−1)=L0+L1∆+···+LN∆N,则式(22)可写为:

根据第2 节饱和约束一步最优控制设计过程可以得到基于高阶干扰观测器的饱和约束一步最优控制方程为:

4 仿真验证

4.1 饱和约束一步最优控制仿真

与文献[1]相同,以A相电极为例,在式(25)上叠加如图3 所示的均值为0,方差为的随机噪声信号,并且将其作为对象仿真模型.

图3 随机噪声信号Fig.3 Random noise signal

其中,a1=−7.4099×10−5,b1=−2.4453×10−3.分别采用本文提出的饱和约束一步最优控制方法、文献[1]所描述的带输出补偿的PID 控制方法以及文献[21]所描述的数据驱动PID 控制方法,进行对比仿真实验.

与文献[1]相同,我们的控制目标为:

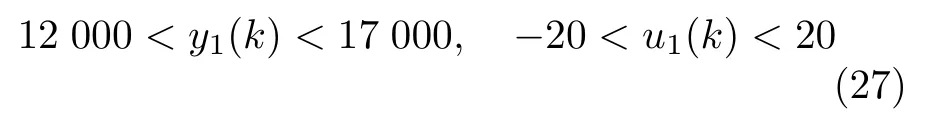
首先采用本文提出的饱和约束一步最优控制方法进行仿真实验.选择根据式(10)、式(16a)和式(16b)可以得到A 相电极电流饱和约束一步最优控制器的参数如下:

得到如图4 所示的A 相电极电流输出曲线.

图4 采用本文控制方法时A 相电极电流y1Fig.4 A-phase electrode current y1 using the control method in this paper

然后将文献[1]所述的带输出补偿的PID 控制方法应用到式(25),得到如图5 所示的A 相电极电流输出曲线.

图5 采用文献[1]控制方法时A 相电极电流y1Fig.5 A-phase electrode current y1 using the control method in [1]

最后采用文献[21]所述的数据驱动PID 控制方法进行仿真实验.针对式(25),设计如下控制器:其中,KP(k)、KI(k)和KD(k) 为 PID 的时变参数,利用CHR (Chien,Hrones and Reswick) PID 参数整定方法得到各参数初始值为:KP(0)=−1.181,KI(0)=1.012,KD(0)=−0.324,通过最速下降法在线校正PID 参数.将上述控制器应用到式(25),得到如图6 所示的A 相电极电流输出曲线.由图5和图6 可知,当采用文献[1]和文献[21]所述的控制方法时,虽然A 相电极电流能够围绕其设定值上下波动,同时也没有超出饱和约束范围,但是跟踪误差较大,由图4 可以看出,当采用本文所提出的控制方法时,跟踪误差明显降低.

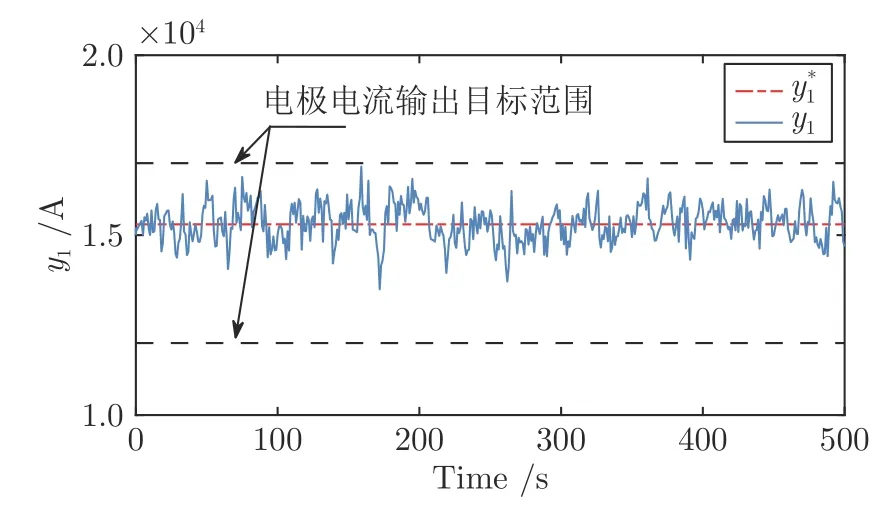
图6 采用文献[21]控制方法时A 相电极电流y1Fig.6 A-phase electrode current y1 using the control method in [21]

利用如下式(30a)和式(30b)所示的均方误差(Mean squared error,MSE)[22]和误差绝对值积分(Integrated absolute error,IAE)[1],对以上三种控制方法进行比较,得到如表2 所示的性能评价表.

根据表2 可以得到,当采用文献[1]的方法时,电极电流的 MSE 为 0.4502×106,IAE 为 0.2787×106,当采用文献[21]的方法时,电极电流的 MSE 为0.6631×106,IAE 为 0.2115×106,而当采用本文方法时,电极电流的 MSE 为 0.1294×106,IAE 为 0.0679×106.将本文方法与文献[1]方法对比,得到电极电流的MSE和 IAE 分别降低了 71.27% 和 75.64% ;将本文方法与文献[21]方法对比,得到电极电流的 MSE 和IAE分别降低了 80.48% 和 67.89% .该结果说明本文方法相较于文献[1]和文献[21]所提出的方法,能够较好地将电极电流控制在目标范围之内.

表2 采用文献[1]控制方法、文献[21]控制方法和本文控制方法时A 相电极电流 y1 的性能评价Table 2 Performance evaluating of A-phase electrode current y1 using the control method proposed in this paper and described in [1] and [21]

为了进一步体现本文所提方法的优越性,绘制如图7 和图8 所示的A 相电极电流误差经验概率分布图.从图7 和图8 可以看出,当采用本文所提出的控制方法时,电极电流误差超出控制目标(26)误差范围的概率更小.

图7 采用文献[21]控制方法时A 相电极电流误差概率分布Fig.7 Error probability distribution of A-phase electrode current using the control method in [21]

图8 采用本文控制方法时A 相电极电流误差概率分布Fig.8 Error probability distribution of A-phase electrode current using the control method in this paper

4.2 基于高阶干扰观测器的一步最优控制仿真

同第4.1 节所述,以A相电极为例,在式(25)上叠加如图3 所示的随机噪声信号和不可测干扰d1(k),并将其作为被控对象仿真模型:

为进行比较,首先采用第2 节不考虑不可测干扰的饱和约束一步最优控制方法进行仿真实验.运行时间从k=1到k=500,控制目标如式(26),控制器参数的选择如式(28),采用控制器式(8)进行仿真验证,得到如图9 所示的电极电流输出曲线,如图10 所示的控制器输出曲线.

图9 加入不可测干扰时A 相电极电流y1Fig.9 A-phase electrode current y1 when unmeasurable disturbance is introduced

图10 加入不可测干扰时控制器输出u1Fig.10 Controller output u1 when unmeasurable disturbance is introduced

利用式(30a)和式(30b)计算得到A 相电极电流的MSE=0.4970×106,IAE=0.0854×106,与第4.1 节没有加入干扰时A 相电极电流的 MSE 和IAE 值相比增大,因此,有必要对未知干扰进行处理.

首先,采用本文设计的高阶干扰观测器式(18)对干扰d1(k) 进行估计.根据定理3,选择高阶干扰观测器的阶次N=2,L0,L1和L2分别为:

则 1−z−1E(z−1)+z−1T(z−1)=0 的零点:

满足定理3 不等式零点在单位圆内的要求.其他控制器参数选择如式(28).

采用控制器式(24)进行仿真实验,得到如图11所示的A 相电极电流输出曲线,如图12 所示的控制器输出曲线,对未知干扰d1的估计如图13 所示.

图11 采用高阶干扰观测器控制时A 相电极电流y1Fig.11 A-phase electrode current y1 using the proposed high-order disturbance observer based controller

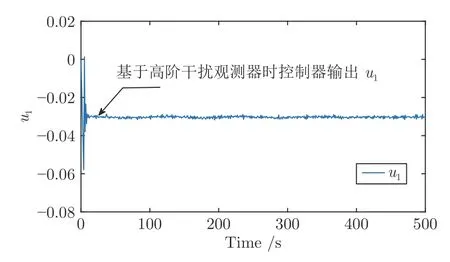
图12 采用高阶干扰观测器时控制器输出u1Fig.12 Controller output u1 using the proposed high-order disturbance observer based controller

图13 未知干扰 d1 的估计值Fig.13 Estimated value of unknown disturbance d1

为验证高阶干扰观测器具有较小的响应时间,我们做了与文献[23]所述方法的仿真对比实验,对比结果如图13 所示.图中d1是干扰的实际值,dˆ1,1是采用本文设计的高阶干扰观测器得到的估计值,dˆ1,2是采用文献[23]方法得到的估计值.由图13 可以看到,与采用文献[23]方法的估计值相对比,得到采用本文设计的高阶干扰观测器具有较小的响应时间.

为了与文献[24]所述的自抗扰输出反馈控制方法进行对比,首先将电熔镁砂熔炼过程输入输出模型(31)式转化成如下状态空间模型:

其中,z1(k)=y1(k),z2(k)=y1(k+1),并设计如下输出反馈控制器:

其中,φ(·) 是分段函数,与文献[24]中表达式相同.将上述算法应用到式(31),得到如图14 所示的A相电极电流输出曲线,如图15 所示的控制器输出曲线.

图14 采用文献[24]控制方法时A 相电极电流y1Fig.14 A-phase electrode current y1 using the control method in [24]

图15 采用文献[24]控制方法时控制器输出u1Fig.15 Controller output u1 using the method in [24]

采用性能评价指标MSE 和IAE 对加入不可测扰动时的系统进行性能评价,得到如表3 所示的性能评价表.

表3 采用文献[24]控制方法和本文控制方法时A 相电极电流 y1 的性能评价Table 3 Performance evaluating of A-phase electrode current y1 using the control method proposed in this paper and described in [24]

根据表3 可知,当加入不可测干扰后,根据第2 节提出的电极电流饱和约束一步最优控制方法,计算得到电极电流的 MSE 为 0.4970×106,IAE 为0.0854×106,当采用文献[24]所述的方法时,电极电流的 MSE 为0.5906×106,I AE 为0.2879×106,而当采用本文提出的控制方法时,电极电流的MSE 为 0.2951×106,IAE 为 0.0784×106.将本文提出的基于高阶干扰观测器的饱和约束一步最优控制方法与本文第2 节提出的饱和约束一步最优控制方法对比,计算得到电极电流的 MSE 和 IAE 分别降低了 40.62% 和 8.20%,将本文所提出的基于高阶干扰观测器的饱和约束一步最优控制方法与文献[24]所描述的控制方法对比,计算得到电极电流的MSE和 IAE 分别降低了 50.03% 和 72.77% .该结果说明本文方法相较于文献[24]所提出的方法,具有一定的优越性,能够较好地将电极电流控制在目标范围之内,并且设计的高阶干扰观测器可以较好地实现对未知干扰的估计.

5 结论

本文首先通过引入中间变量将复杂的电熔镁砂熔炼过程三相电极电流饱和约束控制问题简化为线性约束控制问题,提出了一种简化的电极电流饱和约束一步最优控制方法.然后,对熔炼过程可能存在的不可测干扰设计了高阶干扰观测器,提出了基于高阶干扰观测器的电熔镁砂熔炼过程简化控制算法.最后通过理论分析和仿真对比实验验证了本文所提方法的有效性和优越性.由于本文所提方法针对的是电熔镁砂的单批加料过程,在接下来的研究工作中,我们会针对多批加料过程考虑如何设计有效的控制器使电极电流跟踪其设定值.