碳化硅中点缺陷对热传导性能影响的分子动力学研究*

王甫 周毅 高士鑫 段振刚 孙志鹏 汪俊 邹宇 付宝勤†

1)(四川大学原子核科学技术研究所,辐射物理及技术教育部重点实验室,成都 610064)

2)(中国核动力研究设计院,核反应堆系统设计技术重点实验室,成都 610200)

碳化硅(SiC)由于性能优异,已广泛应用于核技术领域.在辐照环境下,载能入射粒子可使材料中的原子偏离晶体格点位置,进而产生过饱和的空位、间隙原子、错位原子等点缺陷,这些缺陷将改变材料的热物性能,劣化材料的服役性能.因此,本文利用平衡分子动力学方法(Green-Kubo 方法)采用Tersoff型势函数研究了点缺陷对立方碳化硅(β-SiC 或 3C-SiC)热传导性能的影响规律.研究过程中考虑的点缺陷包括:Si 间隙原子(SiI)、Si 空位(SiV)、Si 错位原子(SiC)、C 间隙原子(CI)、C 空位(CV)和C 错位原子(CSi).研究结果表明,热导率(λ)随点缺陷浓度(c)的增加而减小.在研究的点缺陷浓度范围(点缺陷与格点的比例范围为0.2%—1.6%),额外热阻率(ΔR=Rdefect—Rperfect,R=1/λ,Rdefect 为含缺陷材料的热阻率,Rperfect 为不含缺陷材料的热阻率)与点缺陷的浓度呈线性关系,其斜率为热阻率系数.研究表明:空位和间隙原子的热阻率系数高于错位原子的热阻率系数;高温下点缺陷的热阻率系数高于低温下点缺陷的热阻率系数;Si 空位和Si 间隙原子的热阻率系数高于C 空位和C 间隙原子的热阻率系数.这些结果有助于预测及调控辐照条件下碳化硅的热传导性能.

1 引言

碳化硅(SiC)因具有优异的性能,如抗辐照能力强、化学稳定性好、热导率高[1]等,在核技术领域备受关注[2-4].由于SiC 堆垛层错的形成能低[5],所以具有多型体现象,即成分相同,但构型和物理性质有差异[6].目前,已经发现的SiC 多型体有250 多种[7].其中,受关注比较多的是立方结构(β-SiC 或3C-SiC),六方结构(如4H-SiC 和6H-SiC).在高温气冷堆[8]中,3C-SiC 作为TRISO (tristructural-isotropic)型包覆燃料颗粒(简称TRISO 颗粒)中的包覆层[9],可阻挡裂变产物的释放,且可高效导出核芯的热能,避免堆芯温度过高.然而,在辐照环境下,载能入射粒子(如中子和裂变碎片等)可使材料中的原子偏离晶体格点位置,引起离位损伤,进而产生过饱和的空位、间隙原子、错位原子等点缺陷.3C-SiC 中的基本点缺陷类型包括:Si 间隙原子(SiI)、Si 空位(SiV)、Si 错位原子(SiC)、C 间隙原子(CI)、C 空位(CV)和C 错位原子(CSi),这些缺陷是构成复合缺陷的基本单元.Katoh 等[10]研究了中子辐照下3C-SiC 的微观结构变化,结果表明,在相对较低的温度(≤800 ℃)下,辐照后材料里的缺陷主要为点缺陷及小间隙团簇.Devanathan 等[11]和Ran 等[12]基于分子动力学研究表明,基本撞击原子辐照产生的剩余点缺陷主要为Frenkel 对和错位原子.这些缺陷会影响材料的热物性能,在辐照条件下,SiC 材料的热导率会降低[13].这可能会导致堆芯过热进而造成TRISO 颗粒失效,影响反应堆的安全运行.因而研究点缺陷对3C-SiC 热传导性能的影响规律有重要意义.

在实验中获得单种点缺陷类型的试样和准确调控缺陷浓度是极其困难的[14],因而有必要借助计算机模拟技术来研究缺陷对材料热导率的影响.分子动力学(molecular dynamics,MD)是一种合适研究晶体缺陷对热导率影响的方法.只需针对待研究体系建立适当的势函数,就可以模拟其主要的热力学性质和动力学性质.分子动力学计算材料声子热导率的方法主要包括平衡分子动力学(equilibrium molecular dynamics,EMD)和非平衡分子动力学(non-equilibrium molecular dynamics,NEMD)两种方法[15,16].Crocombette 等[17]利用NEMD 方法研究了辐照对β-SiC 热导率的影响.相似的方法被用来计算SiC 纳米管、纳米线的热导率[18].这些研究表明了分子动力学研究SiC 中点缺陷对热传导性能影响的可行性.然而NEMD 方法的不足之处是存在明显的尺寸效应[19],计算过程中存在较大的温度梯度引起非线性的人为现象,且仅能获得给定热流方向的热导率.EMD 方法避免了NEMD的主要不足,在计算过程中系统长时间保持恒定温度,始终处于线性响应状态.因而本文采用EMD方法研究点缺陷对3C-SiC 热导率的影响规律.研究表明,含有点缺陷的SiC 材料的热阻率与点缺陷的浓度(考虑的点缺陷与格点比范围为0.2%—1.6%)呈线性关系,对应的斜率为热阻率系数;空位和间隙原子的热阻率系数高于错位原子的热阻率系数;高温下点缺陷的热阻率系数高于低温下点缺陷的热阻率系数;Si 空位和Si 间隙原子的热阻率系数高于C 空位和C 间隙原子的热阻率系数.

本文余下部分组织如下:第2 节给出热导率计算所用的方法和具体的模拟细节;第3 节结果与讨论,包括热流密度的时间自相关函数收敛性分析和不同点缺陷及其浓度对热传导性能的影响;最后是全文的结论.

2 方法

2.1 平衡分子动力学

在分子模拟中,计算热导率的EMD 方法一般是指利用Green-Kubo 公式[20]计算热流密度的时间自相关函数(HFACF)来求解体系声子热导率的方法.计算SiC 热导率(λ)的Green-Kubo 公式为

式中kB为玻尔兹曼常数;T为系统温度;V表示β-SiC 超胞体积;J为系统瞬时微观热流密度;〈·〉表示HFACF 的系综统计平均,在MD 计算过程中通过时间平均来计算系综平均.微观热流密度的计算公式为

式中t为时间,εi表示原子i能量,vi表示原子i的速度,Si表示原子i的virial 应力.

2.2 模拟细节

采用LAMMPS 软件包进行MD 模拟[21].采用Tersoff型[22]势函数[23]描述SiC 中原子间的相互作用,该势函数可较好地描述3C-SiC 的点缺陷相对稳定性和弹性性能及热学性能.在计算过程中考虑了不同尺寸的超胞,包括4a×4a×4a(512),5a×5a×5a(1000),6a×6a×6a(1728)和7a×7a×7a(2744),其中a表示立方SiC 结构胞的晶胞参数,括号中的数字表示相应尺寸完美超胞中的原子数,超胞的3 个轴取向分别为[100],[010]和[001].为了在超胞中引入点缺陷,通过随机删除一定数量的C(Si)格点原子构建一定浓度的C(Si)空位,通过随机选择一定数量的Si(C)格点改变为C(Si)原子构成C(Si)错位原子,通过在超胞的随机位置引入一定数量的C(Si)原子构成C(Si)间隙原子.所有超胞x,y和z方向均采用周期性边界条件.在MD 运行前,先对含有点缺陷的超胞进行原子位置最优化处理,采用共轭梯度算法,使各原子优化至局部最稳定位置.MD 运行的时间步长是0.3 fs,经过测试,发现这个时间步长足够小,具有足够精度获得可靠的计算结果.针对优化后的超胞,对原子进行热化以接近目标温度,本文考虑的温度包括600 和1500 K.然后通过Nose-Hoover调温技术[24]和Parrinello-Rahman 调压技术[25]产生等温等压系综(NPT 系综),使用时间可逆速度Verlet 算法[26]运行约160000 步(48 ps).正式采样时改为微正则系综(NVE 系综)运行MD,每隔20 步(即6 fs)取当前的瞬态构型(包括当前的超胞轴取向、各个原子的坐标、速度和受力)以计算当前的瞬间微观热流密度(如(2)式所述),然后通过时间平均来获得超胞的HFACF,最后根据(1)式对HFACF 进行积分计算热导率.MD 计算的总步数至少32000000 步(9600 ps),关联时间至少大于15 ps,以保证计算的收敛和可靠性.另外为了防止计算的偶然性,又分别进行了至少20 次独立的计算,以获得热导率的统计平均值.

3 结果与讨论

3.1 热流密度的时间自相关函数(HFACF)

基于瞬间构型提炼超胞的体积和各原子的动能、势能、Virial 应力和速度等物理量,体系的微观热流密度可根据(2)式获得,热流密度随时间的变化如图1(a)所示,这里以完美超胞(6a×6a×6a)在1500 K 时的模拟结果为例进行分析,可以发现超胞不同方向的微观热流密度(Jx,Jy和Jz)并无明显差别,这是由于3C-SiC 的3 个轴向是完全等效的.微观热流密度数值均在0 eV/(ps·Å2)上下变动,变动范围约为—0.2—0.2 eV/(ps·Å2).该超胞在1500 K 时HFACF 与时间的关系如图1(b)所示,可以看到HFACF 在初始时变化较大,在时间达到10 ps 后减小至接近为0,因此可以认为这时热流密度不再时间相关或相关较小,因而如前文所述,关联时间设置为15 ps.因此,可用有限时间的MD 模拟,通过HFACF 与时间的关系,运用(1)式对HFACF 进行一定时间的积分可获得热导率.从图1(b)还可以发现,超胞的取向对HFACF 无影响,同样是由于3C-SiC 的高对称性.除了关联时间,使用Green-Kubo 公式计算体系的热导率时,还需足够长的时间进行累积平均,相当于系综平均的时间,本文要求正式采样的MD 运行总时间不少于9600 ps,可保证计算结果的收敛.本文测试了不同尺寸完美超胞的热导率,如图2 所示.可以看出,在尺寸为6a×6a×6a时热导率收敛至67.8 W/mK(1500 K),是与实验值(62.6—68.6 W/mK[27])接近.而600 K 时完美超胞的热导率为325 W/mK,若进行量子修正[28]也与实验值接近.

图1 (a)微观热流密度(J)随时间的变化关系;(b)微观热流密度的时间自相关函数(HFACF)随时间的变化关系.温度为1500 K,完美超胞的尺寸为6a×6a×6aFig.1.(a)Relationship of microscopic heat flux (J)with time;(b)relationship of heat flux autocorrelation function(HFACF)with time.The temperature is 1500 K,the size of the perfect supercell is 6a×6a×6a.

图2 尺寸对热导率的影响Fig.2.Effect of size on the thermal conductivity.

3.2 点缺陷对热导率的影响

如前文所述,SiC 材料在辐照环境下服役,将受到中子和裂变碎片等载能粒子轰击,引起材料中格点原子离位,进而产生过饱和的空位、间隙原子、错位原子等点缺陷.点缺陷的种类和浓度受到载能粒子(能量、通量和剂量等)、SiC 材料状态(结构)和其他服役条件(温度和压力等)等因素的影响[10-12].为了研究点缺陷类型及其浓度对3CSiC 热传导性能的影响,本文针对不同的点缺陷类型,构建了不同点缺陷浓度的超胞.根据前文的参数设置及计算流程,计算了不同类型点缺陷在不同浓度下的热导率,结果如图3 所示.可以发现随着点缺陷浓度的增加,SiC 材料的热导率(λ)下降.当然不同类型的点缺陷,对应超胞的热导率数值不同,这是由不同类型点缺陷对声子的散射行为的差异造成的.另外从图3 还可以发现,错位原子(尤其是CSi)对应超胞的热导率较大,即对声子的散射较小;而Si型点缺陷(尤其是SiI)对应超胞的热导率较小,即对声子的散射较大.对比图3(a)和图3(b)可以发现,温度不影响上述点缺陷类型及浓度与热导率的主要规律,仅影响热导率数值的大小.另外研究过程中还发现,间隙原子构型(对于本文使用的Tersoff 势函数,C 间隙的稳定构型为C+-C〈100〉,Si 间隙的最稳定构型为Si+-C〈100〉)将影响超胞的热传导行为,dumbbell 间隙轴向(即其中一个〈100〉取向)的热导率要小于横向(即另外两个〈100〉取向)的热导率.

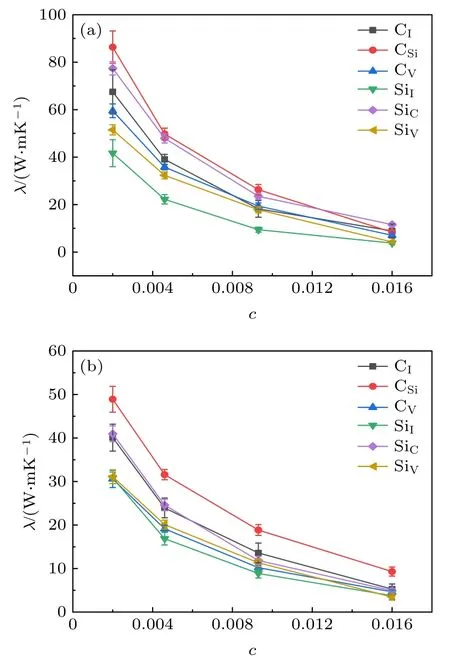
图3 含有点缺陷的SiC 超胞热导率(λ)与点缺陷浓度(c,相当于点缺陷与格点的比例)的关系 (a)600 K;(b)1500 KFig.3.Relationship between the thermal conductivity (λ)of SiC supercells containing point defects and the concentration of point defects (c,equivalent to the ratio of point defects to lattice points):(a)600 K;(b)1500 K.

SiC 热传导的主要载体是声子,在温度高的区域晶格振动具有更大的振幅和更多的模式,即声子数更多,这些声子将传递至低温区域,然而声子间存在相互作用,传递过程将发生碰撞,在材料中引入点缺陷,也将影响声子的传递,声子会与缺陷发生碰撞,降低声子寿命.根据声子的玻尔兹曼输运理论[29],(其中Cμ为对应声子模μ比热容,vαμ是α方向声子模μ的群速度,τμ为声子模μ的驰豫时间),晶格热导率主要取决于声子的比热容、群速度和寿命(驰豫时间).点缺陷降低了声子寿命,从而使得热导率减小.也就是说引入的点缺陷将增加材料的热阻率(R=1/λ),我们将点缺陷引起的热阻率增加部分称为额外热阻率(ΔR=Rdefect—Rperfect,其中Rdefect为含有点缺陷材料的热阻率,Rperfect为不含点缺陷材料的热阻率),显然额外热阻率受到点缺陷浓度的影响,点缺陷的浓度越高,额外热阻率越大,在较小的浓度范围内,可以认为额外热阻率随点缺陷浓度的升高而线性升高.如图4 所示,额外热阻率与点缺陷浓度确实呈现较好的线性关系,该结果与Crocombette和Proville[30]的结论一致.那么图4 中ΔR-c关系可用以下公式来描述:

式中l定义为热阻率系数;ΔR0为拟合系数,相当于点缺陷浓度为0 时的额外热阻率,该值应该为0,事实上,拟合结果发现ΔR0基本上接近于0.另外应该说明的是,这种ΔR-c的线性关系仅存在于较低的浓度范围内,对于高的点缺陷浓度,点缺陷之间将存在相互作用,甚至相互反应生成复杂的点缺陷团簇,进而影响点缺陷对声子的散射过程.

显然根据(3)式,在确定了某温度下各类型点缺陷的热阻率系数后,可估算低点缺陷浓度下SiC 材料的热导率,预测计算的公式为

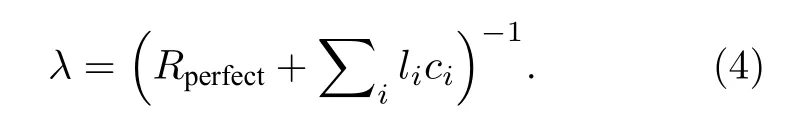
(4)式假定了各种类型点缺陷的热阻率系数是相互独立的,显然仅在低点缺陷浓度下成立.另外该预测公式未考虑实际材料中位错、晶界、层错和相界等缺陷结构的影响.

根据图4 中的拟合曲线可得到在温度为600和1500 K 条件下各种点缺陷的热阻率系数,结果如图5 所示.可以看出,空位和间隙型点缺陷引起的热阻率系数一般比错位型点缺陷的热阻率系数高;高温下点缺陷的热阻率系数一般比低温下点缺陷的热阻率系数高;Si 类型点缺陷(Si 空位和Si间隙)引起的热阻率系数一般比C 类型(C 空位和C 间隙)的热阻率系数高.这是因为在无机非金属中,热传导的主要载体是声子,即晶格振动的能量量子[31].因此,热阻(L/λ,L为热流方向材料长度)主要是由声子之间的相互作用和晶体缺陷散射声子引起的[32].空位或间隙引起了最大的质量差和半径差,这将导致更强的点缺陷-声子散射[33,34],从而导致更高的热阻率系数.

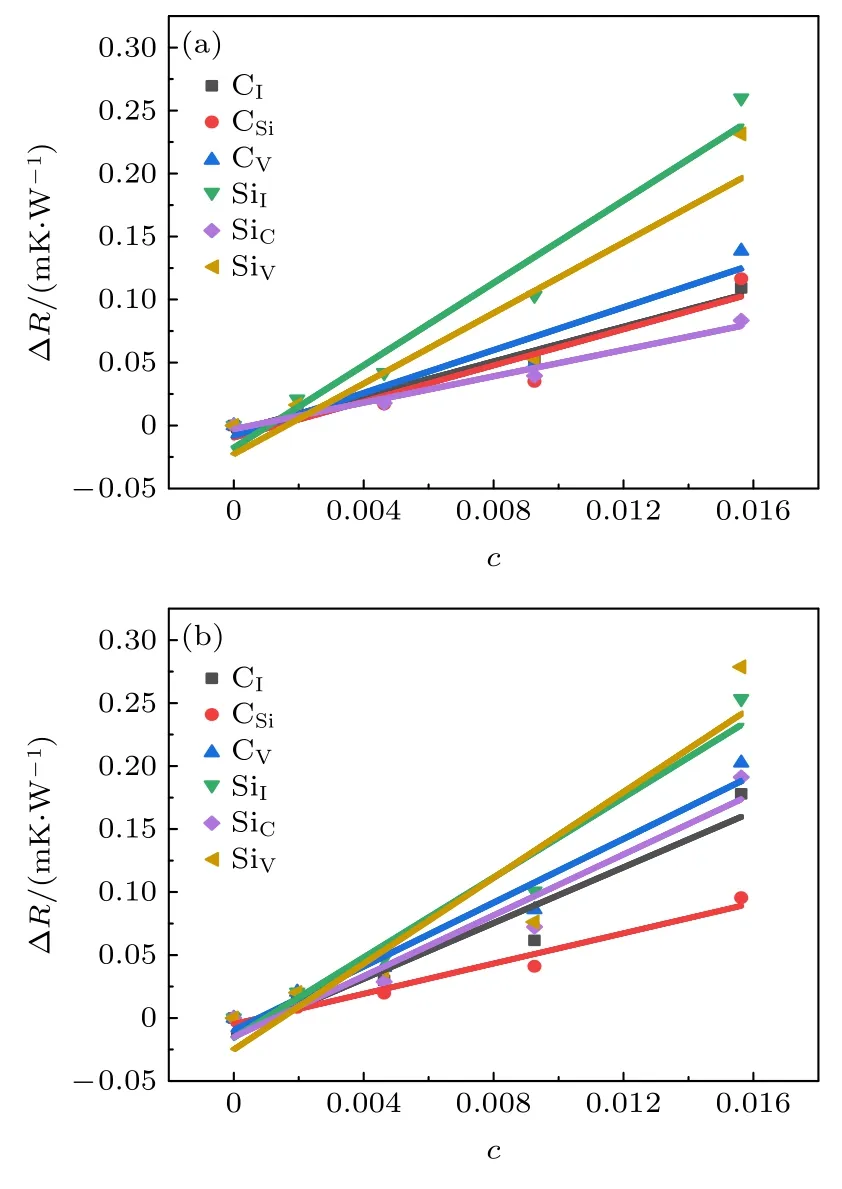
图4 含有点缺陷的SiC 超胞的额外热阻率(ΔR)与点缺陷浓度(c,相当于点缺陷与格点的比例)的关系 (a)600 K;(b)1500 KFig.4.Relationship between the excess thermal resistance(ΔR)of SiC supercells containing point defects and the concentration of point defects (c,equivalent to the ratio of point defects to lattice points):(a)600 K;(b)1500 K.

图5 各种点缺陷不同温度下的热阻率系数l (单位为mK/W)Fig.5.Thermal resistivity coefficient l (in mK/W)of various point defects at different temperatures.

4 结论

本文利用EMD 方法(Green-Kubo 公式),研究了6 种点缺陷(Si 间隙原子(SiI)、Si 空位(SiV)、Si 错位原子(SiC)、C 间隙原子(CI)、C 空位(CV)和C 错位原子(CSi))在不同浓度(点缺陷与格点比为0.2%—1.6%)下对立方碳化硅(β-SiC 或3CSiC)声子热导率的影响规律.研究发现热导率(λ)随点缺陷浓度(c)的增加而减小.在研究的点缺陷浓度范围内,额外热阻率(即点缺陷引起的热阻率的增加值)与点缺陷的浓度呈线性关系,间隙原子构型取向使热传导行为呈现各向异性.以热阻率系数作为衡量点缺陷对材料热阻率(热导率)影响程度大小的影响因子,空位和间隙引起的热阻率系数高于错位原子的热阻率系数;高温下点缺陷的热阻率系数高于低温下点缺陷的热阻率系数;Si 空位和Si 间隙比C 空位和C 间隙引起更高热阻率系数.这些结果可为预测辐照条件下SiC 热导率以及调控SiC 热传导性能提供参考.