粗糙面上粒子层矢量辐射传输方程的二阶迭代解法*

姚海 何姿† 丁大志 陈如山 党训旺 陈勇

1)(南京理工大学电子工程与光电技术学院,南京 210018)

2)(电磁散射重点实验室,北京 100089)

为了探究典型粗糙面上随机粒子层中能量传输的多次散射机制,提出了一种基于矢量辐射传输方程的建模二阶计算方法.该建模方法将建模场景(粗糙面上粒子层)在高度维(Z 轴)划分为多个传输散射层,基于矢量辐射传输理论中的一阶迭代散射解,利用典型粗糙面的半经验半解析方法,求解出整个场景的二阶迭代散射解.同时,研究粒子层能量在粒子与粒子间的多次散射机制,以及粒子与地表粗糙面间的多次散射机制.数值结果表明,该二阶迭代解法相较于矢量辐射传输方程的一阶迭代散射解,能够更完整地探究互作用的散射特性,且可从能量传输角度解译建模场景中物体间的相干作用,从而可用于植被地物环境下的多次散射机制的解析以及散射系数变化趋势的预估.

1 引言

与地物电磁散射特性有关的研究,在遥感、探测、反隐身等领域具有重要的应用价值.地物对象包括各种地形地貌,如雪地、土壤、沙漠、海面等,以及大自然中的各种植被,如草地、树木、庄稼等.地物研究的种类之多、范围之广,足以可见研究地物电磁散射特性的强烈需求和重要性.

对于典型地表植被散射的建模,在Ulaby 等[1]提出的密歇根森林植被散射模型(MIMICS)的基础上,文献[2-5]等基于矢量辐射传输(vector radiative transfer,VRT)方程发展了粒子层散射矢量辐射传输模型,采用随机取向的粒子模拟树冠和树干[6-9],求解VRT 方程的一阶解.同时,引入由Fung 等[10]提出基于积分方程方法的随机粗糙表面散射,可用于求解出包含粗糙面散射的Mueller矩阵解,模拟出非球型粒子体散射和粗糙面的散射耦合,建立粗糙面上混杂非球型粒子散射模型[11-13].除此之外,对于非均匀散射层中VRT方程多次散射求解的问题,也有相关的讨论[14,15],但是,对于包含粗糙面散射和非球型粒子体的多次散射耦合的VRT 二阶Mueller 矩阵解,目前暂没有详细的推导和讨论.

VRT 方程是一种半解析建模方法,在分析讨论建模对象的过程中,结合物体参数和环境特性在实际情况中的复杂性,用解析公式加上由大量实际的实验数据拟合的经验公式,来对背景环境进行建模.VRT 描述了电磁波在传输的过程中由于环境背景的散射、吸收、衰减以及增益的影响,使电磁波能量发生相应的变化,可用一定的微积分方程来描述.通常,对典型植被地面环境的研究分析,可将其建模成粗糙面上混杂粒子层,使用VRT 半解析方法进行数值仿真[16-18].

对于粗糙面上粒子层的模型,本文在VRT 一阶迭代解的基础上,求解出VRT 二阶迭代解的表达式,探究粒子层中粒子间、粒子与粗糙面间的多次散射作用,分析粒子层整体的后向散射系数随入射角、占空比的变化规律,以及二阶迭代解的数值作用.

2 VRT 二阶散射的迭代解方法

2.1 VRT 方程及一阶迭代解

如图1 所示,将典型地物场景的建模在垂直方向(Z轴)分为两层,上层为模拟离散地物模型的粒子层,在层厚d∈(-d1,0)均匀分布随机粒子模型.下层d=-d1处为模拟随机粗糙面的地表层.当电磁波在粒子层和地表层之间发生传播时,电磁波的能量随着电磁波传播距离的增大而改变,此时电磁波的强度变化可通过VRT 方程方法来分析.一般情况下,VRT 方程表示为

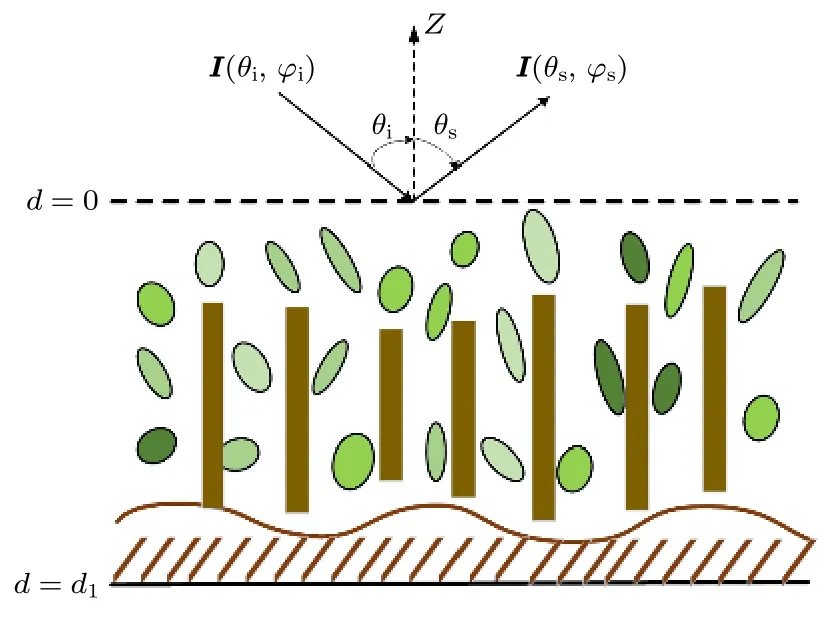
图1 粗糙面上粒子层模型示意图,图中为层厚为d1 的粒子层,最下层为随机粗糙面模型,绿色部分为粒子层中椭球粒子模型,深色部分为圆柱粒子模型Fig.1.Particle layer model on rough surface.The figure shows the particle layer with layer thickness of d1,the bottom layer is the random rough surface model,the green parts is the ellipsoid particle model in the particle layer,and the dark parts is the cylinder particle model.

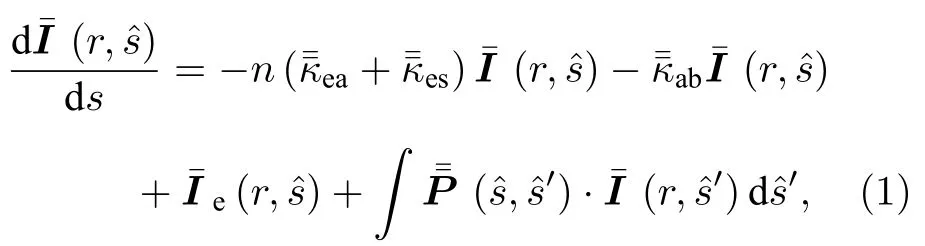
为解决粗糙面上粒子层的一维VRT 问题,将(1)式改写为关于z方向的一维偏微分方程,即有坐标变化:

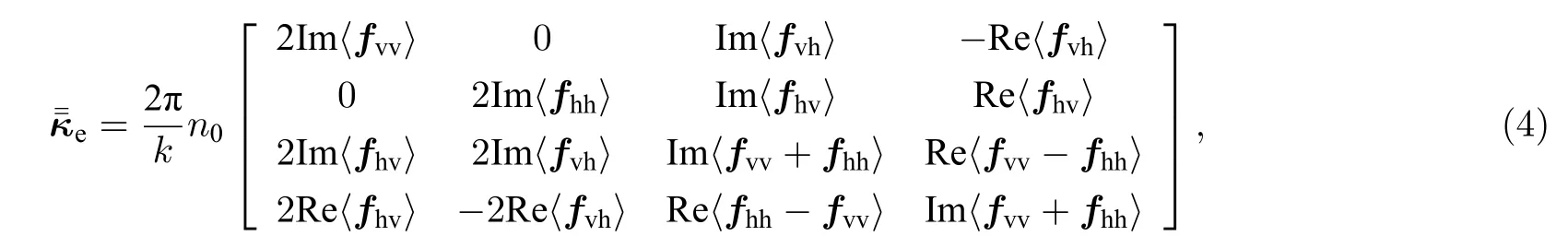
其中,k为波数,n0为单位体积粒子数,fvv为粒子前向散射矩阵.

微积分方程通解为

其中A为迭代相关系数,等式右侧第二项为迭代求解需要更新的部分.(5)式可求解出(3)式的通解,即VRT 上行波和下行波迭代解的一般表达式:

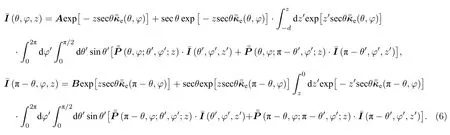
通过边界条件求A和B,代入边界条件:

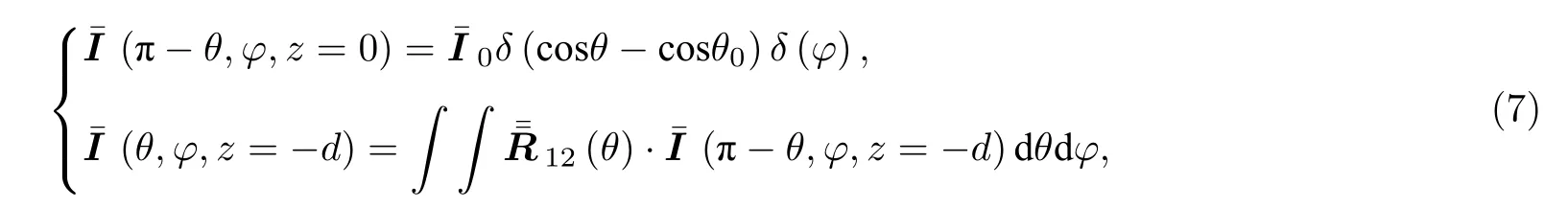
VRT 边界迭代关系为

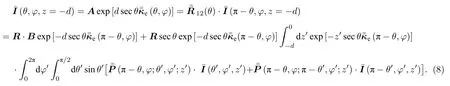
可求得迭代系数的一般表达式为

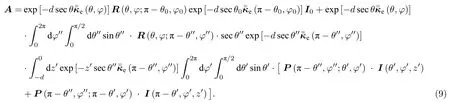
VRT 一阶解忽略电磁波多次散射的作用,即忽略迭代更新部分置零,求解迭代系数A,推导VRT 一阶散射迭代解[2],本文直接给出建模环境任意位置中VRT 一阶散射解的一维表达式,上行波、下行波的具体表达式分别为

2.2 VRT 方程的二阶迭代解

在建立的粗糙面上方随机粒子层模型中,对于所建立的一维VRT 方程,可设置粒子层上下边界条件为[2]

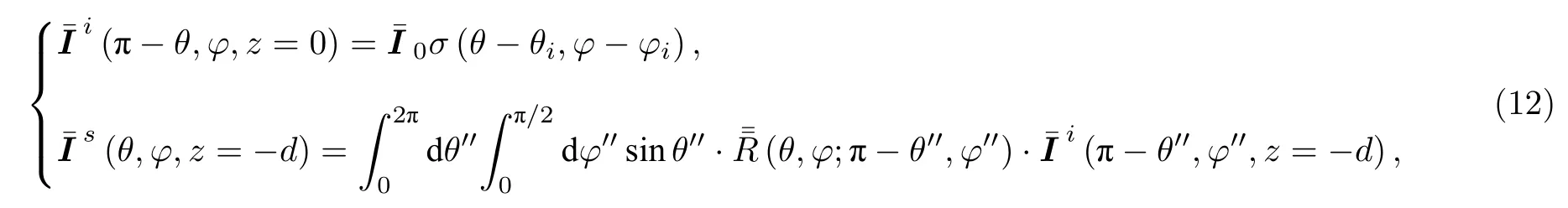
VRT 散射迭代二阶解推导过程如下.

步骤1给出在粒子层中,VRT 二阶迭代解的通解,其中上行波和下行波分别为

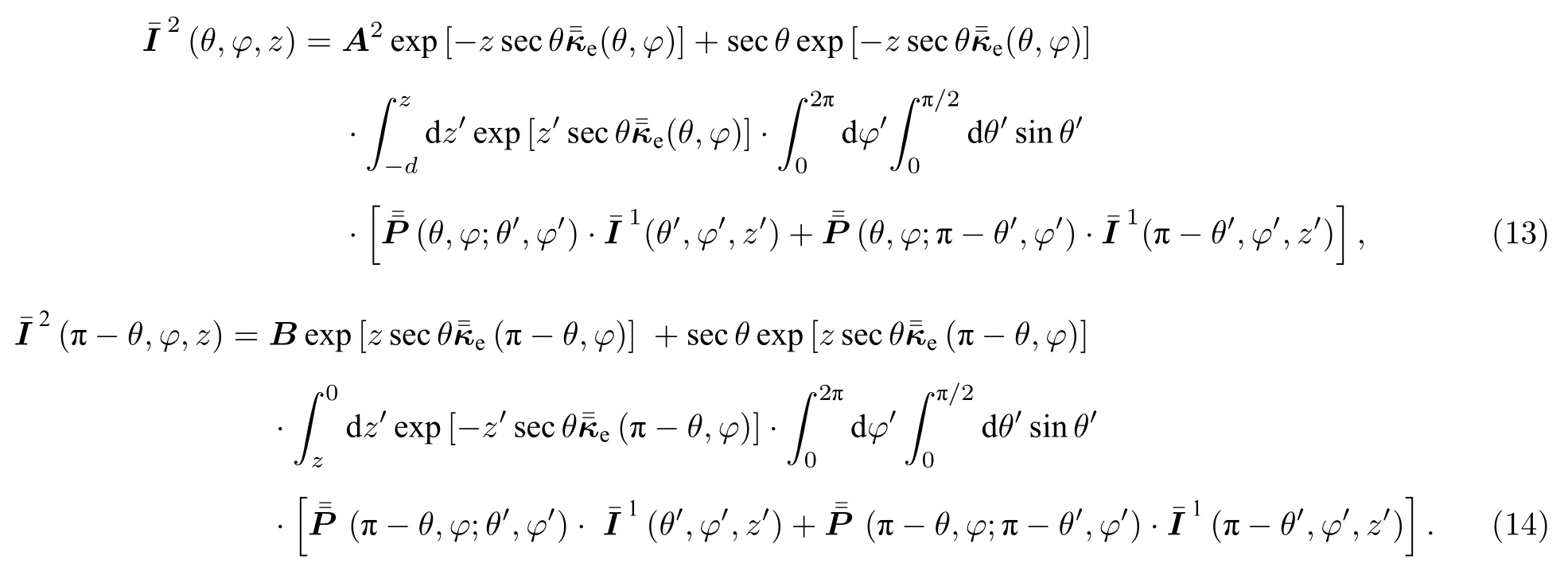
步骤2给出的VRT 一阶解,并作为迭代的散射源,即(10)式和(11)式,一阶解在任意位置的具体表达式,代入二阶解通解公式中,得到代入新的散射源后的二阶解通解.

步骤3将(13)式和(14)式联立VRT 边界条件(7),更新得到二阶系数A2的表达式,如(15)式.将VRT 一阶解也代入A2,得到A2完整形式,如(16)式:

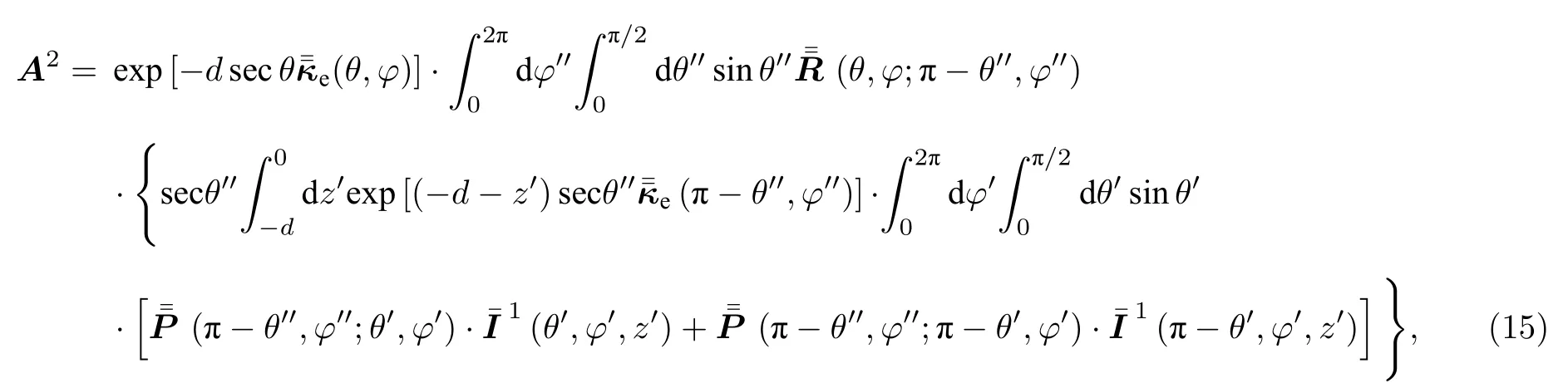
步骤4将A2代入VRT 二阶解通解,可得粒子层任意位置VRT 二阶迭代的多次散射解.令VRT 二阶解上行波z=0,即为电磁波离开粒子层(最上层表面)的散射强度:

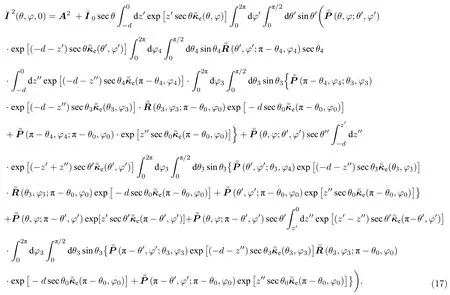
3 VRT 二阶迭代解的Mueller 矩阵

如图2,电磁波在粒子层中传输,通过不同的散射过程,最终从粒子层传输出去.VRT 方程反映了电磁波能量的变化,从物理意义的角度,将VRT 迭代解表达式分解为多次散射项,加入描述电磁波与目标之间作用的Mueller 矩阵,最终形式表示:

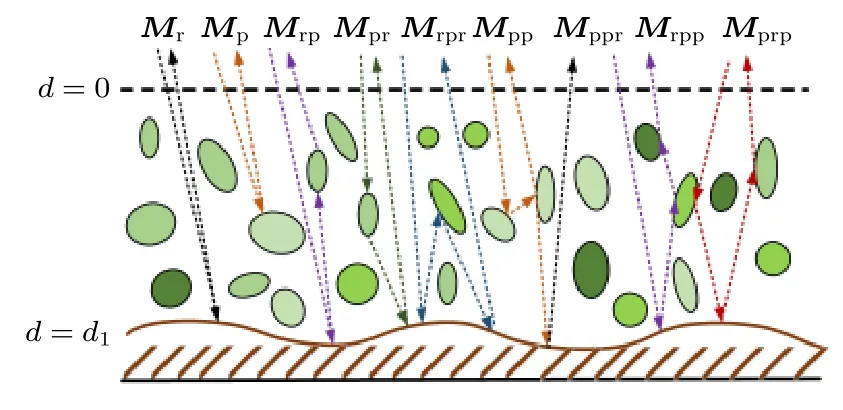
图2 VRT 方程各项散射机制示意图.图中最上层为粗糙面模型,绿色部分表示粒子层随机分布的粒子模型,粒子层层厚为d1,Mi 为VRT 方程不同散射机制Muller 矩阵解Fig.2.Various scattering mechanisms of VRT equation.In the figure,the top layer is the rough surface model,and the green parts represent the particle model with random distribution of particle layers.The thickness of particle layers is d1,and Mi is the solution of Muller matrix with different scattering mechanism of VRT equation.

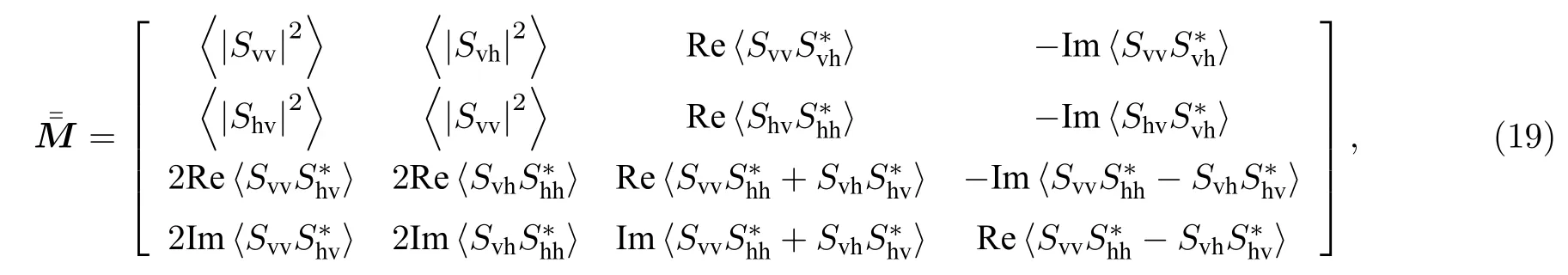
其中,1)当S为粒子的散射矩阵时,可表示为粒子的相函数矩阵形式,且,n0为单位体积内粒子数.

2)当S为下垫粗糙面的散射矩阵时,可表示为粗糙面的相函数矩阵形式,即.

当Mueller 矩阵描述电磁波在环境中传播的能量变化时,Mueller 矩阵解可表示为VRT 多次迭代解之和:

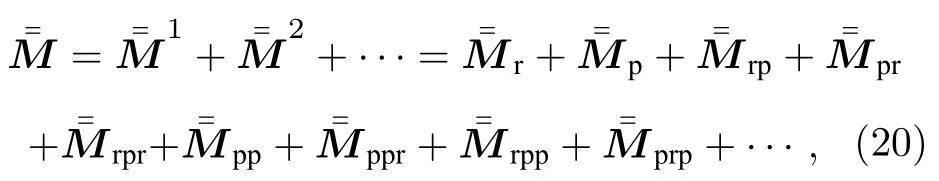
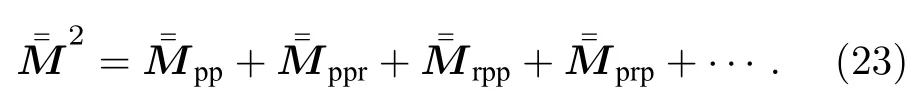
二阶解的多次散射项,从实际散射方式划可分为4 种,其详细散射过程参考本节后面内容.对于粒子层存在的其他更多次散射项,散射机制具体表达式也可得到,由于其数值对于求解的VRT 方程的效果极小,无实际意义,故不再讨论和分析.

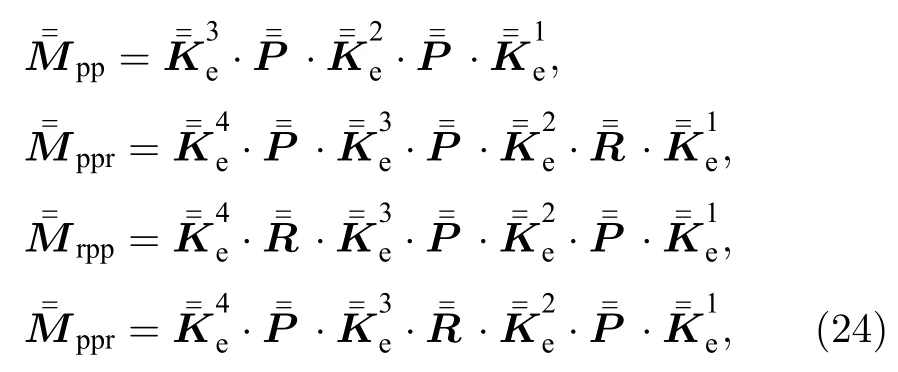
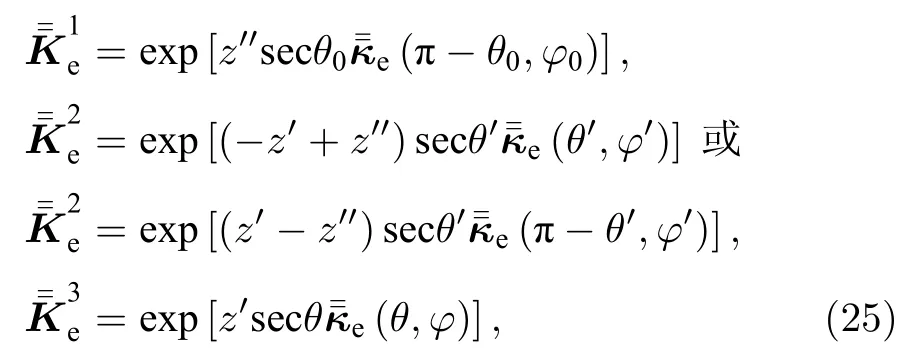
3.1 粒子-粒子的二次散射

如图3(a)所示,该散射过程代表电磁波首先进入粒子层,然后电磁波经过两次粒子散射作用,最终从粒子层散射出去.其数学表达式为

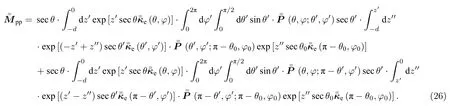
3.2 粒子-粒子-粗糙面之间的三次散射机制

如图3(b)所示,该散射过程代表电磁波首先进入粒子层,然后电磁波首先经过了两次粒子散射作用,又经过一次粗糙面散射作用,最终从粒子层散射出去.其数学表达式为

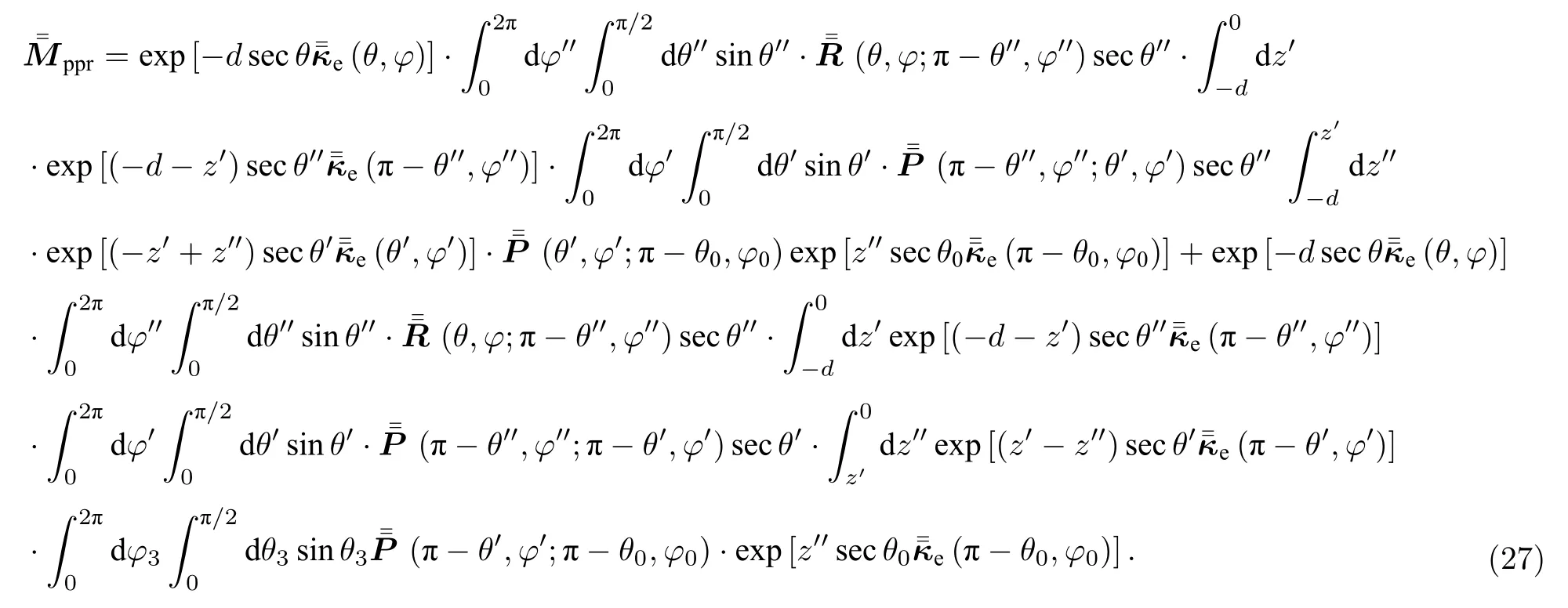
3.3 粗糙面-粒子-粒子的三次散射机制

如图3(c)所示,该散射过程代表电磁波首先进入粒子层,然后电磁波经过了一次地表粗糙面的散射作用,又经过了两次粒子散射作用,最终从粒子层散射出去.其数学表达式为

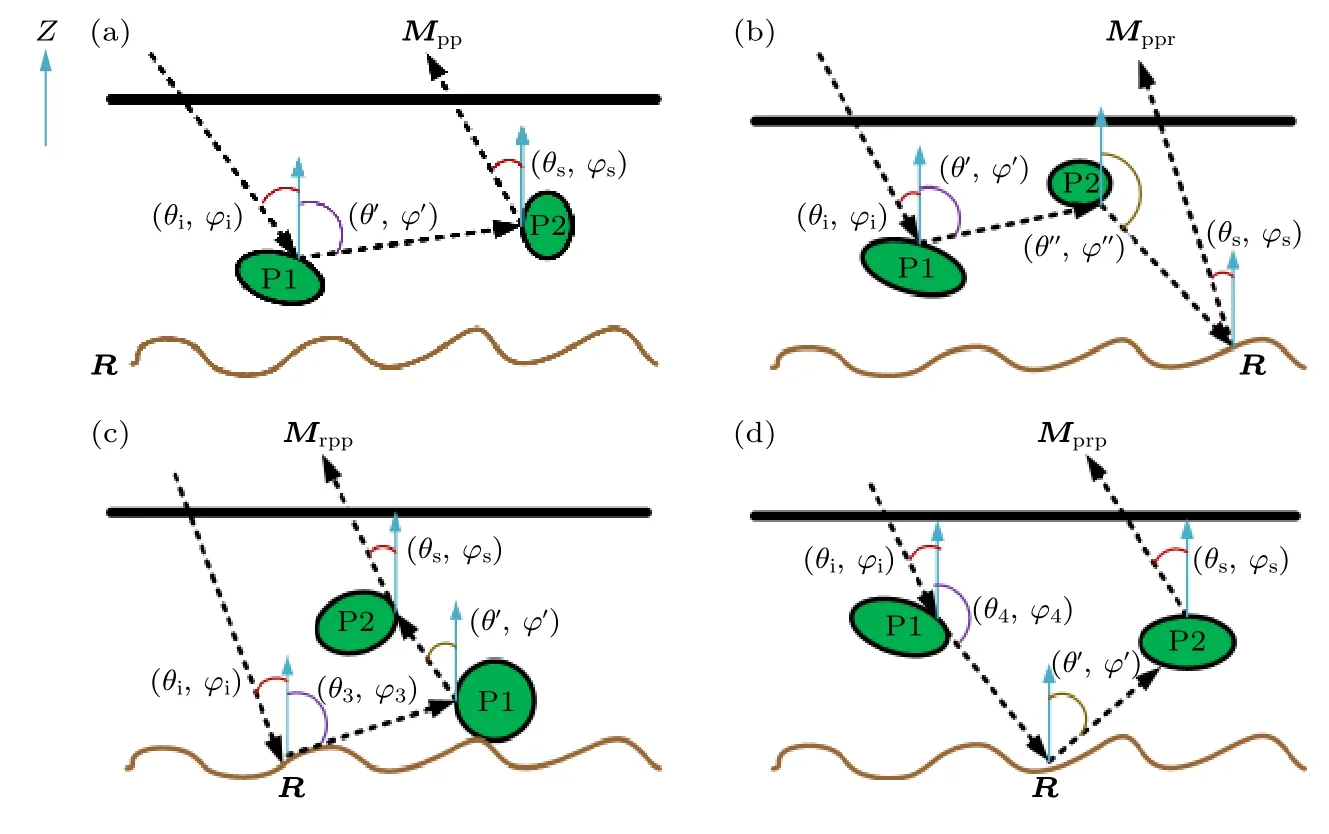
图3 粒子层多次散射过程示意图 (a)(粒子-粒子)二次散射机制示意图;(b)(粒子-粒子-粗糙面)三次散射机制示意图;(c)(粗糙面-粒子-粒子)三次散射机制示意图;(d)(粒子-粗糙面-粒子)三次散射机制示意图Fig.3.Diagram of multiple scattering process of particle layer:(a)(Particle-particle)secondary scattering mechanism;(b)(particleparticle-rough surface)third-order scattering mechanism;(c)(rough surface-particle-particle)third-order scattering mechanism;(d)(particle-rough surface-particle)third-order scattering mechanism.

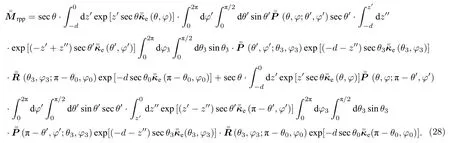
3.4 粒子-粗糙面-粒子的三次散射机制

如图3(d)所示,该散射过程代表电磁波首先进入粒子层,然后电磁波经过一次粒子散射作用,再经过地表粗糙面的散射作用,又经过一次粒子散射作用,最终从粒子层散射出去.其数学表达式为

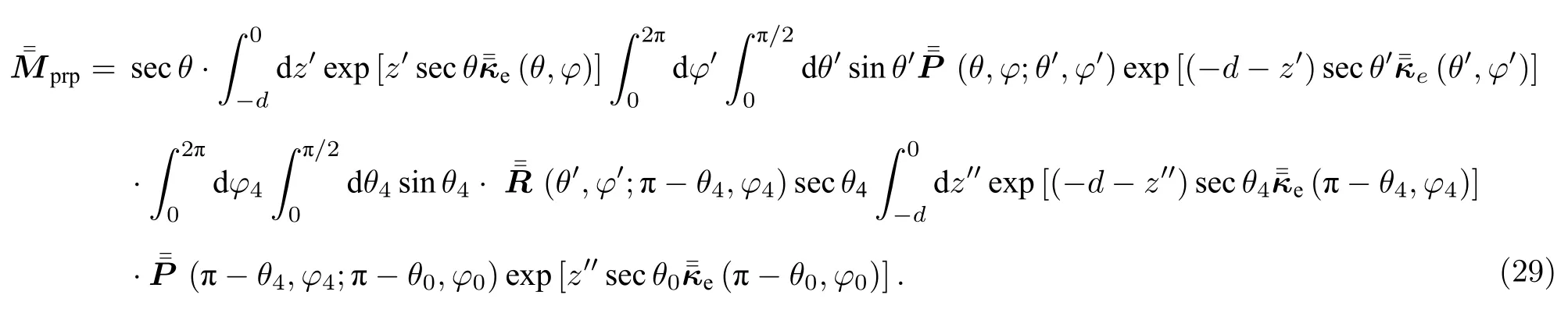
(26)—(30)式中的散射角在图(3)中标出并说明,角度积分(包括θ和π),本文在程序计算的过程都采用高斯积分处理和计算,根据角度积分的范围可选择不同的积分点个数,一般对角度2π 积分可选取最多20 个高斯积分点.

4 数值仿真和分析

4.1 粒子形状对后向散射系数的影响

算例1首先,考虑一个下垫面上粒子层模型,粒子层高度为300 cm.分别考虑当粒子层中均匀分布3 种不同形态的粒子的情况:

1)GRG 近似椭球粒子,粒子半径为0.1 cm,半高为5 cm,粒子介电常数为(14.1,4.5),随机取向欧拉角为β∈(0°,30°),γ∈(0°,360°)取平均,粒子在粒子层中的占空比为0.003;

2)竖直圆柱粒子,圆柱半径为1 cm,半高为50 cm,粒子介电常数为(19.6,8.1),粒子在粒子层中占空比为0.003;

3)倾斜圆柱粒子,圆柱尺寸与2)相同,固定取向欧拉角为β,γ=10..

其中,下垫面采用IEM 半解析粗糙面建模方法,粗糙面的均方根高度σ为0.2 cm,相关长度l为5 cm,粗糙面介电常数εr为(14.1,5.0).

分别仿真粒子层在C 波段(频率为5.3 GHz)下,粒子层后向散射系数〈σvv〉,〈σhh〉,〈σvh〉,〈σhv〉随入射角θi的变化规律曲线,不同形态粒子(GRG近似椭球,圆柱粒子)的散射矩阵表达式,以及相矩阵形式引用参考文献[6-9].

图4(a)和图4(d)是粒子为均匀取向、均匀分布的GRG 椭球粒子时,粒子层的同极化、交叉极化的后向散射系数随入射角度变化的曲线.图4(b)和图4(e)是粒子为均匀分布的竖直圆柱粒子时,粒子层的同极化、交叉极化的后向散射系数随入射角度变化的曲线.图4(c)和图4(f)是粒子为均匀分布的倾斜圆柱粒子时,粒子层的同极化、交叉极化的后向散射系数随入射角度变化的曲线.

图4 不同形态粒子的粒子层后向散射系数对比 (a)取向角均匀椭球粒子层同极化后向散射系数;(b)竖直圆柱粒子层的同极化后向散射系数;(c)固定倾斜角圆柱粒子层的同极化后向散射系数;(d)取向角均匀椭球粒子层的交叉极化后向散射系数;(e)竖直圆柱粒子层的交叉极化后向散射系数;(f)固定倾斜角粒子层的交叉极化后向散射系数.Fig.4.Backscattering coefficients of particle layers with different morphology particles:(a)Co-polarization backscattering coefficient of a layer of ellipsoid particles with uniform orientation angles;(b)the co-polarization backscattering coefficient of a layer of vertical cylindrical particles;(c)the co-polarization backscattering coefficient of a layer of cylindrical particles with fixed inclination angles;(d)the cross-polarization backscattering coefficient of a layer of ellipsoid particles with uniform orientation angles;(e)the cross-polarization backscattering coefficient of the vertical cylindrical particle layer;(f)the cross-polarization backscattering coefficient of the particle layer with a fixed inclination angle.

从数值结果可以看出,当粒子层中均匀分布取向角均匀的GRG 椭球粒子时,VRT 方程的二阶解和一阶解量级和趋势一致,整体区别较小,在交叉极化下二阶解的散射系数略大于一阶解,这是由于对于分布和取向都均匀的椭球粒子层,电磁进入粒子层后,在各个方向的散射强度都基本一致,无较强散射,粒子间的二次散射以及粒子-粗糙面的三次散射的作用都较小,因此,二阶解的散射系数与一阶解的数值基本一致.

当粒子层分布圆柱粒子时,由于圆柱粒子随入射角改变有一定规律变化,例如竖直圆柱粒子随入射角增大呈波动性上升趋势,所以当入射角较大时,圆柱粒子间产生强散射互作用,在各个方向的散射增强,圆柱粒子二次散射的强度和概率增大,粒子层存在较强的多次散射,影响粒子层整体的后向散射系数,VRT 二阶解的数值和一阶解区别较大,交叉极化及其曲线趋势变化明显.当圆柱粒子的取向角发生改变,产生强散射的角度发生变化,二阶解的多次散射互作用减小.

图4(b),(c),(e)和(f)中产生“多峰现象”,单个竖直圆柱粒子的散射特性随入射角度变化有明显的波动起伏,会出现若干个波峰波谷;对于本文出现的现象,分析将圆柱看作直线目标(特别是该参数的细长圆柱),直线目标的散射强度可以看作若干个散射中心点的共同作用[1,2],不同入射角电磁波入射圆柱散射后,圆柱上散射强度会在角度改变的过程中发生相位叠加或者相位消减,因此圆柱的散射特性曲线是随入射角度增大而“波动形增长”

VRT 仿真中圆柱粒子的散射相矩阵(衰减置零)和VRT 粒子一次散射项有一致性,考虑到对粒子不同位置的积分(Z方向)以及消光衰减的作用,VRT 圆柱粒子散射层会出现“多峰现象”.在VRT 二阶解中,不仅需要考虑粒子在高度上不同位置、粒子与粒子间相对距离,还有电磁波从一次散射到二次散射中漫散射的过程(文中用对散射角做积分处理),因此VRT 粒子二次散射“波动起伏”会依旧存在,但整体趋势较粒子一次散射较为平缓.同时,VRT 一阶存在粒子与粗糙面的二次散射相干作用,二阶解存在粒子与粗糙面间三次散射作用,粗糙面的单次散射作用是随入射角逐渐减小的,一般减小得快慢与粗糙面、谱分布有关,而圆柱粒子的散射系数总体是随入射角增大的,粒子与粗糙面的互作用也是波峰产生的原因,这些因素都是本文算例波峰波谷产生的原因.

算例2仿真含有混合粒子的粒子层后向散射系数随入射角后向散射系数,混合粒子的参数为算例1)中的椭球粒子和算例2)中的圆柱粒子按照其各自占空比混合计算,占空比混合模型计算公式为

图5 混合粒子的同极化散射系数对比Fig.5.Comparison of co-polarization scattering coefficients of mixed particles.

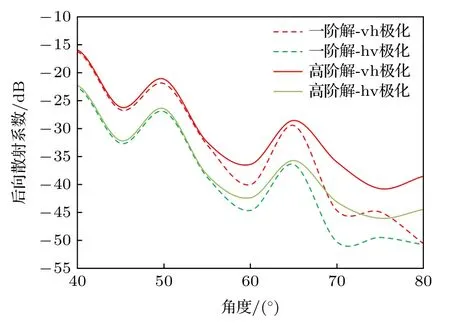
图6 混合粒子的交叉极化散射系数对比Fig.6.Comparison of cross-polarization scattering coefficients of composite particles.

从结果可以看出,混合粒子层中存在两种形态不同的粒子,取向均匀的针状椭球和竖直圆柱,两种粒子的占空比一致.由之前的结果可知,椭球粒子随入射角度增大散射系数减小,VRT 二阶解的作用较小,散射系数随角度变化趋势基本和一阶解的基本一致.

入射角增大后,圆柱粒子的散射系数逐渐增大,粒子间互作用增大,粒子层多次散射增强,VRT 二阶解对粒子层的散射作用明显.当入射角逐渐增大后,圆柱粒子的散射系数大于椭球粒子,因此在混合粒子-粒子层模型中,根据(24)式可知圆柱粒子的散射系数对粒子层整体的影响明显,VRT 二阶解对混合粒子粒子层的作用增大.在混合粒子层中,在低掠角入射范围内,VRT 二阶解的多次散射作用较大,影响后向散射系数的数值结果.可进一步研究更多种混合粒子的后向散射系数的变化规律.

4.2 粒子占空比对后向散射系数的影响

算例3为了验证VRT 方程二阶迭代散射解的正确性,以及其对VRT 数值求解后向散射系数的作用,固定粒子模型为竖直圆柱,倾斜欧拉角均固定为10°,圆柱半径为1 cm,半长为50 cm,介电常数为(19.6,8.1),粒子层厚为300 cm,固定入射角θi=50°,仿真下垫面上一层圆柱粒子的后向散射系数〈σvv〉,〈σhh〉,〈σvh〉,〈σhv〉随粒子密度(占空比)的变化曲线,仿真结果如图7 和图8 所示.

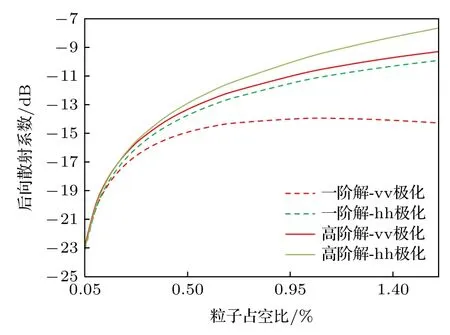
图7 不同占空比下粒子层的同极化散射系数对比Fig.7.Comparison of the co-polarization scattering coefficients of particle layers with different duty cycles.

图8 不同占空比下粒子层的交叉极化散射系数对比Fig.8.Comparison of cross-polarization scattering coefficients of particle layers with different duty cycles.

结果表明:随着粒子层粒子密度(粒子占空比)的不断增减,VRT 方程的一阶解和二阶解的后向散射系数都在不断增大,但是无论是同极化还是交叉极化,VRT 二阶的后向散射系数的增加幅度和趋势明显大于VRT 一阶解.二阶解同极化、交叉极化的散射系数都不同于一阶解散射系数变化相对平缓,由于随着粒子层粒子数量不断增加,粒子间二次散射作用的概率不断增大,使得粒子层的总散射作用逐渐增强.同时,粒子和粗糙面间的多次散射也是交叉极化散射系数逐渐增大的重要原因.在高密度粒子的粒子层中,二阶解的多次散射对整体环境后向散射系数起到较大增强作用..

4.3 草地沙盘实测与VRT 模型的对比

算例4测量一个半径0.7 m,厚0.1 m 草地沙盘的散射系数,用该草盘模型的物理参数建立一个VRT 模型,如图9 和图10 所示.该VRT 模型的参数如下:粒子层厚10 cm,GRG 近似椭球粒子尺寸为h=5 cm,r=0.1 cm,粒子介电常数为(14.98,1.466)且占空比为0.05,欧拉角取向为,β,γ∈(0,10°).粗糙面模型为IEM,其介电常数为(26.7,11.7),粗糙度σ=0.3 cm,l=1.0 cm,电磁波频率为10 GHz.

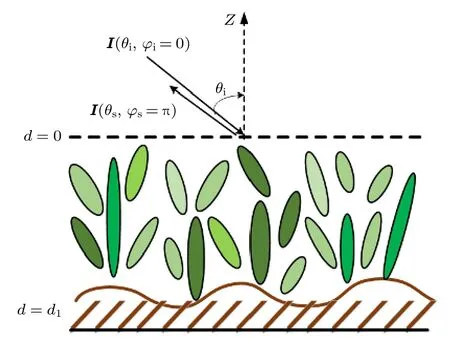
图9 VRT 模型示意图Fig.9.Grass of VRT model.

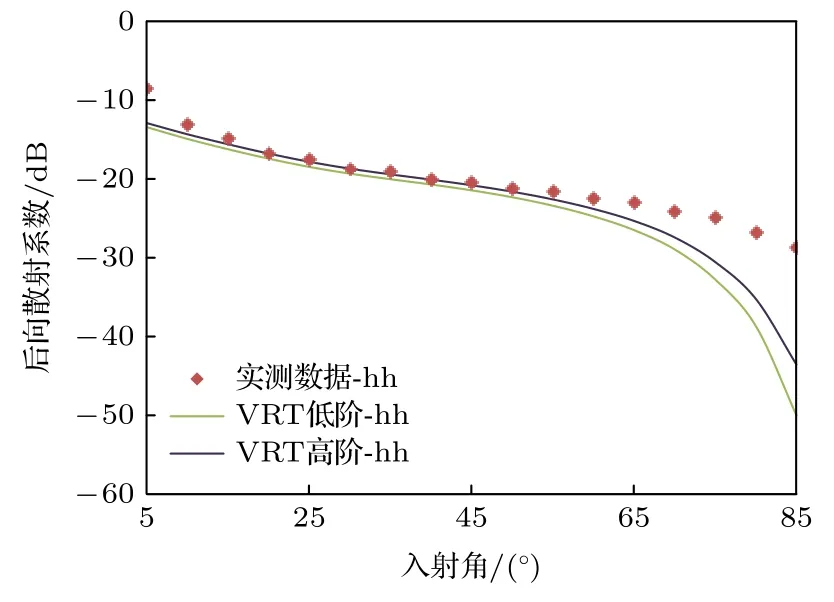
图10 仿真结果和实测数据对比图Fig.10.Comparison diagram of simulation results and measured data.

分别计算该模型的VRT 低阶解和VRT 二阶解的后向散射系数,并与该草盘的实测数据进行对比.

图10 仿真结果表明,VRT 建模仿真草地能较好地拟合所测得的实测数据,VRT 高阶解仿真结果曲线与实测结果基本吻合且无明显波动,呈现单调递减,且GRG 近似椭球取向角范围较大,仿真粒子的随机性能更好模拟实测沙盘草地的特性.

5 总结

本文将下垫面上方粒子层在Z轴方向上分成若干层,推导出了含有下垫面的VRT 方程的二阶散射解.分析不同形态的粒子对散射系数的影响,比较了非球型粒子的一阶、二阶散射迭代解的差异.数值结果表明:取向均匀的粒子形态,粒子间多次散射作用较弱,从而对粒子层散射系数的影响较小.对于在特定角度下存在较强散射作用的粒子形态,粒子间多次散射作用较大,从而对粒子层散射系数的影响较大.随着粒子数量增多,粒子层散射强度因多次散射作用影响较大,VRT 二阶解对数值结果有较大帮助.该方法可以更好地描述粒子间、粒子与粗糙面之间的相干作用.