利用重归一化Numerov 方法研究超冷双原子碰撞

白净 谢廷

1)(大连职业技术学院电气电子工程学院,大连 116035)

2)(中国科学院大连化学物理研究所,分子反应动力学国家重点实验室,大连 116023)

采用重归一化Numerov 算法求解关于超低温双原子碰撞问题的非含时薛定谔方程组.以39K-133Cs 碰撞为例,研究了超低温下双原子Feshbach 共振的性质.结果表明,重归一化Numerov 算法可以很精确地描述超冷条件下碰撞过程.与改进的logarithmic derivative 算法相比,在同等参数条件下,重归一化Numerov 方法在计算效率上虽然有一定劣势,但在大格点步长参数范围内有着更好的稳定性.提出重归一化Numerov 和logarithmic derivative 算法相结合的传播方法,在保证结果精度的同时大大减少了计算时间.此项算法也可以应用于求解任意温度下的两体碰撞耦合薛定谔方程组.

1 引言

在过去几十年里超冷分子的制备和应用经历了长足发展.在研究超低温原子和分子气体相互作用的实验中,Feshbach 共振扮演着一个主要角色[1].由于在超低温下碰撞粒子对的动能极低,这使得我们可以通过磁场调节碰撞粒子不同通道之间的能量差.当粒子对在入射通道的散射态和闭通道中束缚态能量发生简并时,即为Feshbach 共振发生,表征原子间相互作用的散射长度会发散至无穷大[2].同时,入射通道的散射波函数在短程处增强,碰撞粒子对会迅速转换为弱束缚分子态[3].由于不同通道间能量差和粒子的性质有关,Feshbach 共振只发生在一些特定强度的磁场下.许多实验小组利用磁场来研究和控制超冷气体的动力学和结构性质[4].

当前有几个研究小组发展了不同的计算方法来预测磁场中Feshbach 共振的性质,主要分为以下3 种:1)量子亏损理论(quantum defect theory).通过把相互作用势的散射长度作为输入参数并忽略精确的短程相互作用势,Gao[5]发展了解析的量子亏损模型,使其可求解超冷碰撞原子对的散射性质及磁诱导Feshbach 共振.2)渐近束缚态模型(asymptotic bound state model).Tiecke 等[6]利用单三重态的弱束缚态的能量本征值作为输入参数,发展了渐近束缚态模型,使其可以预测磁诱导Feshbach共振的位置及宽度.3)密耦方法(close-coupling method).通过数值求解完整哈密顿的薛定谔方程组,可以获得精确的散射信息[7].这是一种没有使用任何近似的方法,因此也常被用来解释实验观测结果.

对于精确求解密耦方程,人们发展了几种不同的数值方法,如对数导数方法(logarithmic deriviative,LOGD)[8]、R 矩阵方法[9]、龙格-库塔法[10]、Numerov方法[11]等.其中,LOGD 被认为是最稳定也很高效的方法,常用来作为数值求解耦合薛定谔方程组的标准.Numerov 方法可以给出散射态和束缚态的具体波函数,多用于单通道问题.由于超低温下磁场耦合了不同的束缚态通道,Numerov 方法传播的波函数会发散至无穷大,并不适合用来研究共振过程[12],为此人们发展了更加稳定的重归一化Numerov方法 (renormalized Numerov,RN)[13].Colavecchia 等[14]利用改进的RN 方法研究了温度大于1 K 时的三原子分子碰撞反应散射,发现了RN 方法在研究碰撞解离时比LOGD 方法具有更好的收敛性.Karman 等[15]推导了可以使用变步长的RN 方法,比较了不同算法的精度,研究了温度为1 K 时的分子-分子散射碰撞,并给出了不同通道的散射波函数.Blandon 等[16]将映射格点方法和RN 方法相结合,改进了计算效率.然而关于RN 方法在超低温下双原子散射碰撞应用并未被详细研究.在这项工作中,使用RN 方法来研究超低温双原子碰撞过程.

对于碱金属双原子分子体系,处于绝对基态的超冷KCs 分子具有较大的永久电偶极矩,在低温下有很强的长程偶极相互作用,是许多实验组的研究热点[17,18].本文以39K-133Cs 两体碰撞为例,研究了超低温下的Feshbach 共振性质,并与LOGD 方法作比较.结果表明RN 方法可以很精确地给出散射信息,并且在大格点步长情况下有着比LOGD更好的稳定性.在此基础上,提出RN 和LOGD 相结合的传播方法,在保证精度的同时可以大大减少计算时间.此项工作为研究散射碰撞提供了额外一种可靠的数值方法.

2 计算方法

2.1 外磁场中碱金属双原子碰撞Schrödinger方程

外磁场中超低温双原子碰撞的总哈密顿可以表示为

式中,μ是双原子体系的折合质量,R是原子核间距,l是双原子体系的轨道角动量量子数,θ和φ分别表示空间极化角和方位角.(1)式右边第一项表示相对运动动能,第二项是离心势能.(1)式右边第三项是原子间的相互作用势,可表示为

式中,VS(R)表示碰撞原子对在总自旋态S的绝热相互作用,MS是S沿着磁场方向的投影量子数,这里假设磁场方向和空间量子z轴平行.

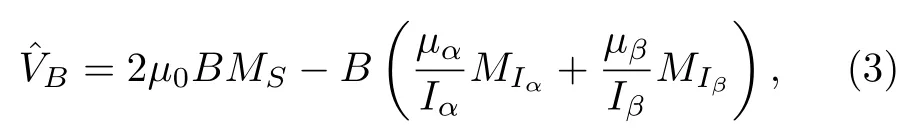
式中,μ0表示玻尔磁子,B是磁场强度,μα(β)表示原子α(β)的核磁矩,Iα(β)和分别表示原子α(β)的核自旋及其在磁场方向的投影量子数.

式中,γα(β)表示原子α(β)的超精细相互作用常数,Sα(β)是原子α(β)的电子自旋量子数.

定义完全非耦合基矢

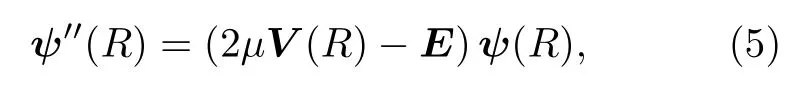
式中,ψ(R)是体系的总波函数矩阵形式,V(R)是势能相互作用矩阵,E是碰撞粒子对的总能量矩阵.求解此方程组,可以获得散射碰撞信息等参量.

2.2 多通道重归一化Numerov 方法

Numerov 方法是一种可以用于求解一维薛定谔方程的有效方法.在数值计算中,通常把原子核间距R离散为等间距的格点,然后求解不同格点位置下的波函数.对于单通道情况,其计算核心是三点迭代关系式[13]

这里ψn表示在第n个格点处的波函数;Tn=—(μh2/6)(Vn—E),其中h为格点之间的间隔,Vn表示势能在第n个格点的值,E是入射通道的碰撞能.

通过对(6)式作两次变换,可得RN 传播算法.具体如下:在第一步变换中定义Fn=(1—Tn)ψn,并代入(6)式中,可得

式中Un=(2+10Tn)/(1—Tn).第二步变换是将三点迭代关系替换为两点迭代.首先定义比率Qn=Fn+1/Fn,将其代入(7)式中,则得两点迭代关系式

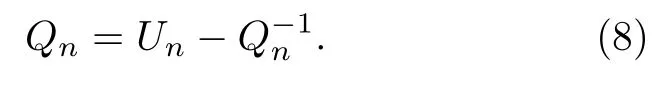
进一步地,可得波函数在第n个格点处的导数

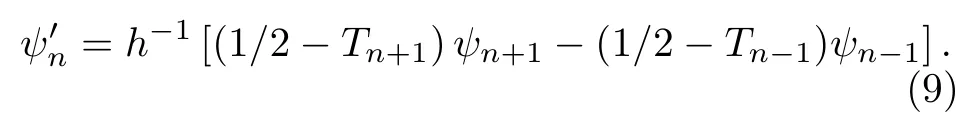
式中An=1/2(1—2Tn)/(1—Tn).由于Qn定义的是前后相邻格点的波函数比例,因此被称作重归一化方法.注意上面给出的单通道LOGD 参数是在RN方法中的迭代关系式,不同于文中所说的LOGD 方法.对于超低温双原子散射碰撞,通常入射通道和其他多个通道耦合在一起,(10)式应记为矩阵形式.为了完整性,写出多通道LOGD 参数的矩阵形式

式中,I为单位方阵,An=1/2(I— 2Tn)(I—Tn)—1.在数值计算中,一般设置初始格点Qn=1=1020×I,将(10)式由短程向长程传播,可以得到y矩阵在第n个格点的值.当原子核间距Rn足够大时,碰撞原子对的波函数可表示为[19]

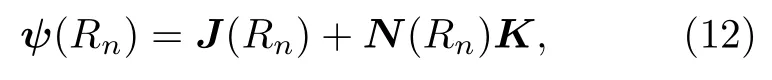
式中,K是和Rn无关的反应矩阵,J和N都是对角矩阵.对于开通道情况,J和N的矩阵元可表示为Riccati-Bessel 函数[20]

对于闭通道情况,其矩阵元可以表示为修正的第一和第二类球Bessel 函数[20]

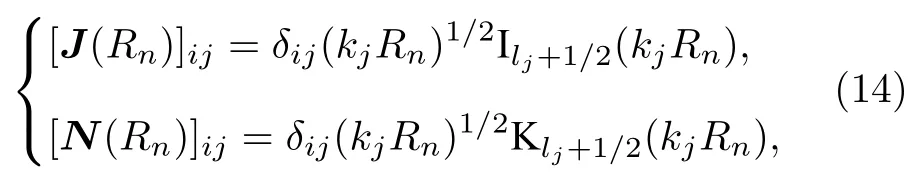
式中kj和lj分别表示第j个通道的波矢和分波量子数.对(12)式求一阶导再除以(12)式,可得K矩阵的表达式

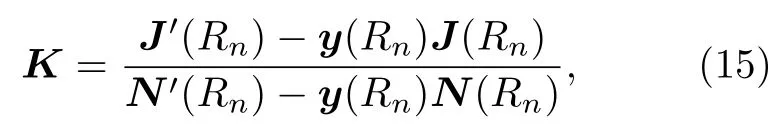
从而得到S矩阵[21]

式中i 表示虚数单位.

在获得S矩阵后,就可以得到散射长度等信息.对于s 波通道来说,其散射长度a可用下式来计算[22]

式中,δ(k)表示第j个通道的相移,Sjj(k)是S矩阵中第j个通道的对角矩阵元.

3 结果与讨论

本部分研究了39K-133Cs 超低温两体碰撞.由于碰撞能极低,高阶分波对散射的贡献很小,可以只考虑最低的入射s 波通道.虽然偶极-偶极相互作用可以耦合s 和d 波,d 波可能诱导新s 波共振[23],但是本文关注的是数值方法的准确性和计算效率,因此,在计算中偶极相互作用被忽略.

采用Ferber 等[24]在2013 年由光谱数据拟合的基单重态和三重态的势能面数据.图1 展示了39K-133Cs 双原子体系的基态势能相互作用.在这个体系中能量最低的电子态解离极限是39K(4s)+133Cs(6s),相关的电子态为基单重态X1Σ+和a3Σ+,对应的散射长度分别是—18.37a0和82.24a0,a0是玻尔半径.在求解耦合微分方程组时选定短程起点为R=3a0,长程终点为R=2000a0,每个格点间的间隔固定为0.002a0,碰撞能为1 nK.在这样的低能区域,s 波散射性质和碰撞能无关.

图1 39K-133Cs 体系基单重态和三重态相互作用势Fig.1.Ground electronic potential curves of singlet and triplet states in 39K-133Cs.

由于39K 和133Cs 原子最外层各有1 个电子,所以它们的电子自旋量子数都是1/2,核自旋量子数分别为3/2 和5/2,在磁场中能量最低的超精细态通道为|fK=1,mfK=1〉+|fCs=3,mfCs=3〉,这里f和mf分别表示单个原子的总自旋量子数及其在磁场方向的投影.在磁场中,碰撞粒子对的总自旋投影量子数Mf=mfK+mfCs守恒.当入射通道为s 波|fK=1,mfK=1〉+|fCs=3,mfCs=3〉时,它是唯一开通道,并和另外7 个Mf=4 的闭通道通过塞曼超精细相互作用耦合在一起.图2 为入射通道为|fK=1,mfK=1〉+|fCs=3,mfCs=3〉时的s 波散射长度,可以看到散射长度在某些磁场位置展示了发散的特性,这表明发生了共振.因为改变磁场强度同时也改变了开通道和闭通道间的能量差,从而使得闭通道的束缚态可以和开通道散射态发生简并.图中展示的5 个理论共振位置也被其他研究小组预测到[22],而实验上人们只发现了位于341.9 G (1 G=10—4T)和421.6 G 处的共振信号[25],另外3 个共振并没有被观测到.需要指出的是,正无穷大的散射长度表明原子间相互作用是强排斥的,反之是强吸引的.在实验上需要制备某些种类的超冷分子时,人们总是调节磁场由强吸引区域到强排斥区域,这样才会得到弱束缚的超冷分子,然后通过受激拉曼绝热通道技术转移至绝对基态就可以获得绝对基态的超冷分子[1].在单个共振附近,散射长度a可以表示为[26]

图2 在入射通道计算的磁场0—1000 G 范围内的s 波散射长度,红线标记录5 个共振位置Fig.2.Calculated s-wave scattering length in the incoming channel with field range 0 —1000 G.The five resonant positions are labeled with red lines.

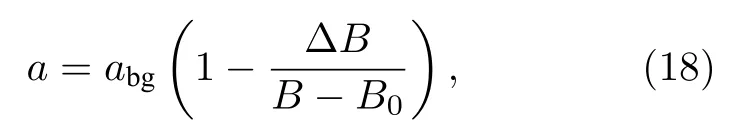
式中,abg是背景散射长度;ΔB是共振宽度,定义为散射长度为0 和无穷大时磁场强度之差;B0是共振位置,即散射长度为无穷大的磁场值.(18)式中比较重要的参数是共振宽度,它是衡量共振强度的参量.由于实验装置中磁场强度具有一定的不确定度,因此宽共振在实验上容易被发现,也更有应用价值[27].根据(18)式,对计算的散射长度在所有共振附近进行了拟合,并把参数列于表1 中.作为对比,利用Manolopoulos[28]发展的改进的定步长LOGD 方法得到的结果也被列入表中.

从表1 可以看到,由两种方法得到的共振参数几乎一致,这表明了RN 方法的计算精度很高,可以和LOGD 方法相比拟.此外,也可以看到大部分s 波共振普遍偏窄(＜1 G),这是由于39K-133Cs体系的单三重态的散射长度差异较小(—18.37a0和82.24a0),不同通道之间的耦合较弱导致的.

表1 两种计算方法得到的共振位置、共振宽度和背景散射长度参量Table 1. Calculated resonant positions,widths and background scattering lengths in the incoming channelby both methods.

表1 两种计算方法得到的共振位置、共振宽度和背景散射长度参量Table 1. Calculated resonant positions,widths and background scattering lengths in the incoming channelby both methods.

接下来比较了两种方法的计算效率.图3(a)给出了利用两种方法计算散射长度的程序运行时间随格点数的变化.由于单一磁场强度下两种方法计算散射长度的时间均很短,存在较大误差,为了比较的准确性,这里列出了计算100 个磁场强度下散射长度的总时间.计算中所有的参数都选取一致,并且都使用了固定步长方法.格点数变化范围为2×105到2×106,对应的格点步长范围为10—2a0至10—3a0.可以看到LOGD 方法在计算效率上有一定优势,然而在少格点数情况下差异缩小,这主要是由于在RN 方法中(8)式中的Un是精确计算得来的,而改进的LOGD 方法使用了参考势的解析解代替精确解[28],在对格点循环过程中少了一步矩阵相乘运算.如果采用和LOGD方法的近似处理方法,原则上这两者的计算时间应该很接近,这也是当前RN 方法可以继续优化的一方面.图3(b)给出了磁场为1 G 时随总格点数变化的散射长度.可以看到LOGD 方法在少格点数情况下计算误差增大,而RN 方法在少格点数(大格点步长)情况下表现的更稳定.这个现象在任意磁场强度下都可以被观测到,表明使用RN 方法时可以采用较少的格点数来减少计算时间.

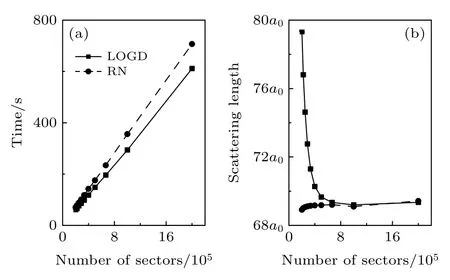
图3 (a)采用两种方法计算100 个磁场强度下散射长度的计算时间随格点数的变化;(b)在磁场为1 G 时散射长度随格点数的变化Fig.3.(a)Computational time of scattering length at 100 magnetic fields as a function of number of sectors by using two methods;(b)the scattering lengths as a function of number of sectors at 1 G.

第2 节介绍了RN 的计算基础是泰勒展开,高阶展开项被忽略(h＞6),也被称为“解跟随”方法,适合用于势能变化比较剧烈的短程区域.而改进的LOGD 方法使用了近似的参考势,是一种“势能跟随”方法,适合势能变化比较平缓的长程区域.根据上面的计算结果提出一种新传播方法:在双原子核间距短程处使用RN 方法,在长程处使用变步长LOGD 方法.这种方法可以利用两者各自的优点,从而最大程度地减少计算时间.表2 列出使用上述新传播方法得到的5 个共振位置总误差.这里设定短程和长程接合点为R=20a0,即R＜20a0范围使用RN 算法,R＞20a0范围使用LOGD 算法,注意更大的接合点会降低计算效率,而更小的接合点会引起较大的计算误差.可以看到当RN 方法在短程传播步长小于 0.008a0时,5 个共振位置的总误差小于1 G,仍可以得到较为精确的共振位置.和图3(a)相比计算总步数大大减少,计算效率很高.预期此传播方法应用在复杂体系可以减少计算时间,扩大研究体系范围.

表2 采用短程RN 和长程变步长LOGD 相结合的传播方法得到的共振位置总误差,这里两种方法的接合点在R=20a0.第一列ΔR 表示在RN 方法中使用的固定格点步长,第二列NRN 表示RN 方法在短程传播的总步数,第三列NLOGD 表示在变步长LOGD 方法在长程传播的总步数,第四列表示使用两者结合方法产生的所有共振位置误差的绝对值总和Table 2. Total errors of resonant positions by using the method combining RN method in short range with LOGD with variable step size in long range,where the connected point is located at 20a0.The first column,ΔR,represents the fixed step size in RN method.The second and third columns,NRN and NLOGD,denote the steps propagated in RN and LOGD methods,respectively.The last column is the sum of errors for all resonant positions.

表2 采用短程RN 和长程变步长LOGD 相结合的传播方法得到的共振位置总误差,这里两种方法的接合点在R=20a0.第一列ΔR 表示在RN 方法中使用的固定格点步长,第二列NRN 表示RN 方法在短程传播的总步数,第三列NLOGD 表示在变步长LOGD 方法在长程传播的总步数,第四列表示使用两者结合方法产生的所有共振位置误差的绝对值总和Table 2. Total errors of resonant positions by using the method combining RN method in short range with LOGD with variable step size in long range,where the connected point is located at 20a0.The first column,ΔR,represents the fixed step size in RN method.The second and third columns,NRN and NLOGD,denote the steps propagated in RN and LOGD methods,respectively.The last column is the sum of errors for all resonant positions.

4 结论

本文利用RN 和LOGD 数值方法计算了K-Cs体系超低温下的散射性质.结果表明RN 方法可以用于精确求解超低温下的两体散射过程,并且在少格点数情况下的稳定性允许人们使用更大的格点步长,从而减少计算时间.另外,提出了短程固定步长RN 和长程变步长LOGD 相结合的传播方法以提高计算效率.此方法对于求解任意温度下的两体碰撞问题同样有效.