有限元强度折减法的边坡稳定性及参数敏感性分析

王龙

（陕西省西咸新区沣西新城管理委员会 陕西 西安 712000）

1 有限元强度折减法基本原理及屈服准则与破坏准则的选用

1.1 强度折减法原理

强度折减法被许多学者广泛应用，他们提出了一个抗剪强度折减系数的概念［1］。在极限状况下，外荷载所产生的实际剪应力与抵御外荷载所发挥的最低抗剪强度即按照实际强度指标折减后所确定的、实际中得以发挥的抗剪强度相等［2］。当假定边坡内所有土体抗剪强度的发挥程度相同时，这种抗剪强度折减系数相当于传统意义上的边坡整体稳定安全系数FS，又称为强度储备安全系数，这与极限平衡法中所给出的稳定安全系数在概念上是一致的［3］。

1.2 屈服准则的选用

安全系数的大小与所采用的屈服准则密切相关，选取不同的屈服准则，可以得出不同的安全系数［4］。本文与传统的极限平衡法一样，采用摩尔库伦屈服准则［5］。

1.3 破坏准则的选用

利用ABAQUS软件，在有限元计算分析中，选取不同的强度折减系数Fr，并对折减后的强度参数进行分析，观察有限元计算是否收敛。在计算过程中不断地增加Fr，当达到临界破坏点时的强度折减系数Fr就是边坡的稳定安全系数FS。本文以边坡坡面是否形成连续的贯通区和位移曲线拐点作为评价边坡稳定性的标准［6］。

2 某边坡稳定性分析

2.1 不同工况边坡稳定性分析

本文基于某水电站边坡最危险剖面进行边坡稳定性强度折减法分析。该边坡为非均质土坡，坡高146m，模型尺寸为底边长372m，高192m，顶端长138m。坡体上部为松散体（崩坡积和冲洪积），下部为玄武岩和千枚岩。地下水位线均采用资料中给出的水位线，松散土体选取相应的参数。

边坡稳定性有限元计算所受荷载为自重，边界条件为底端全约束，两侧法向约束。对土体材料强度c和φ值进行折减。

2.1.1 天然状况（水库蓄水前）边坡稳定性

通过计算，得出该边坡塑性图（见图1）、边坡顶点处安全系数随位移变化的拐点图（见图2）及边坡水平、竖直方向位移等值线云图（见图3、图4）。

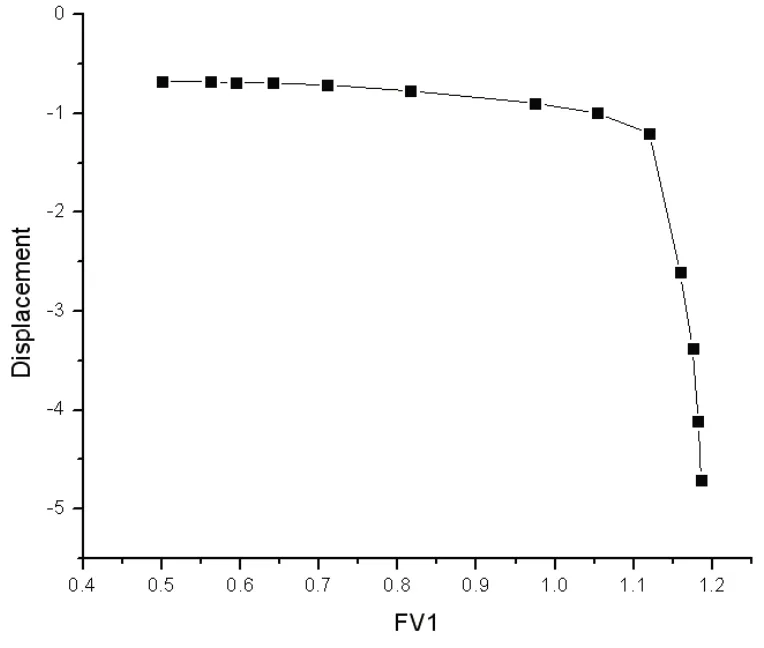
图2 FV1随U1的变化关系

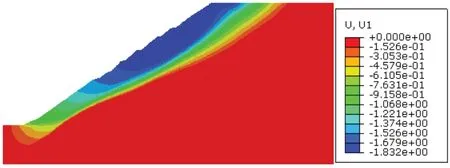
图3 水平方向位移等值线云图

图4 竖直方向位移等值线云图

以特征部位（坡顶点）的位移拐点曲线和是否形成了连续的塑性贯通区这两个评价标准来提取该边坡的安全系数。根据塑性图，得出边坡安全系数为1.144；由位移变化的拐点图，可以得出边坡安全系数为1.140。可以看出，以此两种评价标准判断边坡稳定安全系数十分接近，可以用此方法来评判边坡稳定性。

2.1.2 其他工况下边坡稳定性分析

通过计算，得出天然状况（水库蓄水前）+遭遇暴雨、天然状况（水库蓄水前）+遭遇地震、正常蓄水位和校核洪水位+遭遇暴雨工况下边坡稳定性分析，得出边坡该边坡安全系数如表1所示。

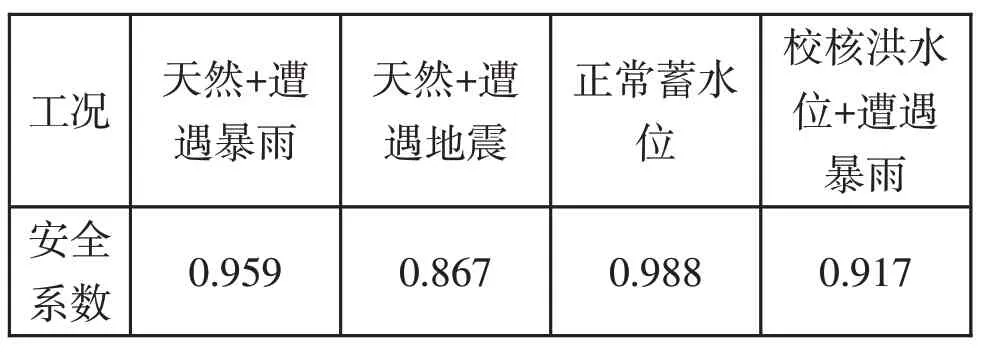
表1 不同工况下边坡安全系数表

通过各种工况计算，得出此边坡只有在天然状况下处于安全状态，在其他工况下均处于不稳定状态，需要进行一定的边坡加固措施，如压坡、削坡或者锚杆支护等。

2.2 边坡各项参数敏感性分析

对此边坡进行敏感性分析，具体处理方法为：若对材料强度c进行敏感性分析，则需要固定材料的其他参数φ、E、μ、λ，让c在一定范围内进行变化，得出不同的安全系数，整理如下。

2.2.1 强度参数敏感性分析

首先，对粘聚力c进行敏感性分析，固定其余4 个参数不变，粘聚力的值分别为30kPa、50kPa、70kPa 和90kPa时，计算边坡的安全系数，如表2所示，得出曲线如图5所示。其次，对内摩擦角φ进行敏感性分析，固定其余4 个参数值保持不变，内摩擦角的变化值分别为28°、30°、33°和38°时，计算边坡的安全系数，如表2所示，得出曲线变化如图6所示。

表2 安全系数随粘聚力和内摩擦角的变化表

图5 安全系数随粘聚力的变化曲线

2.2.2 刚度参数敏感性分析

首先，对弹性模量E进行敏感性分析，固定其余4个参数不变，弹性模量的值分别为21MPa、26MPa、30MPa 和35MPa 时，计算边坡的安全系数，如表3 所示，得出曲线如图7所示。其次，对泊松比μ进行敏感性分析，固定其余4个参数值保持不变，泊松比的变化值分别为0.25、0.28、0.30和0.33时，计算边坡的安全系数，如表3所示，得出曲线变化如图8所示。

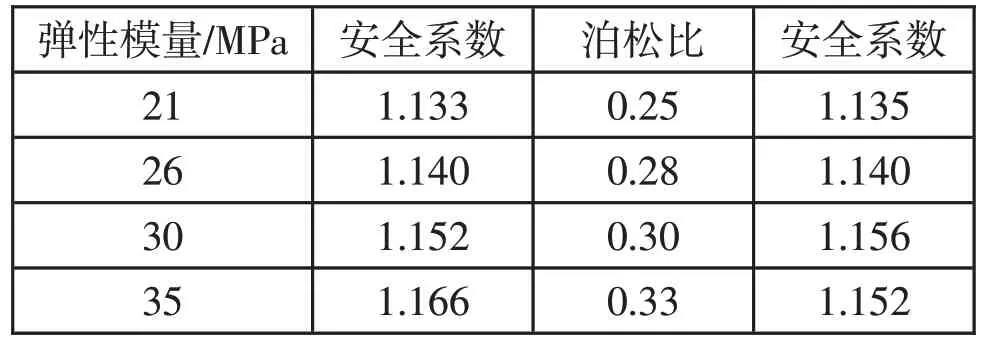
表3 安全系数随弹性模量和泊松比的变化表

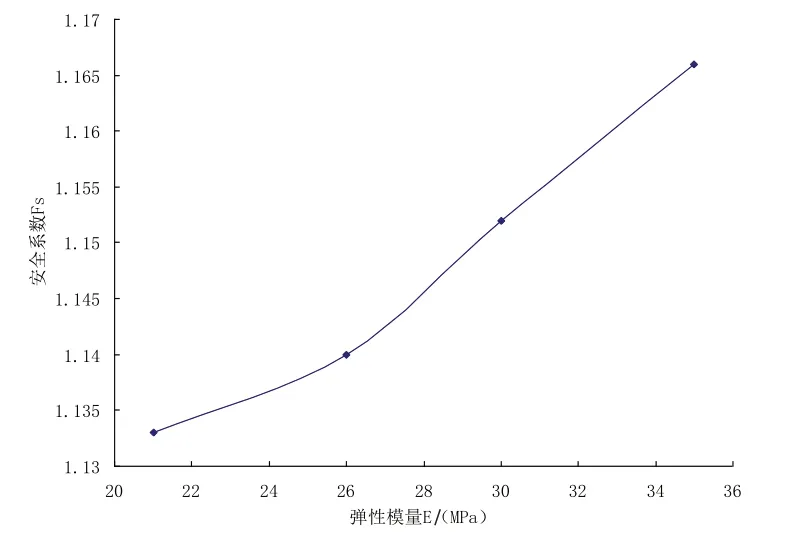
图7 安全系数随弹性模量的变化曲线

图8 安全系数随泊松比的变化曲线

2.2.3 其他参数敏感性分析

对容重λ 进行敏感性分析，固定其余4 个参数不变，容重的值分别为17.5kN/m2、19.5kN/m2、21.5kN/m2和23.5kN/m2时，计算边坡的安全系数，如表4所示，得出曲线图如图9所示。

表4 安全系数随容量的变化表

图9 安全系数随容量的变化曲线

3 结论

（1）有限元强度折减法不需要对滑动面形状和位置做假定，通过强度折减使边坡达到不稳定状态时，非线性有限元静力计算将不收敛，此时的折减系数就是边坡稳定安全系数，同时可以得到边坡破坏时的滑动面和位移、应力情况。

（2）本文利用有限元强度折减法，对参数进行敏感性分析，得出如下结论。

材料强度参数：边坡稳定安全系数随着粘聚力c和内摩擦角φ的增大而增大，且基本呈线性变化；内摩擦角对边坡稳定安全系数的影响大于粘聚力对其的影响。

材料刚度参数：边坡稳定性安全系数随着弹性模量的增大而增大，且基本呈线性变化；随着泊松比的增大，安全系数先增大后减小，说明泊松比对安全系数的影响存在一个最优值。

材料其他参数的影响：边坡稳定性安全系数随着容重λ的增大而减小，也基本呈线性变化。

（3）本文采用非线性有限元强度折减系数法，由程序自动求得边坡的危险滑动面及相应的稳定安全系数。通过算例，分析了此法的可行性，为实际工程做出了指导。