基于建筑聚类的“集中-分散”组合式太阳能供暖系统设计优化研究

冯平安，胡德泽，穆 婷，张思远

(1.陕煤电力集团有限公司，西安 710065；2.西安建筑科技大学，西安 710055；3.中国电建集团西北勘测设计研究院有限公司，西安 710065)

0 前 言

中国农村地区建筑布局分散，集中供暖难以普及，农村居民供暖问题始终未能得到有效解决。另一方面，农村地区拥有丰富的太阳能资源，地广人稀的分布特性使得农村太阳能资源利用条件[1]更加优越。对于布局分散的农村地区，使用集中式太阳能系统对多个用户供暖，会因热量的长距离传输损耗导致系统经济性下降，而使用完全分散的单户式太阳能供暖系统，又会因未能充分利用不同建筑热负荷之间的互补特性而降低系统整体能效。因此，简单的集中式与分散式太阳能供暖系统都难以满足建筑布局分散的农村地区供暖需求，适宜的太阳能供暖系统设计优化方法亟待提出。

空间聚类是将空间数据集中的对象分成由相似对象组成类的分析方法。若能对供暖区域首先从建筑间距与负荷互补特性的角度进行建筑空间聚类分析，再针对不同建筑集群设计各自独立的太阳能供暖系统，则能通过“集中-分散”的组合式供暖兼顾系统经济性与能效，进而解决分散区域太阳能供暖系统的优化设计问题。空间聚类方法主要包括划分聚类算法、层次聚类算法、基于密度的方法、基于网格的方法和基于模型的聚类方法等[2]，其中，基于密度的方法[3-4]可以在含有噪声的数据集中识别任意数量和形状的簇，适用于不同区域建筑群的空间聚类。相关研究中，Qiliang Liu等人[5]应用了一种新的基于密度的空间聚类算法，该方法能够在空间对象存在噪声点时检测任意形状和非均匀密度的簇。Lian Duan等人[6]提出了一种在空间数据库中发现不同局部密度簇的密度聚类算法，该方法能够解决具有不同局部密度的数据聚类问题。在将建筑群聚类与能源系统设计优化相结合的研究中，Wei Wang[7]采用了一种基于密度的聚类方法，该方法考虑空间尺寸和不同需求曲线的互补效应，提高了大型城市能源-水关联系统的优化效率和准确性。Julien F.Marquant[8]根据密度聚类算法，将城市规模的案例分为多个区域以解决多尺度能源网络规划问题。但是，以上研究多针对的是产能相对稳定的大型城市能源系统，对于波动性强的太阳能供暖系统少有涉及。

综上所述，现有将建筑群聚类与能源系统优化相结合的研究中，缺少将空间聚类方法应用于太阳能供暖系统的研究。为深入分析不同的建筑集群划分对太阳能供暖系统的设计与运行结果所造成的影响，本文在建筑群聚类的基础上，对各建筑集群的太阳能供暖系统分别进行设计优化，并通过比较多个聚类方案下的系统全生命周期成本得到最佳的“集中-分散”组合式太阳能供暖系统形式，为分散区域太阳能供暖系统设计提供理论支撑。

1 方 法

本文提出的组合优化方法流程见图1，其过程主要分为以下4个阶段：

图1 方法路线

(1)基于密度的建筑群聚类；

(2)各建筑集群中热力管网的生成；

(3)各建筑集群中的太阳能供暖系统设计优化；

(4)最优建筑群聚类方案及最优系统设计比选。

1.1 基于密度的建筑群聚类

基于密度的建筑群聚类方法中，DBSCAN算法因无需事先规定建筑集群数量、可发现任意形状建筑集群、能够识别噪声点、对离群点有较好鲁棒性等特点而最为常用。由于DBSCAN算法对初始参数设置比较敏感，本文在一定范围内调节参数邻域半径Eps与最小样本数Minpts，以得到多种聚类方案。

DBSCAN 算法执行步骤具体描述如下所示：

输入：数据集D，邻域半径Eps以及最小样本数Minpts

步骤 1：从数据集D中随机抽取一个未被处理的对象p，且在它的邻域半径Eps内满足最小样本数要求的称为核心对象；

步骤 2：遍历整个数据集，找到所有从对象p的密度可达对象(在对象集合 中，若存在一个点链p1、p2、…、pn，对于pi∈D(1≤i≤n)，且pi+1是从pi的直接密度可达，则点pn从点p1密度可达)，形成一个新的簇；

步骤 3：通过密度相连(若存在对象o，使得对象p和对象q都从o密度可达，则对象p和对象q密度相连)产生最终簇结果；

步骤 4：重复执行步骤2和步骤3，直到数据集中所有对象都为“已处理”。

通过以上步骤可知，基于密度的聚类是一组“密度相连”的对象，以实现最大化的“密度可达”。在通过DBSCAN算法对建筑群进行聚类以后，分析每一建筑集群样本点的分布，可将每一建筑集群的核心对象点确定为该建筑集群内的集中式太阳能供暖系统所在位置。

1.2 各建筑集群中热力管网的生成

通过DBSCAN密度聚类方法对建筑群进行划分后，需要确定各建筑集群内距离最短的热力管网。在对建筑群地理坐标进行预处理时，常规的Delaunay三角剖分方法可以生成各簇内建筑群的二维规划图，减少距离较远的建筑之间的管道连接，但不能生成最短的热力管网。本文在三角剖分的规划基础上，进一步应用Kruskal最小生成树算法来生成具有最小总长度的热力管网，已确保所有建筑物都已连接。

最小生成树算法假设在给定的无向图G=(V,E)中，(u,v)代表连接顶点u与顶点v的边，而w(u,v)代表此边的权重，若存在T为E的子集(即)且为无循环图，使得w(T)最小，则此T为G的最小生成树，公式(1)即在计算最小的边权重：

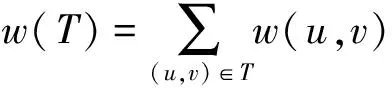
(1)

Kruskal算法假设令最小生成树的初始状态为只有n个顶点而无边的非连通图T=(V,{})，图中每个顶点自成一个连通分量。在E中选择代价最小的边，若该边依附的顶点分别在T中不同的连通分量上，则将此边加入到T中；否则，舍去此边而选择下一条代价最小的边。依此类推，直至T中所有顶点构成一个连通分量为止。因此，此算法根据图形中边的连接分布确定连接所有顶点的最短路径。

1.3 各建筑集群中的太阳能供暖系统设计优化

1.3.1系统原理

在确定建筑集群组成后，针对每个建筑集群建立集中式太阳能供暖系统。本文中太阳能供暖系统架构如图2所示。系统包括太阳能集热器、天然气锅炉(辅助热源)、蓄热水箱、供热管道以及末端负荷。

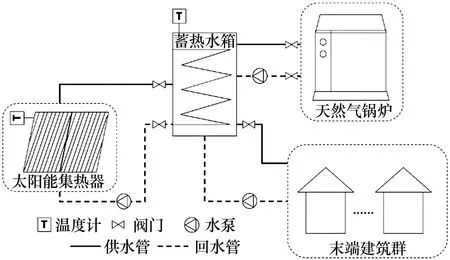
图2 太阳能供暖系统原理

(1)太阳能集热器

在太阳能供暖系统中，平板集热器应用最广泛，其集热量及集热器进、出口水温计算公式[9]为：

QST=3.6AC[FR(τα)eIC-FRUL(Tci-Tα)]

(2)

公式(2)中：QST为集热器集热量，kJ；FR为集热器无量纲热转移因子,无量纲；AC为集热器有效集热面积，m2；(τα)e为集热器有效透过率τ与吸收率α的积，无量纲；IC为太阳能辐射强度，W/m2；UL为集热器总热损失系数，W/m2/℃；Tci为集热器进口温度，℃；Tα为环境温度，℃。

QST=cjmjx(Tco-Tci)

(3)

公式(3)中：Tco为集热器出口温度，℃；cj为集热工质的比热，kJ/(kg·℃)；mjx为集热循环质量流量，kg/h。

太阳能集热器的启停采用温差控制，控制逻辑参考如下所示[10]：

(4)

公式(4)中:TS为水箱水温，℃。

(2)蓄热水箱

本文选用短期蓄热水箱作为储热设施，蓄热水箱水温变化数学表达如下[9]：

(5)

蓄热水箱热损失公式如下：

Qloss(τ)=USVSX(TS(τ)-Ta(τ))

(6)

公式(5)～(6)中:Qloss(τ)为水箱在τ时刻向外界散失的热量水箱散，kJ；US为水箱热损失系数，W·m-3·℃-1；VSX为水箱体积，m3；Cρ为水的比热，kJ/(kg·℃)。

(3)辅助热源

本文采用天然气热水锅炉作为太阳能供暖系统中的辅助热源，其制热量可由公式(7)计算。

Qfr=3600ηfrPfr

(7)

公式(7)中:Qfr为燃气锅炉加热量，kJ；ηfr为燃气锅炉运行负荷率；Pfr为燃气锅炉额定功率，kW。

辅助热源的启停采用温度控制：当水箱温度低于45℃时，辅助热源开启，具体控制逻辑为[9]：

(8)

(4)管道传输热损失

本模型假设热损失量与能量转移成正比，热损失量按每千米管道长度的热量传输值的4.3%[11]计算。

1.3.2目标函数

针对每个建筑集群，以该集群内的集中式太阳能供暖系统全生命周期成本最小为优化目标，目标函数如下式所示：

minLCC=min(CRFyCin+Cop-Crz)

(9)

公式(9)中:LCC为全生命周期成本，元；y为时间系数，a；CRF为资本回收系数；Cin为系统中所有设备的初投资总费用(包括管网建设成本)，元；Cop为系统设备在运行年限内的运行费用，元；Crz为系统设备残值，元。

系统的初投资费用可表示为：

Cin=CcoAco+CsxVsx+CrqPfr+Cq+Cfj

(10)

其中Crq为燃气锅炉单位加热功率成本，元/kW；Cco为太阳能集热器单位价格，元/m2；Aco为太阳能集热器面积，m2；Csx为蓄热水箱单位体积设备费用，元/m3；Cq为管网建设成本，元；Cfj为阀门附件、水泵等成本费用，元。

供暖系统的运行维护费用，是指供暖系统在运行年限内由于设备运转所花费的燃料以及运输费用，本研究中主要为供暖设备消耗天然气的费用，因此系统设备在运行年限内的运行费用：

(11)

公式(11)中:Cfr为燃气锅炉单位热量价格，元/kJ；Qfrz为燃气锅炉的加热量，kJ；MD为电价，元/kWh；SBH为循环泵耗电量，kWh;ζ为设备维修费占设备购置费的比率，取 2%。

系统设备残值计算如下式所示：

Crz=Cinr

(12)

公式(12)中：Crz为固定资产净残值是指固定资产使用期满后，残余的价值减去应支付的固定资产清理费用后的那部分价值；r为固定资产净残值占固定资产原值的比例，简称净残值率，一般在 3%～5%:[12]，本文取 4%。其中资本回收系数计算如下：

(13)

公式(13)中：i为年利率，取 8%；y为系统使用年限，取 15 a[13]。

1.3.3约束条件

(1)等式约束

针对每个建筑集群，太阳能供暖系统在运行阶段的逐时供给热量应与集群内所有用户的逐时所需热量相等，数学表达式如下：

Qhx(τ)+Qfrt(τ)-Qloss(τ)-Qsx(τ)=Qf(τ)

(14)

公式(14)中：Qhx(τ)为集热器在τ时刻的蓄热量，kJ；Qfrt(τ)为天然气锅炉在τ时刻供给的热量，kJ；Qloss(τ)为水箱在τ时刻向外界散失的热量，kJ；Qsx(τ)为水箱在τ时刻所蓄存的热量，kJ；Qf(τ)为建筑群在τ时刻热需求量，kJ。

(2)不等式约束

系统不等式约束条件包括集热器面积约束，储热水箱体积约束，燃气锅炉额定功率约束以及水箱运行温度约束，具体表达如下所示。

0≤Aco≤Amax

(15)

0≤Vsx≤Vmax

(16)

(17)

40℃≤TS≤85℃

(18)

公式(15)～(16)中:Aco为集热器面积，m2；Vsx为储热水箱体积，m3；Qfh为建筑集群某一小时的最大热负荷值，kW；TS为水箱运行温度，℃。约束值设定如表1所示。

表1 约束条件参数设定

(3)初始状态设定

在初始时刻，蓄热水箱内水温取 45 ℃，集热器内部工质温度取10 ℃

Ts(τ=1)=45,Tco(τ=1)=10,Tci(τ=1)=10

(19)

表2 系统模拟计算参数设定

遗传算法是一种较为成熟的优化算法，它提供了一种求解复杂系统优化问题的通用框架，不依赖于问题具体的领域，对问题的种类有很强的鲁棒性，所以在组合优化，机器学习等诸多领域都有广泛应用。在本研究中针对农村地区的建筑群，进行基于建筑聚类的太阳能供暖系统设计优化，面对本研究中多种建筑群聚类情况，遗传算法通过模拟自然进化过程中搜索最优解的形式来寻找最适合农村当地建筑群，生命周期成本最低的太阳能供暖系统优化设计形式。

本研究针对的对象是偏远农村地区的建筑，对建筑群进行聚类分析，并进行集中-分散组合式太阳能供暖系统的优化设计研究，太阳能供暖系统中各子系统均为成熟模型，但实验平台搭建与数据获取较为困难，不足以进行对比分析。

基于此，模型采用遗传算法在MATLAB环境中求解，以1 h为时间步长，整个采暖季(11月1日至次年3月31日)为计算周期。优化变量包括太阳能集热器面积(ACO)、蓄热水箱容积(VSX)、以及燃气锅炉运行功率(Pfr)。遗传算法初始化种群大小设为 150，迭代次数设为 20。

1.4 最优建筑群聚类方案及最优系统设计比选

通过密度聚类分析得到多种由不同建筑集群组成的聚类方案后，可针对每种方案中的各建筑集群分别进行太阳能供暖系统设计优化，计算每个建筑集群太阳能供暖系统的全生命周期成本，每种建筑群聚类方案的太阳能供暖系统总全生命周期成本即为各建筑集群太阳能供暖系统全生命周期成本的累加值。全生命周期成本累加值最低的方案即为最优建筑群聚类方案，相对应的系统设计即为最优“集中-分散”组合式太阳能供暖系统形式。

2 结果与分析

2.1 案例分析

准确的负荷预测是建筑的供暖系统优化设计的基础[16]。本文以西藏某典型农村地区为例，选取当地冬季供暖典型设计日(1月17日)建筑热负荷模拟结果进行分析。典型建筑共两层，建筑面积131.76 m2。利用TRNSYS模拟生成3种主要建筑热负荷类型，分别是全天有人在室(人员在室时间00:00-24:00)的居住建筑热负荷(类型1)，白天人员外出(人员在室时间18:00-次日08:00)的居住建筑热负荷(类型2)，以及白天有人在室(人员在室时间08:00-18:00)的办公建筑热负荷(类型3)。根据《居住建筑节能设计标准》，西藏地区的供暖计算换气次数取0.5次h-1，冷风渗透系数取0.2次h-1，住宅仅卧室与起居室供暖，楼梯间均不供暖。采暖室内设计温度设定为15℃可基本满足人们日常工作和生活需要。照明功率密度取6 W/m2，设备功率密度取3.8 W/m2，人员按卧室2人、客厅3人设定。根据DBJ 540001-2016《西藏自治区居住建筑节能设计标准》和JGJ 26-2010《严寒和寒冷地区居住建筑节能设计标准》设定建筑外围护结构参数，窗体结构采用的是双层中空玻璃，传热系数为2.88 W/(m2·K)。典型日内3种建筑逐时热负荷如图3所示。

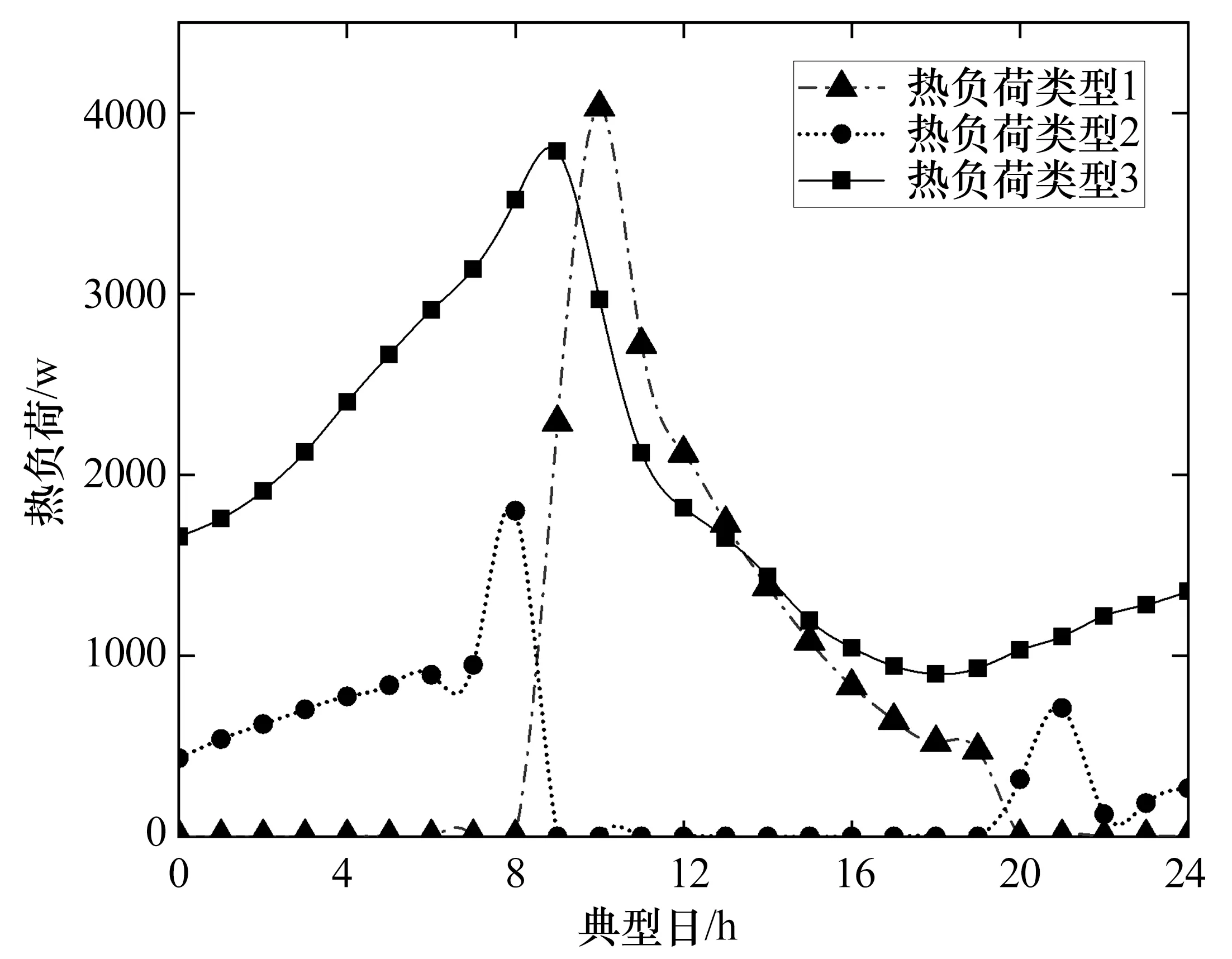
图3 典型日热负荷

以某农村建筑空间布局为例，将以上3种热负荷特性随机分配给该农村18栋建筑，分配结果如图4所示。图中每点代表一栋建筑，不同颜色代表其热负荷特性不同。通过调用DBSCAN密度聚类方法，在邻域半径范围(26～54 m)以及最小样本数范围(1～16)内进行等距离调节，得到8种互不重复的建筑群聚类方案，聚类结果如图5所示。图中，不同聚类方案按照建筑聚类数量的升序排列顺序被依次命名为A、B、…、H，不同颜色用以区分不同建筑群聚类。空心点表示该建筑独立代表一个建筑集群，采用单户式太阳能系统进行建筑供暖。

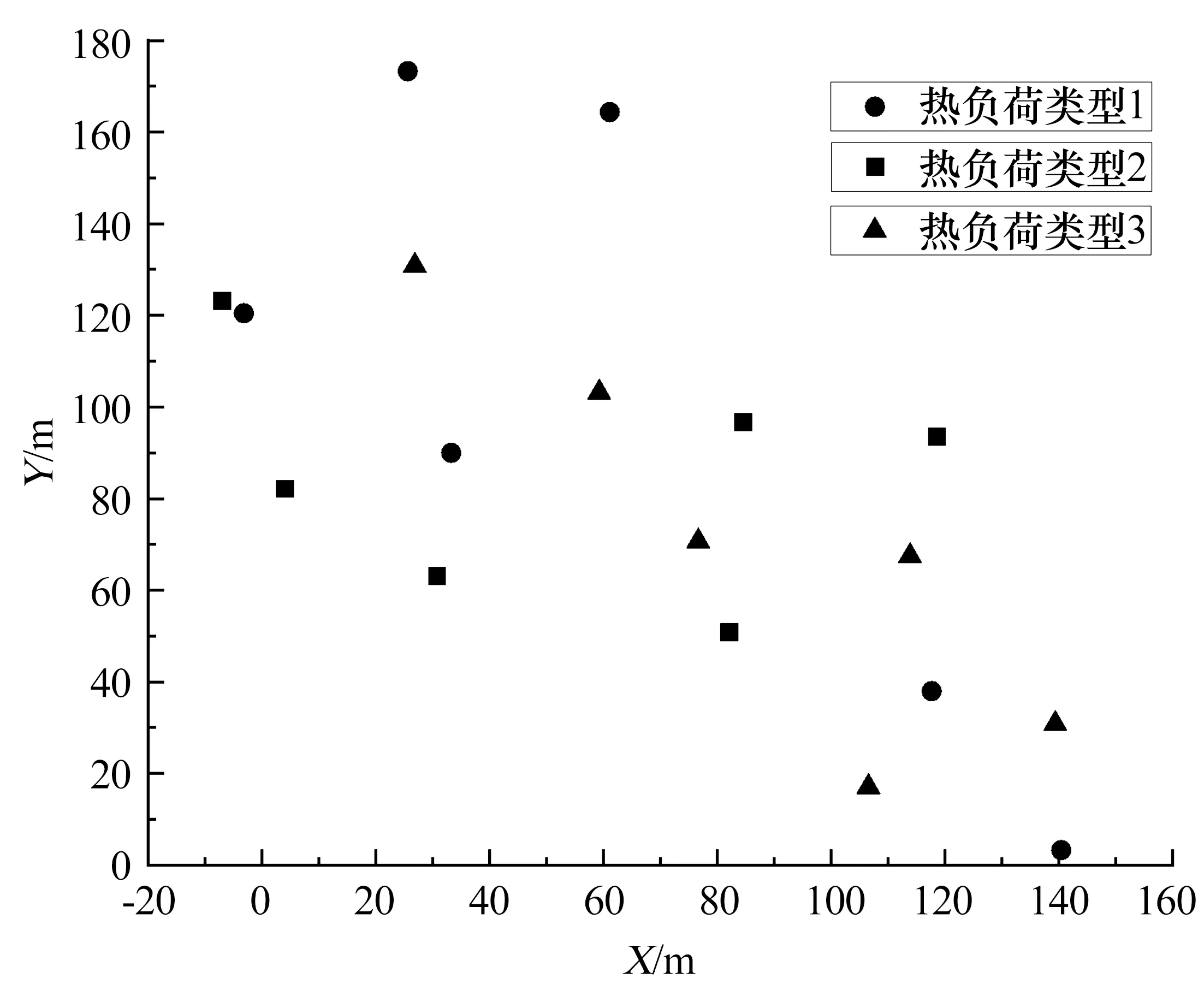
图4 区域建筑分布

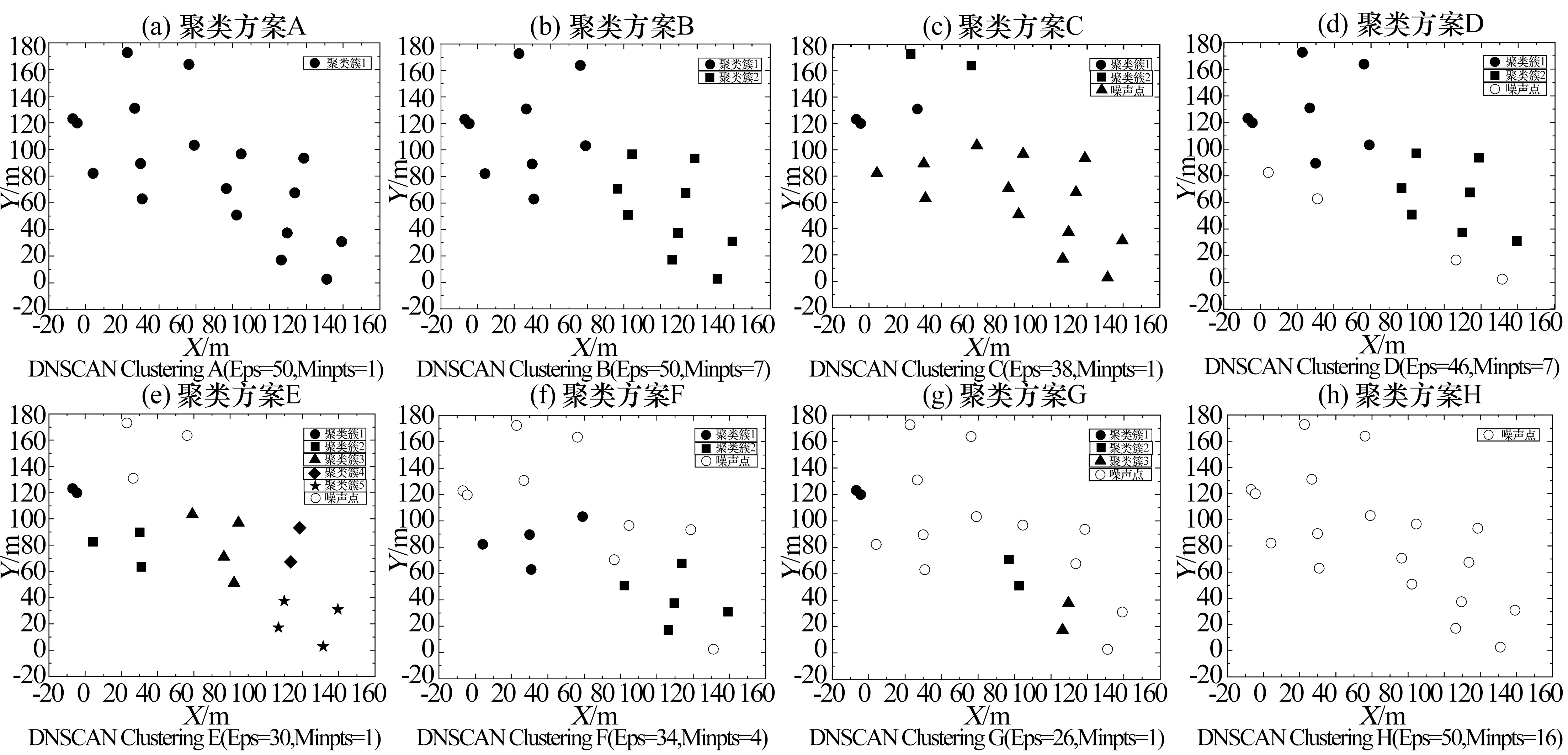
图5 不同聚类方案下的建筑群空间分布

2.2 结果分析

在8种建筑聚类方案下进行“集中-分散”组合式太阳能供暖系统设计优化，结果如图6所示。由图6可以看出，随着建筑集群数量的增多(聚类方案由A到H)，“集中-分散”组合式系统总集热器面积逐渐增加，总水箱体积与总燃气锅炉额定功率呈现先减少、后增加的变化趋势，管道长度持续减小。究其原因，聚类方案由A向C变化时，建筑集群数量由1增加到3，建筑集群规模及供热管网长度减小，管道成本和热量传输损失降低，水箱体积和燃气锅炉额定功率有所减少；当聚类方案由D向H变化时，越来越多的单户式供暖形式出现，由于每套系统仅用于满足单户供暖需求，集热器与水箱的富余容量逐渐增加，导致系统的产热设备容量有所增加。随着建筑集群数量的增加，集群内部建筑间距减小，供热管道长度呈持续减小趋势。

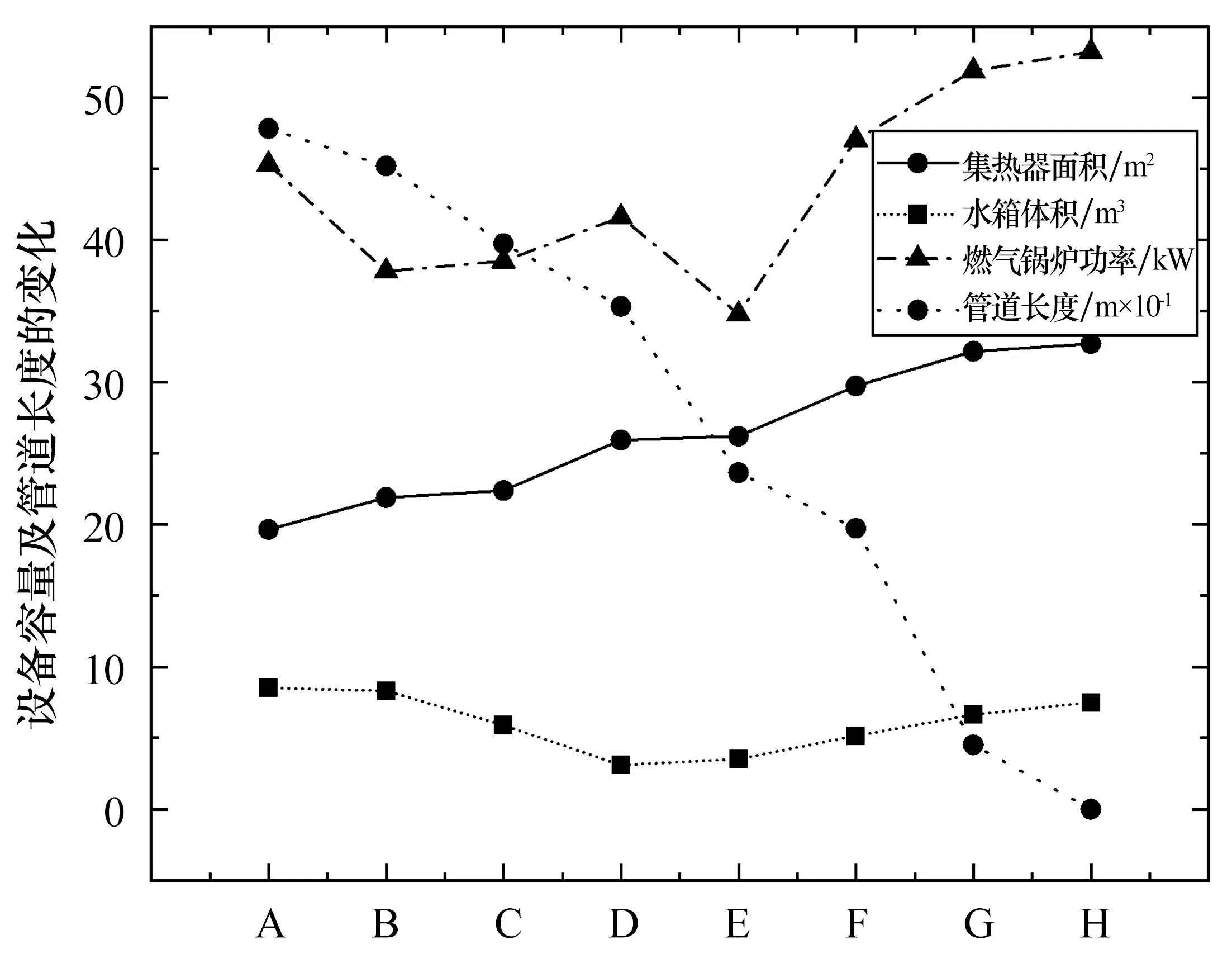
图6 各聚类方案下“集中-分散”组合式太阳能供暖系统总产热设备容量及管道长度变化

根据图6可知，虽然除管道之外的其它设备随建筑集群数量的增加或先减少后增加，或持续增加，但管道长度却是持续下降的。图7为不同建筑群聚类方案下的系统全生命周期成本及其分解。由图7可知，方案H(建筑集群数量最多)下“集中-分散”组合式太阳能供暖系统全生命周期成本最低(17.58万元)，系统全生命周期成本随建筑集群数量的增多呈持续减小趋势，变化趋势与管道长度变化趋势相同。通过对图7中系统全生命周期成本的分解分析可以发现，管道成本对于系统全生命周期成本的影响巨大，且这种影响是显著大于其它设备容量变化对系统全生命周期成本的影响。整体来看，通过建筑聚类对区域太阳能供暖系统进行“集中-分散”的组合式划分，可以有效减少系统中除供热管道之外的其它设备容量，但却会增加供热管道长度。因此，建筑集群划分能否降低区域供暖系统全生命周期成本高度取决于供热管道成本的占比大小，而管道价格对于管道成本比例的影响至关重要，需要进行相应的敏感性分析。

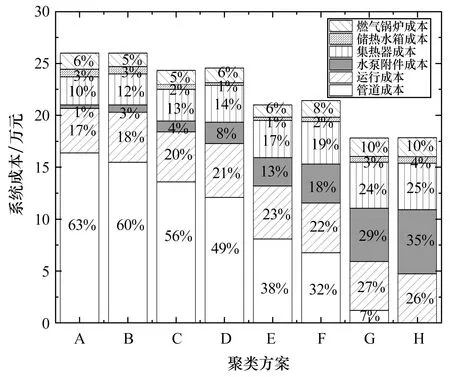
图7 各聚类方案下系统全生命周期成本的变化

2.3 敏感性分析

根据上述分析可知，供热管道价格会显著影响聚类方案的选择，进而影响太阳能供暖系统设计。为研究管道单价变化对太阳能供暖系统形式设计的影响，设计管道价格50、100、150、200、250、300、350元/m共7种工况，对比分析得出各种管道价格下系统在不同建筑群聚类方案下的系统全生命周期成本，结果如图8所示。

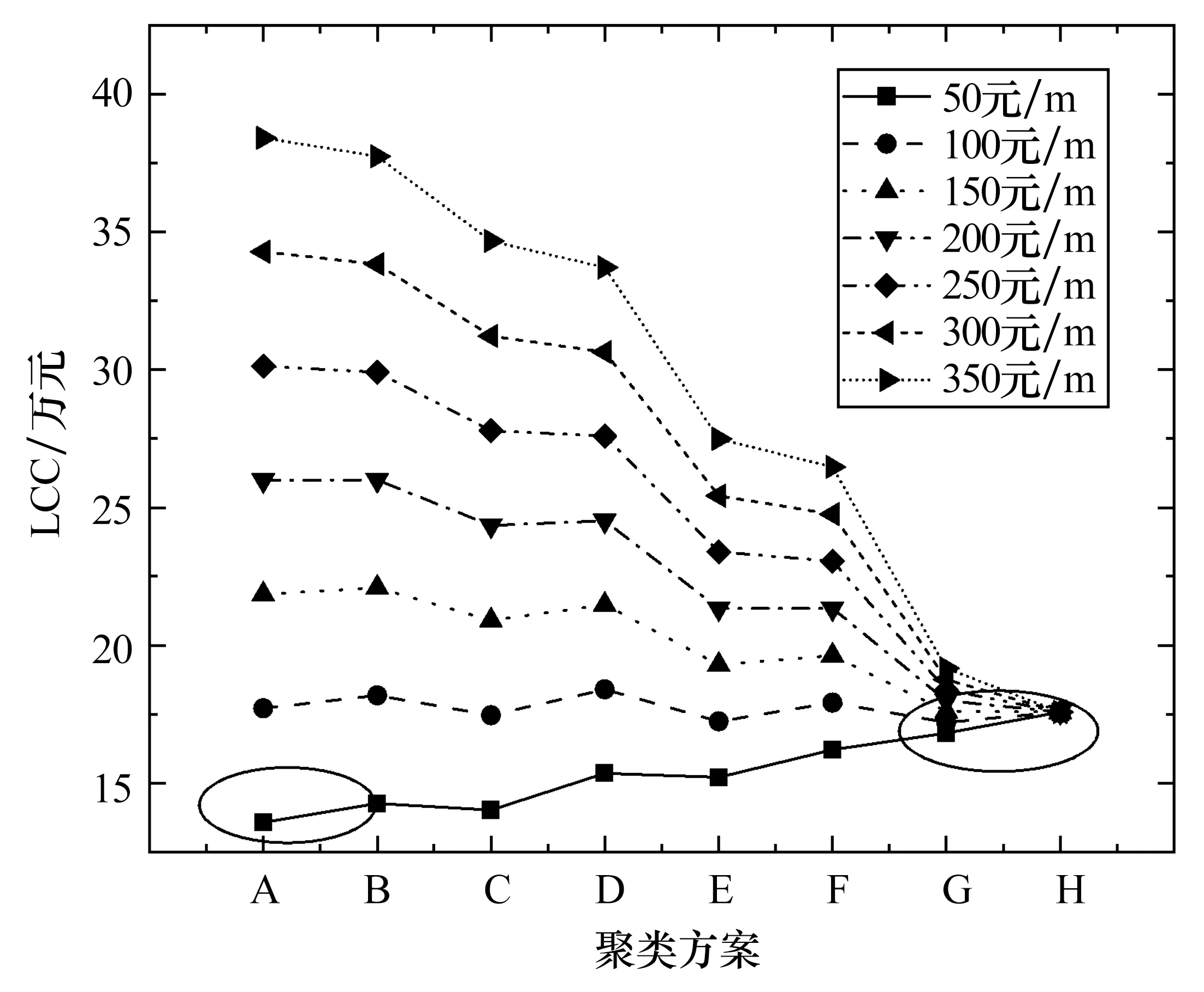
图8 不同建筑聚类方案下系统全生命周期成本随管道价格的变化

由图8可知，供热管道价格对于最优建筑聚类划分选择具有明显的影响作用。聚类方案H下，各个单体建筑独立供暖，不存在管道成本，系统全生命周期成本在不同供热管道价格下均保持不变。管道价格在100元/m时，不同的建筑聚类方案对于供暖系统总成本的影响较小，可作为判断当地是否适合进行“集中-分散”组合式太阳能供暖系统设计的价格阈值：当管道价格高于100元/m时，建筑聚类虽能降低产热设备成本，却增加了供热管道成本，整体上系统全生命周期成本增加，使得系统成本最低的聚类方案在不同管道价格下均为建筑完全分散的方案H，没有进行建筑聚类的必要；当管道价格低于100元/m时，不同建筑聚类下的系统设计优化结果差异性较为显著，如管道价格为100元/m时，系统成本最低的聚类方案为方案G(图中画圈处)。本文模型中管道价格阈值约为100元/m，但此值的确定与具体案例密切相关。由于不同地区的气候资源、建筑布局、建筑负荷均会对结果产生一定影响，需要根据当地情况展开分析研究，以确定建筑聚类方案、系统最优设计以及管道价格阈值。

3 结 论

本文提出了一套区域建筑集群DBSCAN聚类分析方法以形成多种建筑聚类方案，并建立了“集中-分散”组合式太阳能供暖系统优化模型，为每种聚类方案提供各自对应形式的太阳能供暖系统，形成结论如下：

(1)建筑集群数量的增加导致“集中-分散”组合式太阳能供暖系统总管道长度逐渐较小，总集热器面积逐渐增加，系统总水箱体积与总燃气锅炉额定功率呈现先减少、后增加的变化趋势。

(2)“集中-分散”组合式太阳能供暖系统全生命周期成本变化趋势与供热管道成本变化趋势一致。供热管道价格对于最优建筑集群划分具有显著影响。

(3)可通过管道价格阈值判断是否需要进行“集中-分散”组合式太阳能供暖系统设计。当管道价格高于阈值，无需进行建筑聚类，采取完全分散的单户式太阳能供暖最为经济；当管道价格低于阈值，需要在不同聚类方案下对区域整体太阳能供暖系统进行优化设计，以选择最优建筑聚类方案。

本文在模型验证过程中选取某一典型农村的建筑布局进行案例分析，后续研究中将通过调整建筑布局加强结果的适用性分析，并根据区域中建筑聚集程度计算出相应管道价格阈值。