风速、湿度及汗湿量对服装热阻影响的试验

柳光磊,刘何清,唐炫,吴世先,吴国珊

(1.湖南科技大学 资源环境与安全工程学院, 湖南 湘潭 411201;2.兴义民族师范学院 物理与工程技术学院,贵州 兴义市 562400)

服装的热阻是衡量服装热舒适性的重要标准,它由基本热阻和服装外表面边界空气层的热阻组成并受多种因素影响,每种因素对热阻的影响都是一个复杂的过程.

目前国内外主要从构建模型、试验、数值模拟3个方面开展服装热阻的研究.Fanger[1]在1970年建立着装人体在稳态条件下能量平衡的热舒适性方程;周俊彦[2]建立环境风速和温度的热舒适组合模型;Wan[3]引入服装的热湿传递到二节点模型来预测人体生理反应;于瑶[4]分析风速与步速对服装表面空气层热阻的影响并得出服装的热阻与风速及步速的关系公式;李敏[5]研究了服装热阻的计算方法;张文欢[6]研究了服装局部热阻与总热阻的动静态关系及其模型;Joshi[7]考虑身体运动因素建立了服装热传递模型;周俊彦[8]开展了热舒适条件下环境风速和温度最佳组合的试验研究;Ueda[9]研究了织物透气性对服装通风的影响;赖军[10]研究了风和人体运动对服装动态热阻的影响;Oh[11]研究了风速和风向对人体散热的影响;Ismail[12]研究了环境条件对潜热和显热损失的影响以及步行和风速对热阻的影响;胡紫婷[13]研究了衣下空气层对透气型防护服热阻和湿阻的影响;杨恩慧[14]研究了矿工服湿润程度对其热阻的影响;Liu[15]研究了服装热阻与操作温度对皮肤温度的影响;Wang[16]研究了服装空气层与湿阻的关系;Tu[17]研究了有风环境下透水织物的有效热阻;Mao[18]对服装系统进行了热湿传递数值模拟;Zhang[19]对手部对流传热系数及风速影响的数值模拟;Shen[20]对多孔纺织品进行了传热和流动的数值模拟.

目前的研究多关注服装本身因素、环境因素对服装热阻的影响,但关于风速、湿度及汗湿量对服装热阻影响的研究不多,仍然需要进一步研究.本文借助自制暖体假人平台,选取矿工服面料和绒衣,分别在不同的风速、湿度及汗湿量的状态下进行服装热阻的测定试验,为矿井工人热舒适评价提供参考.

1 研究方法

1.1 服装热阻

为了研究环境湿度、风速及汗湿量对服装热阻的影响,必须清楚服装热阻的测定方法和计算方法,并且明确服装在人与环境的热交换中的计算模型和服装热阻的影响因素.

1.1.1 服装热阻的测定方法和计算方法

本试验装置是基于“铜人模型”自制暖体假人.测定的方法:通过测量电能的消耗计算出服装的热阻值.在测定过程中,暖体假人表面温度维持在33 ℃.

测定服装热阻,要明确3种不同概念的服装热阻的计算方法[21-22]:

1)总热阻It(从人体皮肤表面到环境的热阻)

(1)

式中:It为服装总热阻, m2·℃·W-1;tsk为皮肤表面平均温度,℃;ta为环境空气温度,℃;H为人体皮肤表面到环境的热流密度, W·m-2.

2)有效热阻Icle(从人体皮肤表面到服装外表面的热阻)

Icle=It-Ia.

(2)

式中:Icle为服装的有效热阻, m2·℃·W-1;Ia为裸体铜人表面空气层的热阻, m2·℃·W-1.

为了得到Ia的值,可以对裸体暖体假人在相同的环境条件下做测定,并利用式(1)计算.

3)基本热阻Icl(从人体皮肤表面到服装外表面的热阻,并考虑到服装面积因素的影响)

Icl=It-Ia/fcl.

(3)

式中:Icl为基本热阻,m2·℃·W-1;fcl为服装面积系数,是着装的人体表面积与裸体表面积之比.

1.1.2 服装在人与环境的热交换中的计算模型

1970年, Fanger提出了描述着装人体在稳态条件下能量平衡的热舒适性方程[23-24]，如式(4)所示.

M-W-3.05[5.733-0.007(M-W)-Pa]-0.42(M-W-58.15)-0.017 3M(5 867-Pa)-

(4)

式中:M为活动量(能量代谢率),W·m-2;W为人体对外所做的机械功,W·m-2;Pa为人体周围空气中的水蒸气分压,kPa;tcl为着装人体外表平均温度,℃;Icl为成套服装基本热阻,m2·K·W-1;hc为人体外表与环境的对流换热系数,W·m-2·K-1;Tcl为着装人体外表平均温度,K;Tr为环境的平均辐射温度,K.

环境与人体的中介即服装的基本热阻,它虽然没有直接反映在热平衡方程中,但它直接影响服装的特性系数.本试验通过调节风速改变对流换热系数hc,通过调节相对湿度改变人体周围空气的水蒸气分压,通过调节服装的汗湿量改变从人体带走的蒸发热量.

1.1.3 服装综合热阻的定义

边界层的概念对于表面与流过表面的流体之间的对流传热和传质有重要意义.服装表面的速度边界层结构如图1所示(U0表示主流速度,x表示流体在平板上沿流动方向流动的长度,y表示边界层厚度,xcr表示边界层的临界长度,δ0表示层流底层厚度),与速度边界层类似,热和浓度边界层沿流动方向是增大的.

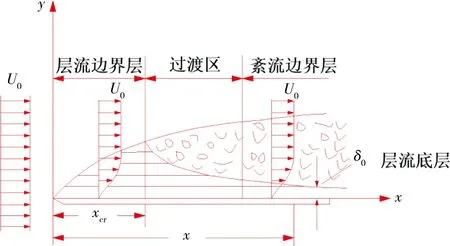
图1 服装表面速度边界层结构

服装在人体热平衡过程中起到保温和阻碍湿扩散的作用.服装的存在影响了皮肤表面的汗液蒸发.一方面服装对皮肤表面的水蒸气扩散有一个附加的阻力,另一方面服装吸收部分汗液,使得只有剩余部分汗液蒸发冷却皮肤.服装借助毛细现象吸收和传输汗液,这部分汗液不是在皮肤表面蒸发,而是在服装表面或服装内部蒸发,这样就形成了水蒸气的浓度梯度,通过水蒸气的浓度梯度得出“湿阻”公式.

(5)

式中:Iet为服装湿阻,Pa·m2·W-1;psk为皮肤温度对应的饱和水蒸气分压,Pa;q为热流密度,即假人与外界进行热湿交换的单位面积上的总功率,W·m-2.

本文给出“服装综合热阻”定义,它是指服装两侧的温度差与热流密度之间的比值.

(6)

式中:Rcomp为服装的综合热阻, m2·℃·W-1;Δt为服装两侧的温差,℃;q为热流密度(单位时间内通过物体单位横截面积上的热量),W·m-2.

1.2 试验方案与系统

本试验对不同环境相对湿度、风速条件下的工作服热阻进行测量,得出热阻随湿度、风速变化的规律.

1.2.1 试验方案

环境温湿度及风速的变化会影响服装外表面空气层的对流及辐射散热,从而影响服装热阻.通过暖体假人试验研究环境温度、湿度及风速对干湿矿工服热阻的影响.

图2 试验所用服装面料和绒衣

试验服装采用纯棉布料和矿工绒衣,试验所用服装面料和绒衣如图2所示.其中编号01,02为厚度不同的纯棉服装面料,03为绒衣.

试验工况:环境温度19,21,23 ℃,假人表面温度33 ℃,风速小于0.1 m/s,每组试验进行1 h,前30 min用来稳定假人皮肤表面温度,待假人表面温度稳定后,测量后30min内的假人消耗功率,利用式(1)计算总热阻.

试验分为3个阶段,每个阶段中暖体假人的表面温度均保持33℃.第一阶段研究服装外表面热阻,环境温度为19,21,23 ℃,风速小于0.1 m/s,每种环境温度下测量5次,取平均值;第二阶段研究湿度对服装热阻的影响,环境温度为33±0.4 ℃,风速小于0.15 m/s,环境相对湿度为50%,60%,70%,80%,90%及100%;第三阶段研究不同环境风速对服装热阻的影响,环境温度为30 ℃,湿度为90%,环境风速为0.5,1.0,1.5,2.0,2.5 m/s.

1.2.2 试验系统

本试验在人工环境舱进行,试验中测量的环境参数为温度(ta),湿度(RH),风速(vwind),测量服装质量:干服装质量(mdry),湿服装质量(mwet),测量不同工况下的服装表面热阻(Ia)和服装总热阻(It).

1)试验平台

试验在湖南科技大学资源环境与安全工程学院人工环境舱内进行.舱内的温度、湿度用监测监控程序动态调控,舱内密封性可满足试验要求.其中,舱的温度调控范围为-15～50 ℃,精度±0.5 ℃;湿度调控范围为30%～95%,精度±2%.环境因素对服装热阻的影响试验平台如图3所示.

1-TSI-5725手持式叶轮空气流速仪;2-温湿度手持式仪表(HMP76、77探头);3-万特电子天平;4-一等标标准水银温度计;5-暖体假人

2)环境影响因素和服装质量测量仪器与参数

环境参数主要是测量人工环境舱内的ta,RH,vwind,测量服装质量mdry,mwet.仪器和参数见表1.

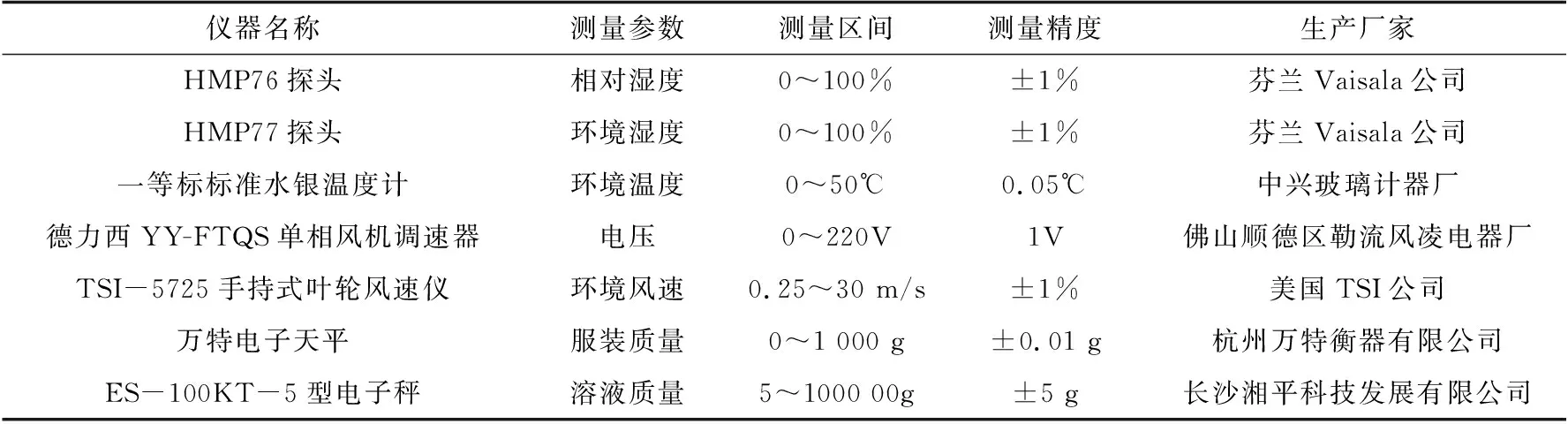
表1 环境影响因素和服装质量测量仪器与参数

试验步骤如下:

1)试验准备,打开人工环境舱电源及监控仪器,调控环境舱的热湿环境参数,直至达到所需的试验工况,当试验工况稳定时,为减少试验误差,用一等标准水银温度计、温湿度手持式仪表及TSI-5725式风速测量仪对舱内试验工况进行核实.

2)试验开始,将干燥的服装、绒衣放置在设置好的环境舱(环境温度为21 ℃、湿度为50%、风速<0.15 m/s)内12 h,保证其完全干燥.由于服装贴于假人表面时间较长,每测完一组数据,需要将其取下置于环境舱内,将服装冷却后才能进行第二次试验,每种工况服装测量3次,取3次测量值的均值.

3)当假人皮肤温度达到设定温度并保持稳定30 min后,将完全干燥的服装穿在暖体假人外表面,保证完全覆盖,用安捷伦设备记录30 min内暖体假人消耗功率,试验过程中,保持暖体假人表面温度及环境参数的稳定.

4)重复步骤(1),将环境舱内环境工况调至所需的试验工况,测量服装面料和绒衣在不同环境温湿度及汗湿状态下的热阻.记录不同汗湿状态下服装蒸发所消耗水分(使用电子天平对试验前后的汗湿服装进行称重)以得到蒸发散热量.

5)试验结束,数据传输至笔记本电脑,关闭暖体假人试验平台.

2 试验结果分析

2.1 干服装总热阻

试验利用暖体假人测量服装外表面的空气层热阻.环境温度为21 ℃,暖体假人表面温度33 ℃,风速小于0.15 m/s,试验面料01,02及绒衣03的总热阻测量值见表2.

表2 服装面料01,02及绒衣03的总热阻测量值

2.2 服装外表面热阻

试验利用暖体假人测量服装外表面的空气层热阻.环境温度分别为19,21,23 ℃,暖体假人表面温度为33 ℃,风速小于0.1 m/s,不同环境温度下服装外表面热阻值见表3.

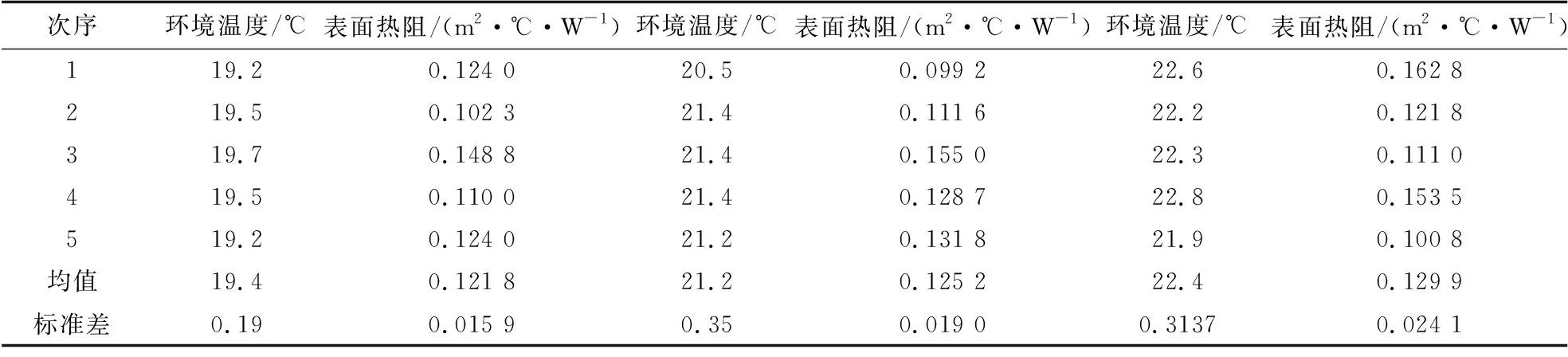
表3 不同环境温度下服装外表面热阻值

从表3可以看出：在3个环境温度条件下测得的假人裸体空气层热阻均值基本接近,个别值存在较大的偏差,分析其原因可能是试验时环境舱门未能紧闭,造成少量空气流入舱内,影响假人皮肤表面与周围环境的对流换热,从而导致假人裸体空气层的热阻发生改变.

2.3 不同湿度条件下服装总热阻

试验利用暖体假人测定湿度对矿工服的影响,为研究相对湿度与新矿工服面料热阻的关系,相对湿度分别定为50%,60%,70%,80%,90%,100%.环境温度30 ℃时不同相对湿度下总热阻如图4所示.

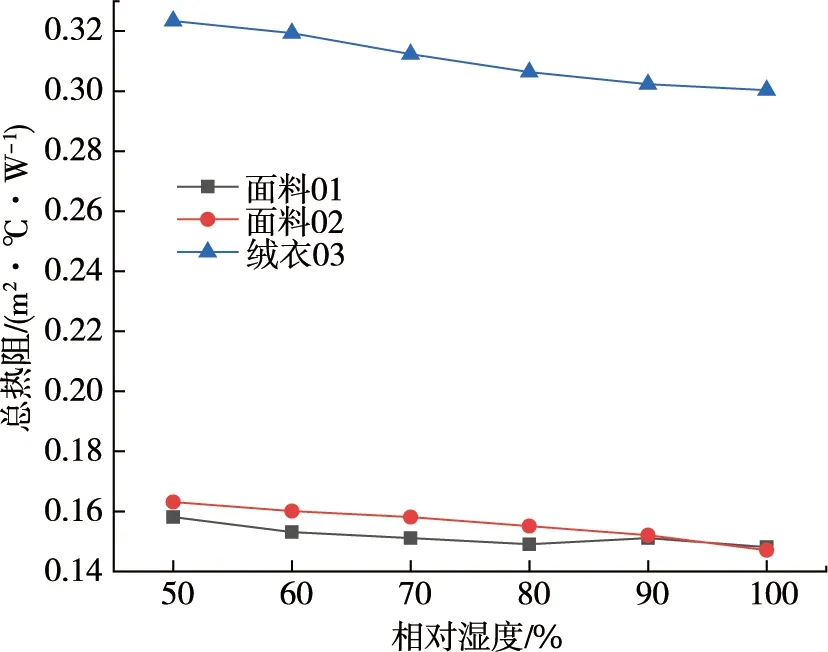
图4 环境温度30 ℃时不同相对湿度下总热阻

从图4可以看出:相对湿度对服装热阻有一定的影响.当环境温度不变时,随着相对湿度的增加,服装热阻呈现减小的趋势.原因如下:空气中存在许多气相水分,气相水分会使得织物纤维的弹性变差,对热阻影响不明显;但当相对湿度变得较大时,会出现液相水分,它会进入织物纤维之间的空隙,并把纤维中的静止空气、死腔空气挤出,从而降低服装的总热阻.

2.4 不同风速条件下服装总热阻

2.4.1 干服装总热阻与风速之间的关系

试验测定环境风速对干燥矿工服面料和绒衣总热阻的影响,环境温度设定30 ℃,调整风流速度,分别为0.5,1.0,1.5,2.0,2.5 m·s-1.环境温度30 ℃时不同风流速度下的总热阻如图5所示.

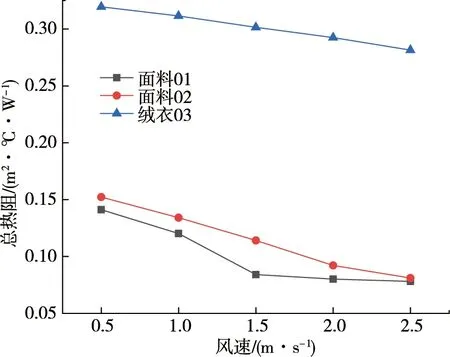
图5 环境温度30℃时不同风流速度下总热阻

从图5可以看出:随着风流速度的增加,干服装总热阻呈现下降趋势.原因如下:

1)风流速度影响了服装的表面空气层热阻,风流的扰动,使得服装表面的静止空气被扰乱,压缩了边界空气层厚度,影响了服装的含气量,从而使服装的总热阻下降.

2)风流速度会从服装气孔及空间渗透到服装内部,扰动里面的静止空气与死腔空气,加强服装开口部位内外空气层之间的对流换热,同时,风流压缩服装,改变服装内空气层的厚度,使得热阻下降.

2.4.2 汗湿服装总热阻与风速之间的关系

试验测量了服装的总热阻.控制服装面料、绒衣的汗湿程度(汗湿量不同),利用电子天平对不同汗湿程度的服装面料进行称重来保证每次试验时服装面料及内衣的含水量一致.环境温度30 ℃、不同汗湿量条件下不同风流速度时的面料总热阻见图6;环境温度30 ℃、不同汗湿量条件下不同风流速度时的绒衣总热阻见图7.

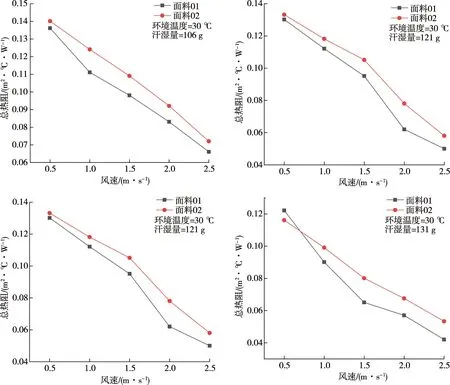
图6 环境温度30℃、不同汗湿量条件下不同风流速度时的面料总热阻

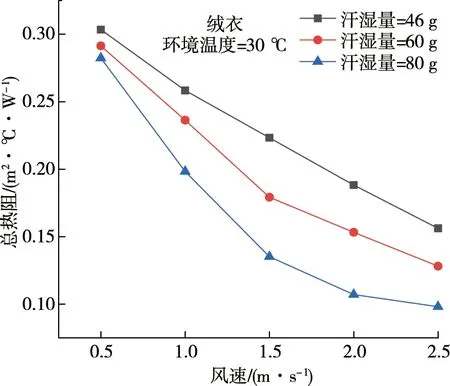
图7 环境温度30℃、不同汗湿量条件下不同风流速度时的绒衣总热阻

从图6和图7可以看出:

1)不论服装处于完全汗湿状态还是其他汗湿程度,其总热阻均随着环境风速的增加而呈现减小趋势.

2)服装的汗湿程度越小,其热阻随风速变化的速率就越小,这是由于汗湿程度越小,此时风流的扰动会使得人体的蒸发散热量与对流散热量同时增加,从而使得热阻减小.

3 讨论

3.1 服装外表面热阻

当环境温度为舒适温度21 ℃时,穿着衣服的人的正常皮肤表面温度为33 ℃,衣服内外的温差为12 ℃,传热量为43.5 W/m2,则传热热阻为0.275 m2·℃/W (单位面积传热量=传热温差/传热热阻),衣服外表面有一层空气层,这层空气层的热阻大约为0.12 m2·℃·W-1(0.774 clo),所以服装所具有的热阻值为0.275-0.12=0.155 m2·℃·W-1,由此,把1clo定义为0.155 m2·℃·W-1,热阻的倒数为传热系数[17].

表面热阻与风速的关系见表4,说明风速对对流换热系数影响较大,是热交换的重要因素.

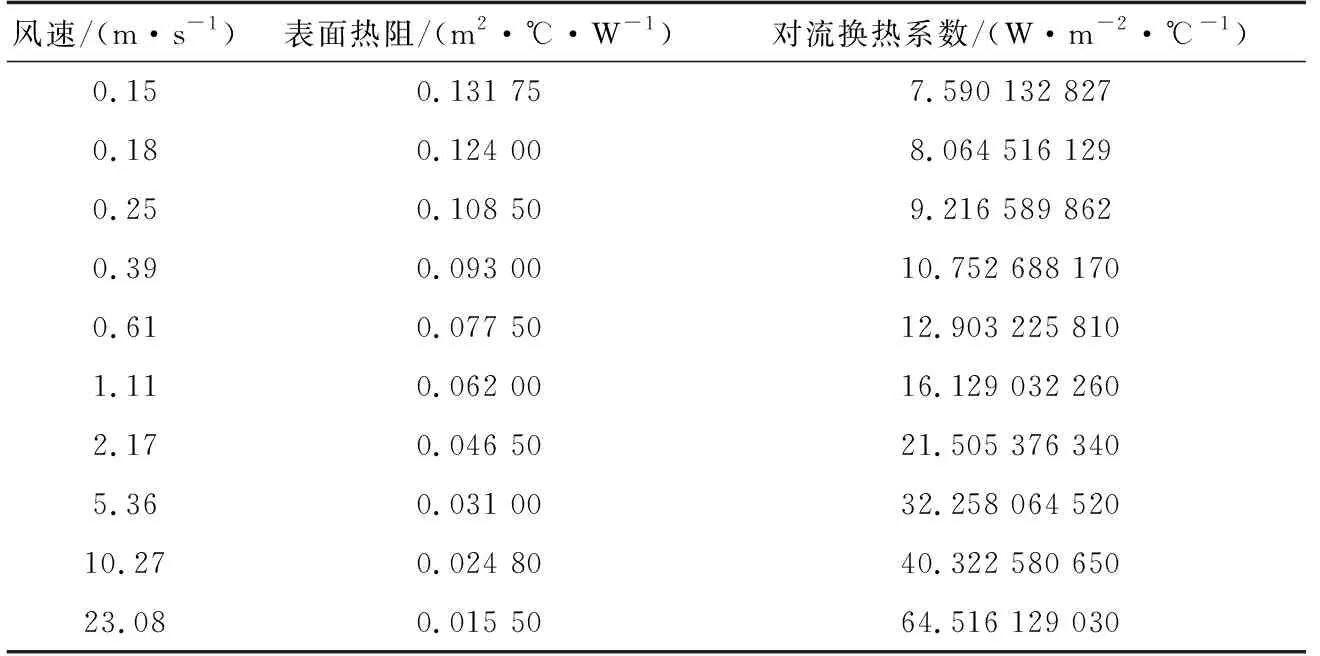
表4 表面热阻与风速的关系[19]

本试验中,假人表面温度33 ℃,风速小于0.1 m/s,在环境温度为19.4,21.2,22.4 ℃测得的表面热阻分别为0.121 8,0.125 2,0.129 9 m2·℃·W-1,与环境温度为舒适温度21℃下的服装外表面空气层的热阻0.12 m2·℃·W-1还存在一定的试验误差,但误差不大.

表面热阻与风速的关系如图8所示,其表达式为

Ia=0.062 95v-0.395 13.

(7)

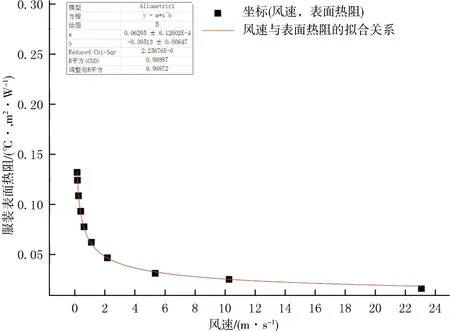
图8 风速与服装表面热阻的关系

3.2 环境风速对服装表面热阻的影响

环境风速主要影响服装的表面热阻,从而使服装的总热阻明显下降.在低风速下,服装保暖性能的降低主要是由于表面热阻减小,而在高风速下,对流、渗透及压缩的影响程度增加.有时人感到冷风“吹透”了服装,实际上并不是冷空气真的透过服装织物进入内部,而是表面热阻下降、服装被压缩、使局部散热量增大而带来的冷感.

试验中风速为0.5～2.5 m·s-1,是在低风速下进行,不考虑风压缩局部服装改变服装内空气层的厚度,服装的有效热阻Icle不变,服装总热阻的降低主要是由于表面热阻减小了.

试验得出了在环境温度21℃、暖体假人表面温度33℃及风速小于0.15 m·s-1下面料01,02及绒衣03的总热阻测量值分别为0.160,0.173,0.345 m2·℃·W-1,空气层的热阻大约为0.12 m2·℃·W-1,根据式(2)得出面料01,02及绒衣03的有效热阻分别为0.040,0.053,0.225 m2·℃·W-1,由试验数据根据式(2)得到表面热阻与风速的值见表5,风速与服装表面热阻的关系如图9所示.

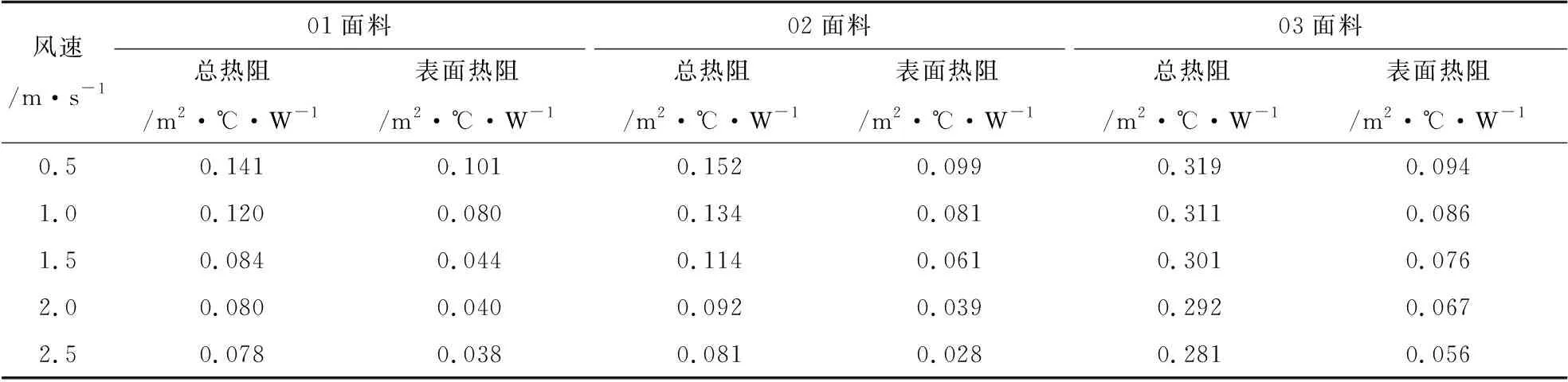
表5 试验得到的表面热阻与风速的值

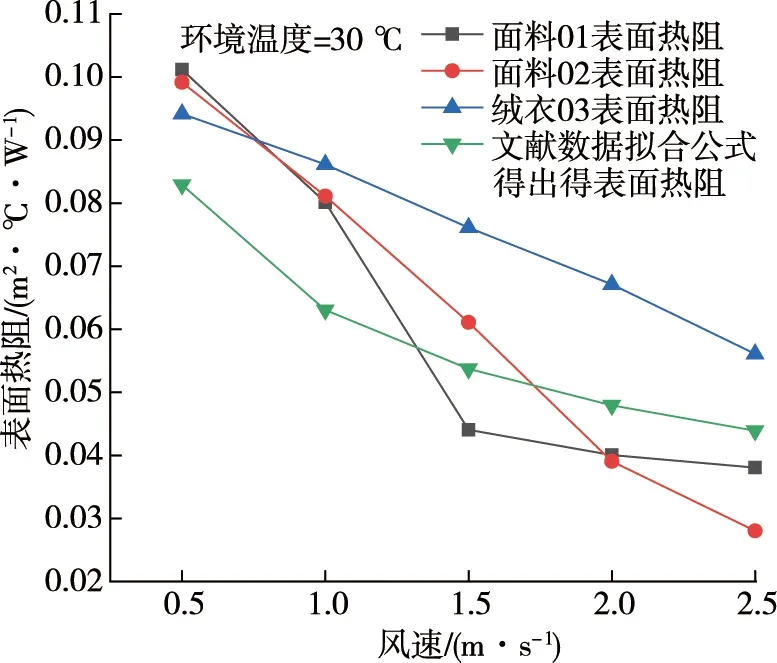
图9 风速与服装表面热阻的关系

作者将试验获得与文献[19]得出的数据,拟合出的公式如图10所示.

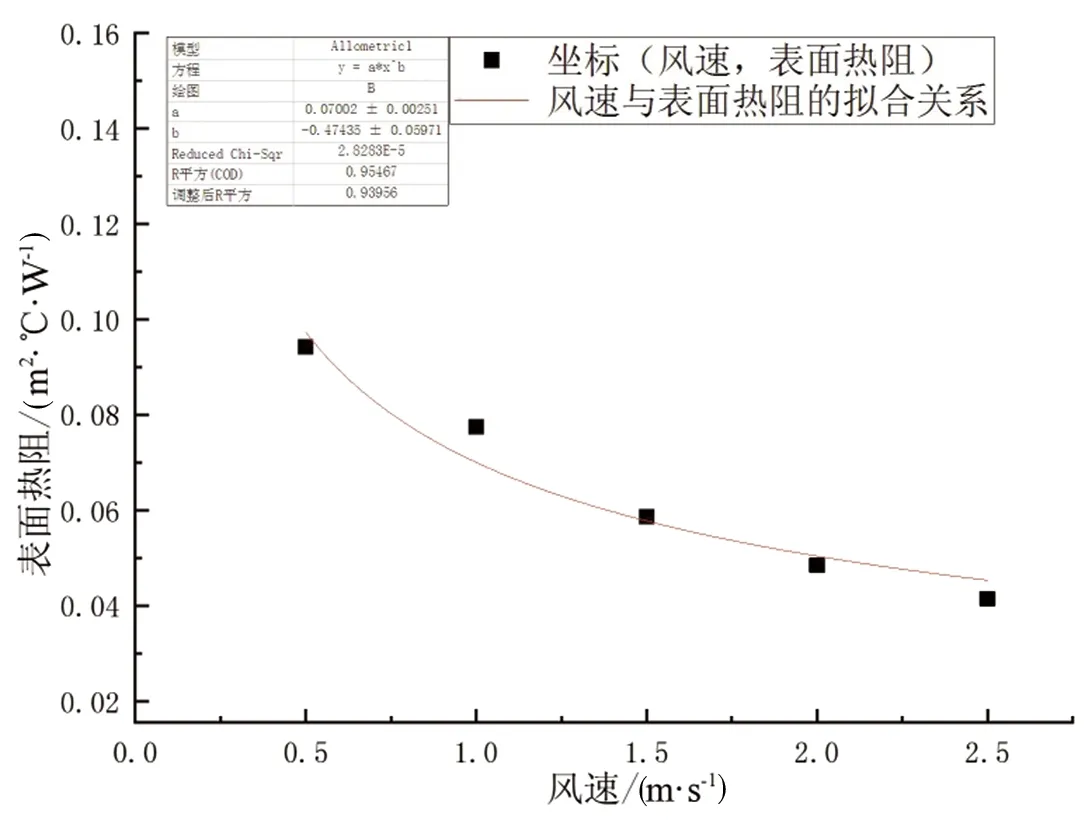
图10 风速与服装表面热阻的关系

表面热阻与风速的关系表达式为

Ia=0.070 02v-0.474 35.

(8)

试验结果显示在环境风速为1.5 m·s-1时,干湿服装的热阻均出现拐点,此时风速为1.5 m·s-1,表面热阻为0.058 m2·℃·W-1,风流开始破坏边界层的难度增加,导致热阻出现拐点.

4 结论

1)相对湿度、风速及服装汗湿量均与服装热阻呈负相关.

2)表面热阻与风速的关系表达式:Ia=0.070 02v-0.474 35.

3)风速为1.5 m·s-1,表面热阻为0.058 m2·℃·W-1,风流开始破坏边界层的难度增加,服装热阻出现拐点.