贵州低透无烟煤分形维数表征及其影响因素

李照平,袁梅,许石青,张锐,杨萌萌,徐林

(贵州大学 矿业学院,贵州 贵阳 550025)

贵州省煤炭资源丰富,且煤炭品质优良,是我国煤炭的重要供应地区.但由于贵州地质构造复杂,许多煤层属于低透高瓦斯含量煤层,制约着贵州的煤炭安全生产.煤是一种多孔介质,内部含有大量孔裂隙,煤层孔裂隙是瓦斯赋存及运移的主要场所,孔裂隙的连通性及复杂程度控制着煤层内瓦斯含量及瓦斯流动的难易程度[1],但由于煤层中孔裂隙具有极强的非均质性,采用传统的几何方法难以精确描述和分析其复杂性[2].

分形反映复杂形体占有空间的有效性,是复杂形体不规则性的量度,储层分形维数是描述储层分形特征的一个重要参数,代表储层表面粗糙度或内部复杂程度[1],已有许多国内外学者通过多种手段对砂岩、页岩及煤等低渗透储层的分形维数做了研究.Zhang等[2]通过扫描电镜、核磁共振(NMR)及CT扫描等试验分析砂岩孔隙结构分形特征及其与NMR参数及渗透率的相关关系;Zhang等[3]以分形理论为基础,建立数学模型，分析了低透储层的孔隙分形维数、迂曲度分形维数、表面润湿性及水黏度对油气运移的影响;杨峰[4-5]、朱汉卿等[6]基于低温氮吸附试验,利用FHH模型计算页岩分形维数以表征其孔隙分形特征;叶桢妮等[7]开展压汞试验及扫描电镜试验,使用Menger模型和计盒维数法计算试验煤样的分形维数;张憧[8]利用扫描电镜和低温氮吸附试验数据计算低透煤层分形维数;姜文等[9]借助压汞试验利用washburn方程计算高变质石煤的分形维数并分析其与孔渗特征的联系;李子文等[10]以低温氮吸附试验数据为基础,使用FHH模型计算煤样分形维数,依托Langmuir方程拟合分析了分形维数对煤层吸附瓦斯的影响;高为等[11]基于压汞试验计算黔西地区煤样的综合分形维数以表征煤整体复杂程度,并分析综合分形特征对煤孔渗特性的影响;贾腾飞等[12]利用低温氮吸附及压汞试验数据,使用4种模型计算煤样分形维数,探讨了多尺度分形特征综合表征的方法,并对分形模型进行优选.

以上研究或仅借助单一试验表征储层某段孔径内孔隙分形特征,或进行全孔径段孔隙分形特征表征，但未研究孔隙分形维数对储层储集物性的具体意义.基于此,笔者以贵州低透无烟煤为研究对象,利用低温氮吸附试验和压汞试验数据,采用分形模型计算不同孔径段分形维数，分析其对储层储集特性的意义;以不同孔径段的孔隙体积占比作为权值对分段分形维数进行加权求和,求取综合分形维数并分析其对瓦斯运移的影响;最后使用灰色关联分析探究对分形维数影响最大的因素及原因,为提高贵州低透无烟煤煤层气产出及瓦斯灾害防治等提供理论依据.

1 样品采集与制备

试验样品采自贵州六盘水、黔北、兴义及织纳矿区的突出煤层,这些煤层具有高瓦斯,低透气,难抽采等特性,将煤样分别编号为L7,Q9,X17,Z8,煤层基本参数见表1.

试验煤样均取自新暴露煤层,取样后立即密封运至实验室,经破碎筛分后挑选试验所需不同粒径的煤样.选择其中粒径小于0.15 mm的200 g左右煤样放至干燥皿,用作工业分析试验;选择粒径在0.20～0.25 mm的煤样20 g,在85 ℃下真空烘干6 h,放入干燥皿,用作低温氮吸附试验;选择2 ～5 g的煤块,在80 ℃下真空烘干6 h,放入干燥皿用作压汞试验.

表1 试验煤层实测参数

2 试验与测定结果

2.1 工业分析试验

煤的工业分析包括水分(M)、灰分(A)、挥发分(V)、和固定碳(Fc)这4个分析项目指标的测定,其中水分、灰分、挥发分直接测定得到,固定碳使用差减法计算.工业分析使用WS-G818全自动工业分析仪进行工业分析测定,测定结果见表2.

表2 工业分析结果 单位：%

2.2 低温液氮吸附试验

低温氮吸附试验采用的是低温液氮物理吸附静态容量法,该方法原理是恒定温度条件时,在特定的吸附压力下,固体表面上吸附定量的气体,通过测定不同压力下对应的气体吸附量,可得到吸附等温线,由此可计算出比表面积与孔径分布.本次低温氮吸附试验采用3H-2000PS1/2型比表面积及孔径分析仪完成,测试范围为0.35～400 nm,试验结果包括煤样孔隙孔径及孔体积、比表面积等见表3.

表3 孔径及孔体积和比表面积测定结果

2.3 压汞试验

压汞试验采用 Auto pore IV9510 压汞仪完成,该仪器的主要功能是测量粉末或块状固体的开放孔和裂隙的孔尺寸和孔体积及其他参数,测量范围在 0.003 5～1 000 um; 工作压力：低压段为3.45～310 kPa，高压段最大压力为413 685 kPa，工作温度为 15～40 ℃；高、低压传感器测量精度≤±0.11%.该仪器原理：样品颗粒间的液态汞被压入孔中时,被汞侵入的孔径是所用压力的函数.压汞试验结果见表4.

表4 压汞测试结果 单位：%

3 分形维数表征及其影响因素分析

3.1 分形维数表征

煤的孔隙结构复杂,其研究方法也较多,使用较广泛的有低温气体吸附法[13-14]、压汞法[2,11]等,有学者通过低温氮吸附试验结合压汞试验对孔隙特征进行联合表征[8,15],将孔隙分为微小孔(吸附扩散孔)、中大孔(渗流孔)和裂隙孔,可据此将煤分形维数分为吸附扩散孔分形维数(Dk)、渗流孔分形维数(Ds)及裂隙孔分形维数(Dl)以表征整体孔隙复杂程度.

本文采用低温氮吸附试验和压汞试验联合表征全孔径范围孔隙结构复杂程度,在霍多特孔隙分类方法的基础上,结合流体注入法测试孔径的特性[16]及瓦斯分子吸附特性[17],参考叶祯妮等[8]的研究,具体孔径划分如下:孔径小于0.1 μm为吸附扩散孔,孔径0.1～5.0 μm为渗流孔,孔径大于5.0 μm为裂隙孔.利用低温氮吸附试验,使用FHH模型计算吸附扩散孔分形维数:

lnVq=A+Kln[ln(Po/Pq)].

(1)

式中:Vq为在平衡压力Pq下的气体吸附量;Po为气体的饱和蒸汽压;Pq为气体吸附的平衡压力;K为拟合直线的斜率,与吸附扩散孔分形维数Dk呈线性关系;A为常数.

作lnVq-ln[ln(Po/Pq)]曲线并进行线性拟合,拟合度最高的直线斜率为K,根据Dk=K+3计算出分形维数.

对大范围孔径的孔隙复杂程度表征能力最好的是Sierpinski 综合模型[12],故采用Sierpinski 综合模型,基于压汞试验中煤样进汞体积与进汞压力的关系得到式(2)，并利用式(2)计算渗流孔分形维数和裂隙孔分形维数:

lnVg=lnα+(3-D)ln(Pg-Pt).

(2)

式中:Vg为进汞量,mL/g;α为常数,无量纲;Pg为进汞压力,Pt为门限压力,MPa;D为煤渗流孔分形维数Ds或裂隙孔分形维数Dl,无量纲.

根据压汞试验数据作lnVg-ln(Pg-Pt)散点图进行线性拟合得到斜率K,即可求得分形维数D=3-K.

渗流孔分形维数(Ds)、裂隙孔分形维数(Dl)能分别表征渗流孔及裂隙孔的复杂程度,但难以代表煤样整体孔隙复杂程度,高为等[11]使用魏建平等[18]提出的一种煤样综合分形维数计算方法,即以不同孔径段孔体积占比作为权值,对相应孔径段分形维数进行加权求取综合分形维数,公式如式(3).

Dc=VsDs+VlDl.

(3)

式中:Dc为综和分形维数;Ds为渗流孔分形维数;Dl为裂隙孔分形维数;Vs为渗流孔体积占总孔体积比;Vl为裂隙体积占总孔体积比.

现有煤层孔隙裂隙研究将煤中发育的孔隙分为4类[19]如表5所示,据此分类,文中裂隙孔及少部分较大渗流孔主要为粒间孔,较小渗流孔主要为粒内孔.

表5 孔隙分类

综上,计算煤样吸附扩散孔分形维数、渗流孔分形维数、裂隙孔分形维数及综合分形维数，结果见表6.

表6 分形维数计算结果

迂曲度指流体在多孔介质中渗流时,流体质点所走过的距离与孔隙介质外形几何长度之比,反映孔隙介质内部连通孔隙弯曲程度,迂曲度越大,流体在孔隙通道中流动受到的阻力越大,因此迂曲度在一定程度上能表征煤样孔隙的复杂特征及储层渗透能力[20].煤层中瓦斯渗流主要场所为渗流孔和裂隙孔,有研究表明,综合分形维数越大,煤层渗透率越低[11].试验煤样综合分形维数与迂曲度间的拟合关系如图1所示.

根据图1可知,4个煤层煤样迂曲度与综合分形维数呈正相关关系,这是因为煤样迂曲度增大,内部连通孔隙弯曲程度增大,使得孔隙结构变复杂.结合表1,随着煤综合分形维数增大,煤层透气性系数减小,煤样X17综合分形维数最大,为2.806 0,其煤层透气性系数仅为0.009 m2/(MPa2·d);煤样Q9综合分形维数最小,为2.651 6,其透气性系数在0.05～7.17 m2/(MPa2·d).由此可见,综合分形维数能更好表征贵州矿区低透无烟煤孔隙复杂程度,且其综合分形维数越大,煤迂曲度越大,透气性越差.

煤层原始瓦斯含量是指未受开采和抽放影响的煤体内单位质量或单位体积瓦斯含量,煤层原始瓦斯含量由煤田地质条件、煤变质程度、煤岩结构及组分等因素决定[21],而煤吸附瓦斯的主要场所为微小孔[19],因此煤层原始瓦斯含量在一定程度上反映煤中微小孔孔隙结构复杂程度与瓦斯吸附能力.试验煤样吸附扩散孔分形维数与原始瓦斯含量之间的拟合关系见图2.

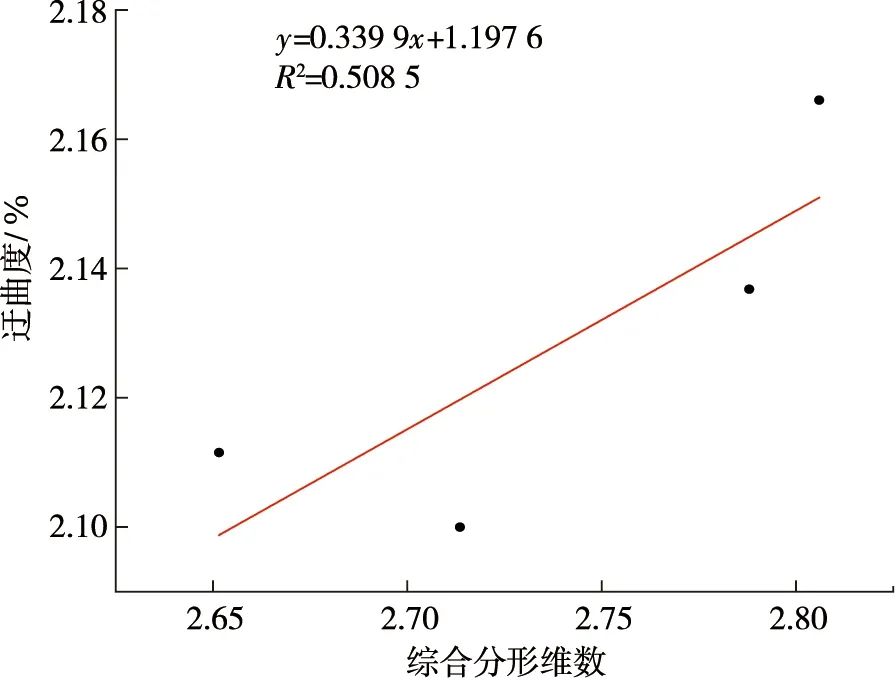
图1 综合分形维数与迂曲度关系

图2 吸附扩散分形维数与原始瓦斯含量关系

由图2可知,吸附扩散孔分形维数与煤中原始瓦斯含量呈正相关关系,说明贵州矿区低透无烟煤吸附扩散分形维数越大,微小孔孔隙结构越复杂,煤吸附瓦斯的能力越强.

3.2 基于灰色关联分析的分形维数影响因素研究

灰色关联分析是灰色系统理论中一个重要的研究领域,主要根据序列曲线的几何形状来判断两序列之间的相近关系或相似性,通常采取线性插值法将观测系统离散行为的观测数据转换为分段连续线,然后根据线条的几何特征构建相应的模型以判断序列之间的相似性,包括距离、面积、斜率等特征,越为相似的观测对象,其几何特征也越相近[22-23].灰色关联度分析作为衡量因素间关联程度的一种方法,不受样本量及样本分布规律的影响,在应用时不会出现量化结果与定性分析结果不符的情况.

灰色关联分析主要有确定参考序列和比较序列、序列无量纲处理、计算关联系数、求关联度及关联度排序几个步骤,在本文中的应用如下:

1)确定参考序列和比较序列

反映系统行为特征的数据序列,称为参考数列;影响系统行为的因素组成的数据序列,称为比较数列[23].故选择煤样吸附扩散孔分形维数Dk作为参考序列,平均孔径、总孔体积、总孔比表面积作为比较序列;选择综合分形维数Dc作为参考序列,选择灰分、挥发分、固定碳含量作为比较序列,煤样原始数据如表7所示.

表7 煤样原始数据

2)参考序列、比较序列无量纲化

由于各因素数据的单位、数量级不同,代表的意义不同,为便于比较,进行数据的无量纲化处理.采取初值法进行数据的无量纲化,即对每一组数据均用该组的第一个数据去除,得到一列新的数据列.

3)关联系数计算

(4)

式中:εi为第i个因素的关联系数;minmin|x0i-xii|为两级最小差;maxmax|x0i-xii|为两级最大差;ρ为分辨系数,此处取0.5;Δxi为差序列.

4)关联度计算

(5)

式中:ri为第i个影响因素的关联度;n为影响因素的个数.

经过上述步骤,计算出的关联度如表8和表9所示.由表8可知固定碳与综合分形维数关联度最高,说明固定碳含量对综合分形维数影响最大,究其原因是煤样中固定碳含量最高,当固定碳质量分数为 75%～87%时,随着质量分数的增加,煤的孔隙将会减小；而当煤的固定碳质量分数在87.0%～93.4%时,由于煤大分子的芳环叠片聚集成 5～10 nm 的芳环束,叠片的层间距减小,其间的偏斜方位降为15°,煤大分子的排列规整,从而导致煤中孔隙增大[24],进而影响煤中孔隙结构的复杂程度.相对固定碳含量而言,与综合分形维数关联度较低的是灰分,这是因为灰分主要是由碳酸盐、硅酸盐等盐类次生灰分和原生灰分组成[25],而盐类矿物主要发育孔径较小的溶蚀孔,对表征渗流孔和裂隙孔的综合分形维数影响较小.

表8 综合分形维数影响因素灰色关联度

当灰色关联度大于0.9时,表明比较序列的因素对参考序列的变量有十分显著的影响；当关联度在[0.8,0.9]时,该因素影响相对显著；在[0.7,0.8]时,比较序列的因素对参考序列的变量的影响比较大；当灰色关联度小于0.6时,该影响因素可以忽略不计[26]。由表9可知3种影响因素中，对吸附扩散孔分形维数影响最大的是平均孔径,影响最小的是总孔比表面积.这是因为瓦斯吸附扩散孔主要由微孔小孔提供,而根据FHH方程可知,气体吸附量、压力决定分形维数,微孔作为气体吸附的主要场所[14],其孔隙比表面积越大,气体吸附能力越强,所以对分形维数影响最大;但根据表4,X17煤样比表面积很大说明微孔最多,符合这一规律,但该试验其余3个煤样微孔含量远少于小孔含量,贡献较少的比表面积,故对分形维数影响相对较小.总孔比表面积与吸附扩散孔分形维数呈正相关关系[10],虽然与分形维数关联度不如平均孔径大,但关联度大于0.7的总孔比表面积也对分形维数产生较大的影响.

表9 吸附扩散孔分形维数影响因素灰色关联度

4 结论

1)吸附扩散孔分形维数可表征贵州低透无烟煤中微、小孔的孔隙复杂程度,也能反映无烟煤吸附瓦斯的能力,吸附扩散孔分形维数越大,无烟煤吸附瓦斯的能力越强.

2)综合分形维数能更准确地表征贵州低透无烟煤的整体孔隙复杂程度,并在一定程度上反映其透气性,综合分形维数越大,透气性越差.

3)通过灰色关联分析计算发现,对试验煤层渗流扩散孔分形维数影响最大的为平均孔径,总孔比表面积对其影响最小;固定碳含量对试验煤层综合分形维数影响最大,挥发分对其影响最小.