新月形内齿轮泵内部泄漏与黏性摩擦损失模型构建

柴红强，杨国来，刘小雄，刘秉昊，史有程

新月形内齿轮泵内部泄漏与黏性摩擦损失模型构建

柴红强1，杨国来1※，刘小雄2，刘秉昊3，史有程1

（1. 兰州理工大学能源与动力工程学院，兰州 730050；2. 乐卓液压科技有限公司，苏州 215000；3. 兰州交通大学招标中心，兰州 730070）

为了准确表征新月形内齿轮泵的内部流动特性，该研究根据静压支撑油膜理论及牛顿摩擦定理构建了该型齿轮泵内部泄漏数学模型及黏性摩擦损失数学模型，依据齿轮泵结构特点以及实际流动特征建立了基于两相流及动网格技术的CFD仿真模型，模拟分析了齿轮泵内部含气油液的流动特性，并与理论计算结果进行对比，最后进行试验验证。结果表明：在1/3周期内的瞬时体积流量与瞬时输入功率曲线均呈现连续周期性变化，2条曲线都有4个脉动；由于理论分析无法全面考虑油液实际流动过程而导致总泄漏量的理论值与仿真值相差60.11%，总黏性摩擦功率损失的理论值与仿真值相差66.67%；静态区域中流线相互平行，质点流动呈现层流状态，而在运动区域中却呈现完全湍流形态；压差流沿着新月形隔板内外两侧壁面以超过12 m/s的速度逆时针运动，而剪切流沿着外齿轮及内齿圈外壁同样以超过12 m/s的速度顺时针运动，在完全密封的齿间出现不同尺度的旋涡，旋涡中心的液体脱落现象使得其中的流体速度为0。在啮合齿面油膜的密封作用下，间隙最小处出现断流，啮合区的最大泄漏量为0.16 L/min；试验与仿真的容积效率相差1.33个百分点，偏差率为1.36%；试验与仿真总效率相差1.39个百分点，偏差率为1.73%。该研究获得了新月形内齿轮泵流动特性精确数学模型，验证了数值计算模型的适用性及仿真结果的准确性，可为完善齿轮泵设计理论与内流场特征分析提供参考。

齿轮泵；试验；内部泄漏；黏性摩擦损失；动网格；多相流

0 引 言

新月形内齿轮泵是现代农业装备液压系统中的能量转换装置，其运动部件由具有直线齿廓的外齿轮及具有高阶圆弧齿廓的内齿圈组成[1-2]，广泛应用于耕作、播种以及灌溉等农业机械。

油液压传动以油液为工作介质进行能量和信号传递，油液相当于整个系统的血液，将系统中的各类元件联系起来形成一个有机整体。油液中不可避免地掺混一定的游离气体，形成含气油液。油液含气对其基本属性，特别是等效体积弹性模量产生非常大的影响[3-7]。

新月形内齿轮泵中无轴向及径向间隙自动补偿结构，摩擦副之间依靠固定的微小间隙实现密封、润滑及传递作用力。齿轮副作为齿轮泵的唯一运动部件，齿廓曲线影响着其流动特性。黄溧震[8]最早根据齿廓啮合基本定理使用齿廓法线法推导了外齿轮及内齿圈的齿廓方程，并给出了解析式的取值范围，最后通过实例验证了表达式的正确性。在此基础上，Sung等[9-13]不断优化设计方法从不同角度求解了共轭齿廓的数学模型并确定了齿轮副参数的取值范围。

输出流量脉动是容积式液压泵的固有属性，这种有害现象是无法完全消除的。流量脉动与回路阻抗共同引起的压力脉动不仅损坏系统内薄弱零部件，还会引起元件振动，同时产生流体噪声。崔建昆等[14]最早基于齿轮啮合原理求解了瞬时流量及流量脉动率近似方程。此后研究中，段刚等[15-17]简化了近似方程并分析了轮齿参数对流量近似方程的影响。然而，近似方程对于精度要求较高的场合并不适用。因此，Chai等[18]鉴于容积变换法及数形结合法详细推理了精确流量方程，确定了设计变量取值范围并获得了齿轮副参数对流量的影响规律，最后利用数值计算与试验论证相结合检验了相关解析式的准确性。

表征新月形内齿轮泵的内部流动特性的指标还包括内部泄漏及黏性摩擦损失等，但目前还没有相关研究报道。本文基于油膜设计理论构建内部泄漏数学模型及功率损失数学模型，同时结合动网格技术及两相流模型特征提出一种用于新月形内齿轮泵数值计算的分布式参数模型，在考虑摩擦副间油膜厚度的基础上建立内流道仿真模型并进行数值计算，最后进行相关试验对仿真结果进行验证。

1 数学模型建立

1.1 含气油液动态模型

影响油液动态特性的主要因素包括密度、动力黏度以及等效体积弹性模量等。含气油液中一般存在3种成分，分别为纯流体、游离气体及油蒸气，混合相密度方程为

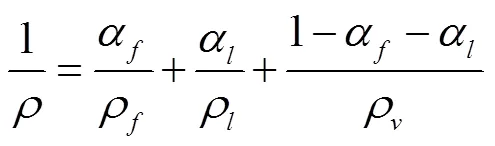
气相成分的密度可根据理想气体状态方程获得：

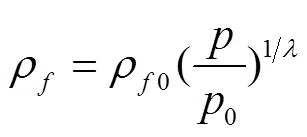
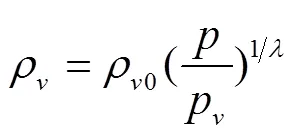
含气油液绝对黏度方程为

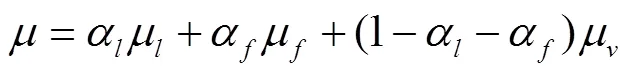
含气油液等效体积弹性模量方程为

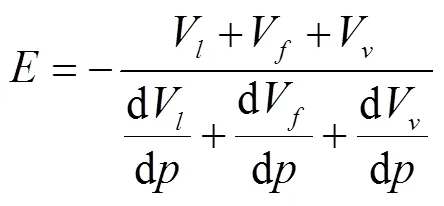
式中为含气油液等效体积弹性模量，MPa；V、V及V分别为纯流体、游离气体及油蒸气的初始容积，L；dV/d分别为对应的变化率，L/MPa。

根据导数定义对式（5）进行变换可得：

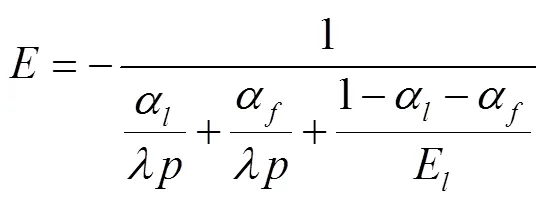
式中E为纯流体等效体积弹性模量，MPa。

1.2 新月形内齿轮泵内部泄漏数学模型

新月形内齿轮泵中的泄漏部位包括轴向间隙、径向间隙及啮合齿面。在正常啮合情况下，通过齿面接触处的泄漏可忽略。首先根据齿轮泵结构建立齿轮泵内部泄漏间隙的三维模型，见图1。

根据图1可知，轴向泄漏间隙包括上下2个端面间隙。径向泄漏间隙包括以轮齿中心为轴线的内外环间隙以及齿轮齿顶与新月形隔板间的间隙。

1.2.1 轴向间隙泄漏量

根据图1，轴向泄漏间隙可由两平行圆盘间隙流动理论计算[19-22]。鉴于间隙很小（通常为几十微米），可忽略由于端面运动造成间隙中油液流动状态的变化。为了便于计算泄漏量，根据压力分布将轮齿端面划分为3个部分，分别为同低压腔接触的区段，同高压腔接触的区段以及高低压腔之间的过渡区段，见图2。

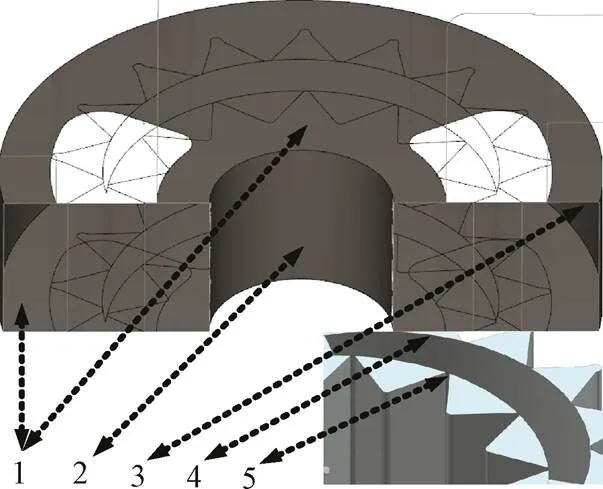
1.轴向间隙 2.外齿轮内壁与轴颈间隙 3.内齿圈外壁与壳体内壁间隙 4.内齿圈齿顶与隔板间隙 5.外齿轮齿顶与隔板间隙

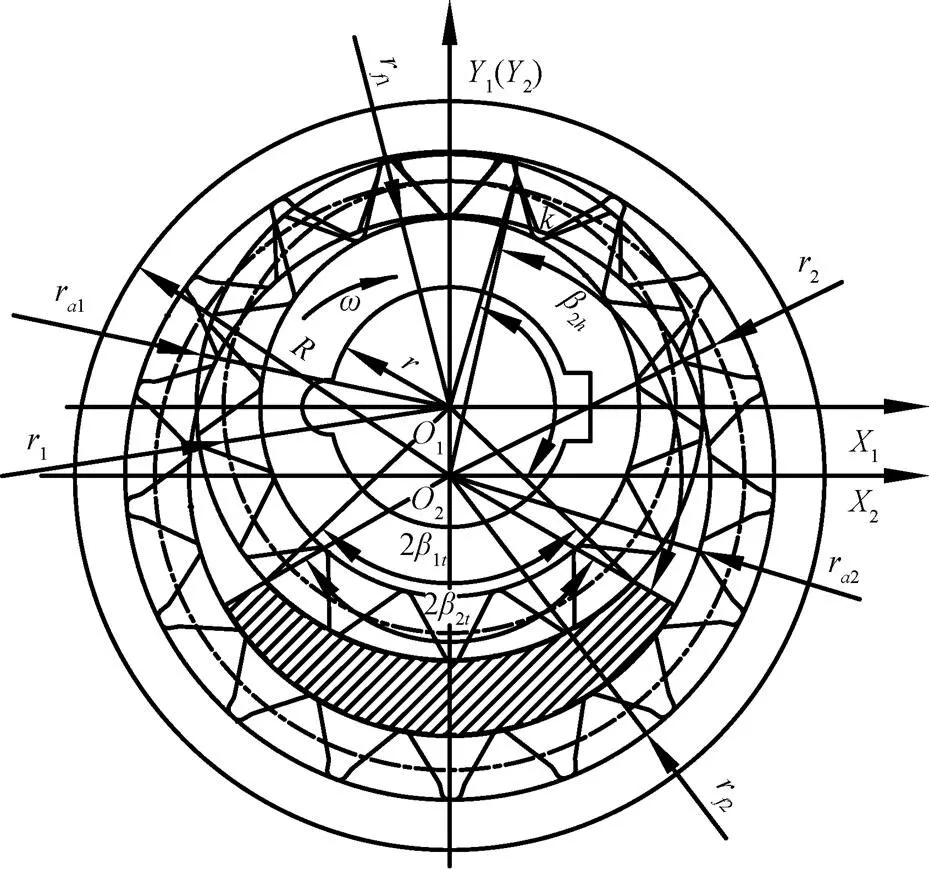
注：β1h外齿轮高压腔包角，(°)；β2h为内齿圈高压腔包角，(°)；β1t为外齿轮过渡腔包角，(°)；β1t内齿圈过渡腔包角，(°)；rf1为外齿轮齿根圆半径，mm；rf2为内齿圈齿根圆半径，mm；ra1为外齿轮齿顶圆半径，mm；ra2为内齿圈齿顶圆半径，mm；r1为外齿轮分度圆半径，mm；r2为内齿圈分度圆半径，mm；r为外齿轮内壁半径，mm；R为内齿圈外壁半径，mm；ω为外齿轮角速度，rad·s-1；O1为外齿轮中心，O2为内齿圈中心，k为啮合点；X1与X2分别为外齿轮与内齿圈的横坐标，Y1与Y2分别为外齿轮与内齿圈的纵坐标。

根据图2几何关系可得齿轮端面间隙中的总泄漏量Δ1为

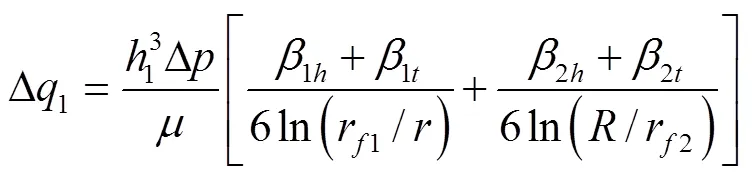
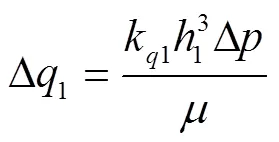
式中1为端面油膜厚度，mm；Δ为高低压腔之间的压差，MPa；为动力黏度，Pa·s。

1.2.2 径向间隙泄漏量

1）齿顶与新月形隔板间泄漏量

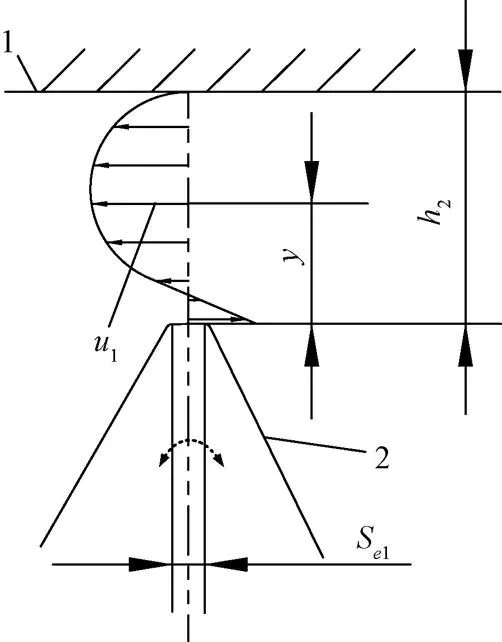
1.新月形隔板 2.外齿轮

1.Crescent spacer 2.External gear

注：为齿顶到新月形隔板间的任一高度，mm；2为外齿轮齿顶油膜厚度，mm；S1为外齿轮齿顶厚度，mm；1为叠加速度，m·s-1。

Note:is the height between the top of the tooth and the crescent spacer, mm;2is the thickness of the oil film on the top of the outer gear tooth, mm;S1is the thickness of the top of the outer gear tooth, mm;1is the stacking velocity, m·s-1.

图3 外齿轮齿顶与新月形隔板间速度分布示意图

Fig.3 Diagram of speed distribution between teeth top of the external gear and crescent spacer

在图3中，外齿轮齿顶与新月形隔板间的叠加速度1可表示为

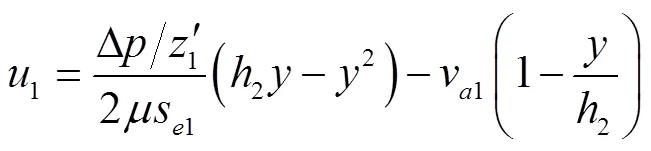
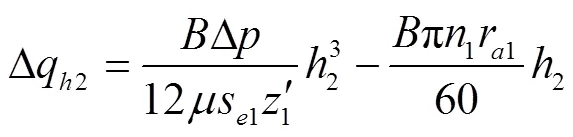
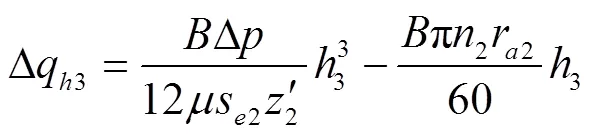
2）外齿轮内壁与轴颈间泄漏量

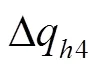
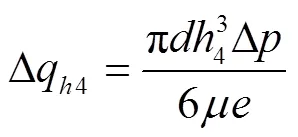
式中4为外齿轮内壁油膜厚度，mm；为外齿轮内壁深度，mm；为外齿轮内壁直径，mm。

3）内齿圈外壁与壳体内壁间泄漏量

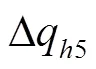
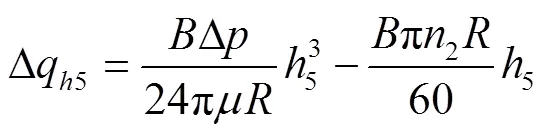
式中5内齿圈外壁油膜厚度，mm。

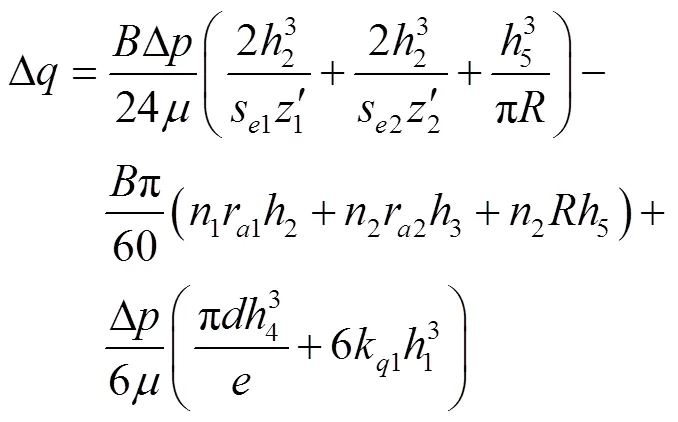
由式（14）可知，高低压腔的压差越大，黏度越小，泄漏量越高；外齿轮转速越大，泄漏量越小。

1.3 新月形内齿轮泵黏性摩擦损失数学模型

1.3.1 轴向间隙黏性摩擦损失

外齿轮端面简化图，见图4。

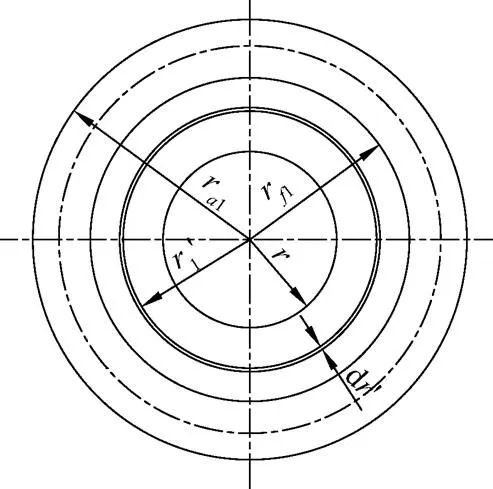
注：为外齿轮内壁到外齿轮齿根圆之间的任意半径，mm；drʹ为半径处微元环宽度，mm。

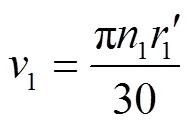
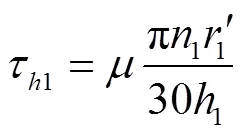
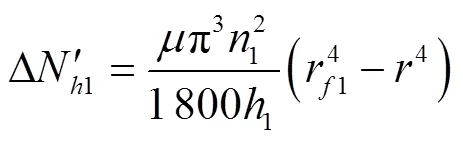
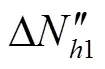
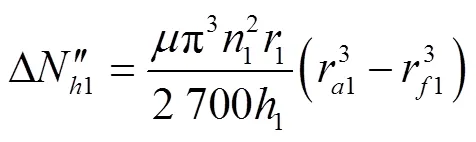
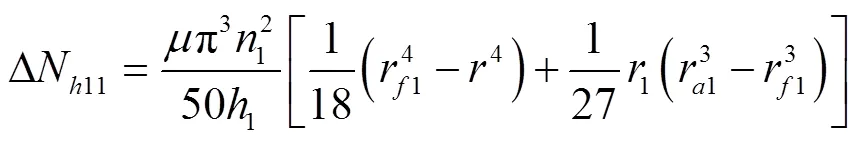
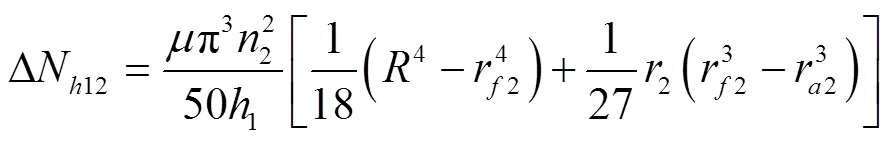
1.3.2 径向间隙黏性摩擦损失

由于外齿轮内壁与轴颈间无相对运动，因此只需计算外齿轮齿顶、内齿圈齿顶分别与新月形隔板间的黏性摩擦损失及内齿圈外壁与壳体间的黏性摩擦损失。

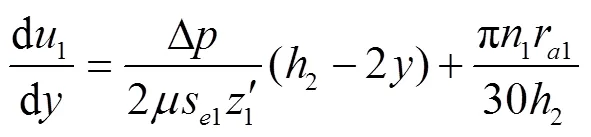
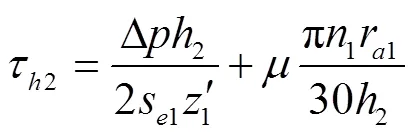
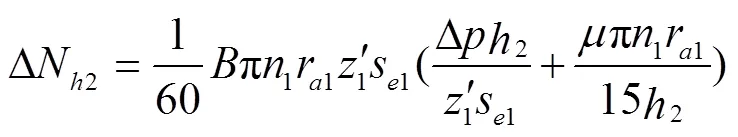
同理可得内齿圈齿顶以及内齿圈外壁黏性摩擦损失ΔN3与ΔN5分别为

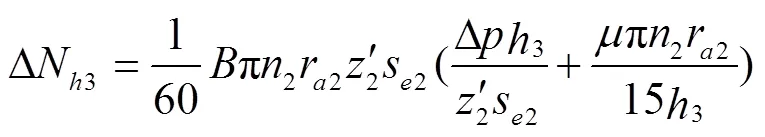
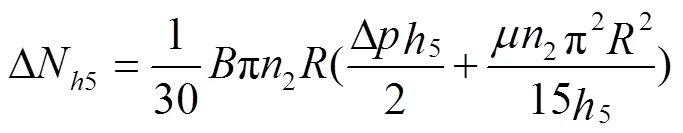
综上可得新月形内齿轮泵的总黏性摩擦损失Δ为

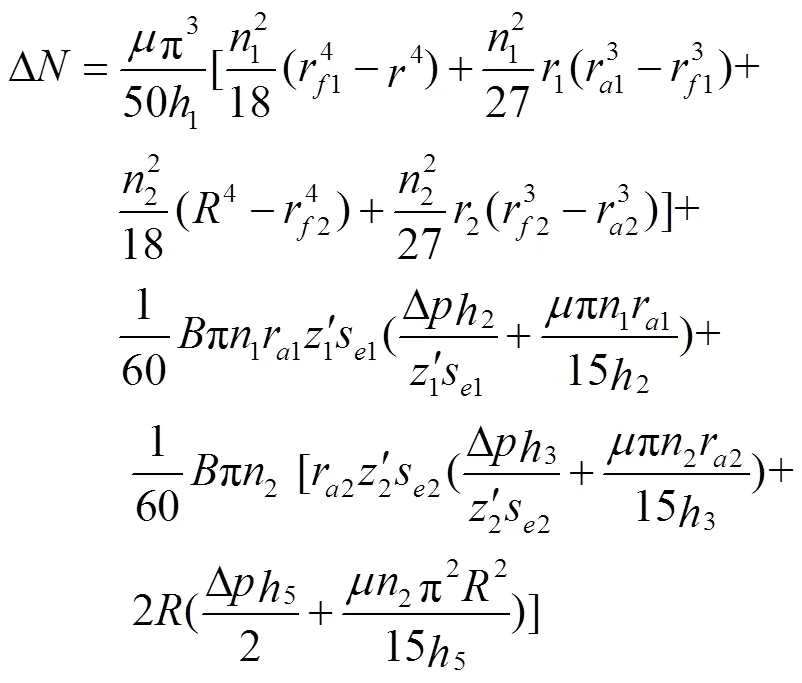
由式（26）可知，外齿轮转速越高，黏度越大，高低压腔压差越大，黏性摩擦损失越大。

2 新月形内齿轮泵CFD仿真模型

为进一步验证所建数学模型的准确性，对给定新月形内齿轮泵进行数值计算。

2.1 三维内油道网格模型

CFD仿真模型本质上属于分布式参数模型，在迭代过程中需要把连续的初始空间域离散化，进一步求解离散点上的代数方程组从而获得物理场的近似值。因此，本文首先获取考虑内泄漏的初始油道三维模型，见图5。

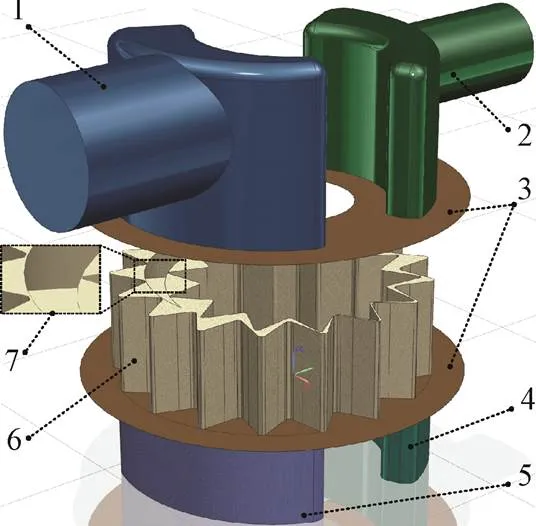
1.出口油道 2.进口油道 3.轴向油膜 4.进口配油道 5.出口配油道 6.转子油道 7.径向油膜

需要说明的是，综合考虑加工工艺、油液过滤精度等因素，确定初始油道模型中的泄漏间隙，其中轴向与径向泄漏间隙均为0.12 mm，初始啮合齿面间的最小间隙为0.03 mm。

图5中对应齿轮副参数见表1。

根据内油道结构特征，本文采用混合网格对三维初始油道模型进行离散化，其中转子油道为非结构化网格，最低网格质量为0.71；其余油道为结构化网格，最低网格质量为0.35，三维内流道网格模型见图6。

2.2 仿真参数设置

2.2.1 边界条件及运动壁面程序

齿轮泵初始内油道网格模型中有壁面边界、流动进口边界以及流动出口边界，其中外齿轮及内齿圈对应壁面都为周期性旋转的运动壁面，需要编写C语言程序模拟其运动规律（即在程序中给定外齿轮转速为2 000 r/min，根据传动比计算内齿圈转速为1 529.4 r/min，运动周期为0.03 s），其余均为静止壁面；流动进口边界为压力进口（压力值为0.1 MPa），流动出口边界为压力出口（压力值为7.5 MPa）。

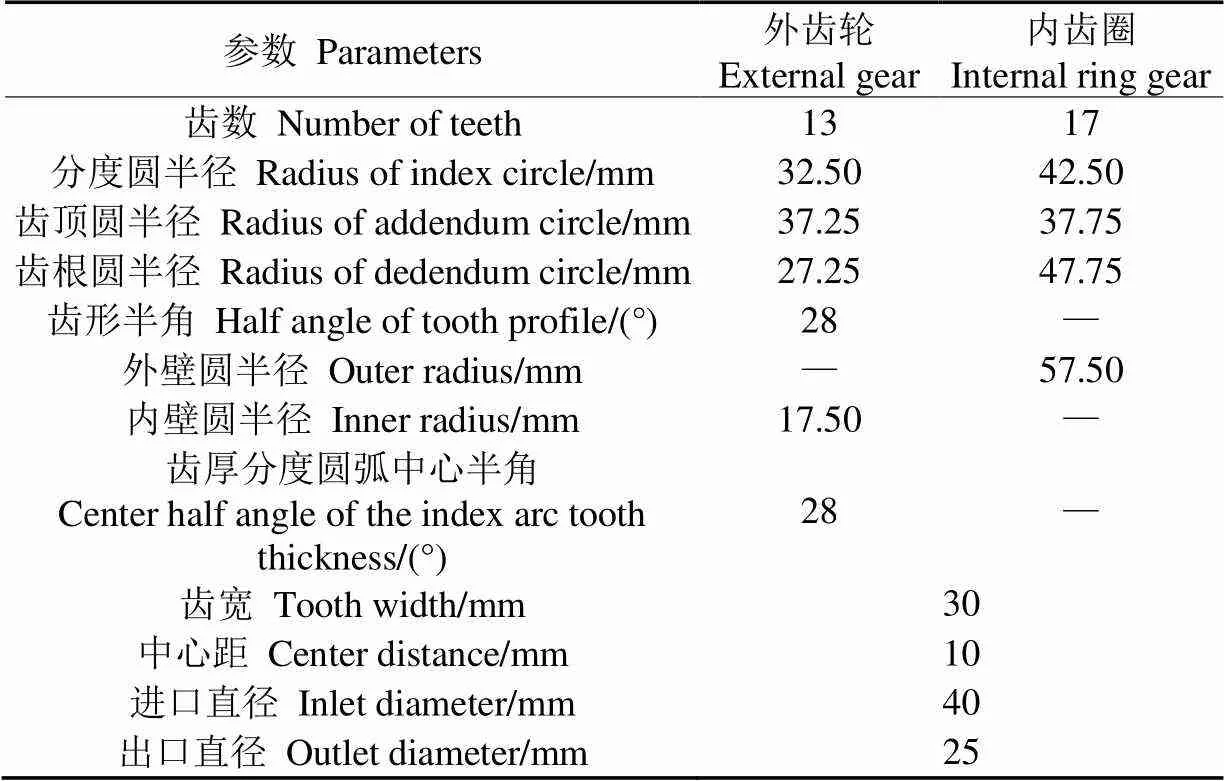
表1 齿轮副参数

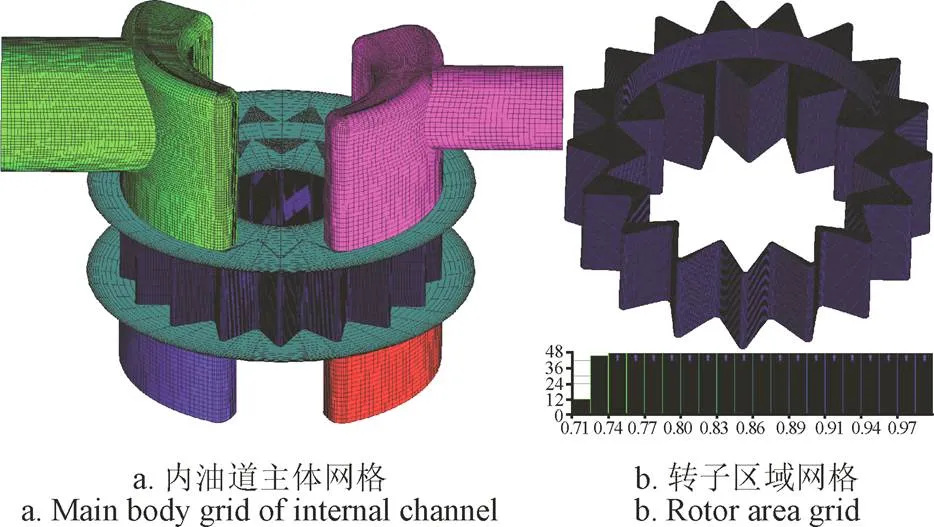
图6 初始内油道三维网格模型

2.2.2 流动介质

齿轮泵工作参数为排量22.8 mL/r，最大转速3 000 r/min，出口压力额定值7.5 MPa、峰值12.5 MPa，矿物油黏度范围10～100 mm2/s。基于此，本文采用46#抗磨液压油作为工作介质，其基本属性为含气量0.1%，油温40 ℃，密度852.98 kg/m3，动力黏度0.043 Pa·s，等效体积弹性模量1 685.91 MPa。

2.2.3 两相流模型

油液中不可避免地掺混一定体积分数的空气，为了准确描述含气油液的流动过程，本文采用两相流模型中的Mixture模型。为了表征纯油液与游移气体之间的相互作用，需要求解Slip Velocity方程。在计算过程中以空气为主相并设定气泡直径为0.01 mm，这样有利于计算稳定性。最后设定时间步长为0.000 01 s，每个时间步内的最大迭代次数为200。

2.2.4 湍流模型

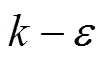
3 计算结果与分析

3.1 网格无关性验证

为了尽可能降低网格数量对计算结果的影响，本文设计了5组网格，对比出口边界的平均流量，同时以节点数最多的数值为基准计算偏差率，具体结果见表2。

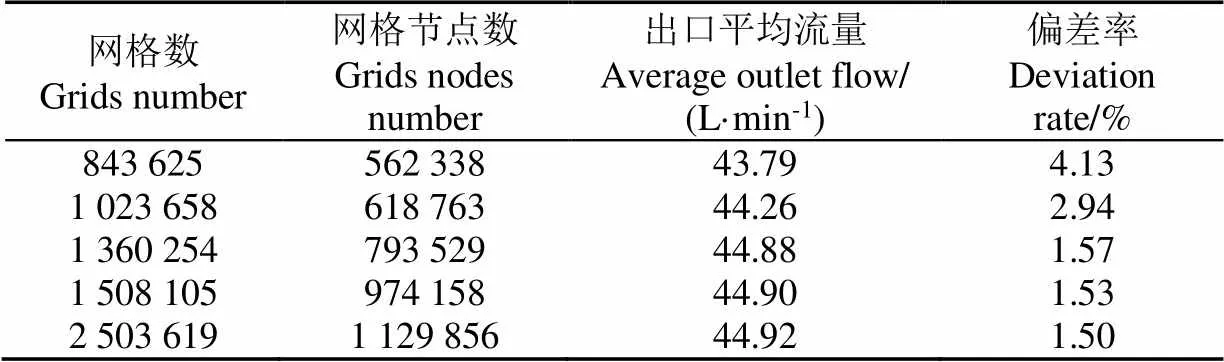
表2 不同网格节点数对应的出口平均流量

由表2可知，不同网格节点数对应计算结果相差较小，为了提高计算效率，本文选择节点数为793 529，网格数为1 360 254的网格模型。

3.2 新月形内齿轮泵流动特性分析

3.2.1 出口瞬时流量

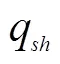
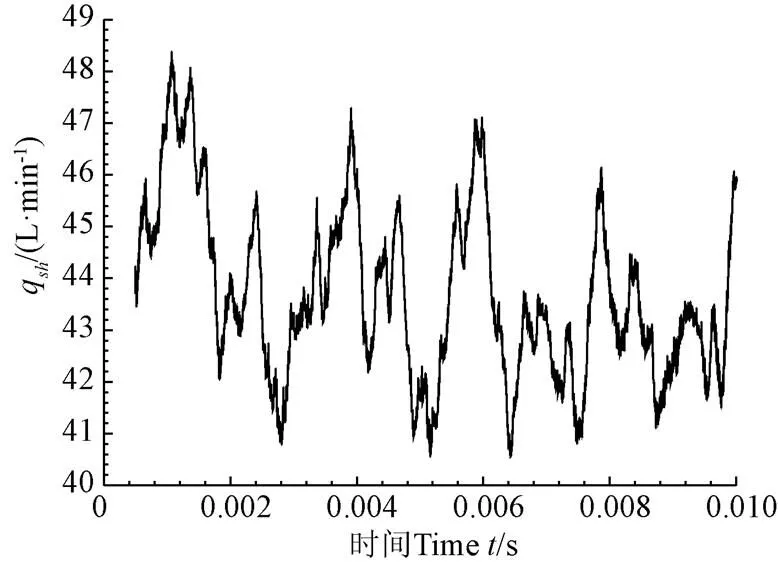
图7 齿轮泵出口瞬时体积流量qsh

与理论瞬时流量不同，仿真流量的瞬时值在不同啮合周期并非完全相同，流量曲线随啮合次数（即齿轮副进入啮合到退出啮合的循环次数）呈现周期性变化，在0.010 s的时间内出现4个脉动。

进一步获取图7的平均流量，根据式（14）及相关定义计算理论泄漏量及容积效率，并将仿真值与理论值进行对比，结果见表3。

由表3可知，理论泄漏量明显低于仿真值，两者相差1.13 L/min，偏差率为60.11%。造成偏差率较大的原因是：流动过程中过流面积发生突变，流束急剧收缩，油液速度迅速变化，流线经历多次转折，流场中出现各种尺度的旋涡，流体之间、流体与零件之间发生碰撞与摩擦，油液具有压缩性等。实际工况的复杂性显然是理论分析无法全面考虑的。因此，根据理论值与仿真值的比值，以数值计算结果为基准，对总泄漏流量数学模型式（14）进行修正，修正系数为2.5，可得修正后的总泄漏量Δ为

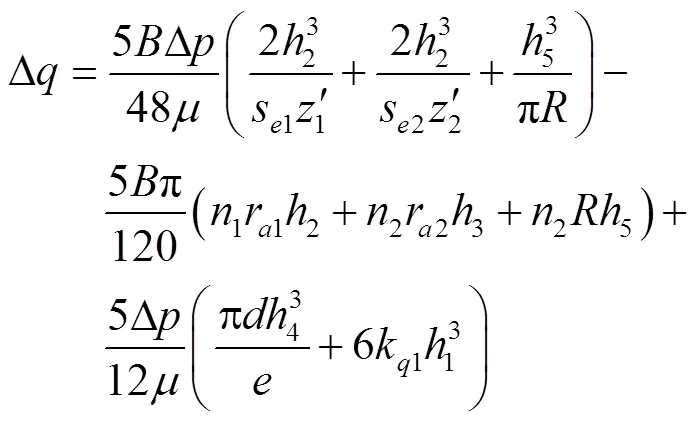
表3 泄漏量及容积效率的理论计算与仿真结果对比

3.2.2 瞬时输入功率

获取1/3周期内的瞬时输入功率N，见图8。

与瞬时流量曲线的变化一致，瞬时功率曲线同样有4个变化周期，与啮合次数相同。

进一步获取图8的平均功率，同时计算功率损失及总效率，并将仿真值与理论值进行对比，结果见表4。

由表4可知，理论损失功率为0.45 kW，远低于仿真功率损失1.35 kW，偏差率为66.67%。其原因为齿轮泵内部功率损失主要包括泄漏损失，油液压缩损失，黏性摩擦损失，机械零件碰撞损失，流体质点摩擦、碰撞损失以及旋涡流能量耗散损失等。然而，理论计算仅为泄漏损失与黏性摩擦损失之和，故较小。因此，根据理论值与仿真值的比值，以仿真结果为基准，对总黏性摩擦损失数学模型式（26）进行修正，修正系数为3，得到修正后的总黏性损失功率Δ为

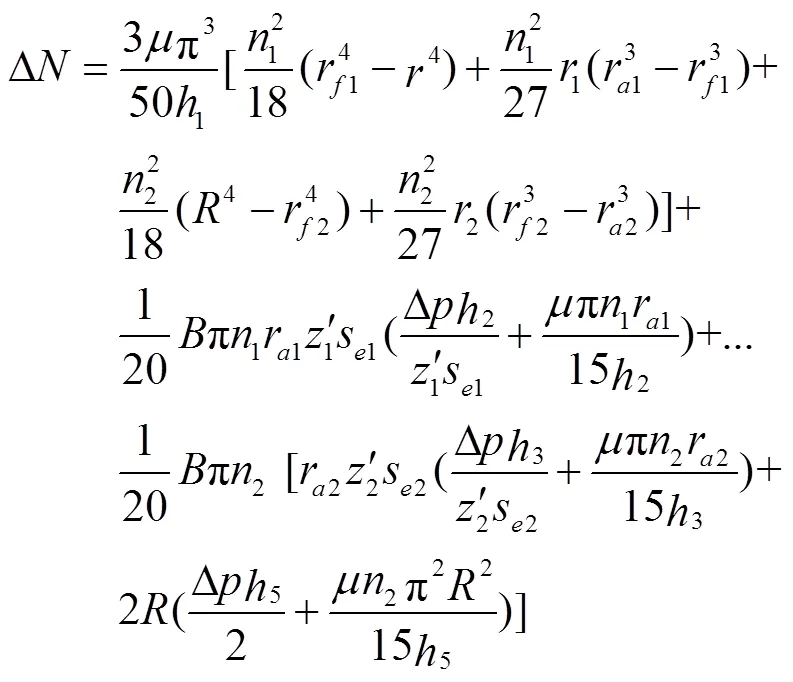
3.2.3 内部流场特性

齿轮泵工作过程中，不同时刻含气油液速度场演变规律相似，本文以齿轮副运动至0.008 8 s，即轮齿退出啮合时的速度场为例进行内部流场特性分析，具体见图9。

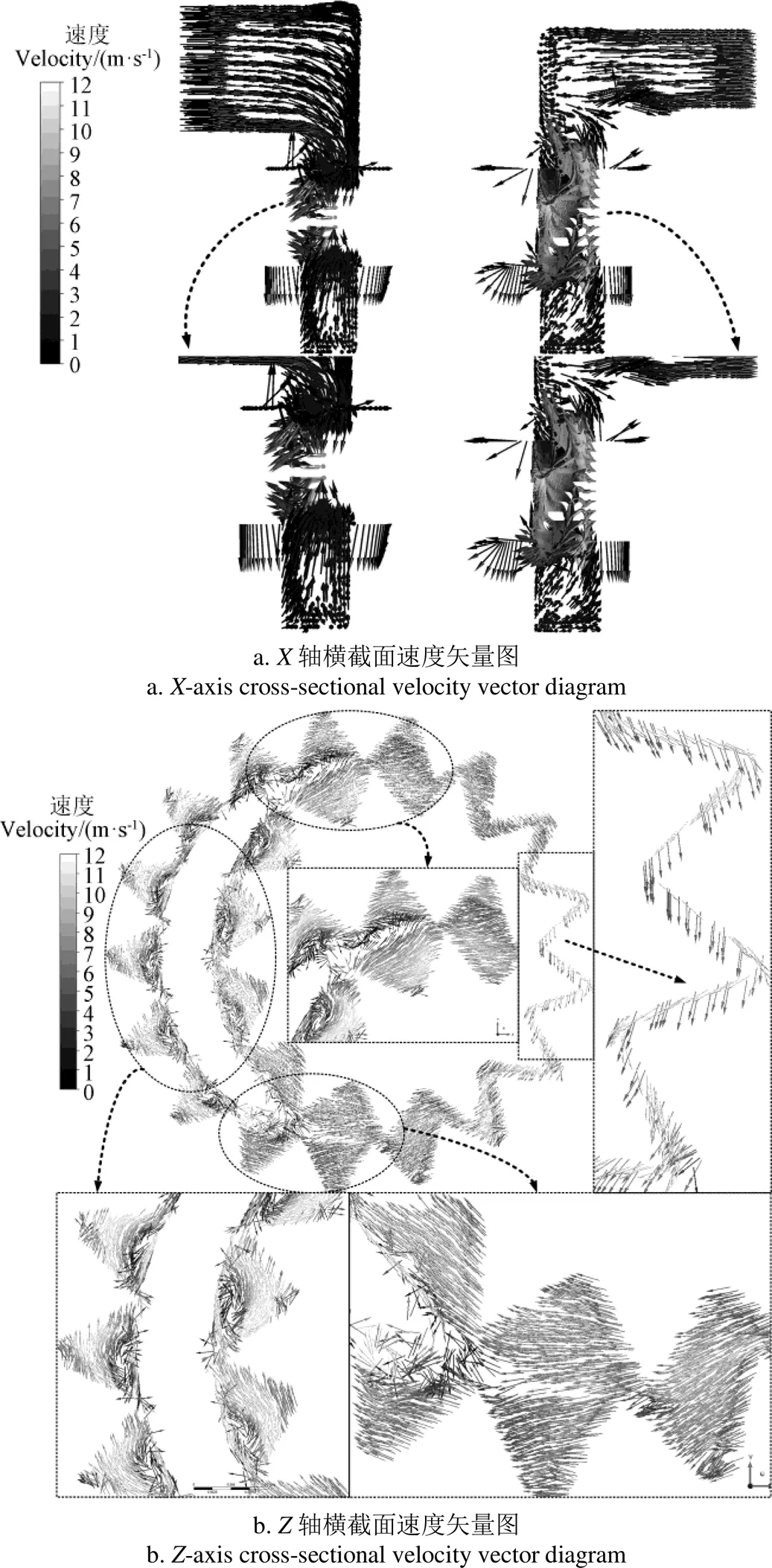
图9 内流道横截面速度矢量图

由图9可知，在压差作用下，进口端面油液经进油通道以1 m/s的流速进入转子区，之后在齿轮副的啮合传动下以2 m/s的速度流入出油通道，最后经出口端面流出。在整个流动过程中，进口油道与出口油道，包括与其对应的配油道中油液分层现象明显。然而，在转子油道与静止油道的交界处以及转子油道中，油液流动方向紊乱，速度梯度变化剧烈，其中流动呈现完全湍流状态。另外，轴向油膜由于泄漏间隙小，密封面积大，其中最高速率超过12 m/s，最低速度小于3 m/s。油液运动呈现层流状态，这与理论假设完全一致。

由于过流面积的突变，流束的急剧变化，使得径向油膜中流体质点运动呈现湍流状态。在完全参与密封的齿间，存在着沿新月形隔板内外两侧壁面以逆时针方向高速（超过12 m/s）运动的压差流与沿外齿轮及内齿圈外壁面以顺时针方向高速（超过12 m/s）运动的剪切流。这样，在环形绕流区形成旋涡，进一步在旋涡中心出现液体脱落现象，使得其中流体质点的速度为0。

在啮合齿面油膜的密封作用下，间隙最小处出现断流。经计算，啮合区的最大泄漏量为0.16 L/min。

4 验证试验

为了检验数值计算模型的适用性及仿真结果的准确性，采用容积式试验装置进行验证。见图10。

I.动力柜 II.试验台 III.控制柜 IV.工控机

1.油箱 2.液位液温计 3.过滤器 4.截止阀 5.变频电机 6.电磁溢流阀 7.比例减压阀 8.压力表1 9.压力表2 10.数字流量计1 11.数字流量计2 12.单向阀 13.压力传感器 14.测试泵 15.扭矩转速传感器

I. Power cabinetII. Test benchIII. Control cabinetIV. Industrial personal computer

1.Tank 2.Liquid level temperature gauge 3.Filter 4.Shutoff valve 5.Frequency conversion motor 6.Electromagnetic relief valve 7.Proportional pressure reducing valve 8.Pressure gauge 1 9.Pressure gauge2 10.Digital flowmeter1 11.Digital flowmeter2 12.Check valve 13.Pressure sensor 14.Test pump 15.Torque speed sensor

图10 容积式泵试验装置

Fig.10 Volumetric pump test set

图10对应的传感器信息如下：压力传感器13的型号为FB3351GP0S22M3，主要特征为测量瞬时压力的高精度压力传感器，测量精度±0.5%；压力表8的型号为YN﹣320﹣IV，主要特征为检测静压，测量精度±1%；数字流量计10的型号为FBLZJ-40-165J0，主要特征为检测稳态流量的齿轮流量计，测量精度1.0 IR*；扭矩转速传感器15的型号为JC2C，主要特征为实时检测扭矩与转速，用于测量输入功率，扭矩测量精度0.2%，转速测量精度±1 r/min。

试验内容包括在工作压力变化时工作流量的采集以及输入扭矩与转速的获取。试验步骤如下：

1）在空载条件下启动变频电机，同时设定转速为2 000 r/min。

2）待转速稳定后缓慢调节比例减压阀的输入信号，改变负载进而消耗液压能达到油液升温的目的，保持油温为40 ℃。

3）缓慢调节电磁溢流阀操作手柄，使得工作压力为7.5 MPa，同时采用流量计记录工作流量以及采用扭矩转速传感器分别记录瞬时扭矩和转速。

4）重复上述过程2～3次，分别记录压力为7.5 MPa时的流量、扭矩及转速。根据试验过程中记录的数据，取平均值后分别计算容积效率及总效率，对比仿真值和试验值，结果见表5。

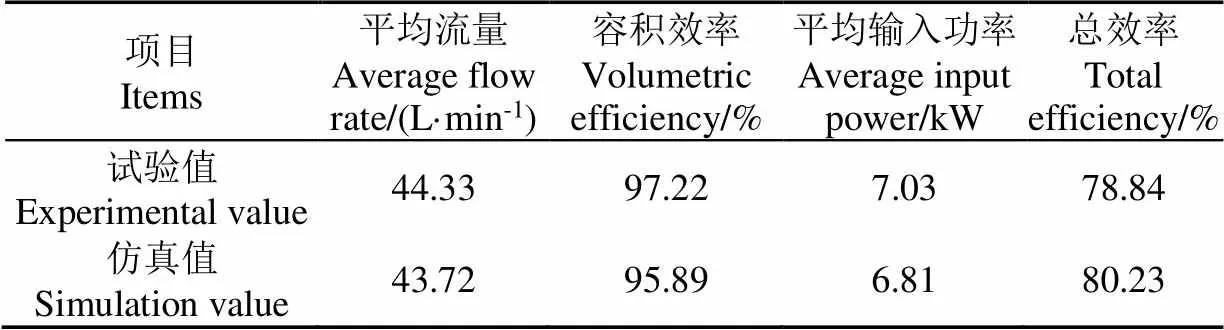
表5 试验和仿真数据对比

由表5可知，试验与仿真的容积效率相差1.33个百分点，偏差率为1.36%；试验与仿真的总效率相差1.39个百分点，偏差率为1.73%。究其原因主要为：油液中的含气量未知、试验中存在测量误差、电动机转速并非恒定、仿真时未考虑零件碰撞损失及油温分布不均匀等。

5 结 论

1）在1/3周期内的瞬时体积流量与瞬时输入功率曲线均呈现连续周期性变化，两条曲线都有4个脉动，这与该段时间内齿轮副的啮合次数一致，进一步说明在齿轮副啮合过程中瞬时流量与瞬时功率都存在最值。

2）由于理论分析无法全面考虑油液实际流动过程而导致总泄漏量的理论值与仿真值相差60.11%，总黏性摩擦功率损失的理论值与仿真值相差66.67%。为了得到更加精确的数学模型，该研究对总泄漏流量以及总黏性摩擦损失数学模型进行修正，修正系数分别为2.5与3。

3）在构成内流道的若干个区域中，静态区域中流线相互平行，油液流动呈现层流状态；质点速度大小基本相同，其中进口流道中速率为1 m/s，出口流道中速率为2 m/s。转子区及交汇区的油液流动呈现湍流状态，速度梯度变化剧烈，其中最高速率超过12 m/s，最低速率小于3 m/s。

4）压差流沿着新月形隔板内外两侧壁面以超过12 m/s的速度逆时针运动，而剪切流沿着外齿轮及内齿圈的外壁同样以超过12 m/s的速度顺时针运动，这样在完全参与密封的齿间出现不同尺度的旋涡，而旋涡中心的液体脱落现象使得其中流体质点的速度为0。

5）在啮合齿面油膜的密封作用下，间隙最小处呈现出断流情形，啮合区的最大泄漏量为0.16 L/min，进一步说明啮合区的密封效果良好，从而达到了与实际流动过程相符的目标。

6）试验与仿真的容积效率相差1.33个百分点，偏差率为1.36%；试验与仿真总效率相差1.39个百分点，偏差率为1.73%，在客观因素限制的条件下偏差值在误差允许范围之内，进一步说明了数值计算模型的适应性及仿真结果的准确性。

[1] 钱隆. 直线共轭内啮合齿轮泵流量脉动特性研究[D]. 兰州：兰州理工大学，2020.

Qian Long. Research on Flow Pulsation Characteristics of Straight Line Conjugate Internal Gear Pump[D]. Lanzhou: Lanzhou University of Technology, 2020. (in Chinese with English abstract)

[2] 柴红强. 直线共轭内啮合齿轮泵的性能分析与仿真研究[D]. 兰州：兰州理工大学，2015.

Chai Hongqiang. Performance Analysis and Simulation Research of Straight Line Conjugate Internal Meshing Gear Pump[D]. Lanzhou: Lanzhou University of Technology, 2015. (in Chinese with English abstract)

[3] 柴红强，杨国来，刘小雄，等. 油液属性对直线共轭内齿轮泵流动特性的影响[J]. 华中科技大学学报（自然科学版），2022，50(4)：19-25.

Chai Hongqiang, Yang Guolai, Liu Xiaoxiong, et al. Influence of oil properties on flow characteristics of straight line conjugate internal meshing gear pump[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2022, 50(4): 19-25. (in Chinese with English abstract)

[4] Kadivar E, Timoshevskiy M V, Nichik M Y, et al. Control of unsteady partial cavitation and cloud cavitation in marine engineering and hydraulic systems[J]. Physics of Fluids, 2020, 32(5): 210801-210820.

[5] Favrel A, Pereira J G, Landry C, et al. Dynamic modal analysis during reduced scale model tests of hydraulic turbines for hydro-acoustic characterization of cavitation flows[J]. Mechanical Systems and Signal Processing, 2019, 117: 81-96.

[6] 杨树军，褚捷豪，彭增雄，等. 液压机械无级变速装载机工况在线识别方法[J]. 农业工程学报，2022，38(4)：1-11.

Yang Shujun, Chu Jiehao, Peng Zengxiong, et al. Online identification method for wheel loader working condition with hydro-mechanical continuously variable transmission[J] Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(4): 1-11. (in Chinese with English abstract)

[7] 史丽晨，李坤，王海涛，等. 拖拉机行星齿轮箱故障响应特性动力学仿真及验证[J]. 农业工程学报，2018，34(7)：66-74.

Shi Lichen, Li Kun, Wang Haitao, et al. Fault response characteristics of tractor planetary gearbox based on dynamical simulation and its validation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(7): 66-74. (in Chinese with English abstract)

[8] 黄溧震. 直线-共轭线型内啮合齿轮泵齿廓分析[J]. 机械传动，2004，28(6)：16-18.

Huang Lizhen. Tooth profile analysis of linear-conjugate linear internal gear pumps[J]. Journal of Mechanical Transmission, 2004, 28(6): 16-18. (in Chinese with English abstract)

[9] Sung H, Min H, Nam Y, et al. Design and experimental verification of a port plate in a gerotor pump to reduce pressure pulsation[J]. Journal of Mechanical Science and Technology, 2018, 32(2): 671-678.

[10] Zhao X, Vacca A. Numerical analysis of theoretical flow in external gear machines[J]. Mechanism and Machine Theory, 2017, 108: 41-56.

[11] Rundo M. Theoretical flow rate in crescent pumps[J]. Simulation Modelling Practice and Theory, 2017, 71: 1-14.

[12] Rundo M. Models for flow rate simulation in gear pumps: A review[J]. Energies, 2017, 10(9): 1261.

[13] Rabsztyn D, Klarecki K. Experimental tests of pressure pulsation of gear pumps[C]// Proceedings of the 13th International Scientific Conference, Gliwice, Poland: Wrocław, Poland AG Press, 2017: 461-469.

[14] 崔建昆，秦山. 直线共轭内啮合齿轮泵的流量脉动分析[J]. 机械设计，2004，21(1)：157-158.

Cui Jiankun, Qin Shan. Analysis of flow pulsation in a linear conjugate internal gear pump[J]. Journal of Machine Design, 2004, 21(1): 157-158. (in Chinese with English abstract)

[15] 段刚，崔建昆，高铭良. 直线共轭内啮合齿轮副的重合度研究[J]. 上海理工大学学报，2018，40(4)：335-341.

Duan Gang, Cui Jiankun, Gao Mingliang. Contact ratio of an internal meshing gear pair with a straight line tooth profile out gear[J]. Journal of Shanghai University of Science and Technology, 2018, 40(4): 335-341. (in Chinese with English abstract)

[16] 顾坤隆，汪中厚，李刚，等. 基于遗传算法的直线内啮合齿轮泵参数优化[J]. 电子科技，2017，30(6)：39-42.

Gu Kunlong, Wang Zhonghou, Li Gang, et al. Optimization of geometric parameters of the straight conjugate internal gear pump based on GA[J]. Electronic Science and Technology, 2017, 30(6): 39-42. (in Chinese with English abstract)

[17] 高铭良，崔建昆，黄冬平，等. 直线共轭内啮合齿轮传动重合度的计算分析[J]. 流体机械，2017，45(2)：28-31.

Gao Mingliang, Cui Jiankun, Huang Dongping, et al. The calculation analysis of contact ratio for straight conjugate internal gear transmission[J]. Fluid Machinery, 2017, 45(2): 28-31. (in Chinese with English abstract)

[18] Chai H Q, Yang G L, Wu G G, et al. Research on flow characteristics of straight line conjugate internal meshing gear pump[J]. Processes, 2020, 8(3): 26901-26928.

[19] 许耀铭. 油膜理论与液压泵和马达的摩擦副设计[M]. 北京：机械工业出版社，1987：23-47.

[20] Chai H Q, Yang G L, Wu G G, et al. Analysis of straight conjugate internal gear pump through numerical modeling and experimental validation[J]. Plos One, 2022, 17(7): e0270979.

[21] 王霞琴，邓龙，柴红强，等. 变工作条件下齿轮泵特性分析[J]. 液压与气动，2022，46(8)：178-188.

Wang Xiaqin, Deng Long, Chai Hongqiang, et al. Characteristics analysis of gear pump under variable working conditions[J]. Chinese Hydraulics & Pneumatics, 2022, 46(8): 178-188. (in Chinese with English abstract)

[22] Wu G G, Yang G L, Cao C C, et al. Analysis of flow characteristics of straight conjugate crescent gear pump at variable working conditions[J]. Mathematical Problems in Engineering, 2022, 2022: 9535319.

[23] Sedri F, Riasi A. Investigation of leakage within an external gear pump with new decompression slots: numerical and experimental study[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2019, 41(5): 22401-22412.

[24] 段志善，田庆飞，郭宝良. 流体介质对齿轮泵内部流场影响的仿真分析[J]. 机械设计与制造，2019，57(6)：132-135.

Duan Zhishan, Tian Qingfei, Guo Baoliang. Simulation analysis on the influence of non-linearity of oil on internal flow field of gear pump[J]. Mechanical Design and Manufacturing, 2019, 57(6): 132-135. (in Chinese with English abstract)

[25] Zhao X, Vacca A. Analysis of continuous-contact helical gear pumps through numerical modeling and experimental validation[J]. Mechanical Systems and Signal Processing, 2018, 109: 352-378.

[26] Rituraj F, Vacca A. External gear pumps operating with non-Newtonian fluids: modelling and experimental validation[J]. Mechanical Systems and Signal Processing, 2018, 106: 284-302.

[27] 吴晓明，王小鹏，马立瑞. 基于集中参数法内啮合齿轮泵AMESim模型的建模方法与仿真研究[J]. 液压与气动，2017，40(7)：103-109.

Wu Xiaoming, Wang Xiaopeng, Ma Lirui. Modeling and simulation based on lumped parameter method by amesim for internal gear pump[J]. Chinese Hydraulics & Pneumatics, 2017, 40(7): 103-109. (in Chinese with English abstract)

Model construction of the internal leakage and viscous friction loss of crescent internal gear pump

Chai Hongqiang1, Yang Guolai1※, Liu Xiaoxiong2, Liu Binghao3, Shi Youcheng1

(1.,,730050,; 2.215000,; 3.,,730070,)

The flow characteristics can be expected to precisely characterize in the crescent internal gear pump. In this study, the mathematical models were developed for the internal leakage and viscous friction loss of the crescent internal gear pump, according to the hydrostatic support oil film theory and Newton's friction theorem. A CFD simulation model with the two-phase flow and dynamic grid was constructed to analyze the flow characteristics of the gas containing oil using the structural parameters and real flow characteristics of the gear pump. A comparison was made on the simulation and theoretical calculations. A series of experiments were carried out to verify the model. The results demonstrate that the continuous periodic variations were observed in the instantaneous volume flow rate and instantaneous input power curves in the 1/3 cycle. Four pulsations of both curves were also found to commensurate with the number of gear pair meshing during this time. 60.11% between the theoretical and simulation values was found for the total leakage flow, and 66.67% was for the total viscous friction power loss. Once the streamline was parallel in the static zone in the laminar particle flow, there was the entirely turbulent in the moving region. The shear flow also moved clockwise at a speed of more than 12 m/s along the outer walls of the outer gear and the inner gear ring, while the differential pressure flow moved counterclockwise at a speed of more than 12 m/s along the inner and outer walls of the crescent diaphragm. Several scale vortices were observed between the fully sealed teeth. The fluid velocity inside the vortex was zero, due to the liquid dropping off near the core. The flow was stopped off at the minimum clearance under the sealing effect of the oil layer on the meshing gear surface, where the maximum leakage in the meshing area was 0.16 L/min. The deviation rate was 1.36% for the volumetric efficiency difference between the test and simulation. By contrast, the deviation rate was 1.73% for the overall efficiency difference, indicating the acceptable error range. As such, a precise mathematical model was proposed for the flow characteristics of crescent internal gear pump. The applicability of the numerical calculation model was validated to assess the accuracy of the simulation. These findings can be used as a guideline to enhance the design theory and examine the internal flow field.

gear pump; test; internal leakage; viscous friction loss; dynamic mesh; multiphase flow

10.11975/j.issn.1002-6819.2022.21.004

TH325

A

1002-6819(2022)-21-0024-09

柴红强，杨国来，刘小雄，等. 新月形内齿轮泵内部泄漏与黏性摩擦损失模型构建[J]. 农业工程学报，2022，38(21)：24-32.doi：10.11975/j.issn.1002-6819.2022.21.004 http://www.tcsae.org

Chai Hongqiang, Yang Guolai, Liu Xiaoxiong, et al. Model construction of the internal leakage and viscous friction loss of crescent internal gear pump[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(21): 24-32. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2022.21.004 http://www.tcsae.org

2022-05-31

2022-09-23

甘肃省青年科技基金项目（21JR7RA270）

柴红强，博士，研究方向为现代液压元件及电液控制系统。Email：chaihq35@163.com

杨国来，教授，博士生导师，研究方向为流体传动与控制应用。Email：yanggl@lut.cn