树木动力特性的实测和有限元分析研究
李正农, 赵 帝, 钟 旻, 吴红华, 陈 斌, 徐海杰
(1.湖南大学 建筑安全与节能教育部重点实验室,长沙 410082;2.河北建筑工程学院 土木工程学院,河北 张家口 075000)
众所周知,树木不仅可以调节气候、避免水土流失,还能够改善自然生态环境,对城市空气净化和改善市容市貌等方面都能起到十分重要的作用。但树木也是脆弱的,在强风的作用下易发生折断倒伏。1999年第14号台风,在登陆厦门时造成了市区行道树的严重破坏,3万株行道树中有近75%受损,其中倒伏1.3万株,折枝1万株[1],造成了巨大的经济损失。因此,有必要对树木的动力特性进行研究,作为其风致动力响应分析及风灾防护研究的基础。
在1962年,Sugden[2]就已经通过有节奏的推拉,采用秒表法测量了红松和白松的自振周期,并提出该参数与树木的直径和高度之比有较好的相关性。后来,Milne[3]在苏格兰的人工种植园里通过人工摇动6棵云杉确定了它们的自振频率及阻尼,研究了其随外形的变化规律,并使用一个简单的公式来预测自振频率。James[4]同样通过拉拔试验确定了一棵银槭树的频率和阻尼,并逐渐去除树枝进行测量,最后发现只有当大于80%的树枝被去除后,才会观察到其振动频率和阻尼的显著变化。在国内,陶嗣巍[5]通过外力拉拔分别测得了毛白杨在自然状态、根土摩擦和固端约束时的基频,并进行了相应情况下的有限元模拟研究。除此之外,还有学者对自然风作用下树木的响应进行了研究。Hassinen等[6]对一棵高11.1 m的树进行了实际风况下的监测,他发现自然风下树木的运动比拉拔试验中要复杂的多,功率谱中有着明显的多个峰值。后来,Schindler等[7]又测量得到了树木在自然风下的多阶振动频率,并进行了树木在有叶和无叶时的频率比较,近似得到了树木振动的前四阶振型[8]。
除了现场实测,数值模拟也是进行树木动力特性探究的重要手段,且能更好地解释实测结果。在早期,通过建立简化的数学模型,使用底部固支的变截面杆来模拟树木[9]。为了考虑树冠的质量,Spatz等[10]在变截面杆的顶部加上了集中质量,并和实测频率进行了对比。但是,树的动态响应涉及到树的每个组成部分的复杂交互作用,分支的影响更像是调谐质量阻尼器,而不是简单的集中质量[11]。因此,近年来有越来越多的学者开始使用有限元方法来构建复杂的树木模型。Moore等[12]便按实际树干、树枝的形状构建了有限元模型,探讨了树冠质量与其自振频率的关系。Ciftci 等[13]以糖枫树为研究对象建立模型,并研究了分支长细比、数量等对其自振频率的影响。
由上可知,前人已经在树木的动力特性研究上有了很大的进展,但是他们一般仅聚焦于树木基频的研究,且未有对其振型的探讨,得到的树木动力特性并不明朗。因此,本文在前人研究的基础上,对一棵柳树进行了力锤激励模态实测和自然风激励模态实测,得到了树木的多阶振动频率、局部振型和阻尼比,并结合有限元模拟,进行了详细的树木振动特性分析。
1 试验概况
1.1 试验仪器
在本次试验中,树木的振动情况由加速度传感器进行测量,如图1(a)所示,使用由江苏东华测试有限公司所提供的 DH105E 型压电式加速度传感器,其量程为50 m·s2,频率范围0.2~1 000 Hz,灵敏度100 mV/m/s2,能较好的满足试验需求。相应的数据采集设备,如图1(b)所示,分别为武汉市优泰软件有限公司生产的UT4516 恒流源适调器、UT3332 采集器以及中国地震局工程力学研究所SP991 型16 线放大器,三者配套使用能得到较为真实精确的信号。最后使用优泰数据采集软件进行采集,由于本次分析频率在100 Hz以内,故将采样频率设为256 Hz,满足香农采样定理。
力锤激励模态试验中采用力锤作为激励源,选用由江苏东华测试有限公司所生产的LC02号力锤,如图1(c)所示,其灵敏度为4.5 pC/N,谐振频率超过22 kHz,量程5 000 N,锤头选用橡胶锤头,以提供宽带频率的脉冲冲击,同样使用前述采集系统进行力信号的采集。

图1 实测仪器Fig.1 The measurement instrument
1.2 试验对象及方法
本次试验于2019年11月份,在河北省张家口市河北建筑工程学院的校园内进行。如图 2所示,以校园内一棵四周较为空旷的柳树为目标,表1为该树的几何参数,能看出该棵柳树有着较为茂密的树冠结构,分别对其进行力锤激励试验和自然风激励试验。

表1 柳树外形几何参数Tab.1 Geometric parameters of willow shape m
力锤激励模态试验选在无风时进行,以减少外部环境对模态试验结果的影响。试验采用MISO方法,即多点激励单点响应,而由于树木的树冠结构复杂,不适宜于模态试验,因此仅进行了柳树树干处的模态测试,分别测试树干在东西方向和南北方向的模态,现场试验情况如图3所示。实测时将加速度传感器布置在树干上距离地面0.9 m 的位置处且在树干沿根部以上每间隔0.2 m 处设置一个激励点,最高点在2.8 m处,共计14个点,依次用力锤从下到上敲击激励点,同时采集加速度传感器信号和激励力信号。

图3 力锤激励模态实测现场Fig.3 Field measurement of hammer excitation mode
柳树的自然风激励试验在力锤激励试验后不久进行,激励力为自然风,因为试验期间主要为西北向来风,因此同样将加速度传感器布置在树的西北向。实测情况如图4所示,因为柳树树干在离地2.8 m高度处存在凸起,不宜放置加速度传感器,故依次将加速度传感器放置在离地0.4 m,0.8 m,1.2 m,1.6 m,2.0 m,2.4 m,2.7 m处,共计7个传感器,采样频率同样设为256 Hz,测量时同时进行所有测点的信息采集。

图4 自然风激励的模态实测现场Fig.4 Natural wind excitation mode field measurement
1.3 实测结果及分析
对于力锤激励试验,分别对东西方向和南北方向的实测数据进行分析,利用MATLAB软件得到所有测点的功率谱如图5所示,采用双对数坐标的形式,横坐标为频率,纵坐标为自功率谱密度。功率谱曲线的峰值较为平缓,从中可大致识别出前七阶主要振动频率,如表2所示。接着利用和实测配套的优泰分析软件进行频响函数曲线的构建,得到相应自振频率处的阻尼比(见表2)和树干处局部振型如图6所示。能看出柳树东西向和南北向的频率稍有不同,这和柳树的结构形态有关,因为树木生长时会受到周围环境影响,而并非是完全对称的结构,因此不同方向的振动特性会有所不同,但也能看到其差别并不大,故而也能按照同阶模态处理。阻尼比通过半功率带宽法进行计算,类似于James和Kane等[14]的结果,柳树的各阶阻尼比也大致在10%~20%,其阻尼比相对较大。其原因可能是:首先,由于柳树的树冠结构宽大,树叶也较为茂密,所受的气动阻尼力也相应较大;其次,由于树枝间的复杂交互作用,树枝的质量也会发挥着动力阻尼的作用,进一步的增大了树木的阻尼。除此之外,也能看出柳树东西向和南北向的阻尼比结果也稍有差异,这也和Kane等的实测结果相似,同样分析为是由于柳树结构东西向和南北向的结构差异所产生的。

图5 力锤激励试验所有测点的功率谱Fig.5 The power spectrum of all measuring points in the hammer excitation test
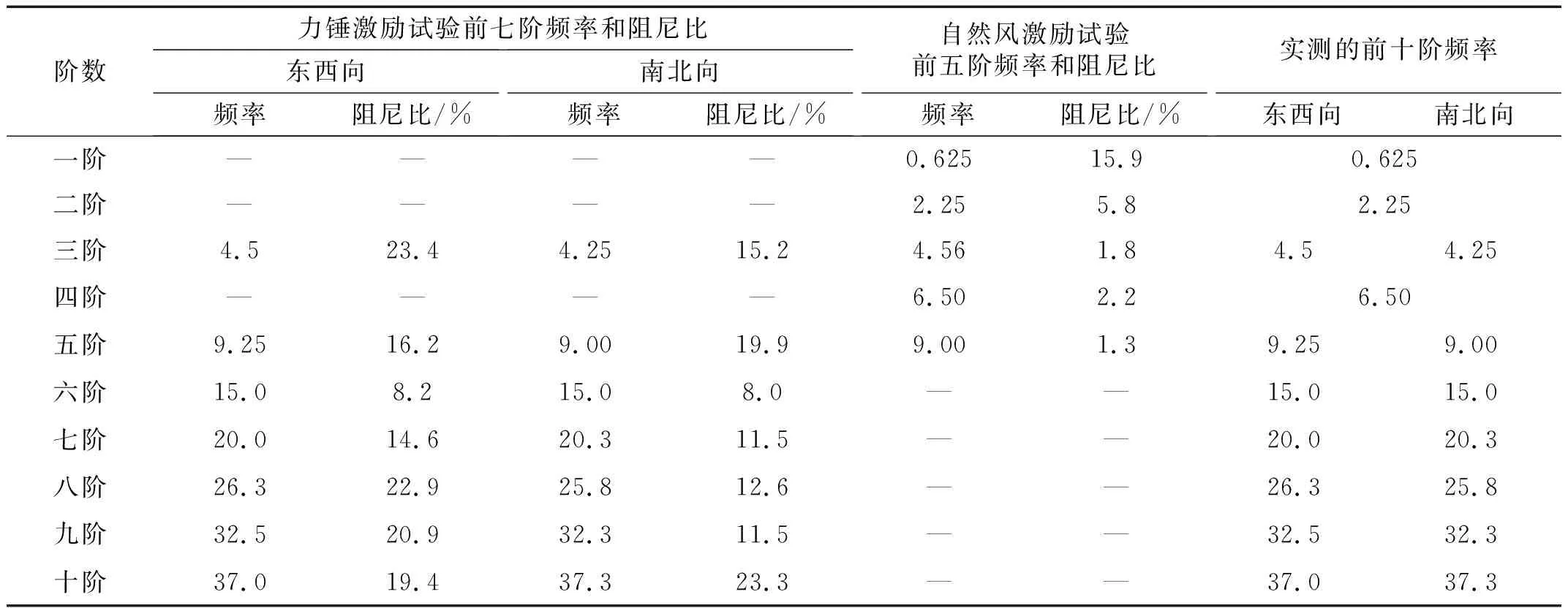
表2 柳树的实测频率和阻尼比Tab.2 The measured frequency and damping ratio of willows

图6 力锤激励试验所得的前七阶局部振型Fig.6 The first seven local modes obtained from the hammer excitation test
自然风激励试验测量了柳树在自然风下的振动情况,其中,列出32 s内在树干2.7 m高度处加速度传感器的响应情况如图7所示,能明显看出该柳树在风荷载作用下存在着周期运动。利用MATLAB软件同时对7个加速度传感器的时程数据进行功率谱计算,结果如图8所示,功率谱采用双对数坐标显示,横坐标为频率,纵坐标为自功率谱密度。能看出其振动能量主要处于低频段,而高频处的振动能量极小,相应的高频振动结果也较为紊乱,因此在分析时仅分析柳树在10 Hz前的振动频率。从中可以较为明显的得到该棵柳树的前五阶频率,见表2,由于加速度传感器仅置于树木的西北向,因此也仅能得到一个方向的振动频率。从功率谱结果中能较明显的看出自然风激励下柳树在10 Hz前的树干局部振型均有着悬臂梁的一阶振型,这也和力锤激励下的实测结果一致。同样利用半功率带宽法计算阻尼比(见表2),发现第一阶频率处阻尼比要比其余阶较大,这是因为树木在自然风中吸收的大部分能量都是通过第一阶模态振动来耗散的,所以其阻尼比也会较大。另外,自然风激励试验在的4.5 Hz、9 Hz处阻尼比明显小于力锤激励试验相应频率处的阻尼比,这是因为在频率密集的频段,实测所识别出的频率会存在相互耦合[15],树木则由于树枝的存在其频率分布较为密集,而力锤激励法主要激励的为树干,而并不能较好的激励出树冠部分的动力响应,实测所得结果可能为多个固有频率的耦合值,使功率谱中各个峰值较为平缓,所以在使用半功率带宽法计算其阻尼比时,所得结果会偏大;而自然风激励多作用于树冠,能较好的激励树枝的振动,实测结果的耦合效应较小,从而导致阻尼比偏小。
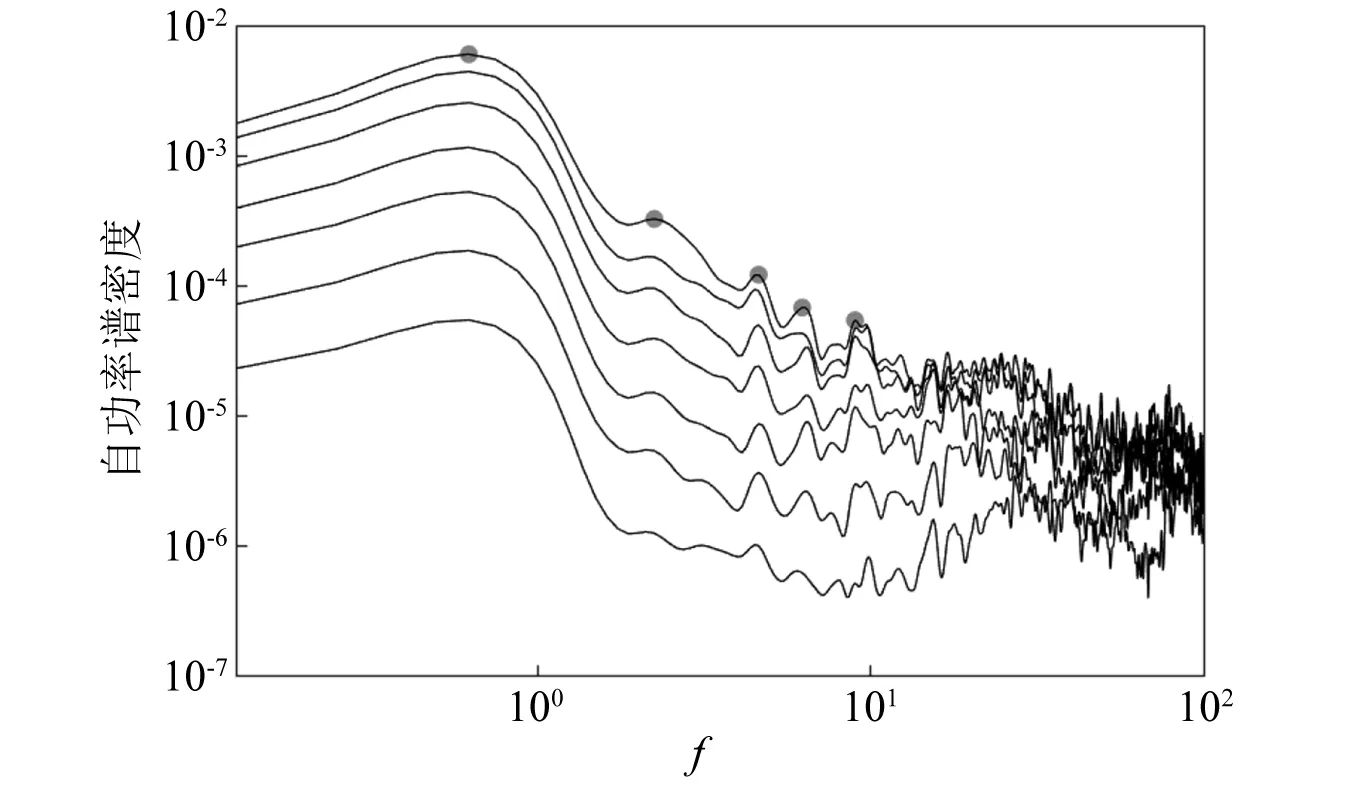
图8 柳树在自然风激励下的功率谱Fig.8 Power spectrum of willows under natural wind excitation
从力锤激励试验和自然风激励试验的结果来看,两个试验所得到的各阶频率间存在差异,但自然风激励试验的第三阶、第五阶和力锤激励试验的第一阶、第二阶频率极其接近。而结合其余学者的研究成果,发现树木的基频均低于2 Hz,而且该柳树也有着较为茂盛的树冠结构,再结合后文中的有限元模拟结果,可认为力锤激励试验得到的柳树模态结果有所缺失。这也和贺磊盈[16]论文里的结果相同,她对一棵山核桃树进行了力锤激励试验和有限元模拟,实测结果也缺失了树木在5 Hz以内的振动频率。
为分析造成这种结果的原因,同时绘制出力锤激励试验和自然风激励试验的功率谱,如图9所示,其中由于力锤试验东西向和南北向结果相近,因此仅列出力锤试验的东西向结果。从中能看出,首先在激励力的总能量上,自然风能量要远大于力锤冲击力的能量,其功率谱最高处的能量(6×10-3)几乎要比力锤激励的最高处能量(1×10-4)大两个量级,在实测时也易发现柳树在自然风下有着较大的运动,而在力锤激励下柳树仅是稍微振动。其次,从激励力的能量分布上看,自然风频率主要集中于低频(0.1 Hz以内),主要激励的为柳树的低频振动模态,从功率谱中也能看出,自然风激励下柳树在0.625 Hz处有最大响应;而本次力锤在采用橡胶锤头时,其冲击力虽有着较广的带宽,但在低频处能量较少,使柳树在低频时的振动响应较小,但也能看出其高频响应较大,甚至高于了树木在自然风激励下的高频响应能量,也因此力锤激励试验才能激励出柳树的高阶振动模态。
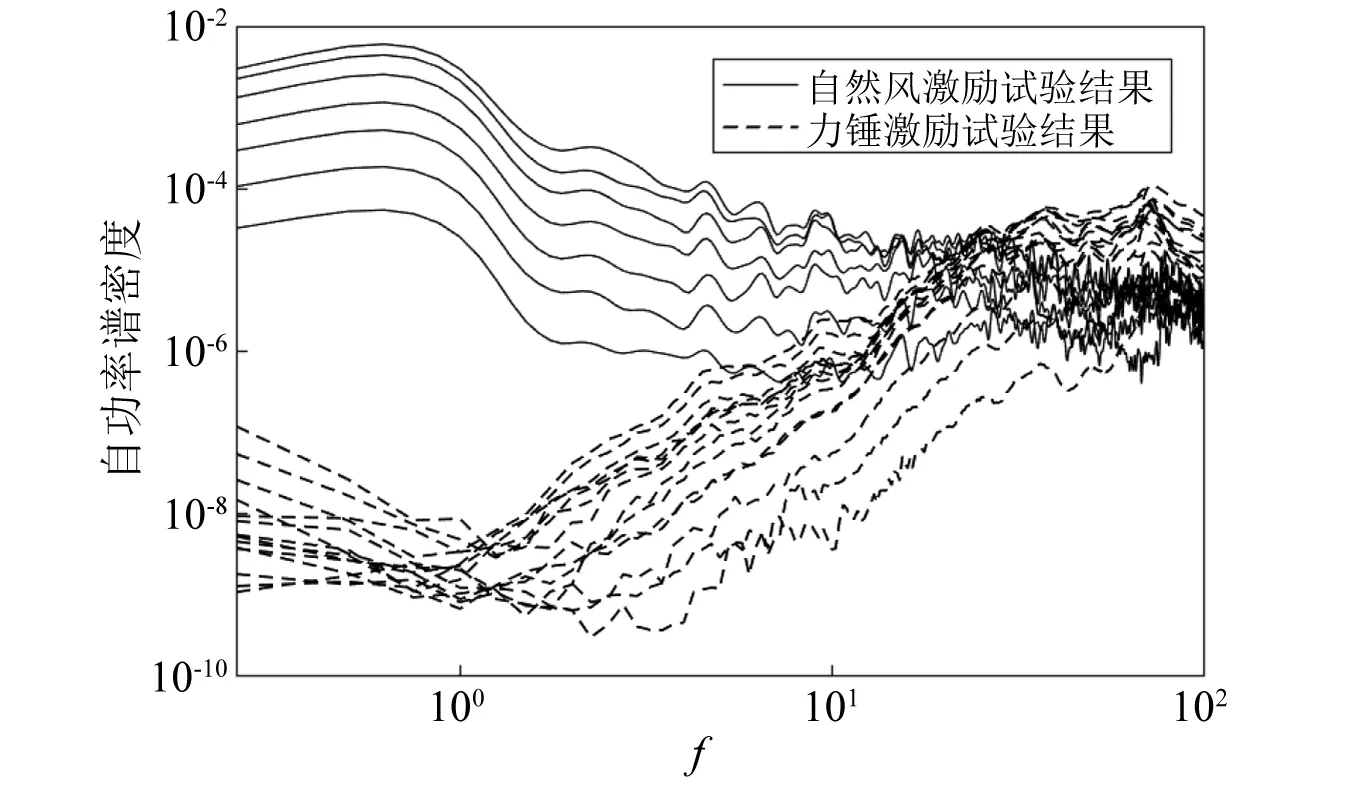
图9 力锤激励和自然风激励试验的功率谱对比Fig.9 Comparison of power spectrum between hammer excitation and natural wind excitation
因此,综合两种试验的结果来共同组成柳树实测的前十阶模态,得到前十阶频率见表2。其中,自然风激励试验的第三阶、第五阶和力锤激励试验的第一阶、第二阶频率极其接近,两者相差最大仅为0.3 Hz,可认为属于正常的试验误差,仍可将其当作同一阶频率来考虑;另外也由于力锤激励试验同时得到了柳树在东西向和南北向这两个方向的模态,结果更为全面,因此在实测的第三阶、五阶处选用力锤激励试验的结果。
2 有限元模拟
2.1 模型的构建
有限元模拟对复杂结构的适用性较强,并能帮助更好地理解、分析实测数据,逐渐成为国际上的研究趋势。但是实际树木拥有较多的枝条和树叶,其复杂性远远超过了一般结构。完全按照实际树木结构进行建模是不现实的,也是不必要的。国内外众多学者为此进行了不同程度的简化,本文依据前人经验,根据柳树的形状,仅保留树木的一级分支和主要二级分支,而将其余结构作为集中质量加在模型的相应位置。
树木的材料特性复杂,其本身为非均质、各项异性材料,但为了研究方便一般视为各向同性。受含水率和生长周期影响,同棵树木不同位置的弹性模量和密度也存在差别,但密度的变化相对较小,而弹性模量的变化较大[17-18]。因此本次建模时假设整棵柳树的密度为常数,而将树干和树枝的弹性模量取不同的数值,大致取树枝弹性模量为树干的0.8倍。其中,由于柳树在离地2.8 m高度处出现分化,因此将2.8 m高度以上结构均视为树枝材料。另外,根部约束若按固定端约束考虑,可能会有较大误差,而弹簧约束则更符合树木的实际受力情况[19],因此本文也使用弹簧约束,设置为柳树模型根部沿X向和Y向的旋转弹簧。参考Jonsson等[20]在论文中所得到的树木胸径和根部锚固刚度的关系,并结合实测得到的柳树振型结果,综合取根部锚固刚度为1 000 kN·m/rad。
实际建模中,使用ANSYS有限元软件,按照实际柳树结构来进行模型的构建,以东西方向作为X轴,以南北方向作为Y轴,模型结果如图10所示。其中,树木树干的尺寸及树枝的基部尺寸均由卷尺测得,而较高处则通过树木实际图像进行测定,建模时使用beam188梁单元,共计1 505个单元;树枝上集中质量由估算得到,使用38个mass21单元进行建模;最后使用两个combin14单元模拟柳树根部沿X向和Y向的抗弯刚度,而完全约束根部其余方向的自由度。具体材料设置如表3所示,密度由《世界主要树种木材科学特性》[21]一书大致确定,而弹性模量由于受生长龄期影响较大[22],文献中柳树木材的弹性模量取值和实测柳树弹性模量会有较大差别,因此需根据实测结果进行调整。根据前人研究,树木整体泊松比取为0.38[23]。

图10 柳树有限元模型Fig.10 Finite element model of willow tree

表3 柳树模型材料参数Tab.3 Material parameters of willow model
2.2 有限元模型结果分析
在有限元软件中,使用Block Lanczos方法进行模态分析,得到各阶频率及扩展模态结果。由于柳树结构树枝数量多,导致模态分析中得到的有限元阶数过多,然而其中大多数频率仅为部分树枝振动所产生的,为局部模态,而非柳树的主要模态。但是现场实测所得结果应为树木的主要模态。因此,为了和柳树实测结果相对应,须先对有限元模型结果进行分析,来剔除模型中的局部模态,确定模型的各阶主要模态。在本次分析中,首先确定模型的各阶频率范围,然后确定每阶频率范围内的主要频率,如此便能得到模型的各阶主要频率和振型。
2.2.1 模型的各阶频率范围确定
不同于悬臂梁结构,树木的自振频率受到各个树枝的相互作用影响,故而其频率的分布较为密集。而相对于细小的树枝,粗大的树枝对树木频率的影响较大。为了探究大树枝对树木频率的影响,本文也进行了简单的简化模型的构建, 如图11所示。该简化模型在原模型的基础上仅完全保留树干和1号枝(1号枝是该柳树最长、最粗的一根树枝,见图10),而将其余树枝的质量全部置于树干的顶部,使该简化模型和原模型的总质量相同,其余参数也完全相同。

图11 简化模型Fig.11 Simplified model
由于该简化模型大致为悬臂梁结构,可以很简单明了的得到前十阶频率如表 4所示,并且因为其X向和Y向频率极其相近,为了简便故在此将其合并为一个频率,不做区分。从表4中能看出,简化模型的前十阶频率和表2中实测柳树各阶频率有着大致的对应,并且其相应位置处的局部振型和实测结果也极其相似(MAC 值均在0.96以上,MAC计算公式见下文),但由于篇幅限制并不在文中列出。因此,能看出在仅保留1号枝的形状时,简化模型便能基本保有柳树结构的主要频率,故而能认为1号枝对柳树的各阶主要振动频率有着较大的影响效应。进而可推断出,柳树结构在主要频率处振动时,柳树整体和1号大树枝应做同阶振动。

表4 简化模型模型的前十阶频率Tab.4 The first ten frequencies of the simplified model
综合以上分析,可将原模型中1号大树枝的阶数(指由1号树枝和树干组成的结构的阶数,后文同理)作为划分柳树模型频率范围的标准。比如,认为所有的1号枝具有第一阶振型的频率,共同组成了柳树模型的第一阶频率范围。因此,根据柳树有限元模型(特指原模型)的各阶振型中1号枝的振动情况,依次划分模型的前十阶频率范围,如图 12所示,其中,X轴为该频率在有限元模型中的阶数,Y轴为该频率的具体数值。从图中能看出,在低频处,树木频率的分布更为密集,有50阶频率均在10 Hz以内。

图12 柳树有限元模型的前十阶频率范围划分Fig.12 The first ten frequency range division of willow finite element model
2.2.2 模型各阶模态的确定和结果分析
在确定了各阶频率范围后,需结合振型参与系数,来确定每阶频率范围内的主要振动频率,进而得到各阶振型。由于振型参与系数为每个质点质量与其在某一振型中相应坐标乘积之和与该振型的模态质量之比,一般来说,振型参与系数越大,该阶模态的动力响应也就越大。因此,在每阶的频率范围内分别选取X向、Y向振型参与系数最大的模态,作为有限元模型在该阶的X向、Y向振动模态。得到模型各阶频率如表5所示,相应的各阶振型如图13所示。
图13 柳树有限元模型的前十阶振型Fig.13 The first ten modes of vibration of willow finite element model

表5 柳树有限元模型的前十阶频率Tab.5 The first ten frequencies of willow finite element model
分析所得的各阶振型结果,发现在柳树模型的各阶模态振型处,主要振动的均为树枝结构,而树干的振动则相对较小。这和柳树的结构形式有关,树枝结构相比于树干较为轻柔,刚度较小,所以振动时便会有着相对较大的位移。特别的,在柳树模型的第一阶模态振型处,树干更是只有极小的振动(该模态处,树干最大振动位移仅为树枝最大振动位移的1.5%)。分析主要为柳树树枝的基础频率(此处仅指树枝杆件,如柳树1号枝的基频0.70 Hz,计算基频时仅保留1号枝,且树枝底部当作固接)要远低于树干的基础频率(仅指树干杆件,如柳树树干结构,计算时仅保留树干,且将树干底部当作固接,得到其基频为7.9 Hz),因此在柳树的第一阶模态(0.654 Hz)处,产生共振的为树枝结构,而树干还远未达到其共振频率,故而只是微微振动。这也和Ciftci等的研究结果类似,树枝的存在才是产生了柳树第一阶模态的主要因素。但是随着柳树振动频率的增加,在逐渐达到树干的自振频率时,树干会逐渐的达到自振,其振动幅度也会越来越大。而这可能也是力锤激励试验缺失部分主要模态的一个原因,因为在这些模态处,树干的振动是极其微小的。
观察模型的前十阶模态,发现在前两阶模态处,所有树枝均做同阶振动(指由各树枝和树干分别组成的结构的阶数);而在之后,各个树枝的振动则逐渐出现分化:首先在模型第三阶模态处,当其余枝均做第三阶振动时,最短的3根枝却仍是第二阶振动;再随着模型模态频率的逐渐增大,长树枝和短树枝的阶数差别越来越大。分析认为,是不同树枝的各阶固有频率的不同所导致的。在柳树中,长枝的高阶固有频率低于短枝的相应阶,使柳树在某一高阶模态频率处振动时,短枝的振动阶数要小于长枝。而也正是不同固有频率的树枝间的相互作用,才造成了复杂的树木整体振动情况。特别的,当柳树多数树枝的固有频率间出现重叠时,也就产生了柳树的主要振动模态。
3 模拟结果和实测结果的对比
3.1 频率对比
在1.3节中已经明确了实测的前十阶频率见表2,并得到了有限元模型的前十阶频率见表5。其中,为定量分析,使用相对误差来进行模型结果和实测结果的各阶频率对比,其计算公式为
(1)
式中:fm为有限元模拟所得频率;fs为柳树实测各阶频率。各阶的相对误差计算结果如表6所示,从表6中可看出,其中大多数阶频率的相对误差值均小于10%,实测和模拟的相对误差在第二阶频率处最大,但也未超过15%,这说明有限元模型和实测的前十阶频率有着较好的相互对应关系。

表6 柳树实测和模型前十阶频率的相对误差Tab.6 The relative errors of the first ten frequencies of willow tree measurement and model %
3.2 振型对比
由于仅力锤激励试验得到了树木X向(东西向)和Y向(南北向)实测振型,即实测的第三、第五、第六、第七、第八、第九、第十阶。因此,可在该七阶频率处,进行有限元模型和实测的局部振型对比分析。有限元模型的各阶整体振型已在图13中列出,现提取模型在树干处的各阶局部振型,保证提取的各点高度和实测测点的高度一一对应,并进行振型归一化处理,得到振型对比结果如图 14所示。
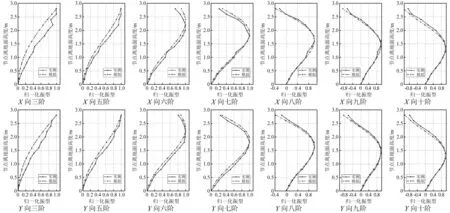
图14 有限元模型和力锤激励实测结果的柳树局部振型对比Fig.14 The comparison of local vibration pattern between finite element model and measured results of hammer excitation
利用 MAC方法(模态置信准则)判断模型与实测振型的相似度,其具体为振型φa和φb的相似度可以应用以式(2)来计算
(2)
计算结果如表7所示,其中 MAC 值越接近1,便说明两个振型越相似。从表中能看出,所有MAC值均在0.96以上,这说明有限元模型和力锤激励试验的各阶局部振型结果极其相似。

表7 利用MAC方法计算得到的振型相似度Tab.7 The MAC method is used to calculate the mode similarity
因此,综合来看,柳树有限元模型的模拟结果能较好的对应于柳树实测得到的各阶频率和振型,这说明构建的柳树有限元模型是准确的,也说明实测得到的前十阶模态便是柳树结构的前十阶主要振动模态。在这些模态处,柳树结构为整体振动,其各个部分均参与振动。
通过有限元模拟结果和力锤激励试验、自然风激励试验结果间的相互对比验证,能明确看出,力锤激励试验结果缺失了多阶低频振动模态,但是也能看出力锤激励试验可较好的激励出树木的高频模态,其得到的后六阶模态便是实际柳树结构的第五阶~第十阶主要振动模态,在有限元模型的构建和后续的结果验证中均有着较大的作用。
通过图13和图14,结合柳树的树干局部振型和整体振型的关系,能看出虽然树干的振型一直处于悬臂梁的一阶振型~二阶振型,但实际的柳树结构其实处于一阶~十阶振动,此时发生较大阶数变动的主要为树枝结构,这说明柳树的树冠结构才是使柳树产生了这十阶振动模态的主要因素,树冠对柳树的动力特性起控制作用。这也和柳树的结构形式有关,柳树的树冠结构较为高大、轻柔,树枝的刚度较小,而树干的刚度则较大,也就使在同阶模态振动时,树干的振动阶数要远小于树枝的振动阶数。
4 结 论
本文以一棵实际的柳树为研究对象,进行了动力特性实测。之后利用有限元方法进行了柳树的数值分析模型构建,深入研究了该柳树的动力特性,具体结论有:
(1)力锤激励试验难以激发出柳树全部的主要振动模态,所得结果缺失了部分低频振动模态,但是其能较好的激励出柳树的高阶模态,对柳树有限元模型的构建起着至关重要的作用;而自然风激励试验则能激励出柳树的低频模态,所得的五阶模态便是柳树的前五阶主要振动模态,能对力锤激励试验结果有着较好的补足。分析造成这两种试验结果不同的原因,主要为:首先,力锤冲击力的能量要远低于自然风激励能量,力锤造成树木的振动响应较小;其次,在能量分布上,自然风频率主要集中于低频,而本次试验的力锤冲击力虽有着较广的带宽,但在低频时的能量分布较少,故而并不能很好的激励柳树的低频模态;最后,力锤冲击力主要作用于树干,难以激发树冠部分的动力响应,因此会缺失以树冠部分振动为主的模态。
(2)按照实际的柳树结构进行了有限元模型的构建,发现大树枝对柳树的动力特性有较大影响,提出了使用模型中大树枝的阶数来划分柳树有限元模型各阶频率范围的方法,进而提取出了柳树的前十阶主要振动频率和振型。通过振型结果分析,发现在柳树的各阶模态振型处,树干的振动相比于树枝均较小;特别在第一阶模态振型处,柳树以树枝振动为主,而树干的振动量极小。
(3)柳树有限元分析结果和实测结果有着较好的对应,说明构建的有限元模型是准确的,也说明实测得到的前十阶模态便是柳树结构的前十阶主要振动模态。通过树干局部振型变化和树木整体振型变化的比较,发现柳树的树冠结构对柳树动力特性有着巨大的影响,柳树整体振动阶数的变化主要由柳树树枝结构的振动阶数变化所产生。

