基于平面波展开法的声学黑洞梁弯曲波带隙研究
李敬, 朱翔,3, 李天匀,3, 万志威
(1.华中科技大学 船舶与海洋工程学院,湖北 武汉 430074; 2.船舶和海洋水动力湖北省重点实验室,湖北 武汉 430074; 3.高新船舶与深海开发装备协同创新中心,上海 200240)
声学黑洞(acoustic black hole,ABH)作为一种新型的高效波被动控制结构,主要通过幂律裁剪截面的形式抑制结构弯曲波的传播,进而实现减振降噪[1-3]。目前对于单个黑洞效应的研究相对集中, Georgiev等[4]在椭圆板焦点处设置声学黑洞,验证了声学黑洞抑制椭圆板振动的有效性。Denis等[5]研究了尖端带声学黑洞梁的反射系数测量方法,实验结果表明声学黑洞能有效地吸收在波束中传播的弯曲波。邓杰等[6]研究了单个声学黑洞梁振动能量分布问题。曾鹏云等[7]研究了一维锥形杆黑洞梁能量聚集效应,表面其尖端聚能效果优于楔形梁结构。何璞等[8]研究了盒式声学黑洞梁振动特性,实现了结构全频带的减振效果。
人工周期性结构形成声子晶体能产生声波带隙,是近年来结构减振降噪的另一思路。有部分学者研究了带声学黑洞的周期性结构,Zhu等[9]对内嵌周期性声学黑洞的薄板的频散特性进行了研究,发现在部分频带出现禁带特性,为高薄壁结构的减振降噪提供思路。刘波涛等[10]通过实验研究了嵌入阵列声学黑洞的薄板的隔声性能,在低频带得到了较好的宽频隔声性能,并给出了一种工程中实用的声学黑洞周期结构。Ganti等[11]探索了基于声学黑洞元素的单位单元设计拓扑弹性波导的可能性,表明声学黑洞单元的使用能够显著简化结构设计并对结构频散特性进行微调,而且更容易产生低频带隙。但这方面研究仍相当匮乏,比如材料特性与声学黑洞周期性的结合。因此本文构建出一种以声学黑洞为原胞的周期性梁,结合材料属性变化,分析结构弯曲波带隙特性。
目前,声子晶体带隙计算方法主要有平面波展开法、传递矩阵法以及有限元法。平面波展开法是通过以平面波的形式将各种参数在倒格矢空间展开为傅里叶级数,将级数代入波动方程得到特征方程,适用范围广。目前对于声子晶体梁的带隙研究大多针对恒定截面梁[12-14],部分学者利用不同的方法研究了变截面梁,付志强等[15]采用近似的集中质量法对弹性纵波在一维指数形截面有限周期声子晶体中的传播进行了研究,何东泽等[16]利用回传射线矩阵法研究了线性均匀变截面声子晶体梁的带隙特性。平面波展开法处理声子晶体问题具有较好的实用性,但利用平面波展开法计算类似声学黑洞的连续变截面梁的弯曲波带隙研究尚未见到,因此本文基于平面波展开法,推导了周期声学黑洞梁基本结构参数的平面波展开形式,给出平面波展开法计算弯曲波带隙的特征方程,为后续周期声学黑洞结构弯曲波带隙研究提供一定的理论基础。
虽然传递矩阵法可得到精确解,但利用传递矩阵法解决此类连续变截面梁问题时,需将原胞分成很多小段,相较于平面波展开法,其计算量与计算时间急剧增加,效率较低,因此仅利用传递矩阵法验证计算结果的准确性。
1 周期声学黑洞结构模型与原理
周期声学黑洞梁结构如图1、2所示,图1是单个原胞结构,即单个黑洞结构,图2是周期黑洞梁结构,由原胞周期延拓形成。
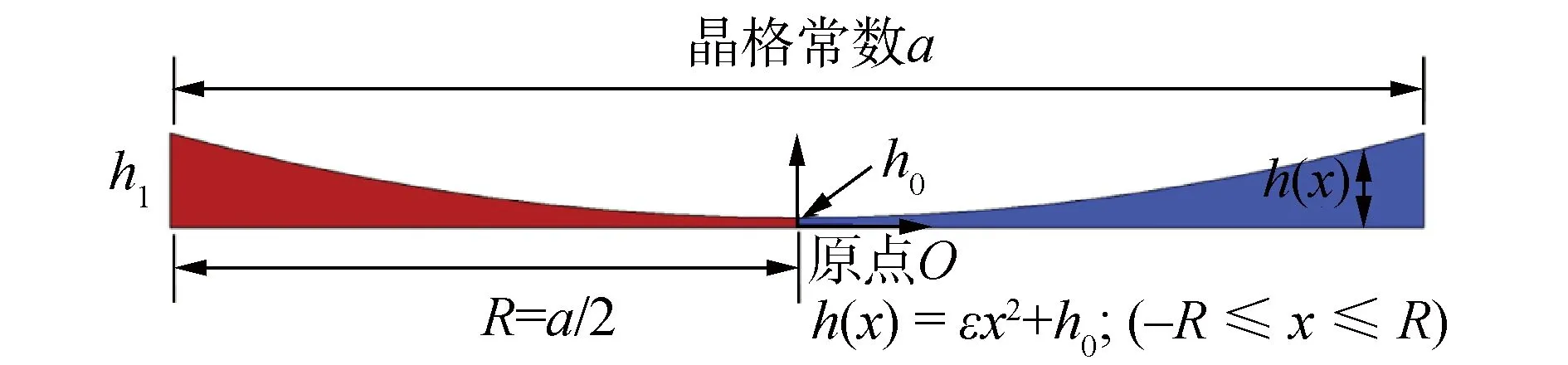
图1 周期声学黑洞梁原胞

图2 周期声学黑洞梁
声学黑洞截面按二次抛物线规律变化:
h(x)=εx2+h0, -a/2≤x≤a/2
(1)

变截面的欧拉梁的自由弯曲振动方程[17]为:
(2)
如图1所示,原胞的中心取为坐标原点,声学式中ρ(x)、S(x)、E(x)、I(x)分别为梁的密度、截面面积、弹性模量和截面惯性矩,均是关于x的位置坐标函数,将其称为结构参数m(x)、y(x,t)为结构弯曲振动位移,并令M(x)=ρ(x)S(x),D(x)=E(x)I(x)表示结构的质量与刚度。
对于周期声学黑洞梁,弯曲波满足Bloch定理,黑洞梁的弯曲振动位移y(x,t)可表示为:
y(x,t)=uk(x)exp[i(kx-ωt)]
(3)
式中:ω是圆频率;k是限制在第一简约布里渊区的波矢;uk(x)是与结构参数具有同样周期的函数,可以通过傅里叶级数展开:
(4)
式中UG1是一维倒格矢G1对应的Fourier系数。
结构参数m(x)具有周期性,也可以展开为傅里叶级数:
(5)
式中MG2是一维倒格矢G2对应的Fourier系数,满足:
(6)
1.1 双材料周期声学黑洞梁
记图1声学黑洞原胞左半段为材料A,右半段为材料B,将结构参数M(x)、D(x)代入式(5)、(6)展开为级数形式,并利用倒格矢的性质:Ga=2nπ,n为整数进行化简得:
(7)
(8)
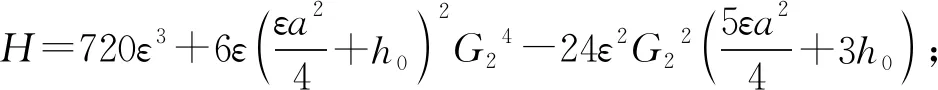

H、C、P、F均为关于G0、ε、h0的表达式。
将式(3)、(4)、(7)、(8)代入式(2),得:
exp[i(kx+G2x+G1x)]
(9)
利用复指数函数的正交性,在等式左右两边同时乘以e-i(G3x+kx)后在一个原胞上对x进行积分,化简得到特征方程:
(10)
式中G3=G1+G2。
G3与G1取遍整个倒格矢空间,式(10)是无限矩阵的特征值问题。为便于分析,实际上选用倒格矢空间的有限个倒格矢代替整个倒格矢空间。对称选取半波轴上n个不过原点的倒格矢进行计算,则总倒格矢有2n+1个,平面波数量为N=2n+1个,则将式(10)转换成N阶的广义特征值问题:
ω2LU=TU
(11)
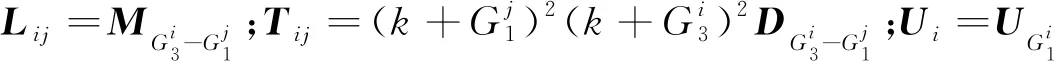
对于图2所示的周期声学黑洞梁,L、T均为实对称矩阵,而且L为实对称正定矩阵。利用实对称正定矩阵的性质,则由式(11)求出的广义特征值ω2一定为实数,即方程必定有解。
1.2 纯周期声学黑洞梁
当结构中原胞材料相同时,结构参数中的密度ρ(x)与弹性模量E(x)为常数,即:ρA=ρB=ρ,EA=EB=E。将此种声学黑洞原胞周期延拓形成的周期梁称之为纯周期声学黑洞梁。此时需对截面惯性矩I(x)与截面面积函数S(x)展开成傅里叶级数,式(7)、(8)中带ρA-ρB,EA-EB的项均为0。并将E、ρ当公因式提出来。而截面惯性矩I(x)与截面面积S(x)的傅里叶展开级数为:
(12)
(13)
将式(3)、(4)、(12)、(13)代入式(2),并利用复指数函数的正交性,化简得到特征方程:
(14)
2 收敛性分析
对于纯周期声学黑洞梁,分别取4种材料计算各自的带隙特性。4种材料为环氧树脂、有机玻璃、铝和钢。材料属性见表1。对于2种材料构成的声学黑洞梁,选取环氧树脂-铝、环氧树脂-钢、环氧树脂-有机玻璃、铝-钢周期声学黑洞梁4种结构进行分析。
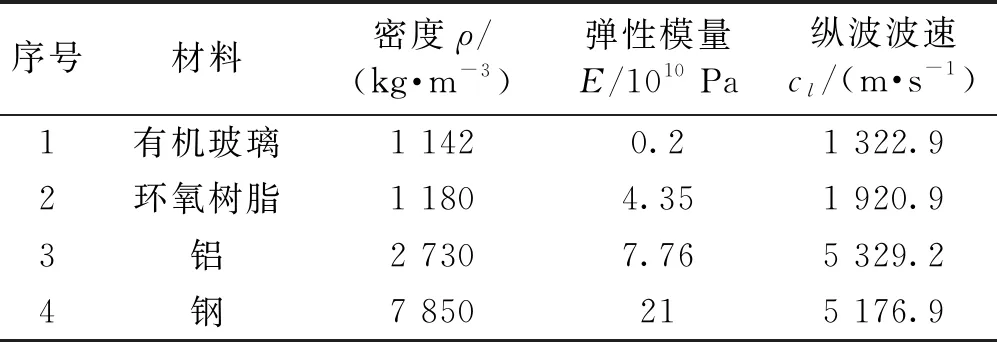
表1 材料属性
黑洞参数为a=0.2 m、h0=1.5 mm、h1=15 mm。截面高度度h(x)随长度x(-R≤x≤R)变化表达式:
1.35x2+0.001 5 m
(15)
对于平面波展开法,平面波数量N的选取影响计算结果的收敛性与精确性,因此首先改变平面波数量计算结构的固有频率以进行收敛性分析。对于本文中的周期黑洞梁,第一布里渊区的中心(k=0)和端点(k=±π/a)的位置是结构的高对称点,是容易使得结构发散的点。因此选取这2个位置进行收敛性分析。
2.1 纯周期声学黑洞梁
对于纯周期声学黑洞梁,结构材料不变。因此仅需选取某种材料构成的梁进行收敛性分析。这里选取环氧树脂梁,对其高对称点处的第3、6阶固有频率进行分析。参数n取值范围为5~60,步长为1,即平面波数量变化范围为:11~121。计算结果如图3所示。
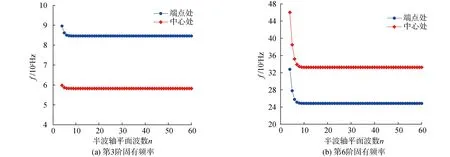
图3 纯周期黑洞梁平面波展开法收敛性分析
当n变化时,端点处和中心的固有频率变化百分比误差小于1%时,认为结果收敛,即选取波数m时结果收敛满足的条件:
(16)
式中fm表示n=m时结构的频率。
从图3中可以看出,利用平面波展开法计算纯声学黑洞梁弯曲波带隙特性时,随着n的增加,固有频率收敛较快。利用式16判断收敛性,当n≥9时,即平面波数量N≥19时可认为结果收敛,从图中也可看出此时结果收敛。
进一步分析可知,收敛较快是由于声学黑洞是连续的幂律变截面结构,且结构没有材料的变化,即结构中没有出现阻抗失配严重的区域,这就导致材料参数通过平面波展开为级数形式时,级数收敛较快,从而选择较少的平面波数量就能得出很稳定的结果。
2.2 双材料周期声学黑洞梁
对于2种材料构成的周期声学黑洞梁,由于组成黑洞结构的2种材料不同,需要对这4种结构单独进行收敛性分析,因此改变平面波数对4种周期黑洞梁的高对称点处的第6阶固有频率进行分析。结果见图4。
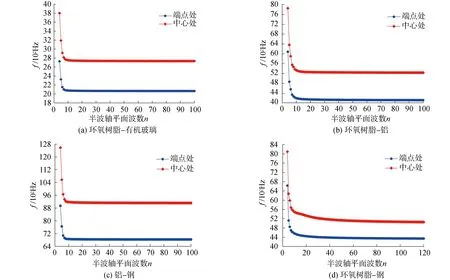
图4 双材料周期黑洞梁平面波展开法收敛性分析
利用式16判断收敛性,环氧树脂-钢质黑洞梁收敛较慢,n≥103时中心点处收敛,n≥61时端点处完全收敛。而环氧树脂-有机玻璃、铝-钢与环氧树脂-铝声学黑洞梁收敛较快,分别在n≥19、n≥35、n≥43时收敛。
从收敛性结果得知,当材料差异较小时,利用较少的平面波就能使结果收敛,而且中心点处收敛较两端慢。这是因为采用平面波展开法计算时,对材料参数进行级数展开,当材料差异较大时,不连续的参数使得傅里叶级数在材料分界面处收敛较慢,甚至可能发散。因此相较于同种材料的声学黑洞梁,2种材料组成的声学黑洞梁收敛需要更多的平面波数,材料差异越明显,需要的平面波数越多。
3 结果分析
根据收敛性分析结果,将波矢k限制在第一布里渊区[-π/a,π/a]内,改变波矢k,为了结果的精确性,计算时选用的波数稍大于通过收敛性计算得到的临界波数,故选取n=20对纯周期声学黑洞梁进行计算;分别采用半波轴数n=20、n=40、n=50、n=110对环氧树脂-有机玻璃、铝-钢、环氧树脂-铝、环氧树脂-钢黑洞梁的前6阶带隙(即前7阶固有频率)进行计算。并且为了更好地分析带隙特性,引入归一化宽度D[18]:
(17)
式中f1、f2为带隙截止与起始频率。
3.1 纯周期声学黑洞梁
首先将利用平面波展开法计算的4种纯声学黑洞梁带隙与传递矩阵法进行对比。如图5所示,并且将2种方法计算的纯环氧树脂周期黑洞梁的具体带隙区间列入表2,从图、表可以看出,2种方法计算得出的带隙吻合良好。带隙区间、带隙宽度与归一化宽度基本一致。证明了本文利用平面波展开法计算纯周期声学黑洞梁带隙的可行性与准确性。

图5 纯周期声学黑洞梁弯曲波带隙
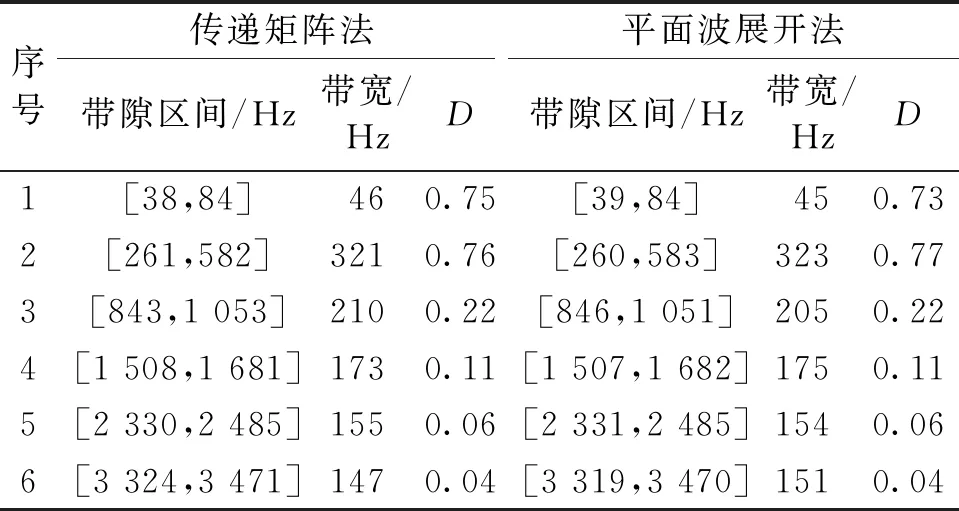
表2 传递矩阵法与平面波展开法带隙区间对比
将其余3种纯周期声学黑洞梁的具体带隙区间及带宽列入表3。结合图表可以看出,有机玻璃周期黑洞梁带隙区间最低,环氧树脂黑洞梁次之,铝与钢质声学黑洞梁带隙区间频率较高。
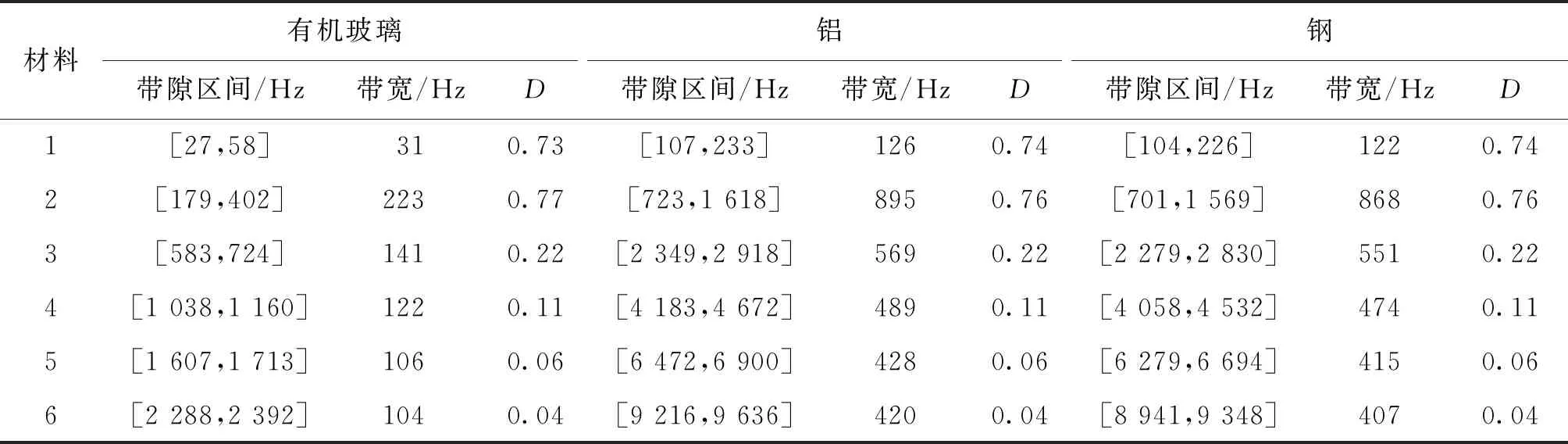
表3 不同纯周期黑洞梁带隙特性
另外,四者对应的带隙曲线变化规律一致,归一化宽度完全吻合,说明材料不同的同种结构带隙区间虽然不一致,但是可以统一用归一化宽度D去描述同种结构型式的带隙变化特性,而且前几阶带隙的归一化宽度较大,随着带隙阶数增加,归一化宽度逐渐变小,到第6阶带隙时已经衰减到很小的值,说明进行结构设计时尽量把目标频带设计到较低阶数的带隙区间内能起到更好的效果。
3.2 双材料周期声学黑洞梁
平面波展开法计算的环氧树脂-有机玻璃、铝-钢、环氧树脂-铝、环氧树脂-钢黑洞梁的前6阶带隙如图6,并将其与传递矩阵法计算的结果进行比较。从图中可以看出,平面波展开法计算的环氧树脂-有机玻璃、铝-钢周期声学黑洞梁与传递矩阵法完全一致,曲线完全重合;平面波计算的环氧树脂-铝、环氧树脂-钢黑洞梁与传递矩阵法基本吻合,计算的带隙曲线有着细微的差别,出现细微差异的原因是当材料差异较大时,即使平面波数量足够多,分解面处的材料参数展开的傅里叶级数并没有一致收敛而产生Gibbs效应[19]。但足以证明双材料周期黑洞梁带隙特性的平面波展开计算方法的正确性。
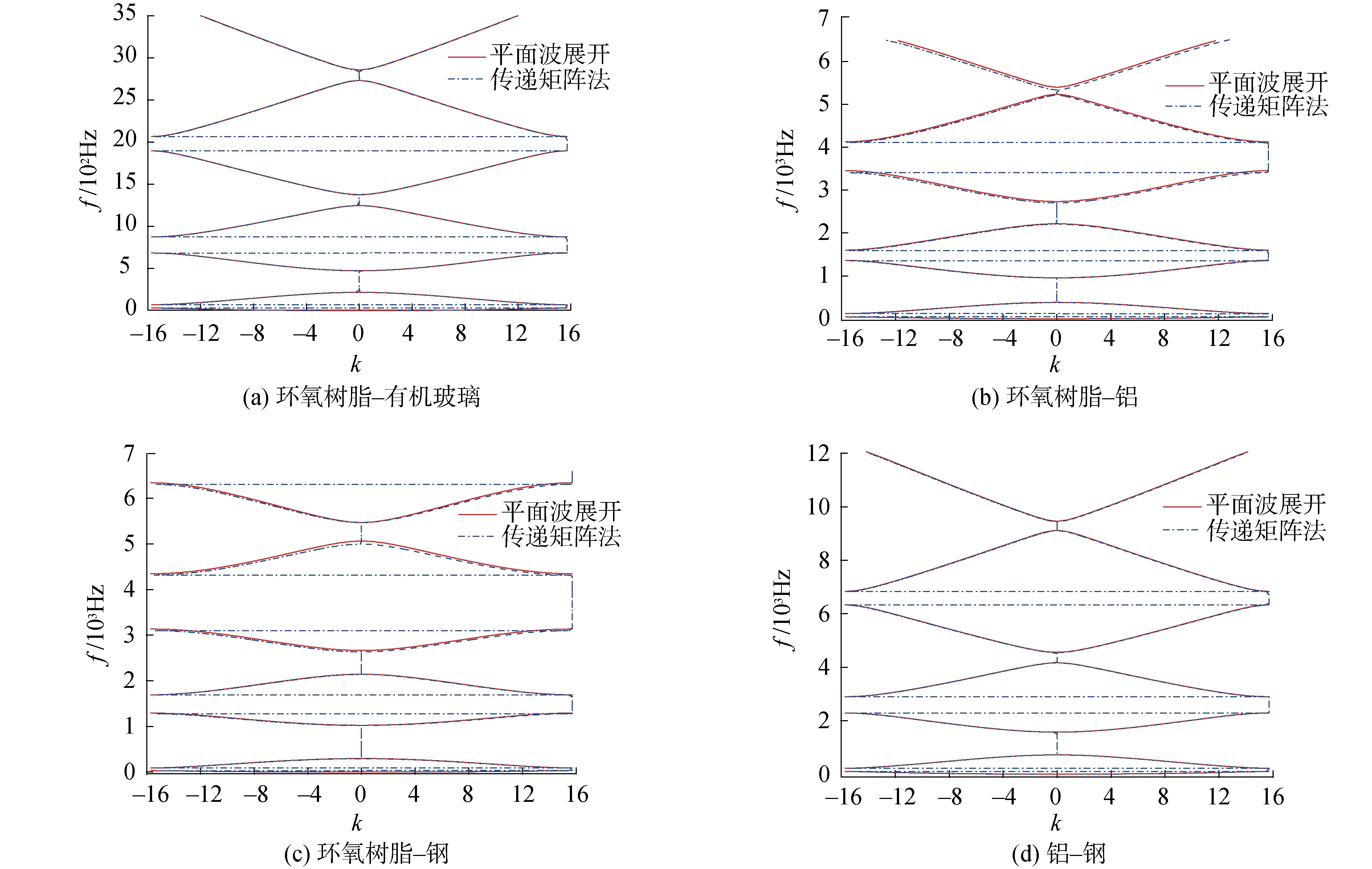
图6 双材料黑洞梁弯曲波带隙曲线
为了进一步分析材料差异对结构带隙的影响,将纯环氧树脂、环氧树脂-有机玻璃、环氧树脂-铝以及环氧树脂-钢黑洞梁的第2、5阶弯曲波带隙变化绘制在图7中。从图7中可以看出,环氧树脂与有机玻璃材料属性差异较小,因此环氧树脂-有机玻璃声学黑洞梁与环氧树脂梁弯曲波带隙差异较小,但由于有机玻璃纵波波速较小,环氧树脂-有机玻璃梁带隙起始频率与截止频率都较低。环氧树脂-钢黑洞梁的带隙起止频率较高,带隙宽度最宽,环氧树脂-铝黑洞梁次之。说明随着组成原胞的2种材料特性差异越大,带隙区间越宽,可以通过调整材料的阻抗差异获得宽频带隙。
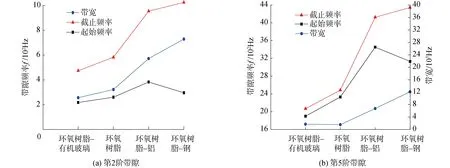
图7 不同黑洞梁带隙特性变化曲线
4 结论
1)对纯周期声学黑洞梁,结构中没有材料差异,同种结构的弯曲波带隙变化规律一致,归一化宽度保持一致,可通过归一化宽度描述同种结构的带隙特性;不同材料的纯周期黑洞结构带隙起止区间存在差异,主要取决于结构的纵波波速,波速越小,各阶带隙起始频率越低。借此可以得到更低频的带隙。
2)对2种材料构成的声学黑洞梁,结构中2种材料之间的差异会影响各阶带隙的宽度,材料之间阻抗差异越明显,各阶带隙越宽。选择不同的材料组合可以调控结构弯曲波带隙,以此获得低频宽带,为带声学黑洞结构的减振降噪提供一定思路。

