考虑水资源税下的电厂与电网之间双重边际效应模型

吴志樵， 牛宇超， 康亚玲， 唐加福

(东北财经大学 管理科学与工程学院，辽宁 大连 116025)

0 引言

国家在2002年实行了“厂网分开”电力改革[1]，上游参与方即五大发电集团会相互竞争售电给电网，而下游参与方即两大电网公司具体较强的垄断能力，逐步演化为“上游竞争、下游垄断”的结构关系。有研究表明，电厂和电网在这种电力模式下会不断追求各自利益最大化，就会造成“双重边际效应”(Double Marginalization，以下简称DM)，导致电力行业供应链效率下降[2]。

DM是供应链上下游追求自身收益最大化，在分散决策的过程中所确定的产品价格高于其边际成本，进而降低了供应链效率的现象[3]。若下游参与方产品定价过高，则会导致市场需求低迷，最终导致供应链总效益降低。据已有资料及实地调研可知，L电厂企业是某大型流域水电企业，在当地水电市场上具有举足轻重的地位，其每月平均分配电量占总电量的比例高达50%以上[4]。同时，该流域的下游电力市场均被N电网公司所占据。故本文以L电厂企业、N电网公司为研究对象，暂不研究其他参与者，N电网公司先以上网电价从L电厂购电，再给下游市场以零售价格出售。L电厂企业和N电网公司在各自决策过程中出现其目标与行业目标不一致的现象，进而导致了“双重边际效应”的产生。近年来，有资料显示煤电价格连续下滑，西南流域水电运输之后的价格相对于当地的煤电价格来说已经逐渐失去了优势，这实质上就是双重边际效应导致的[5]。在供应链研究中，下游参与方价格不变且市场随机时，库存太少是DM的一个明显特征[6]。现有研究表明，退货政策、最少数量限制等可以让零售商提升库存量[7]。此外，亦可设计契约(如收益共享合同、回购合同、数量柔性合同等)协调供应链，进而消除双重边际效应[3]。但在水利和电力领域的研究中，有关双重边际效应及其消除方式的研究很少。

近年来，水资源问题越来越成为备受关注的热点，为了提升用水效率，国家提出了水资源费改税措施，以便更好的发挥税收的调控作用。愈来愈多的省市响应国家号召，开始实行或者试点该政策[8]。目前该政策实施后的效果显著，越来越多的地区、行业均意识到这一政策的重要性。但政府部门的加入，打破了电厂和电网之间的原有博弈，此外征收水资源税也使得两者之间的DM愈加严重。

水资源现有研究大多是分析我国水资源费政策中所存在的问题[9]，并指出实施水资源费改税的重要性或者提出一些改善的对策建议[10]。另外唐升等研究多层次水资源税体系，通过数量经济模型计算每个层次的水资源税，并提出了税收方案[11]。

综上所述，现有研究未涉及电厂和电网之间的DM，同时也没有通过调控水资源税来削弱DM。供应链管理中，一般通过价格契约(price-only contract)协调各参与方。关于价格契约的研究，Lariviere等基于报童模型，将批发价格作为契约变量，描述了上下游参与方在集中决策及分散决策下的行为[6]。本文采用报童框架，纳入了水资源税这一参数变量，构建了电厂、电网的序贯博弈模型，探讨了水资源税对博弈均衡的影响，这对于通过调节税收来削弱电厂与电网之间的DM具备重要的理论意义及实用价值。

1 考虑水资源税的博弈模型

1.1 问题描述

本文涉及到的参数及变量如表1所示：

表1 参数及变量

1.2 模型分析

为便于比较，先研究“厂网分开”之前的情形，即不存在上网电价w，且并未开征水资源税，故供应链整体利润可表示为:

根据一阶条件可知，L电厂企业的售电量最优解为:

在实行“厂网分开”之后，供应链由集中决策变为分散决策。在这种情形下，L电厂先确定上网电价，N电网公司随后做出决策，即确定其购电量。通过逆序求解，可将N电网公司的利润表示为:

根据一阶条件可知，N电网公司的最优购电量为:

(1)

L电厂企业的利润可表示为:

可求得L电厂企业的最优上网电价为:

w*=ry*f(y*)+c+t

(2)

为了更好的分析，引入广义增加失效率函数g(y)，电厂的最优上网电价简化为:

(3)

定理1w*∝t,πM*∝1/t。

根据定理1，水资源税额变化正向影响电厂的最优上网电价，反向影响最优利润。以下数值实验为了进一步验证上述定理1结论。

算例1据文献[4]，设定r=0.6，c=0.01，若D满足μ=40，σ=10的正态分布。w*与t的关系图如图1(a)所示，最优利润πM*与t的关系图如图1(b)所示，验证定理1。

定理2L电厂企业利润的一阶条件为:

(4)

在定义域[0,∞)上，电厂利润函数是单峰凸函数，N电网公司的最优的购电量y*就会满足式(4)。

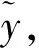
2 电力市场规模大小和需求分布的影响

2.1 电力市场规模大小

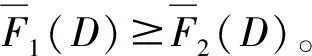
L电厂企业在更大的市场上获得的利润更大；

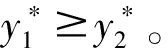
根据公式(1)及定理3假设不难发现，当售电量相同时，L电厂在市场1的售电价格更高，故利润也比市场2大。根据公式(4)及定理3的假设，当需求分布符合IGFR时，N电网在随机性大的市场上y*会更大。以下数值实验为了进一步验证定理3。

算例2根据实地调研已知，目前云南水电市场主要有“云电云用”、“云电送粤”及“云电送桂”，以下分别用市场a，b，c来表示，其中市场b在需求市场上占据很大的份额。当r=0.6，c=0.01，t=0.005时。本算例假设a，b，c需求服从[Ai,Bi]之间的均匀分布，计算出的y*及w*见表2(y*单位：亿千瓦时；w*、r、c、t单位：元/千瓦时)。

表2 计算结果表

由表2不难发现，市场c的规模及最优购电量均介于a、b之间，但最优上网电价却是三者最高。上述案例进一步验证了定理3，但案例表明，市场规模与电厂最优上网电价无关。

2.2 需求分布特性对最优上网电价的影响

由2.1节可知，电力市场规模大小不会影响电厂上网电价，还需深入分析市场需求分布特性对其的影响。

已有研究表明，若市场分布函数F满足指数分布，则需求分布函数的均值μ不会影响电厂上网电价w；假如F满足Gamma或Weibull分布，则需求分布参数的增加会引起上网电价上升[6]。以下推论1更适合一般的需求分布。

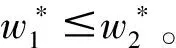
假设随机变量Xi符合μi=δi+λiμ,σi=λiσ的条件，那么由推论1可得推论2。

推论2电力市场需求不确定性CV(coefficient of variation,CV=σ/μ)正向影响电厂最优上网电价w*。

根据推论2可知，当电力市场需求不确定性较小时，即CV较小，此时电网的风险也较低，则其对购电价格也不太敏感，这种情况下L电厂会通过提高上网电价来提升自身收益，这个推论与表3.1中案例的数据相吻合。通过以下数值实验来验证w*与CV的关系。

算例3当r=0.6，c=0.01，t=0.005时，若D服从μ=1，σ最大为2的正态分布，此时w*与CV的关系图如图2(a)所示；若D服从μ=2.5，σ最大为2.5的Gamma分布，此时w*与CV的关系图如图2(b)所示。从图2中不难发现w*与CV成反比的关系，验证了推论2。

由于市场规模大小跟CV大小可以组合出四种不同的情形，下文进一步结合供应链效率来研究水资源税在何种情形下调控作用最显著。

3 供应链效率

3.1 利润的分配

“厂网分开”情形下供应链效率用πD/πI表示；电厂利润占供应链总利润比例用πM/πD表示，其中πD=πM+πR。

根据L电厂决策出w*后，可得其边际收益为w*-(c+t)=ry*f(y*)。相应的也可得到N电网边际收益为r-w*=rF(y*)。令K=y*f(y*)/F(y*)，则得到:K=(w*-c-t)/(r-w*)。

推论3当0

由于w*会随着t的变化而变化，故也无法确定t对利润分配系数K的影响。下述数值实验为了更进一步研究二者之间关系。

算例4当r=0.6，c=0.01时，若D符合μ=2，σ=1的Gamma分布，K与t的关系如图3所示。

从图3中可以看出，K随着t的下降而增大，L电厂获取超过供应链总利润的一半利润(由推论3中1

3.2 供应链效率分析

下述数值实验为了验证市场需求分布特性、水资源税额对供应链效率的影响。

算例5当r=0.6，c=0.01，t=0.005时，若D符合μ=5，σ最大为2的正态分布，关系图如图4(a)所示；若D分布符合μ=2，σ最大为2.1的Gamma分布，关系图如图4(b)所示。

由图4可知，CV随着K的增加而下降，此外当市场需求满足正态分布或者Gamma分布时，L电厂都会获得超过总利润一半的利润。而且当CV比较大的时候，L电厂获得的利润依然占据总利润的较大份额。

根据图4，πD/πI、πM/πD均随着CV的降低而上升。尽管图4(b)中电厂获得的利润比例出现小幅下降趋势，但最终的趋势是上升的，出现下降趋势是因为N电网提高售电价格所导致的。总之，不管市场需求分布符合何种分布，只要CV处于最低，那么供应链效率就会达到最高，并πM/πD明显要大于πD/πI。

当电力需求市场完全确定(即CV=0)，N电网公司失去对价格的敏感度，此时L电厂企业会不断提高电价去获取供应链总体利润。但这种情况违背了现行电力模式，且研究表明，如果供应链下游拥有机会成本时，其有更多的选择去选取获利不低于机会成本的活动[6]。本研究中上游参与方中除了L电厂外，还有其余四家大型电厂企业与其竞争，故L电厂不会不断降低CV来提高w。同时，从图4(a)中还能发现，当CV下降时，πM/πD不但高于πD/πI，并且上升速度也明显更高，故L电厂压缩N电网更有利。

第1章研究已表明，w会受t变化的影响，所以下述数值试验将验证t对供应链效率的影响。

算例6当r=0.6，c=0.01时，若D符合μ=2，σ=1的Gamma分布，t与供应链效率之间的关系如图5所示。

从图5中可以看出，随着t的下降，πM/πD和πD/πI都增加，但前者增加速度明显低于后者，这是实施水资源税而导致的。因此，进一步验证了发挥水资源税的调控作用对削弱电厂与电网之间DM的重要性。

由第2章，为分析在四种组合(市场规模大，CV大；市场规模大，CV小；市场规模小，CV大；市场规模小，CV小)下水资源税发挥的调控作用，进行下列数值实验。

算例7当r=0.6，c=0.01时，若D服从标准正态分布，市场规模大，CV大(μ=3，σ=5)、市场规模大，CV小(μ=3，σ=3)、市场规模小，CV大(μ=1，σ=5)、市场规模小，CV小(μ=1，σ=3)四种组合下，t与供应链效率之间的关系如图6(a)所示。以图6(a)中参数为标准，当σ不变，μ变为标准二倍时，t与供应链效率之间的关系如图6(b)所示；当μ不变，σ变为标准二倍时，t与供应链效率之间的关系如图6(c)所示。

根据图6不难发现，不管市场规模大小如何，只要CV较大时，供应链效率随下调t的提升速度比CV小的情形下大(图4中，CV大时供应链效率较低，且图5中供应链效率随着t的下降而升高)。同时，将图6(b)、图6(c)分别与图6(a)对比可看出，水资源税额变化对供应链效率的影响在CV增大的情形下比在市场规模增大的情形下更显著。

综上所述，不管电网面临的电力市场规模如何，只要出现市场波动较大的情形(即CV较大时)，即可建议L电厂所在地政府发挥水资源税的调控作用。

4 结论与展望

本文基于供应链模型，考虑了电厂、电网博弈主题，构建了考虑水资源税的序贯博弈模型，重点考察了水资源税对博弈均衡的作用关系及其对供应链效率的影响，得出了以下基本结论：

水资源税额正向影响电厂最优上网电价，反向影响最优利润。市场规模大小正向影响电厂的利润及电网购电量，但市场规模大小不会影响电厂的上网电价。研究表明电厂上网电价与电力市场需求不确定性成反比，电厂会提升上网电价来获得更大利润；

当需求不确定性降低时，供应链效率会得到提升，并且“厂网分开”后的供应链效率上升效果更明显，所以电厂压缩电网更有利。但“厂网分开”后，由于电网的地位提升以及各个电厂企业之间的竞争，电厂会制定一个比较低的上网电价；

电厂所在地政府可以更好的发挥税收的调控作用，下调水资源税率降低电厂最优电价，刺激购电需求，进而降低供应链损失、改善供应链整体效率，从而削弱电厂-电网双重边际效应现象。

尽管国家推行水资源费改税政策是为节约用水，提高用水效率，并且已经取得了显著的效果。但也暴露出一些问题，例如大比例加大了高耗水行业的税负；涉及水资源税征收相关部门间沟通问题；以及本文所研究的水资源税对双重边际效应的加剧问题。所以，各地政府应该规范管理高耗水行业；国家及政府部门应建立水资源税征收相关部门之间的信息共享机制[12]；同时，电厂所在地政府要发挥好水资源税的调控作用。

本研究上游参与方仅有L电厂企业，但没有考虑其余四个电厂参与竞争的情况，未来可研究存在竞争时电厂与电网之间的双重边际效应问题。同时，本研究是基于电厂与电网双方信息对称进行的，未来研究可以分析信息不对称的情况。