安全生产下政府、煤矿企业、员工的决策行为演化研究

腾 云, 刘 磊, 陈新琳, 余志刚

(1.东北农业大学 工程学院,黑龙江 哈尔滨 150030; 2.吉林大学 机械与航空航天工程学院,吉林 长春 130022; 3.东北农业大学 经济管理学院,黑龙江 哈尔滨 150030)

0 引言

安全生产事故是世界各国政府都必须面对和应对的重大问题[1,2]。进入21世纪以来，全球安全形势严峻，且因管理不善等原因直接或间接导致的重大伤亡事故频繁发生[3]。据国际劳工组织(ILO)估测，到2020年全世界劳动疾病将翻一番，发展中国家情况更为严峻[4]。中国安全科学研究院提出的“死亡弹性系数”表明，当我国GDP增长率超过5%时，每增加一个百分点，安全生产事故死亡人数随之增加2%，当GDP增长率超过7%，同步增长趋势更为明显[1]。我国安全生产事故时有发生，政府对企业有效监管是提升安全管理绩效的必要措施。

煤矿企业的特殊性、自然条件的多变性和不可预知性决定事故发生率高于其他行业，保证安全生产是煤矿企业永恒的主题[5]。我国是煤炭资源大国，也是世界第一大煤炭生产消费国，煤炭产量百万吨死亡人数平均值是波兰和南非的近30倍，美国的近100倍[6]。为避免安全生产事故的发生，我国在不断探索中发现，安全生产管理模式决定了企业安全生产状况、安全生产管理绩效以及在复杂生产状况中的企业发展力[7]。我国政府逐渐要求煤矿企业向激励型安全生产管理模式进行转化[8]。激励型安全生产管理模式是指高等水平发挥人的主动性的模式，制定以激励为主的管理制度进行安全生产管理活动[9]。

安全主动行为是提升安全生产绩效的重要因素。对生产安全事故统计发现，90%以上的安全事故都是人的不安全行为引起的。人是安全生产的主体，企业安全生产管理模式的构建应该秉承以人为中心的理念，实现被动式向主动式管理模型的跃迁[10,11]。员工安全行为与安全生产绩效密切相关，安全行为的结果变量是安全生产绩效[12～14]。现有文献表明，安全主动行为与安全事故率负相关，即安全主动性行为越多，安全事故发生率越低[15,16]。安全主动行为主要体现出了主动性与积极性，此行为是有效避免安全事故发生的重要因素。

演化博弈论是研究安全生产中多主体行为决策的有效方法。余吉安等[17]探究安全投资背后的政府和企业的利益博弈机制。Liu等建立政府、煤矿企业间动态协同博弈模型[18]。董江爱等运用博弈论分析中央政府、地方政府、煤企之间的相互博弈规律及其策略选择空间[19]；王广成等探讨了地方政府与煤炭企业在生态修复保证金制度实施中的决策演化过程[20]；毕娟等建立了基于博弈论组合赋权耦合灰靶决策的煤矿安全评价模型[21]。基于此，本研究构建出2×2×2动态演化博弈模型，揭示安全生产中政府、煤矿企业和员工决策行为的演化路径和演化规律，并找出三方行为主体决策得均衡与稳定条件。

1 假设提出与模型构建

政府相关损益为：①采取安全监管时，监管成本为C1，政府获得企业激励型模式的有利影响为D1，有利于社会稳定为W1，获得未模式转化的企业罚金为M1，给予模式转化的企业奖金为M2。②当未安全监管时，节约监控成本C1，政府获得企业激励型模式的有利影响为D1，政府承担企业惩罚型模式的不利影响为D2，对社会稳定的负面影响为W2。

煤矿企业相关损益为：①企业采取激励型模式，转化成本为C2，获得政府奖金为M2，获得员工安全主动行为的安全效益为(1-B1)L1。②若企业采取惩罚型模式，节约转化投资成本为C2，企业由于未实施模式转化而缴纳的政府罚金M1，还可获得员工安全主动行为产生的安全效益为(1-B2)L2。

员工相关损益为：政府安全监管对员工积极影响为T1，反之消极影响为T2。①在企业激励型模式下，员工安全主动行为劳动量为L1，所占安全效益比为B1，安全收益为B1L1，安全主动行为给予奖励为A1，非安全主动行为给予惩罚为A2；②在企业惩罚型模式下，员工安全主动行为劳动量为L2，员工所占安全主动行为的安全效益比为B2，员工安全收益为B2L2，惩罚型模式企业对员工非安全主动行为惩罚为A3。策略综合收益矩阵如表1所示。

表1 三方演化博弈的收益组合

2 政府、煤矿企业、员工演化博弈均衡性分析

V1X=yz(-C1+W1-M2+D1)+

y(1-z)(-C1+W1-M2+D1)+

z(1-y)(-C1+W1+M1)+

(1-y)(1-z)(-C1+W1+M1)

=-C1+W1+M1+y(-M1-M2+D1)

V2X=yz(-W2+D1+C1)+

y(1-z)(-W2+D1+C1)+

z(1-y)(-W2-D2+C1)+

(1-y)(1-z)(-W2-D2+C1)

=-W1-D2+C1+y(D1+D2)

=x[-C1+W1+M1+y(-M1-M2+D1)]+

(1-x)[-W2-D2+C1+y(D1+D2)]

V1Y=xz[-C2+M2+(1-B1)L1-A1]+

x(1-z)(-C2+M2+A2)+z(1-x)

[-C2+(1-B1)L1-A1]+

(1-x)(1-z)(-C2+A2)

=M2x+z[(1-B1)L1-A1-A2]-C2+A2

V2Y=xz[C2-M1+(1-B2)L2]+

x(1-z)(C2-M1+A3)+

z(1-x)[C2+(1-B2)L2]+

(1-x)(1-z)(C2-M1+A3)

=z[M1+(1-B2)L2-A3]+C2-M1+A3

=y[M2x+z(1-B1)L1-A1-A2-C2+A2]+

(1-y)[M1z+(1-B2)L2z-A3z+C2-M1-A3]

V1Z=xy(T1+B1L1+A1)+x(1-y)(T1+B2L2)+

y(1-x)(-T2+B1L1+A1)+

(1-x)(1-y)(-T2+B2L2)

=(T1+T2)x-T2+yB1L1+(1-y)B2L2+yA1

V2Z=xy(T1-A2)+x(1-y)(T1-A3)+

y(1-x)(-T2-A2)+(1-x)(1-y)(-T2-A3)

=(T1+T2)x-T2-A3+(A3-A2)y

=z[x(T1+T2)-T2+yB1L1+(1-y)B2L2+yA1]+

(1-z)[(T1+T2)x-T2+A3+(A3-A2)y]

2.1 政府决策复制动态分析

=x(1-x)[-2C1+W1+M1+W2+

M2+D2-y(M1+M2+D2)]

(1)

F′(x)=(1-2x)[-2C1+W1+M1+W2+

M2+D2-y(M1+M2+D2)]

(2)

2.2 煤矿决策复制动态分析

=y(1-y)[z(1-B1)L1-z(1-B2)L2-A1z-A2z+

A3z-M1z-2C2+A2+M1-A3+M2x]

(3)

=(1-2y)[z(1-B1)L1-z(1-B2)L2-A1z-A2z+

A3z-M1z-2C2+A2+M1-A3+M2x]

(4)

2.3 员工决策复制动态分析

=z(1-z)[y(A3-A2+A1)+

A3+yB1L1+(1-y)B2L2]

(5)

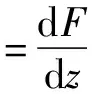
=(1-2z)[y(A2-A3+A1)+

A3+yB1L1+(1-y)B2L2]

(6)

2.4 政府、煤矿企业、员工策略演化稳定性分析

(1)政府与煤矿企业演化稳定性分析

由(1)和(3)式可知政府和煤矿企业动态博弈含有5个均衡点当且仅当

Jacobi矩阵:

detJ1=(1-2x)[-2C1+W1+M1+W2+M2+D2-y(M1+M2+D2)]

(1-2y)[z(1-B1)L1-z(1-B2)L2-A1z-A2z+A3z-M1z-2C2+A2+M1-A3+M2x]-

x(1-x)(M1+M2+D2)y(1-y)M2

trJ1=(1-2x)[-2C1+W1+M1+W2+M2+D2-y(M1+M2+D2)]+

(1-2y)[z(1-B1)L1-z(1-B2)L2-A1z-A2z+A3z-M1z-2C2+A2+M1-A3+M2x]

稳定性分析结果见表2。

表2 政府、煤矿企业演化博弈稳定性结果分析

(2)煤矿企业与员工演化稳定性分析

Jacobi矩阵:

detJ1=(1-2y)[z(1-B1)L1-z(1-B2)L2-A1z-A2z+A3z-M1z-2C2+A2+M1-A3+M2x]·

(1-2z)[y(A2-A3+A1)+A3+yB1L1+(1-y)B2L2]

y(1-y)[(1-B1)L1-(1-B2)-A1-A2+A3-M1]z(1-z)(B1L1-B2L2+A3-A2+A1)

trJ2=(1-2y)[z(1-B1)L1-z(1-B2)L2-A1z-A2z+A3z-M1z-2C2+A2+M1-A3+M2x]+

(1-2z)[y(A2-A3+A1)+A3+yB1L1+(1-y)B2L2]

稳定性分析结果见表3。

表3 煤矿企业、员工演化博弈稳定性分析结果

3 数值实验和仿真

本研究三方博弈最终演化为理想状态x=1,y=1,z=1。运用Matlab软件进行数值仿真，设置参数值为：D1=15，D2=20，W1=50，W2=40，B1=0.7，B2=0.3，L1=10，L2=5，T1=20，T2=25，C1=40，C2=10，M1=40，M2=35，A2=10，A1=20，A3=25。以x0=0.4，y0=0.6，z0=0.5为例。

政府对企业惩罚与奖励对演化过程的影响。取值为M1=15，M2=15；M1=50，M2=50；M1=15，M2=50；M1=50，M2=15。从图1中得出，当惩罚固定且奖励增加、奖励固定且惩罚增加、奖励大于惩罚时，三方收敛到理想状态的时间减少。当奖励小于惩罚时，三方收敛到理想状态的时间增加。当奖励与惩罚均大时，三方收敛到理想状态的时间最短。

激励型企业给予员工行为的奖励与惩罚对演化过程的影响。取值为A1=10，A2=10；A1=30，A2=30；A1=10，A2=50；A1=50，A2=10。从图2中得出，当奖励小于惩罚时，三方收敛到理想状态的时间增加。当奖励大于惩罚时，三方收敛到理想状态的时间减少。当奖励与惩罚均大时，三方收敛到理想状态的时间最少。

政府监管成本变化对演化过程的影响。C1值取5，20，40，70。从图3中得出，当政府监管成本增加，三方收敛到理想状态的时间减少。但政府监管成本增大超过范围，演化路径改变较大，出现螺旋演化路径，无法趋向理想状态。

企业模式转化成本变化对演化过程的影响。C2值分别取5，20，40，70。从图4中得出，当转化成本增加时，三方决策收敛的速度减慢。但企业转化成本逐渐增大超过一定范围，演化路径发生较大改变，无法趋向理想状态。

惩罚型企业对员工惩罚对演化过程的影响。A3值取0，20，40，70。从图5中得出，当惩罚为零或者过大时，虽然三方演化结果为理想状态，但是收敛速度较慢，后者与前者相比，收敛速度快。当惩罚在适中范围内，随着惩罚增加，三方最终演化为理想状态。

4 结论和对策建议

4.1 研究结论

从决策复制动态方程可知，政府决策会直接受到企业决策的影响，而不会受到员工决策的影响；煤矿企业决策均受到企业决策和员工决策两者的影响；员工决策均受到政府决策和企业决策影响。政府、企业、员工三方决策的桥梁是企业，在安全生产管理过程中，需要明确三者之间的影响关系。

从演化稳定性分析可知，企业与员工之间存在任何条件都无法达到稳定状态的策略。三方达到理想状态需要同时满足三个条件：当企业采取激励型获得政府给予奖金的期望小于企业模式转化成本与企业鼓励员工安全主动行为额外奖励之和；当政府进行管与不进行安全监管对社会稳定带来的影响之和小于政府投入成本的2倍；企业由于未实施模式转化而缴纳给政府罚金与期望之和小于企业采取激励型模式转化成本。

从数值仿真结果可知，三者向理想状态演化过程表现为：政府采取轻奖轻罚、重罚轻奖、轻罚重奖、重奖重罚四种奖惩模式，三方收敛到理想状态时间逐渐变短；激励型企业重奖轻罚时，三方收敛到理想状态时间较少；当重奖重罚时，三方收敛到理想状态速度最快；府投入监管成本在一定范围内增加，三方收敛到理想状态时间减少；④企业激励型转化成本逐渐增加时，三方收敛到理想状态时间增加。但转化成本超过一定范围，无法趋向理想状态。⑤惩罚型模式企业对员工惩罚力度过大或过小，三方收敛到理想状态所需要时间减少。

4.2 建议和展望

政府是企业安全生产强有力的推动者，鼓励多部门分工协作，落实综合安全管理，强调安全管理的综合性和多层面性。政府监管部门可以适当降低安全监管成本和加大惩罚力度，财政部门提供企业经济支撑，促使企业实现惩罚型向激励型安全生产管理模式的跃迁。应该构建政府、市场、社会多主体驱动机制，促使煤矿企业将安全生产管理模式提升的目标内在化、自主化。

煤矿企业作为三方博弈的中间者，应该积极响应政府和充分调动员工积极性，实现惩罚型向激励型安全生产管理模式的跃迁。惩罚型安全生产管理模式导致员工安全意识不足、安全知识缺乏、安全防护不到位，对企业安全生产绩效产生消极影响。激励型安全生产管理模式重视员工心理因素，通过各种适当激励手段引导员工的安全意识、观念、态度，增加员工安全主动行为，对企业安全生产绩效产生积极影响。

员工是安全生产直接影响因素，员工不安全行为是导致安全事故的主要因素之一，企业构建合理的安全生产管理模式有利于激发员工安全主动行为。企业应该遵循引导人的行为的管理理念、运用各种手段和措施调动人的主动性行为的管理方法、制定以激励为主的管理制度，充分发挥员工的主人翁精神，使员工主动参与到安全生产中，实现“要我安全”向“我要安全”的思想转化。

本研究揭示安全生产中政府、煤矿企业和员工决策行为的演化路径和演化规律，以及找出主体决策达到理想状态的均衡和稳定条件，并进行数值仿真验证，为安全生产提供理论借鉴和实践指导。未来研究重点是要收集实际调研数据，进一步仿真研究，使研究结论更加客观性、科学性。