基于自抗扰控制的永磁同步电机伺服控制系统*

王志达 韩 亮 丁胜夺

（中国石油集团安全环保技术研究院有限公司HSE信息中心 北京 102206）

1 引言

永磁同步电机因其效率高、扭矩大、使用寿命长而越来越受到人们的青睐［1］，但在实际应用中，其结构和控制电路性能的影响制约了永磁同步电机的发展，而良好的控制系统可以显著提升其性能［2］，因此，电机控制系统的设计具有重要意义。

在电机控制系统中，伺服控制占有重要地位［3］。最初广泛采用PID 控制实现电机伺服控制，该控制方法具有结构简单，运算量小，鲁棒性强等优点，因此被广泛应用于对控制精度和响应速度不高的控制领域中［4～10］。在后来的研究中提出了以现代控制理论为基础的控制方法，如滑模变结构控制［11～18］，自适应控制［19～20］等，增加了控制的精度，但存在抖动、系统开销大、难以满足伺服控制系统快速响应要求的问题。随着人工智能技术的发展，研究人员提出智能控制方法，该方法不依赖或不完全依赖被控对象的数学模型，而是以实际的控制效果为指标进行控制，能够充分考虑到系统的不确定性，如模糊控制、神经网络控制［21～24］等，但目前存在依赖经验、专家知识、数据使得控制精度难以保证的情况。

自抗扰控制器（ADRC）具有结构明晰、算法简单、响应速度快、控制精度高，对受控对象模型的不确定性因素和外扰具有优良的适应性和鲁棒性的特点［25～26］，能够准确地实时估计系统的总扰动，对于系统内部干扰和外部干扰，随机干扰和固定的干扰都具有很好的估计效果，将估计的扰动值补偿给闭环系统的输入，把一个复杂的系统变换成为一个简单的线性系统，从而使闭环系统获得良好的控制性能，可有效提高伺服控制系统的性能［27］。

2 数学模型

2.1 控制系统结构

基于自抗扰控制的永磁同步电机伺服控制系统如图1 所示。该控制系统包含位置环控制器、电流环控制器以及磁场定向控制（FOC）部分，其中位置环采用自抗扰控制，包含微分跟踪器、非线性组合以及扩张状态观测器。微分跟踪器为参考输入安排过渡过程并提供高信噪比的微分信号，提高了系统的稳定性，扩张状态观测器可以用来跟踪系统各状态变量并估计出系统模型的不确定因素和干扰的实时值，线性反馈控制律通过误差及误差的微分的组合产生需要的电流值［25～26］。电流环采用PI控制。FOC 部分包含Park 逆变换、SVPWM、Park 变换以及Clarke变换。该控制结构鲁棒性强，可有效提高伺服控制的精度。

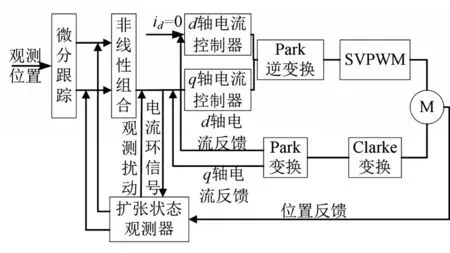
图1 伺服控制系统结构

2.2 永磁同步电机数学模型

永磁同步电机的定子采用三相对称绕组，转子为永磁体，定转子通过气隙磁场相互作用，存在电磁耦合关系。永磁同步电机在d-q 轴坐标系下的数学模型如下［1］：

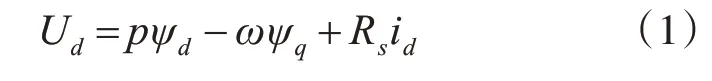
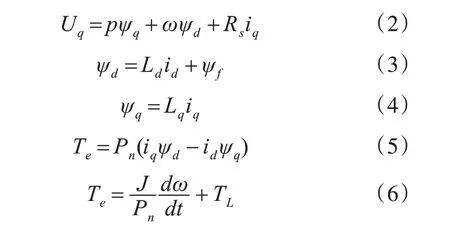
式中，ψd、ψq为d、q 轴磁链，Rs为定子电阻，id、iq为d、q 轴电流，Ld、Lq为d、q 轴电感，ψf转子磁钢在定子上的耦合磁链，Te为电磁转矩，Pn为极对数，TL为负载转矩，J为转动惯量。

由式（1）～（6）可得电磁转矩的另一表达式：

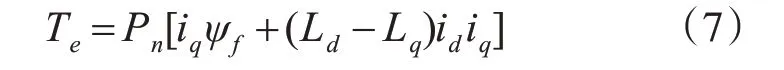
2.3 位置环控制器

ADRC 控制器包括微分跟踪器，扩张状态跟踪器，和线性反馈控制律，针对伺服控制系统，微分跟踪器表达式如下：

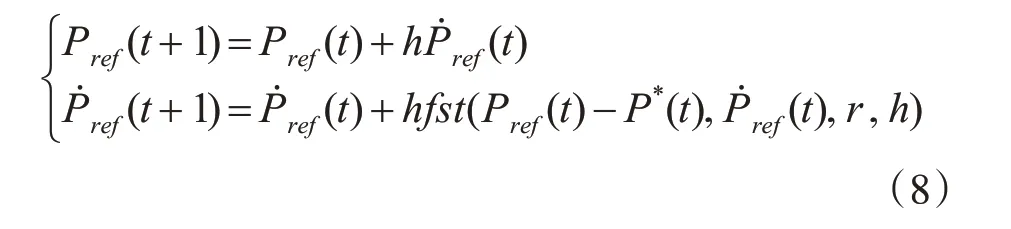
式中，Pref为电机参考位置，P˙ref为电机参考位置信号的微分，即电机的转速，r，h 为系统待调参数，fst为快速控制最优综合函数。

扩张状态观测器用来获取测量转速信号的跟踪值及其微分信号，其表达式如下：

式中，x1为测量电机位置的跟踪信号，P 为测量转速信号，x2为测量电机位置的微分信号，即观测的电机转速，w为扰动的跟踪信号，u 为输入电机的参考电流值，β01、β02、β03、b、a1、a2为系统的待调参数，fal为系统函数。

线性反馈控制律通过误差及误差的微分的组合产生需要的电流值iref，表达式如下：

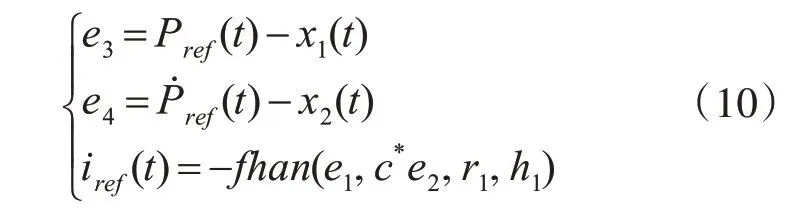
式中，e3为位置的误差值，e4为转速的误差值。

3 仿真分析

本节利用Matlab/Simulink 平台进行仿真，仿真所用电机参数如表1所示，仿真模型如图2所示，模拟时采用ode23tb 算法，模拟时间为10s，最大时间步长0.00125s，分别分析不同负载转矩及系统扰动条件下的控制误差。

表1 仿真用永磁同步电机参数

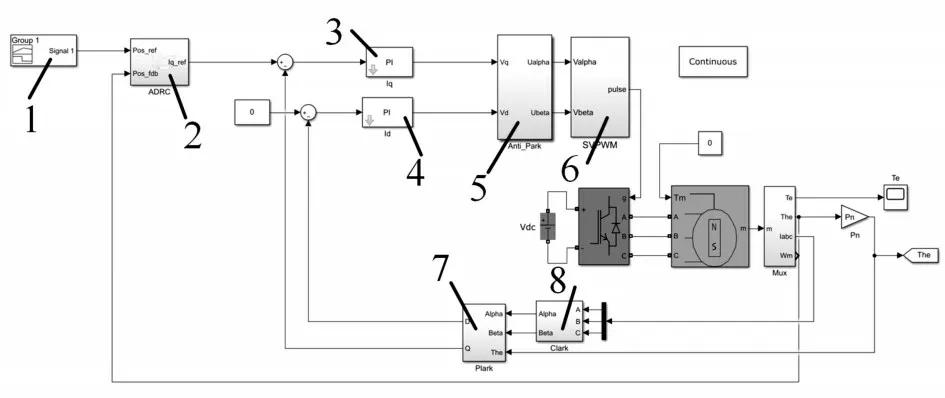
图2 伺服控制系统仿真模型

ADRC控制器的仿真模型如图3所示。该控制模型包含微分跟踪器（TD），非线性组合（NonLC）和扩张状态观测器（ESO）三部分，三部分均采用S 函数搭建。位置参考信号经微分跟踪器平滑后与扩张状态观测器观测值比较产生偏差信号，该偏差信号经非线性组合运算后与扩张状态观测器观测出的扰动信号叠加得到q轴电流参考信号。

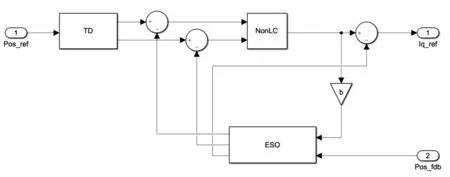
图3 ADRC控制器仿真模型

阶跃负载转矩影响下电机伺服误差如图4 所示，伺服跟踪控制效果如图5 所示。仿真时负载转矩为阶跃式，初始幅值为0，阶跃后幅值为2N·m，在5s 时产生幅值阶跃。由图可以看出，伺服跟踪控制效果较好，曲线无明显超调。当电机空载转动控制偏差随转速的增加逐渐增大，2s～4s 电机匀速运动，控制偏差保持在0.13°，4s 后电机减速运动，控制偏差逐渐减小，突然施加负载转矩时，控制偏差并未产生明显变化，控制偏差最小值为0.11°。随后电机带载运动，控制偏差变化规律与空载时相同，并未明显受负载转矩影响，由此可以看出，该位置控制系统鲁棒性较强，可有效抵抗阶跃型负载转矩的影响。

图4 阶跃负载转矩下电机伺服误差

图5 阶跃负载转矩下电机转角变化

阶跃负载转矩条件下电机转速变化情况如图6 所示。由图可以看出，伺服控制时电机转速与规划转速几乎一致，且电机转速波动较小，波动最大值为100rpm。在电机启动阶段，电机转速与规划转速偏差较小，阶跃载荷几乎对电机转速无影响，当电机带载运动时，由于负载转矩的影响，电机转速波动略微增加。

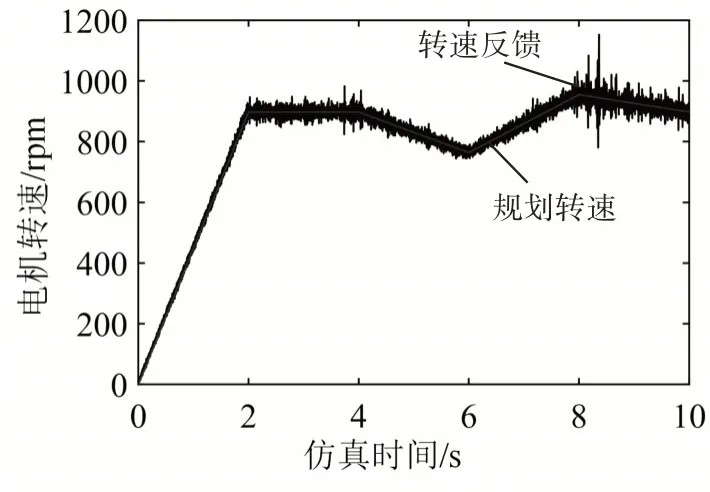
图6 阶跃负载转矩下电机转速变化

交变负载转矩与系统扰动作用下电机伺服误差如图7所示，控制效果如图8所示，其中交变负载转矩为幅值为3N·m，周期为1s 的正弦信号，系统扰动为随机信号。由图可以看出，交变负载转矩与系统扰动对该控制系统影响很小。位置误差随电机转速的增加逐渐增大，在2s 以后，交变负载转矩与系统扰动对于控制系统具有轻微影响，位置误差最大值为0.13°，最小值为0.11°。通过与图4、图5对比可以看出，位置偏差几乎未发生变化，由此可以说明该控制系统具有较强的鲁棒性。

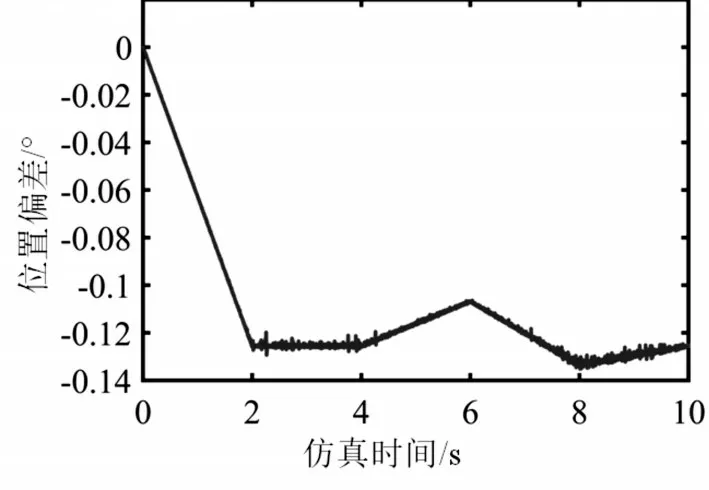
图7 交变负载转矩与系统扰动作用下伺服控制误差

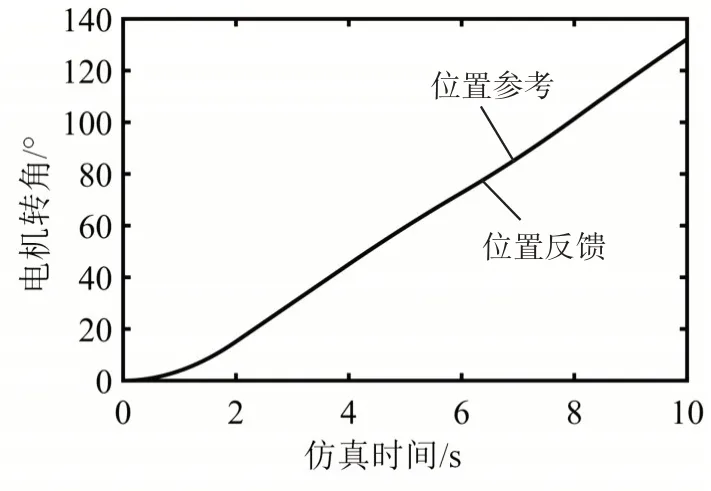
图8 交变负载转矩与系统扰动作用下电机伺服效果

交变负载转矩与系统扰动作用下电机转速变化如图9 所示。由图可以看出，交变负载转矩与系统扰动主要影响2s 以后电机的转速，但电机的转速变化与规划值几乎一致。对比图6 可以看出，交变负载转矩与系统扰动对系统的影响更大，该控制系统具备较强的鲁棒性，且可自动补偿系统扰动。

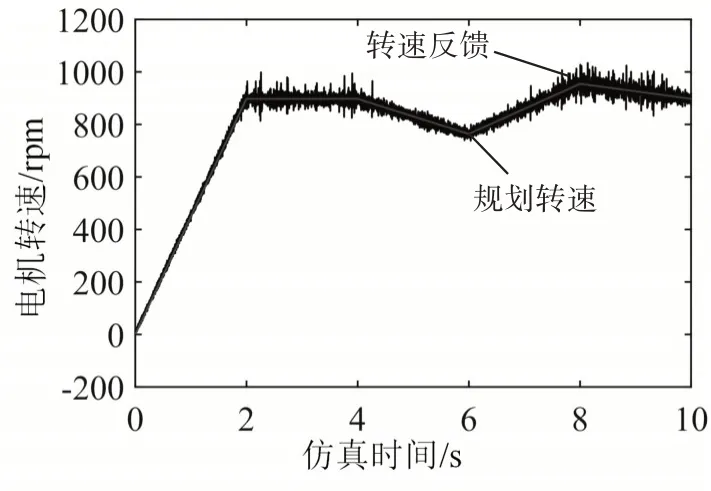
图9 交变负载转矩与系统扰动作用下电机转速

4 实验

随后采用实验验证该控制系统的性能。实验时采用实验仪器如图10 所示，其中旋变用于测量电机的位置，控制板用于生成控制信号，驱动板用于驱动电机转动，上位机通过CAN 卡与下位机通信。负载转矩近似呈正弦规律变化，幅值为3.5N·m，与模拟时采用的负载转矩较为吻合，如图11 所示。

图10 实验平台

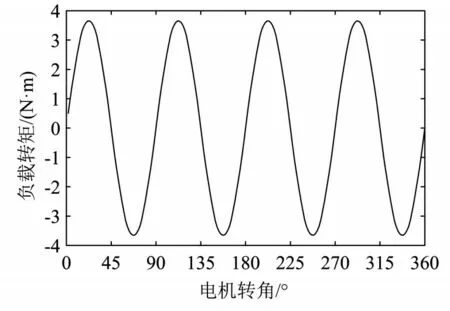
图11 负载转矩特性

实验结果如图12 所示。由图12（a）和（b）可以看出，在交变负载转矩下，电机位置误差呈交变状态，最大为0.6°。电流环控制误差变化剧烈，变化范围为-0.4A～0.3A，这是由于负载转矩呈交变状态，控制时为适应负载转矩，电机电流不断变化，使得电机的转速不稳定，进而导致位置偏差剧烈波动。由此可以看出，该控制系统的鲁棒性较好，在交变负载转矩下仍可保持较高的控制精度。

5 结语

本文以设计强鲁棒性伺服控制系统为目标，基于自抗扰控制理论，提出基于自抗扰控制的永磁同步电机伺服控制系统，并采用仿真验证控制系统的性能，得到如下结论。

1）电机空载运动时，控制误差随电机转速增加而增大，最大值为0.13°，阶跃负载对控制系统几乎无影响，在恒定负载转矩作用下控制误差最小值为0.11°。电机转速与规划转速几乎一致。

2）交变负载转矩与系统扰动作用下电机控制误差最大值为0.13°，最小值为0.11°，与空载情况几乎相同，电机转速未发生明显变化，由此可以看出，该控制系统具有较强的鲁棒性。

3）实验表明在幅值为3.5N·m 的交变负载转矩下电机位置误差呈交变状态，最大为0.6°。电流环控制误差变化剧烈，变化范围为-0.4A～0.3A，该控制系统具有较强的鲁棒性。