寻找矩阵最大线性无关子块的两种算法研究

王 芳，马艳丽

(1.安徽外国语学院 信息与数学学院，安徽 合肥 231200；2.安徽新华学院 通识教育部，安徽合肥 230088)

1 相关定义及引理

定义1[1]若矩阵A∈Rm×n的秩为r，则A必有一个非奇异的子矩阵A11∈Rr×r，称A11为矩阵A的最大线性无关子块。

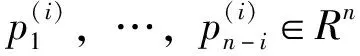
引理2[3]r维向量组的每一个向量添加n-r个分量成为n维向量。如果r维向量组线性无关，那么，n维向量组也线性无关。反言之，如果n维向量组线性相关，那么，r维向量组也线性相关。

2 寻找矩阵中最大线性无关子块的两种算法

由引理2可知对于n维向量组，判断线性相关性，只需判断n维向量组中的每一个向量去掉n-r个分量后所形成的r维向量组的线性相关性即可。因为r+1个r维向量组一定线性相关，故在实际应用中需考虑向量组中向量的个数。

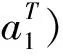
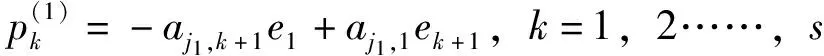
(1)

其中

(2)

求出齐次线性方程组Λsx=0的一个基础解系。其中

Λs=(h1,h2,h3,…hs)T

(3)

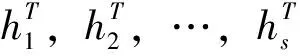
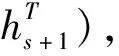
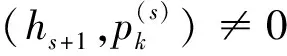
③矩阵B是一个行满秩矩阵，行向量的先后顺序与矩阵A中的有区别。而若已知矩阵A∈Rm×n，PA=B，其中矩阵B∈Rr×n的秩为r，P∈Rr×m是某置换矩阵的前r行，在MATLAB中输入以下命令

B=P′*B;B(all(B==0,2),∶)=[]

可使B的行向量的先后顺序与在矩阵A中的先后顺序相等。

具体算法如下：

算法1

1)令size(A)=[m,n]，置初始量：m阶单位矩阵Im×m，u=2，v=1，k=2，r=2,l=1,P、B为空矩阵，分别将矩阵Im×m和A的第一行移动到矩阵P、B的第一行。

2)当u小于等于n，令l1=1，取u阶单位矩阵Iu×u，p(∶,u-1)=-a(u)×Iu×u(∶,1)+a(1)×Iu×u(∶,u)。若l1小于等于m-1，c=max(|A(l1,1∶u)×p|),如果c大于给定的ε，v增加1，并分别将矩阵Im×m和A的第l1行移动到矩阵P、B的第v行。停止,l1增加1，如果l1大于m-1，u增加1，p(u,u-1)=0，c大于给定的ε，停止。

3)对t=u+1,……,n，取t阶单位矩阵It×t，令p(t,t-1)=0，p(∶,t-1)=-a(t)×It×t(∶,1)+a(1)×It×t(∶,t),b=p,r=2;当r小于等于v，取空矩阵Q，计算B(r,1:t)×b，并将其值赋予矩阵Q，令[c,i]=max{|Q|}，用g表示矩阵b的第i列。

对于j=1,2,……，t-r+1，计算b(∶,j)=b(∶,j)-Q(j)×g/Q(i)，去掉矩阵b的第i列，r增加1。

令size(A)=[m1,n1]，l=1。

若k小于等于t，l大于m1，取空矩阵Q，计算A(l,1∶t)×b，并将其值赋予矩阵Q，令[c,i]=max{|Q|}，用g表示矩阵b的第i列。

如果c大于给定的ε，v增加1，并分别将矩阵Im×m和A的第l行移动到矩阵P、B的第v行，l减小1，m1减小1，令size(b)=[m2,n2]，n2-1小于等于0，停止运行。

对j=1,……n2，计算b(∶,j)=b(∶,j)-Q(j)×g/Q(i)，去掉矩阵b的第i列，k增加1，终止，l增加1。

如果v-m大于等于零(B的行数大于等于A的行数)，程序终止。

如果v-t大于等于零(B的行数大于等于A的列数)，程序终止。

t增加1，令B=PTB，去掉B中的全零行；输出B。

算法1所得到的矩阵B为行满秩矩阵，它的行向量组是矩阵A的行向量组的一个极大线性无关组，假设size(B)=(r,n)，r即为矩阵A的秩，然后对BT采用算法1，再取转置，即可得到最大线性无关子块A11。显然A11所对应的行列式即为矩阵的最高阶非零子式，若已知道rank(A)，则找到rank(A)维线性无关子块即可中断。

以上算法是先提取矩阵A的行向量组的一个极大线性无关组，然后形成最大线性无关子块，接下来将考虑直接寻找最大线性无关子块的算法，其主要思想是从二维最大线性无关子块开始，已知r维线性无关块(不一定是矩阵A的子式)，然后在其基础上寻找r+1阶线性无关块。主要方法是在r的每一个行向量添加一个分量，形成含有r个r+1维向量的线性无关组，然后利用引理1寻找第r+1个r+1维向量，使其与已寻找到的r个r+1维向量线性无关，如果不存在，则互换矩阵A的两列，并重新添加一个分量，重新寻找，直到找遍所有行与列即可停止，若已知rank(A)，则找到rank(A)维线性无关子块即可中断。

若已知矩阵A∈Rm×n且MAN=B，M、N是置换矩阵，B的秩为r,B的前r行、前r列构成B的最大线性无关子块，则A的最大线性无关子块可通过在MATLAB中输入以下命令得到：M(r+1∶m,∶)=0,M=MT;N(∶,r+1∶n)=0;N=NT;B=M*A*N;B(all(B==0,2),∶)=[];B(∶,all(B==0,1))=[]。

直接提取最大线性无关子块的具体算法如下：

算法2

1)取初始量：m阶单位矩阵Im×n,n阶单位矩阵In×n，u=2，k1=0，hh=0，令v=min(m,n)。

2)若u小于等于v，取矩阵A第一行的前u列，u阶单位矩阵In×n，令

p(∶,u-1)=-a(u)×Iu×u(∶,1)+a(1)×Iu×u(∶,u)，b=p,r=2。

若r小于等于u-1，取空矩阵G，计算A(r,1∶u)×b，并将其值赋予矩阵G，令[c,i]=max{|G|}，用g表示矩阵b的第i列。

对于j=1,2,……,u-r+1，计算b(∶,j)=b(∶,j)-G(j)×g/G(i)，去掉矩阵b的第i列，r增加,程序终止。

l=u，当l小于等于m，令c=max(|A(l,1∶u)×b|)。

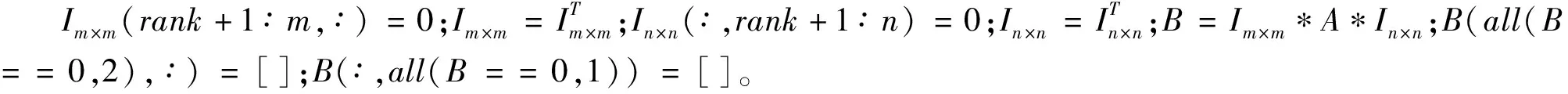
算法2输出的矩阵B就是矩阵A的最大线性无关子块A11。

3 数值实验

以下数值实验均在Intel(R)Core(TM)i5-8265U CPU @ 1.60 GHz 1.80 GHz内存为8.00 GB的个人计算机上完成，所用软件为MATLAB R2018a[4-6]。

方法1：

在MATLAB命令窗口输入矩阵A=[1-1 2 1 0;2-2 4 2 0;3 0 6-1 1;0 3 0 0 1]，使用算法1可得行满秩矩阵B：

令B=BT,对B使用算法1并取转置可得：

方法2：

在MATLAB命令窗口输入矩阵A=[1-1 2 1 0;2-2 4 2 0;3 0 6-1 1;0 3 0 0 1]，直接使用算法2即可得最大线性无关子块：

数值实验2使用算法1、算法2提取矩阵(表1)，矩阵来自“Matrix Market”，皆为实数矩阵的最大线性无关子块，其中ε取1.1×10-10，ti(i=1,2)依次表示两种算法的CPU运行时间(单位为s)。

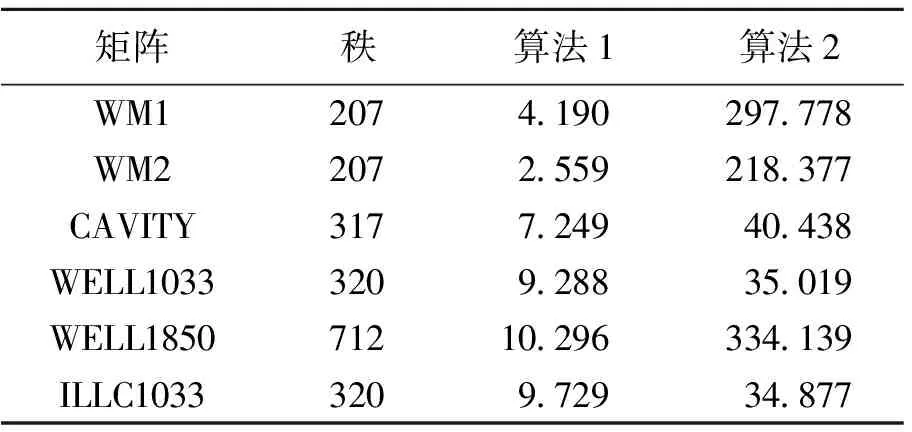
表1 两种算法的运行时间 s

4 结论与讨论

两种算法虽可用来提取大型稀疏矩阵的最大线性无关子块，但时间上并不占优势。所需CPU运行时间第一种算法远远比第二种算法短，两种算法CPU运行时间与矩阵内部的线性关系有很大联系。两种算法可清楚地看到矩阵内部的线性无关性，即矩阵的行与列的局部线性无关性。另外如果需要求取矩阵的秩及提取最大线性无关子块时的置换矩阵，只需输出时稍作改动即可。

我们在使用基于恰当分裂的预条件QMR算法和预条件GMRES算法[7-10]求解奇异线性方程组时，可使用这两种算法提取最大线性无关子块和置换矩阵来构造预条件子。