基于一致分布佳点集改进的交叉人工蜂群算法
张平华,贾万祥,程晓蕾
(1.合肥职业技术学院,安徽 合肥 230000;2.万博科技职业学院,安徽 合肥 230000)
近年来,国内外的研究学者对基于智能优化规则的启发式算法做了大量的研究,各种不同的先进智能的仿生群智能算法不断出现(如鱼群算法、蛙跳算法、禁忌搜索算法、遗传算法、蚁群算法、粒子群算法等),并被逐步应用到组合优化和资源高度等各方面的问题求解中。仿生群智能是指众多简单的个体通过相互协同方式,表现出复杂的智能行为的过程和特性。群体智能算法主要有模拟蚂蚁觅食行为的蚁群算法[1](ant colony optimization,ACO)、源于鸟群觅食行为的粒子群算法[2](particle swarm optimization,PSO)、模拟真实鱼类觅食行为的人工鱼群算法[3](artificial fish swarm algorithm,AFSA)、模拟自然界中萤火虫成虫发光的生物学特性的萤火虫算法[4](glowworm swarm optimization,GSO)以及模拟蜜蜂群体寻找优良蜜源的人工蜂群算法(artificial bee colony,ABC)[5]等。
人工蜂群算法[6]是由土耳其Erciyes大学的Karaboga教授在美国Virginia Tech大学的Teodorovic的蜂群优化(bee colony optimization,BCO)和英国Cambridge大学的Yang等的一种虚拟蜜蜂(virtual bee algorithm,VBA)算法的研究基础上,于2005年在一份内部技术报告中系统地提出的一种新型群智能优化算法。在组合优化方面已经被证实比上述的智能算法具有更优越的性能[7]。G.Zhu和S.Kwong[8]优化了蜜源产生位置的规则,在ABC算法中引入全局最优,提高了算法的开发能力;王伟[9]将遗传算法的交叉算子引入了ABC算法中,提出了一种基于交叉算子的改进人工蜂群算法(MABC),提高了算法的局部搜索能力,加快了收敛速度;在DE算法的变异策略启发下,W.Gao[10]等通过产生候选蜜源位置,改进了蜂群对蜜源的搜索能力,提出了CABC算法;刘三阳[11]等引入局部搜索算子,利用随机局部搜索算子对当前最优进行局部搜索,以加快算法的收敛速度;B.Akay[12]等通过控制扰动频率来加快算法的收敛速度。
针对算法后期收敛速度慢、易于陷入局部极值的问题,结合数论和交叉方法提出了一种基于一致分布佳点集改进的交叉人工蜂群算法。通过一致分布佳点集对算法种群的初始化进行改进,以维持种群的均匀分布和多样性,提高了收敛速度及精度;在全局最优的基础上引入交叉系数,通过交叉方式进行迭代更新位置,增强全局寻优能力,有效地避免算法陷入局部最优,提高优化能力。
1 人工蜂群算法及计算框架
1.1 人工蜂群算法概述
依据文献[6]中的描述,ABC算法主要由4个基本组成元素:食物源(蜜源,food source)、引领蜂(又称采蜜蜂或雇佣蜂,employed forager,EF)、跟随蜂(又称观察蜂onlooker,或非雇佣蜂unemployed forager,UF)、侦察蜂(scout)。其中引领蜂和跟随蜂用来开采蜜源,即寻找最优解,而侦查蜂用来观察是否陷入局部最优[13];两种基本的智能行为模式:(1)招募行为(recruit):采蜜蜂在蜂巢跳舞区传递蜜源信息,招募待工蜂(观察蜂);(2)放弃(abandon)行为:某个食物源被持续开采极限(limit)次后,采蜜蜂放弃该蜜源成为侦察蜂。
1.2 ABC算法框架描述
根据求解组合优化问题的分析,可以建立ABC算法的进行求解智能优化问题的数学模型:
minf(x);x=(x1,x2,…,xD)∈G
(1)
其中,D是优化问题的维数,f(x)为优化的目标函数,G为可行解的解空间(可以用上下界来表示,如[lb,ub])。
在ABC算法中,蜜源亦即优化问题的解,通常用一个N维向量来表示;蜜源的优劣用优化函数的适应度值来衡量。算法框架描述如下。
1.2.1 初始化(initialization)阶段
初始化人工蜂群的规模(SN)、最大迭代次数(maxCycle)、最大开采次数(limit);初始化SN/2个D维的可行解Xi=(Xi1,Xi2,…,XiD)T(i=1,2,…,SN):
(2)
1.2.2 引领蜂阶段
引领蜂依据(2)式进行领域搜索,并采用贪婪算法或轮盘赌算法依据(3)式计算初始适应度值(fitness(xi)),并按(4)式求出对蜜源选择的概率(pi):
(3)
其中,f(xi)为待优化的函数,fitness(xi)为函数的适应度值。
1.2.3 跟随蜂阶段
跟随蜂依据(3)式计算跟随概率,搜索蜜源,并计算适应度值,选择相关蜜源。
(4)
1.2.4 侦察蜂阶段
侦察蜂在其领域范围内随机地搜索新的蜜源。当蜜源经过限定的最大开采次数后,如果仍然没有改进,则在此采蜜的引领蜂就放弃此蜜源,并变为侦查蜂,从而重新按(2)式随机选取新的蜜源,产生新蜜源位置。
2 改进的人工蜂群算法
人工蜂群算法求解问题时,主要利用种群的智能迭代搜索解空间,对食物源初始化采用随机分布方式,这可能导致部分初始解过于集中或重合,经多次实验证明种群的初始化的程序影响着算法的收敛速度和解的质量。随机点分布如图1所示。
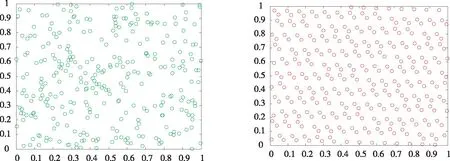
图1 二维随机点分布 图2 一致均匀佳点分布
2.1 基于佳点集的种群初始化
对一个未知的分布,采用随机方法(RAND)取点法时,偏差一般是O(n(1-/2)),由华罗庚等在文献[14]中提出的具有“最佳一致分布的佳点集”的方法取点时,其偏差仅为O(n(-1+ε)),两者相差102倍。由此可见,用佳点集方法比随机方法偏差要小得多。即在相同取点个数的条件下,一致分布的佳点集序列要比随机方法方式选取的点序列更均匀。若将S维欧式空间中的单位立方体GS上的佳点映射到求解空间,可以构造出一个均匀取点方法,如图2所示。
张铃教授利用佳点集法选择点比随机选取点的偏差要小得多等理论对遗传算法进行了改进,在算法的收敛性和解的精度方面均取得了非常优越的效果。佳点的分布,不管取多少点多少次,其分布情况每次都是一致均匀的,而其他分布形式则不能达到这样的效果。同时,传统的蜂群算法在进行算法优化搜索过程中易陷入局部极值,在引入一致分布的佳点集理论进行算法初始化后,使种群分布均匀,可有效避免陷入局部极值。
2.2 佳点集
设GS是S维欧式空间中的单位立方体,即〈x〉∈Gs,〈x〉=(x1,x2,…,xs),其中0≤xi≤1,(i=1,2,…,s)。令γ∈GS,若点集
Pn(k)=({r1(k),r2(k),…,rs(k)}),k=1,2,…,n
(5)
有偏差
φ(n)=C(γ,ε)n(-1+ε)
(6)
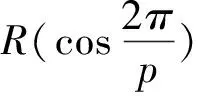
(7)
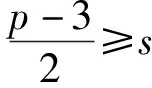
rk={ek},1≤k≤s
(8)
则称γ是佳点。其中,{an}表示an的小数部分。
2.3 一致分布
一致分布,又叫等分布,即数列{x(n)}在[0,1]上“等可能”分布,主要是为了研究小数的数字规律。其理论最早于1916年由H.Weyl在文献[15]提出,具体定义如下:
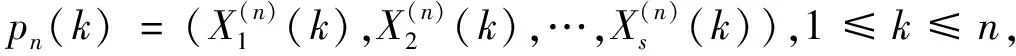
(9)
则称点集{Pn(k)}(0≤k≤n)存在φ(n)的偏差。
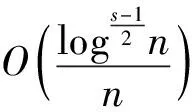
由华罗庚等在“数论在近似分析中的应用”对钟开莱、Kiefer定理的证明和文中的算法收敛性分析证明可知,一致分布的佳点集能够加快算法收敛速度。本文利用式(8)构造佳点集对人工蜂群算法进行种群初始化的改进,同时为了更好地提高算法的全局和局部搜索能力和种群的多样性和变异更新能力,本文将遗传算法中种群的交叉算子引入到全局最优解引导的人工蜂群算法(global artificial bee colony,GABC)中,提出一种基于一致分布佳点集改进的交叉人工蜂群算法(crossover of the global artificial bee colony,CGABC)。
2.4 交叉操作
在ABC算法中,算法的效率及收敛的关键是如何设计好适应度函数、种群的更新过程和如何避免陷入局部最优。在ABC算法中,引领蜂是在其领域中随机选取一个食物源进行迭代更新,这种方式更新得到的新食物源,在算法中不能保证它就是一个质量较好的解,可能导致算法局部搜索能力的下降。
交叉操作是将种群的父代个体基因中优秀的基因遗传给子代,通过配对方式进行基因交换重组,重新结合成新个体,在一定程度上充分提高了蜂群的多样性,提高了算法整体的优化能力。
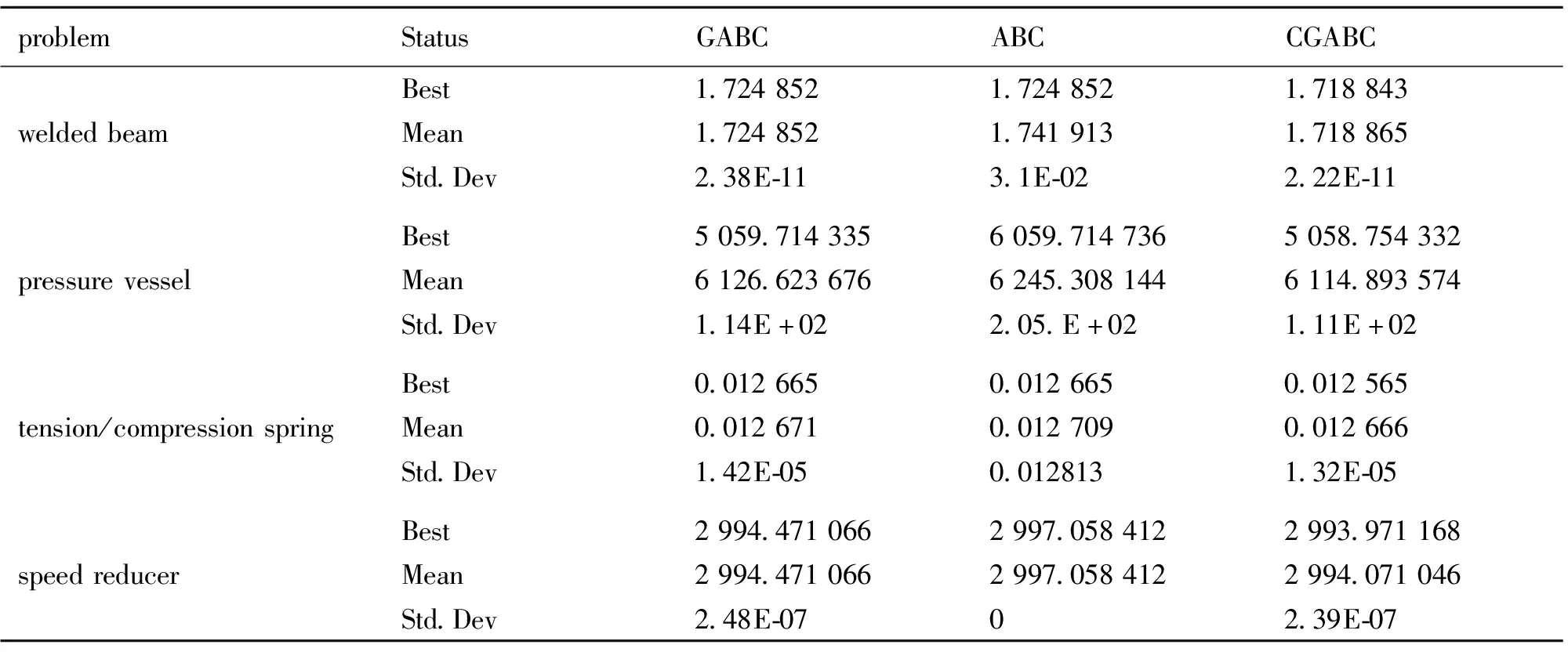
交叉操作常见方式有指数交叉和二项交叉两种[17]。交叉操作是将选择出的两个个体作为父个体,将二者的部分码值按位进行交换。在交叉操作中,对于二项交叉,对每一个分量都随机地产生一个0~1之间的随机数rand,若rand (10) 其中,交叉算子CR一般取值为0.3~0.6,β的取值在0~1.5。 为进一步提高算法的探索和开发能力,在G.P.Zhu和S.Kwong等提出的CABC算法思想启发下,通过全局引导来加快算法的收敛速度和算法搜索能力,具体领域搜索公式改变如下: (11) 其中,β的取值在0~1.5;α∈[-1,1]的随机值。 基于一致均匀佳点集的全局交叉人工蜂群算法(GCABC)借鉴了DE算法的基本思想和Zhu Guopu和Kwong Sam等提出的CABC算法思想,在CABC的基础上引入交叉算子,提高算法的种群多样性和变异更新能力,达到提高算法的开发能力和整体寻优能力效果。 CGABC算法步骤如下: S1:算法各种参数和基于佳点集的种群初始化。 S2:引领蜂(采蜜蜂)依据式(11)进行领域搜索,依据式(3)计算初始适应度值(fitness(xi))并记录全局最优值(GlobalValue)和全局最优解向量(GlobalMin)。 S3:进入采蜜阶段,引领蜂根据蜜源情况,采蜜蜂进行领域搜索,依据式(11)更新食物源,产生新的候选位置,并进行交叉操作。具体过程如下: While(iter 采蜜蜂将领域搜索后的解与迭代产生的最优解按式(10)进行交叉操作,计算新的适应度值,根据贪婪算法选择更优的蜜源; 计算观察蜂跟随概率(如式(4)所示),并转为采蜜蜂进行领域搜,然后按式(10)交叉操作,按照贪婪算法选择新的蜜源,并保留全局最优值; 侦察蜂随机寻找新蜜源替换超过领域搜索限制次数的蜜源; 记录全局最优解; End while 为进一步验证算法的合理与先进性,利用MATLAB 2013对下面的相关函数和工程设计问题进行了模拟仿真。具体仿真设计中采用参数设置如下:蜂群大小BN=50,采蜜蜂数量=观察蜂的数量=BN/2=25,所有优化函数维度D=30,最大迭代次数maxCycle=3 000,最大开采次数limit=1 500,交叉系数CR=0.4。实验针对每个测试函数在上述参数设置下独立运行10次,记录其最优值、平均值、最劣值和标准差。 为了充分测试CGABC的优越性,对文献[19]中的7个标准函数分别进行实验仿真,并与标准ABC算法和全局ABC算法的实验结果进行比较。7个标准测试函数如表1所示。 表1 测试函数 从表2中和图3~9的寻优收敛曲线图可以直观看出,不管是单模态还是多模态的函数,CGABC算法性能优于标准ABC算法和GABC蜂群算法,它能更快速地收敛于最优值点,效果有了明显提升。标准ABC蜂群算法和GABC蜂群算法所得出的结果与CGABC算法计算的结果比较,无论在精度还是在方差上都比CGABC算法差,且有时候会陷入早熟收敛问题。而改进后的蜂群算法有效地克服了标准蜂群算法的这些缺点。 表2 测试函数优化结果对比 图3 Sphere函数收敛 图4 Rosenbrock函数收敛 图5 Schaffer函数收敛 图6 Schwefel函数收敛 图7 Ackley函数收敛 图8 Rastrigin函数收敛 图9 Griewank函数收敛 为进一步验证算法的可用性和正确性,选用了文献[20]中的焊接梁设计(welded beam),压力容器设计(pressure vessel),拉伸/压缩弹簧设计(tension/compression spring)和减速器设计(speed reducer)4个工程问题(具体的工程细节描述和数学模型见参考文献[20])。 表3中详细列出了焊接梁设计、压力容器设计、拉伸/压缩弹簧设计和减速器设计4个工程问题的线性和非线性约束。表4可以明显看出3种不同算法之间的区别,无论是在最优值还是标准差方面本文的算法结果都比其他两种改进算法的结果更优。 表3 各种问题的线性和非线性不等式约束数 表4 CGABC与GABC算法、ABC算法优化4个标准工程问题的比较结果 人工蜂群算法是一种新型的群体智能优化算法,其具有特定的优化分工,采用贪婪选择和协作机制,算法灵活,不依赖于问题的梯度,具有广泛的适用性。本文对种群的初始化运用一致均匀的设计方法,并在优化过程中引入交叉算子对全局优化算法进行改进。实验结果表明,改进后的CGABC算法在优化单模和多模问题时均有较好的表现,均能提前全局收敛于函数的最优值,有效地平衡了算法的“局部开采”与“全局探测”能力,在一定程度上提高了算法的优化能力。3 CGABC算法框架
4 数值实验仿真与分析
4.1 函数优化仿真结果分析

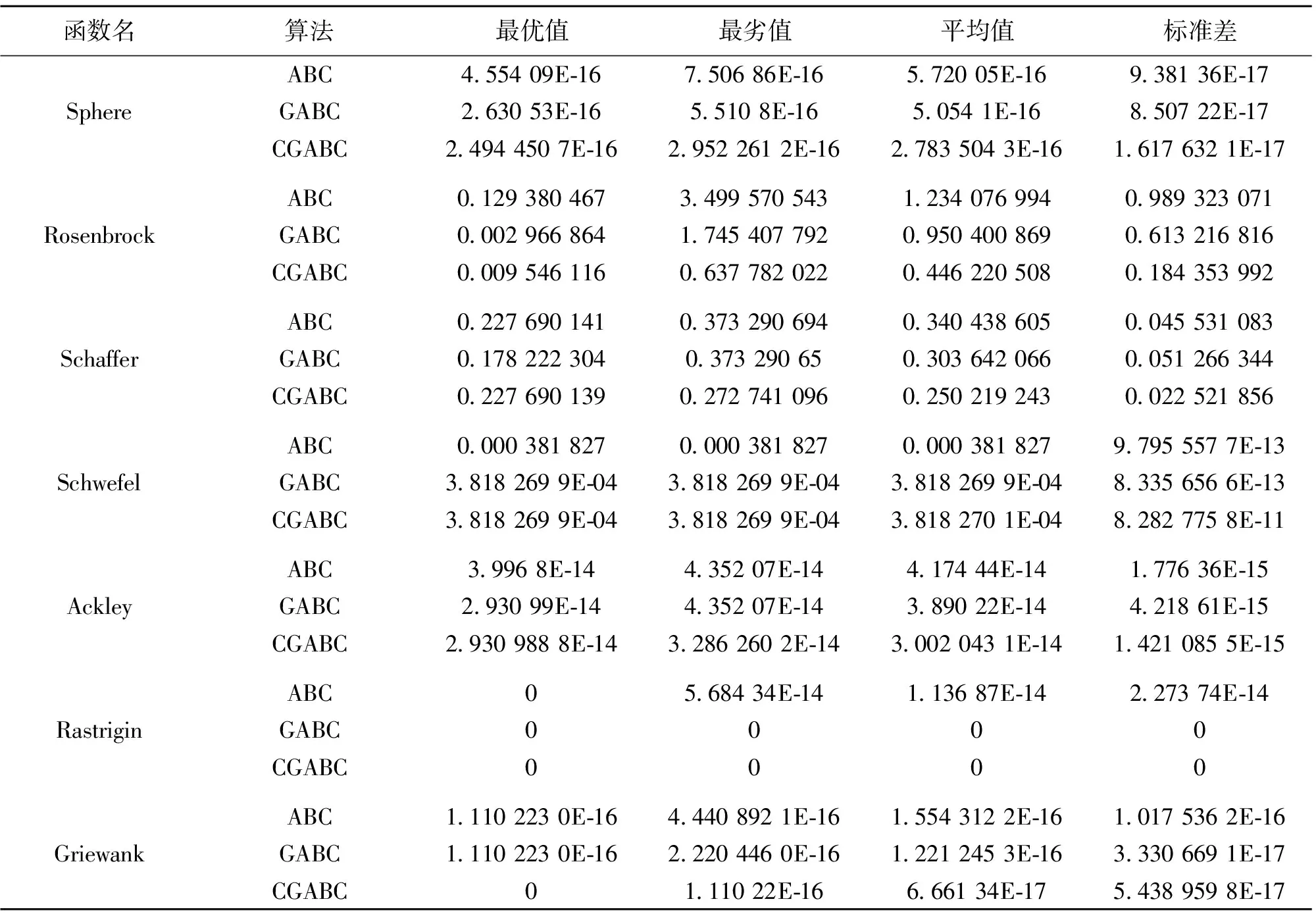
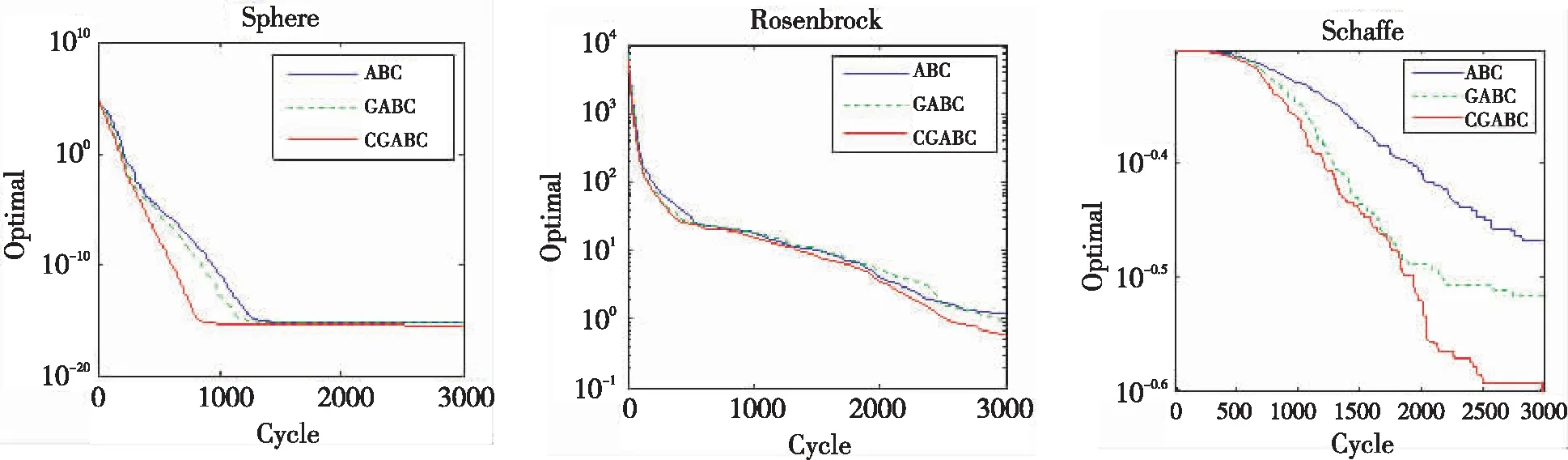
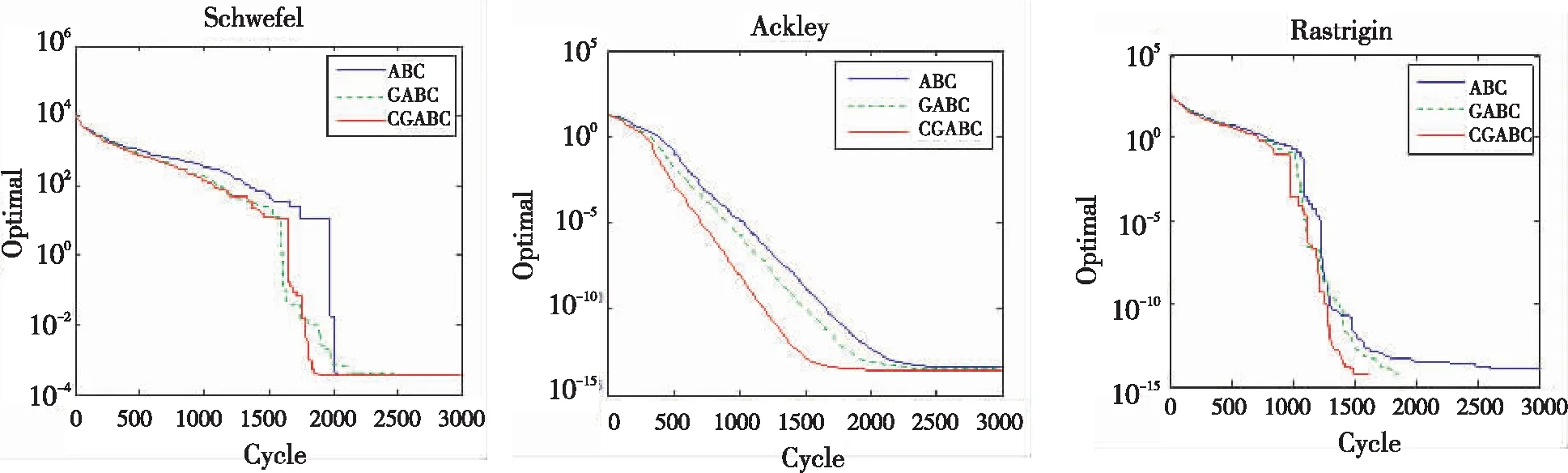
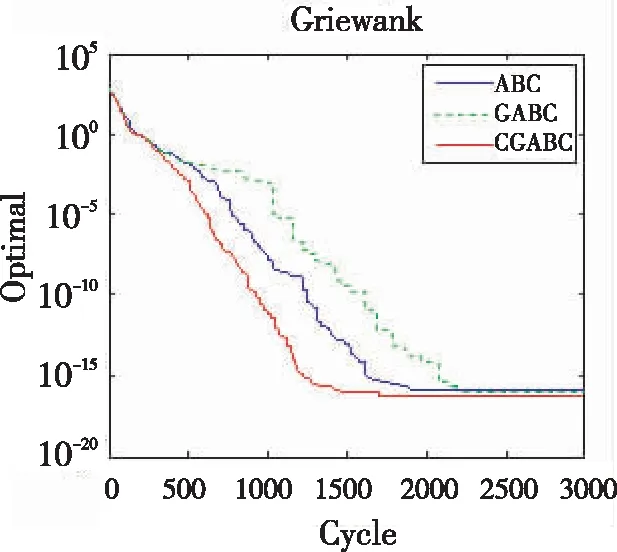
4.2 工程设计问题

5 结 论

