基于缺失点云的飞机表面锪孔质量检测

王红平，刘鑫，赵世辰，王宇，王磊

（长春理工大学 机电工程学院，长春 130022）

0 引言

随着工业领域新兴技术的发展，结构光相机的精度和实用性不断提升，已广泛应用于物体形状测量［1-3］、逆向工程等领域，其中基于点云的曲面拟合是逆向工程的一个重要研究分支。近年来，许多专家学者利用结构光相机对物体进行三维测量，并将三维点云数据拟合方法应用于物体检测［4］和参数估计［5］。锪孔在机械结构中起着重要的作用，特别在飞机装配行业中，如飞机骨架与蒙皮之间普遍采用铆接［6］，孔径尺寸、锪窝深度和法向偏差角度是否满足制孔质量要求是其连接精度和结构强度的重要保证。因此，刘华等［7］针对飞机蒙皮装配孔研制了一种集钻铣一体的多功能末端执行器，包括孔位补偿、法向量调整和锪窝深度控制等关键技术，但未针对检孔提出一套完整的方案；SCHNABEL R 等［8］研究了一种高效率的随机抽样一致算法（Random Sample Consensus，RANSAC）用于全局曲面拟合，包括对空间圆锥检测，具有很强的鲁棒性；王醒策等［9］改进了移动最小二乘算法实现局部曲面拟合，找到曲面准确法向，实现更复杂的细节，具有更高精度。上述研究中，其点云数据均是完整的，未考虑实际工况下因工件高反光、遮挡等因素造成点云缺失的情况。此外，毕运波等［10］利用双目视觉系统建立了沉头孔平行投影数学模型，将三维空间测量问题转换为二维平面测量问题，完成锪孔垂直度检测。同时撒继铭等［11］提出了一种利用圆曲线和圆锥曲面拟合方法，完成锪孔内外孔径和法向偏差角检测，该算法中锪孔法向偏差角测量利用圆锥表面任意三点其切平面必交于一点原理，以该点为圆锥顶点，建立圆锥数学模型，计算圆锥轴线的方向与外孔平面的法向量夹角。计算过程中利用圆锥表面任意三点法向量来计算其切平面，实际工程中点的法向量极易受到周围噪声影响，特别在锪孔部分缺失点云的情况下点的法向量检测更加困难。因此对锪孔法向偏差角检测精度具有不确定性。

综上所述，大多数现有的曲面拟合方法在拟合完整的点云数据时表现良好。然而在工业环境中，由于场景的复杂性，工件在扫描时出现遮挡、高反光，且受到噪声的影响，导致工件原始点云数据部分丢失，参数检测出现较大偏差；此外，复杂曲面上锪孔法向偏差角检测仍具有挑战性。针对上述问题，本文提出了一种基于正交投影法建立空间圆锥参数模型实现锪孔工件检测的方法，该方法采用了两种优化模型，解决了实际工况下点云数据缺失和曲面锪孔法向偏差角测量误差大等问题，提高了检测精度。具体方案是：1）对点云进行双边滤波处理，以减少离群点和噪声的影响；2）利用RANSAC 算法［12］分割上表面，根据边缘点云集中分布一侧特点提取上下边缘并拟合所在平面参数，再利用正交投影后锥角在平面XOY或平面XOZ满足傅立叶变换函数关系，计算出锪孔的锥角和锥点，建立精确的空间圆锥数学模型；3）通过锪孔上下边缘平面与空间圆锥数学模型进行数据融合，获取待检测的锪孔的参数，当空间圆锥轴线与Z轴出现偏差角时，其任意平面锥角变化曲线|F(x)max-F(x)min|与法向偏差角度满足Power 函数，从而大大提升锪孔法向偏差角度测量精度。

1 提取锪孔边缘信息

1.1 锪孔边缘数据点提取

由于散乱点云在数据存储结构中每个点是无规律排布的，在这样的数据结构中查找每个点的K近邻必须遍历所有点，因此必须建立点云数据的空间拓扑结构。本文采用KD 树法建立散乱点云之间数据结构，从而查询每个点Pi与其最近K邻域点集Ni=(i=0，1，…，k-1)。根据锪孔边缘点云分布情况，通过点的K邻域几何分布来判断该点是否为边缘点。若某一点为边缘点，则其K邻域点分布偏向某一侧如图1（a）所示；若某一点不是边缘点，则K邻域点均匀的分布在点Pi周围如图1（b）所示。

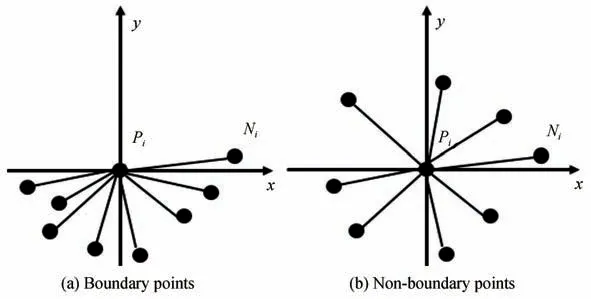
图1 锪孔边缘点分布Fig.1 Distribution of boundary points

以Pi和K邻域点集Ni为样本点，利用最小二乘法拟合局部平面Si，Si满足

平面Si法向量n(A，B，C)，K邻域样本点Ni投影到Si平面

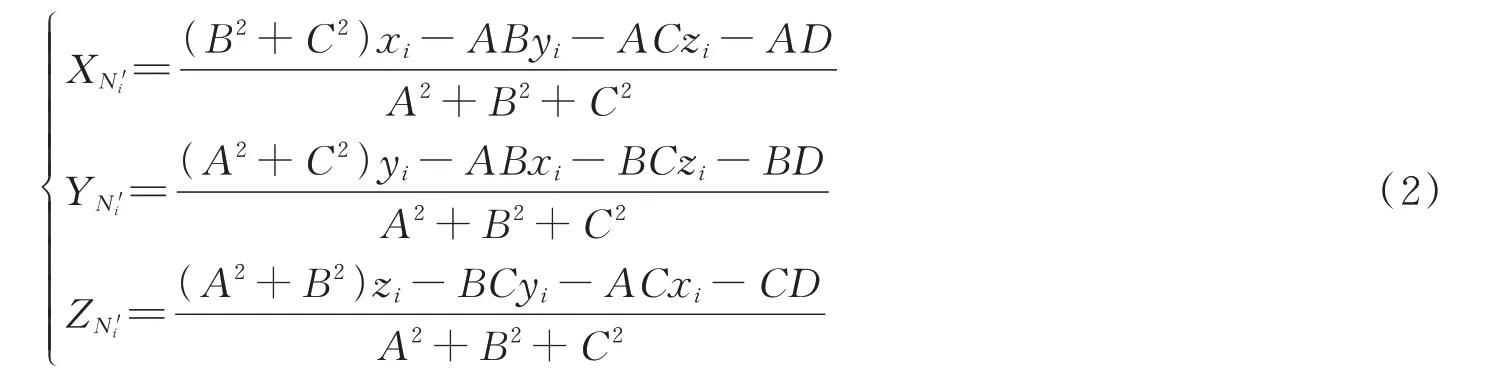
从式（2）可知点集Ni投影平面Si后，其投影后点集N'i(i=0，1，…，k-1)。构建局部二维平面坐标系，取平面内任意一点，使得，在局部平面Si坐标系满足

在Si平面内为X轴，从式（3）得到Y轴，Pi为坐标原点。则平面Si内相邻向量之间夹角θi满足

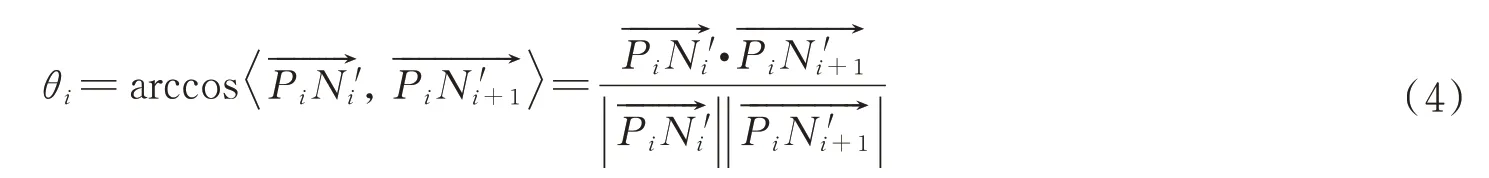
由式（4），计算Si平面内相邻向量之间夹角最大值θmax

θmax与设定阈值120°比较，当θmax＜120°时，提取上下边缘点。

1.2 下边缘预处理及其边缘平面拟合

实际工程中由于工件材料问题，不同材料工件，激光在锪孔下边缘发生不同程度的反射和衍射现象，导致激光过于集中，或者发生偏转。因此对其下边缘点云数据预处理。对已提取下边缘点计算Z轴方向点的平均值Zmean和Zstd，即

当Zi-Zmean＜Zstd时，保存其下边缘点集。

锪孔上下边缘平面拟合步骤：1）利用双边滤波［13］对原始点云进行降噪处理；2）根据工件高度确定边缘点Pi范围，查询该范围内所有邻域点集Ni；3）对样本点Ni数据利用最小二乘法拟合平面，并且建立局部空间坐标系；4）在局部平面内计算各点向量之间夹角，分割出来上下边缘点，并且对分割后下边缘点云数据进行预处理；5）利用RANSAC 拟合上下边缘所在的平面得到其精确的平面参数。

2 锪孔曲面拟合算法

2.1 空间圆锥数学模型建立

锪窝曲面可视为圆锥曲面一部分，本文提出建立空间圆锥数学模型，代替待检测的锪孔曲面，完成锪孔参数检测。空间圆锥数学模型如图2 所示。

图2 空间圆锥示意图Fig.2 Schematic diagram of space cone

图2 所示空间圆锥的参数包括圆锥的锥角θ、圆锥轴线Le、顶点P0。根据锥面的几何特征，当圆锥锥点P0(x0，y0，z0)、锥角θ、轴线Le方向确定时，可以确定空间唯一圆锥方程。图3 为经过RANSAC 分割锪孔上表面和锪孔下边缘处理之后的得到新的点云集

图3 锪孔点云预处理过程Fig.3 Countersinking point cloud preprocessing process

在实验过程中，以多激光传感器为标定方案［14］，使相机垂直工件表面进行拍摄。以结构光测量系统中坐标系为基准，建立点云空间直角坐标系，以便将预处理后点云正交投影到平面XOZ和平面YOZ。投影到平面点满足

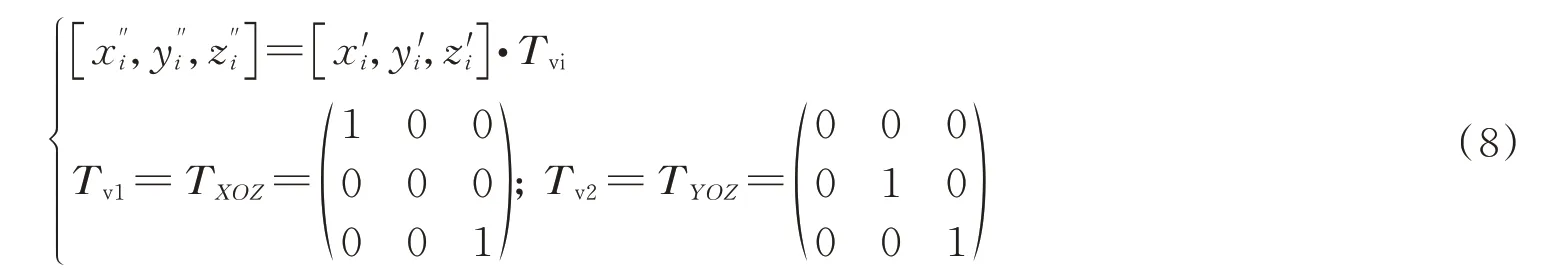
由式（8），投影到平面XOZ的点集，投影到平面YOZ的点集

如 图4 所 示，根 据RANSAC 算法拟合平面XOZ和平面YOZ内直线L1、L2、L3、L4，其方向向量分别为a1，b1，a2，b2，设圆锥锥角θi=(θi1，θi2)，则锥角θi满足

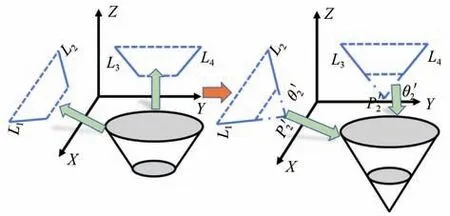
图4 正交投影构建空间圆锥示意图Fig.4 Schematic diagram of constructing a space cone by orthogonal projection

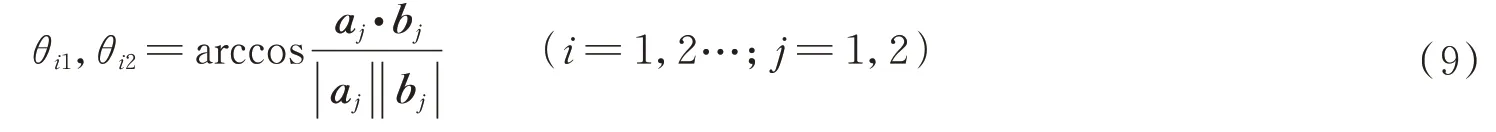
由式（9），可得到空间圆锥锥角参数θi。

表1 所示为锪孔点云通过正交投影法投影到XOZ平面的锥角边缘点数与异常点数对比。其异常点主要来源于工件高反光造成的点云数据缺失，在提取边缘点时误将内部点提取出来。由图5 比较RANSAC 和移动最小二乘算法拟合锥角参数可知，移动最小二乘拟合算法在完整的点云数据上表现良好，但针对异常点云值时这种方法会造成很大误差和较低的鲁棒性，RANSAC 算法则表现稳健，从包括“异常值”的一组观测数据中迭代估计已知数学模型参数，消除异常点干扰，因此本文采用RANSAC 算法。

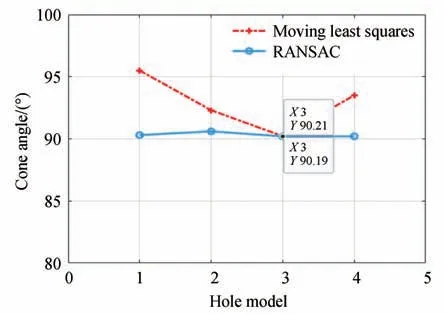
图5 圆锥锥角拟合方法对比Fig.5 Comparison of cone angle fitting methods

表1 锥角边缘点数分布Table 1 Point distribution of cone angle boundary

本文提出的建立圆锥模型进行锪孔参数检测的方法，对投影后检测锥角的精度要求较高。因此提出一种数学模型（傅立叶级数）对已获得圆锥锥角进行参数优化。由于空间圆锥在平面XOZ和平面YOZ上投影，其锥角投影周期为π 符合傅立叶级数特性，因此在平面XOZ或平面YOZ投影后圆锥锥角满足数学模型

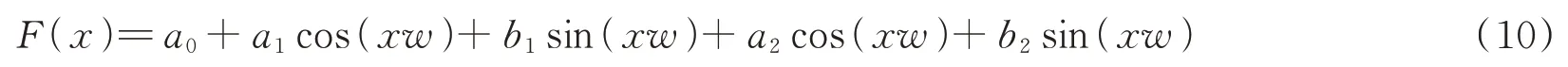
图6 为傅立叶级数曲线仿真结果，图中表示空间圆锥参数为锥角90°，法向偏差角3°，拟合后的误差平方和

图6 锪孔锥角拟合示意图Fig.6 Schematic diagram of plane cone angle fitting

2.2 锪孔法向偏差角度检测

针对曲面锪孔上表面参数方程较为复杂并且计算困难等问题，本文对此提出Power 数学模型，检测锪孔的法向偏差角度。当圆锥轴线与Z轴产生不同的偏差角时，基于2.1 节锥角在平面XOZ或平面YOZ面投影后的变化曲线，建立某一投影平面内θdif（θdif=|max(f(x))-min(f(x))|）与法向偏差角的关系，可得到平面XOZ或平面YOZ投影后圆锥角度的极值差θdif与法向偏差角度θstd关系（如图7），可表示为

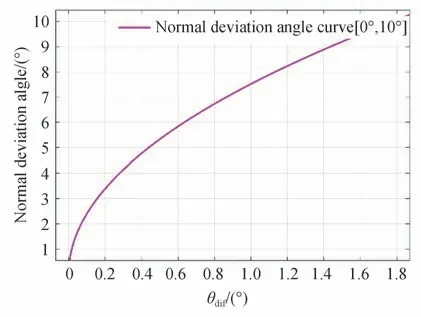
图7 锥角极值差与法向偏差角曲线Fig.7 Normal deviation angle curve

拟合后的相关系数R2为1，（R2可衡量回归方程整体拟合度），残差范数为5.1×10-4。

2.3 锪孔几何参数检测

由式（12）可计算出轴线Le方向向量s，所以Le方程为，同理：圆锥旋转曲面母线F(x，y，z)=0，在母线F(x，y，z)任取一点M1=(x1，y1，z1)，则过M1的纬圆上任意一点P(x，y，z)，满足

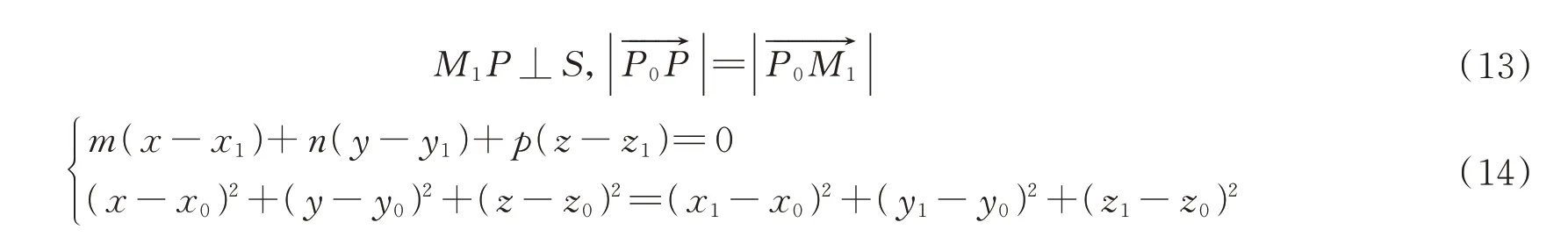
结合圆锥母线方程F(x1，y1，z1)=0，可得空间圆锥旋转曲面。

本文锪孔曲面拟合算法步骤为

1）对原始点云进行预处理，提取锪孔上下边缘，拟合上下平面参数。

2）利用正交投影法得到空间圆锥模型参数：锥点P0，锥角θ，锪孔法向量偏差角度，并确定空间唯一圆锥方程。

3）通过锪孔上下边缘平面与空间圆锥方程数据融合，最终完成锪孔参数检测。

3 实验与结论

3.1 实验平台搭建及算法流程

检测系统主要由机器人系统、视觉检测系统和上位机等组成，其中机器人系统、视觉检测系统与上位机之间通过TCP/IP 协议进行通讯。实验平台搭建如图8 所示，由fanuc-m20ia 六轴机器人、计算机、结构光相机和四激光传感器等组成，视觉检测装置通过法兰挂载到机器人末端。使用2.9Hz CPU 和8GRAM 内存笔记本电脑，通过matlab R2018b 对点云进行处理。实验分为四组（如图9）：a）标准锪孔；b）异面锪孔；c）高反光锪孔；d）曲面锪孔。图10 为不同工况下分割上平面后的锪孔的点云图。

图8 实验系统Fig.8 Experimental system diagram

图9 不同工况下的锪孔Fig.9 Counterbore under different situations

图10 不同工况下分割上平面后的锪孔的点云图Fig.10 Point cloud after segmentation

本文所提方法对下边缘点进行预处理是至关重要的，下边缘处理直接影响锪孔内孔直径参数检测。将获取的下边缘点云数据集，经过Zi-Zmean＜Zstd预处理后导入Matlab 软件中，其中X，Y坐标表示下边缘位置信息，颜色表示预处理后的点集在下边缘平面法线方向偏移量。如图11 所示。

如图11所示，根据下边缘平面度可知，其负法向偏差最大为-0.002 1 mm，正法向偏差最大为0.061 3 mm，平均值为0.026 4 mm，法向方差为0.000 5 mm。下边缘平面度证明了下边缘点预处理能够使其绝大部分点在同一空间平面上，保证了锪孔内孔径参数检测精度。

图11 下边缘平面度Fig.11 Flatness of lower edge

3.2 锪孔质量检测参数研究

建立锪孔锥角参数优化模型，根据正交投影法对3.1 节提到四种锪孔进行检测，以Z轴为旋转轴，周期为[0，π]，步长为π18，在平面XOZ上进行投影。锥角在平面XOZ投影后拟合曲线如图12 所示，其锥角F(θa)=89.901°，θdif=0.444°、F(θb)=89.949°，θdif=0°、F(θc)=89.903°，θdif=0.164°、F(θd)=89.951°，θdif=0.072°。由于锪孔法向偏差角度θstd与θdif（θdif=|max(f(x))-min(f(x))|）满足θ(x)std=7.518(θdif)0.496，因此锪孔法向偏移量分别为5.025°，0°，3.066°，2.038°。

图12 锥角参数曲线Fig.12 Cone angle parameter curve

通过与机器视觉、移动最小二乘曲面拟合算法的比较对本文方法进行了验证。表2 是不同方法的锪孔内孔径、锥角、法相偏差角和锪孔深度参数提取结果。

已知本文检测的四种锪孔，其内孔直径的真实值分别为10.011 mm、5.996 mm、5.990 mm 和6.010 mm，从表2 可得，机器视觉内孔直径拟合的最大误差为0.123 mm，移动最小二乘算法拟合的内孔直径最大误差为0.246 mm，上述两种方法内孔的最大误差均来自孔3 工件高反光的影响。本文方法获得的内孔直径最大误差为0.023 mm，相比于机器视觉和移动最小二乘算法在精度上分别提高了81.3%和90.65%，并且本文方法检测得到的锪窝深度最大误差与上述两种方法相比，也具有较高的鲁棒性。此外，上述四种锪孔锥角真值分别为89.973°、89.806°、90.022°、89.879°，从表2 可得，机器视觉锪孔锥角检测的最大误差为0.521°，移动最小二乘算法锪孔锥角检测的最大误差为0.604°。本文方法检测得出最大误差为0.121°，相比于移动最小二乘算法和机器视觉方法分别降低了79.96%、76.77%。锪孔法向偏差角真实值为0.003°、2.926°、4.904°、2.150°。在缺失点云情况下，本文方法得出的四种锪孔法向偏差角最大拟合误差不超过0.142°，相比机器视觉和移动最小二乘算法误差降低了71.9%和70.6%。因此，上述实验验证了本文所提方法具有更高的检测精度。

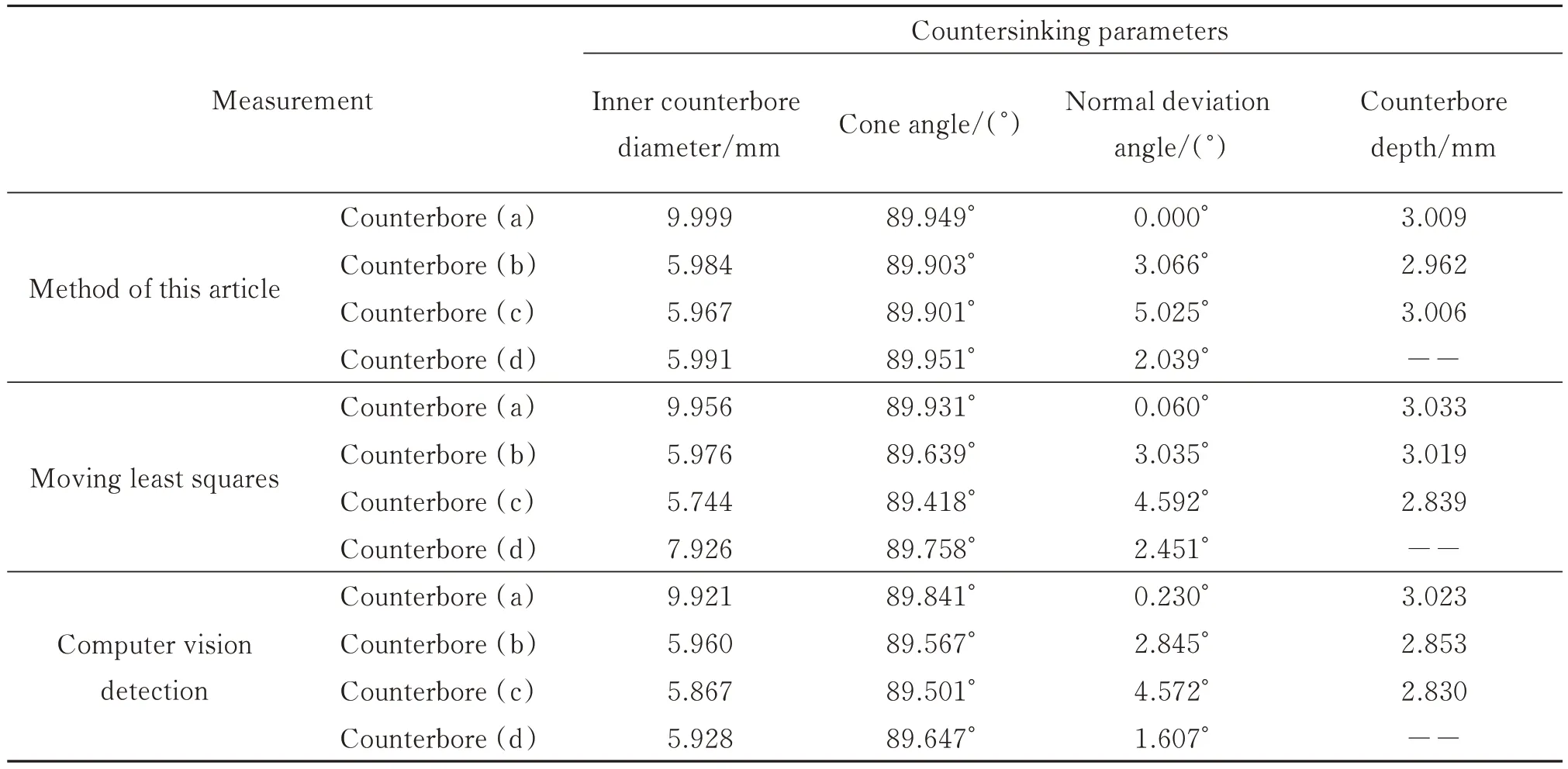
表2 本文方法与其他方法对比Table 2 The comparison between the method in this paper and other methods

本文对易发生高反光铝合金材料上的锪孔进行检测。图13（a）为结构光相机检测工件流程，13（b）为三坐标测量仪检测过程，图13（c）平面锪孔加工样件，板材工件尺寸为200 mm×200 mm×50 mm，由铝合金5 052 制成。图13（d）为曲面锪孔加工样件，板件尺寸为200 mm×140 mm×h（10＜h＜5）mm，由铝合金6 061制成。本实验分为两步：第一步，利用三坐标测量仪、窝量规和千分尺对平面和曲面上的锪孔的法向偏差角度、深度和孔径进行测量；第二步利用结构光相机对工件测量。

图13 本文方法、三坐标测量仪检测流程和测量工件Fig.13 3D vision and 3D inspection process and the workpiece

表3 为平面锪孔样件真实值与本文方法检测结果对比。在四种不同类型的平面锪孔中内孔直径误差最大为-0.023 mm，深度最大误差为-0.022 mm，法向偏差角度最大误差为-0.13°。由此得出，本文方法即使在易发生高反光工件上，依然有较高的检测精度。

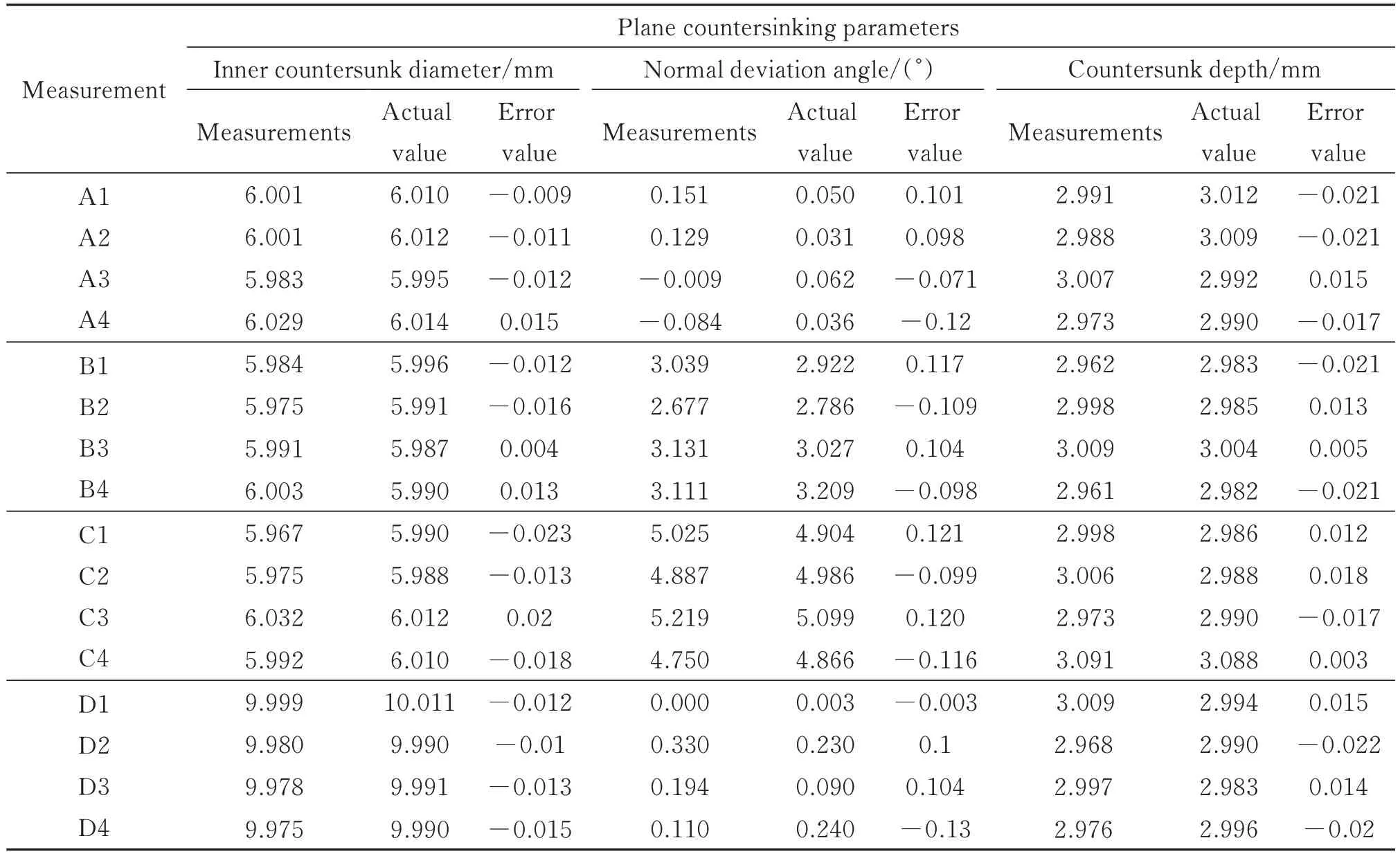
表3 平面锪孔检测Table 3 Plain counterbore inspection

图14 为表4 中曲面法向偏差角度测量结果分析图，其最大误差为0.136°，进一步验证了本文所提方法的准确性和稳定性。值得一提的是，从本文方法原理出发，锪孔的法向偏差角θstd是由锪孔锥角在空间坐标平面XOZ/YOZ投影的极值差θdif通过Power 函数计算得出，因此本文提出的拟合方法针对不同曲率工件上的锪孔依然有较高的检测精度。

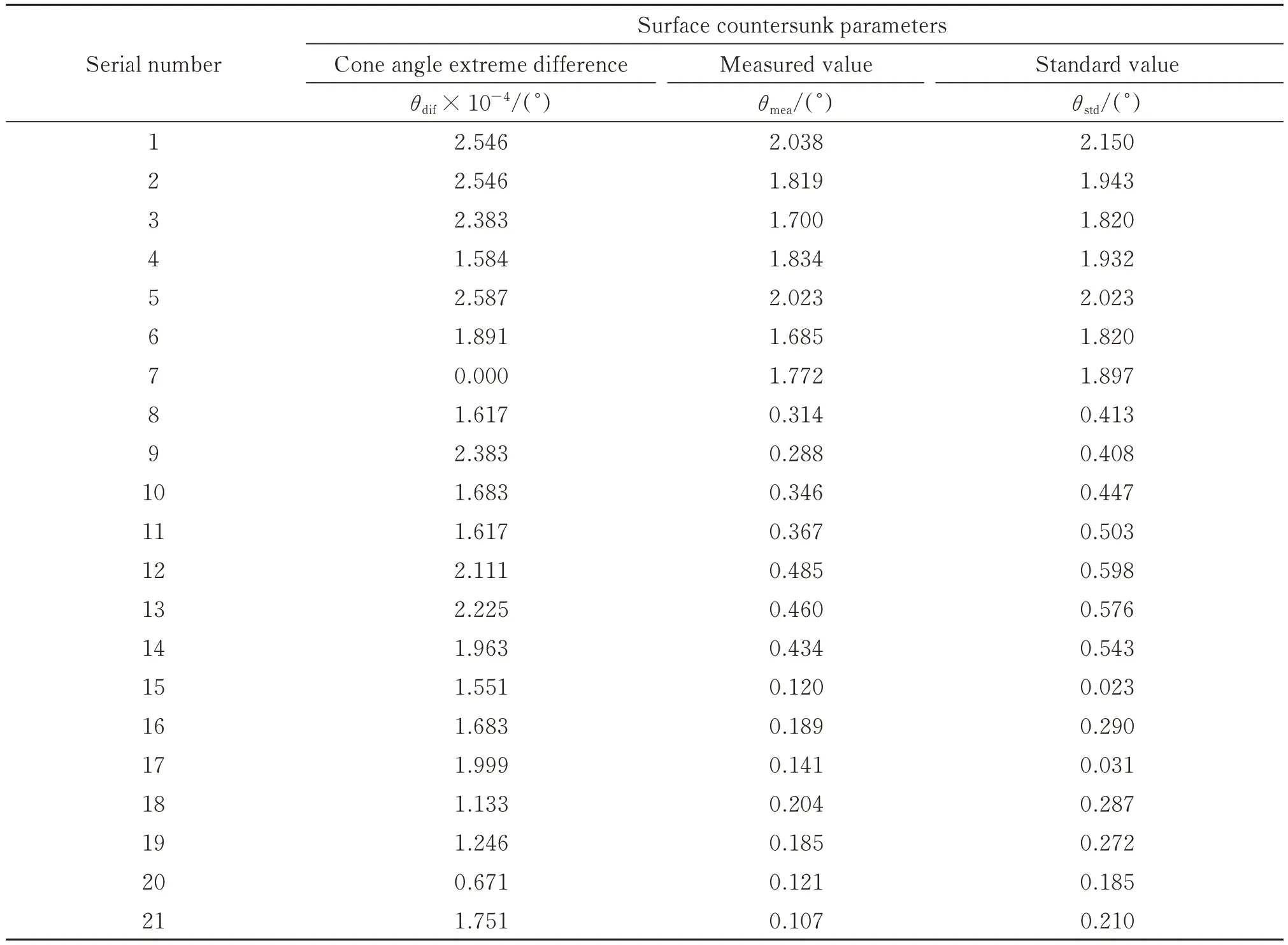
表4 曲面锪孔法向偏差角测量Table 4 Measurement of normal deviation angle of counterbore on complex curved surface

图14 曲面法向偏差角度分析Fig.14 Analysis of normal deviation angle of curved surface

4 结论

为了提高锪孔检测过程的精度和鲁棒性，本文提出了一种结构光锪孔检测方法。针对实际复杂工况下结构光相机获取的工件点云数据部分缺失的问题，以易发生反光的铝制工件为样本进行了大量的图像采样及处理。本文方法获得的不同类型锪孔法向偏差角误差小于0.142°、平面工件孔径误差小于0.025 mm、孔深误差小于0.022 mm。实验结果表明本文方法检测的锪孔的上述四个指标参数优于传统机器视觉和移动最小二乘曲面拟合算法，一方面能很好地消除部分点云缺失情况下的信息干扰，另一方面能有效地提高复杂曲面上锪孔法向偏差检测的结果，检测精度高、抗噪性能好。