光场成像回波解调比法抑制光强扰动像质退化

程志远，纪洲，高彦生，苏华，闫佩佩，夏爱利

（1 中国科学院西安光学精密机械研究所，西安 710119）

（2 中国科学院空间精密测量重点实验室，西安 710119）

（3 中国科学院大学，北京 100049）

（4 陕西师范大学 物理学与信息技术学院，西安 710119）

0 引言

激光光场成像技术可通过主动发射多束激光扫描目标，并采用多探测器阵列接收解调激光回波能量信号，重建目标高分辨图像［1-2］。该技术在空间目标观测、遥感成像等领域具有广阔应用前景。多光束干涉光场成像技术本质上是一种新型计算光学技术［3］，基于光信息处理理论提高目标信息获取量［4］。激光光场成像技术在接收端不需要高面型精度的光学镜面，有望突破传统光学成像技术对相机口径、镜面面型等约束，共焦不共面、低面型要求的光学接收器和点探测器阵列具有低成本的特点，可以在提高分辨率的同时节约光学制造成本。

美国先后启动了GLINT（GEO Light Imaging National Teseted）项 目［1］和SAINT（Satellite Active Imaging National Testbed）项目［2］，分别用于对高轨和低轨空间目标成像。俄罗斯学者随后在激光发射阵列和激光散斑等方面开展了研究［5］。国内学者针对激光光场成像技术的研究侧重点各不相同，均取得一定研究成果。中科院光电院针对光场成像分辨率［6］、大气湍流畸变等开展研究［7］；中科院长春光机所开展非均匀采样技术等研究［8］；电子科技大学开展了天线阵列方面研究［9］；国防科技大学开展了信号全相位谱方面的研究［10］；中科院西安光机所针对成像像质评价［11］和散斑噪声抑制［12］等开展研究。多光束光场成像系统在频谱采样过程中要求光束光强保持恒定，而在实际工程应用中，光束光强扰动引起的频谱重建误差影响成像质量。已有研究表明，光束光强扰动是影响成像质量的一个主要因素［13-16］。

为此国内外学者关于光束光强扰动抑制开展了研究：CUELLAR E L 等主要研究了光场成像系统在大气湍流效应影响下的图像重建研究，并未针对光束光强扰动专门进行研究［17］；RHODES W T 等采用长时间采样取平均方法抑制光强闪烁等，该方法采样时间变长，成像的实时性受到限制［18］；李丽艳等开展了基于相位载波解调抑制光强扰动研究［19］，主要解决激光后向散射光强扰动问题等。以上学者分别针对光束光强扰动不同侧重点，都取得了一定的研究进展。有别于现有光强扰动抑制研究视角和研究方法，本文提出一种基于计算光场回波信号解调比的方法，抑制重建频谱信号中光强扰动因子随机变化带来的频谱误差，以提高重构图像质量，并通过仿真和桌面实验平台进行验证。

1 光强扰动对光场成像频谱分量的影响模型

1.1 光场成像原理

激光光场成像系统如图1 所示，主要由发射器和接收器两部分组成，发射端的频率调制器调制激光阵列发射的多束激光，光束形成干涉条纹光场扫描目标，携带目标频谱信息的光场回波信号经目标反射，被大面积接收器汇聚接收，再由多光束相位闭合技术消除大气湍流相位畸变后，重建各阶频谱分量，最后由信号处理算法重建目标图像。激光光场成像技术通过扩展激光束孔径之间的干涉基线长度提高分辨率，具有口径容易做大、分辨率高的特点。

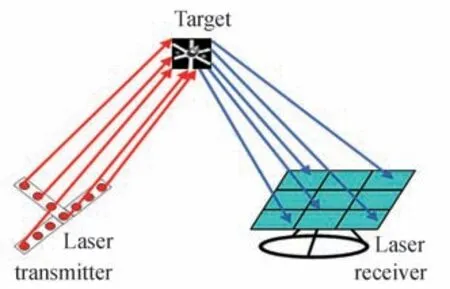
图1 光场成像原理示意图Fig.1 Schematic diagram of optical field imaging principle

1.2 光场回波信号解调

在光场成像方面，目前国内外主要以三光束光场成像系统研究为主，三光束激光光场成像系统是光场成像的最小配置，也是最基本的单元，可以完成相位闭合和重构成像，若光束数低于3，则无法完成相位闭合和频谱重建。对于三光束光场成像系统和多于三光束的多光束光场成像系统，解调比分析方法基本原理都相同。因此基于三光束激光阵列光场成像系统，研究激光束光强扰动和湍流扰动对光场成像像质影响理论模型，该模型可直接推广应用于多于三光束的光场成像系统中。

三光束光场成像发射阵列发射3 束激光对距离R处的目标照射，3 束激光干涉场扫描目标反射的光场回波信号S（t）可表示为

式中，I（x，y，t）为光强函数；O（x，y）为目标强度反射率函数；三束光光强振幅分别为A1、A2、A3；Δωij为光束i和光束j的频率调制差；Δφij为光束i和光束j由于大气湍流引起的光学相位差；λ为激光光波波长；R为成像距离；fxij，fyij分别为发射阵列坐标位置，ij=12、13、23。

光场回波信号处理过程中，需要将光场回波信号表达式（1）中的3 个不同频率信号解调出来，假设光学接收阵列探测器收集到的光场回波离散数据为M（kT），k为离散采样点序号，当信号采样点数N、信号采样周期T、信号频率调制差Δω满足条件NΔωT=2nπ，对激光回波信号解调，分别计算得到光束1、光束2、光束3 三光束中两两光束之间的信号解调分量P12、P13、P23为

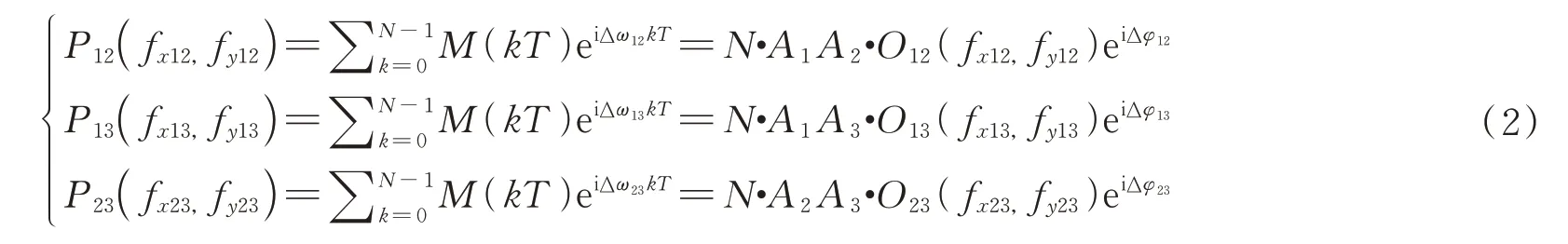
由式（2）可知，激光回波信号解调分量P12、P13、P23分别受三束光光强振幅A1、A2、A3中对应两束光光强振幅影响。

1.3 光强扰动对光场成像频谱的影响模型

首先对光场回波信号解调处理，再进行相位闭合处理计算相位闭合系数，然后依据等频谱迭代重建原理，依次求解各阶频谱分量O12、O13、O14、…，与现有频谱模型不同，基于光强扰动因子思路推导建立得到了与光强扰动因子A2(ti)2相关的频谱模型O1n为

式中，R12n为相位闭合系数；A2(ti)2定义为光强扰动因子，A2（ti）为光束2 在ti时刻的瞬时光强振幅，该值随时间变化，是高阶随机变量，由于该值随机变化，在频谱重建过程中，频谱重建误差被迭代放大，直接影响重构图像质量。在实际应用中，由于光束光强存在波动效应，光束2 光强振幅随机波动，影响频谱重建精度，进而降低成像质量。

2 光场回波解调比法抑制光强扰动

通过理论推导与分析可知，为消除光束光强扰动对像质影响，应抑制光强扰动因子A2(ti)2对频谱重建分量的影响。针对大气湍流对光束相位影响较小的弱湍流实验场景，采用激光回波解调比法消除光束光强扰动引起的光场像质退化效应。

基于解调比法抑制光强扰动光场成像步骤如图2 所示：首先进行光场频谱采样，然后进行光场回波信号解调，计算光场回波解调比，再由回波解调比求解光强扰动因子，相位闭合处理后消除光强扰动因子对频谱分量的影响，最后逆傅里叶重建图像。

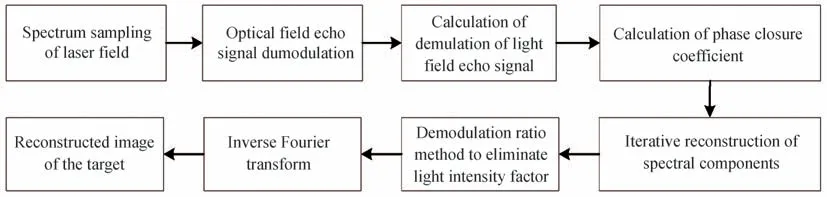
图2 解调比法抑制光强扰动示意图Fig.2 Schematic diagram of suppression light intensity disturbance by demodulated ratio method

在湍流较小或室内实验等场景，湍流引起的随机相位差Δφij由相位闭合技术抑制后可近似为0，大气湍流引起的相位扰动可忽略，光场回波解调表达式（2）可近似表示为

基于等频谱采样模式，由式（4）中3 个解调信号分量，可分别得到tn时刻，光束1 与2、光束1 与3 的光强振幅平方的比例系数为

2.1 求解相位闭合系数

光场回波信号S（t）解调处理后得到光场解调信号Pij，再由激光回波解调分量Pij迭代重建相位闭合系数R12n，即

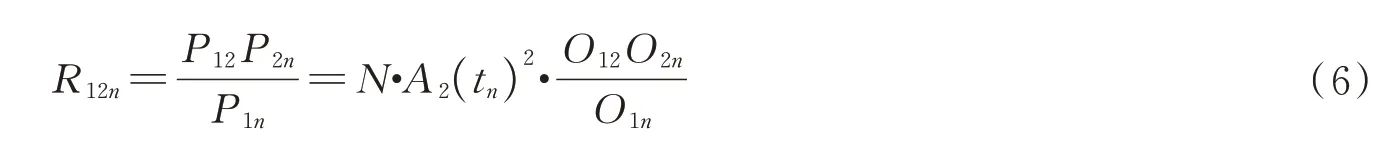
式中，n为频谱采样点序数，取值为3、4、…、n-1、n；A2（tn）受光束光强扰动和大气湍流扰动影响，光束光强无法保持恒定，故相位闭合系数R12n为随光束光强和时间变化的随机变量。

2.2 求解各个时刻光强随机扰动因子

采用频谱重建方法解算得到频谱分量O1n

式中阶频谱分量O1n受光强扰动因子影响，故存在求解误差，进而影响重建图像像质。

采用解调比法消除光强扰动因子A2（tn）2对频谱信号O1n和成像质量的影响。由光强比例系数Bn_12的表达式（5）可得

就t1时刻这一瞬时特定时刻而言，光束1 光强振幅平方值A1（t1）2可用常数C=A1（t1）2表示，tn时刻光束2 光强扰动因子A2(tn)2可表示为

在光场成像频谱重建算法中，由频谱采样时刻t1低阶频谱O12逐步迭代重建高阶频谱分量O13、O14、…、O1n，后续的高阶频谱O1n只与t1特定时刻的光强瞬时取值有关，因此可以把特定t1时刻光束1 的光强振幅视为常数C。

2.3 抑制激光光强波动的频谱求解与像质评价

将激光束光强扰动因子的计算公式（9）代入式（7），再采用频谱重建技术如图3所示，计算得到频谱分量O13为

图3 频谱迭代重建示意图Fig.3 Schematic diagram of spectrum iterative reconstruction

从低阶频谱O13迭代计算得到次高阶频谱O14为

再依次迭代递推得到高阶频谱O1n为

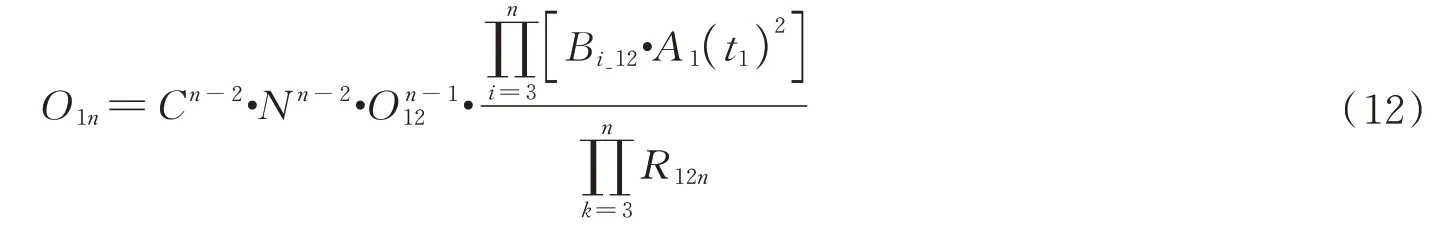
由各阶信号频谱分量O1n逆傅里叶变换得到目标图像，并计算目标图像的像质指标评估重建图像像质。

2.4 像质评估方法

本研究用峰值信噪比、斯特列尔比、结构相似度进行重建图像像质评价。

1）峰值信噪比

峰值信噪比（Peak Signal-to-Noise Ratio，PSNR），是原图像与被处理图像之间的均方误差相对于（2n-1）2的对数值。峰值信噪比越大，两幅图像越接近。计算公式为

式中，MSE 为两幅图像的均方误差。

2）斯特列尔比

斯特列尔比（Strehl Ratio，SR）表示重建前后图像强度分布的互相关谱，由重构图像与原始图像的强度分布归一化处理计算得到，表征重建图像与原始目标图像的光强分布相似程度。斯特列尔比取值范围介于0 和1 之间，最大值为1，两幅图像越接近，斯特列尔比值越大，也越接近1，其定义为［14］

3）结构相似度

结构相似度（Structural Similarity，SSIM）是一种用来衡量两幅图像相似度的指标，定义为亮度、对比度和结构三个不同因素的组合。用均值作为亮度的估计，标准差作为对比度的估计，协方差作为结构相似程度的度量。结构相似度值越大，两幅图像越相似。结构相似度函数为

一般设α=β=γ=1，最后把三个函数组合起来，得到SSIM 函数为

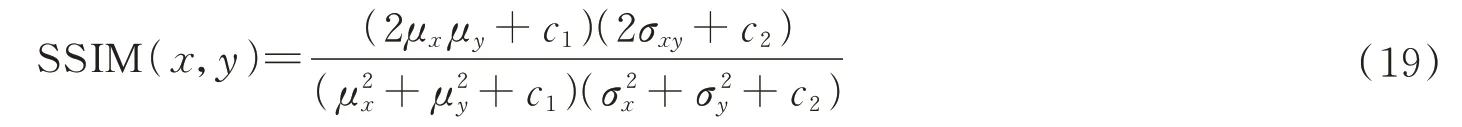
式中，μx是图像x的灰度平均值，μy是图像y的灰度平均值；σx是 图像x的灰度方差，σy是图像y的灰度方差，σxy是图像x和图像y的协方差；c1=(k1L)2，c2=(k2L)2，c3=c2/2，是用来维持稳定的常数；L是像素灰度值的动态范围，k1=0.01，k2=0.03。

3 实验和结果分析

为了验证解调比法抑制激光束光强扰动的实际效果，分别采用仿真和桌面实验验证平台进行比对分析。

3.1 仿真与结果分析

模拟激光光束不同强度光强扰动下的光场重建图像像质，并计算不同光强扰动下的重构图像斯特列尔比值。光束光强扰动（Beam Intensity Disturbance Ratio，BR）定义为激光光束光强扰动方差值与光束光强均值的比值，该值用于表征光强扰动强度的大小。表1 为激光光束不同强度光强扰动下直接重建图像的斯特列尔比，仿真激光束光强扰动（BR）变化范围为0%～15%，受光束光强扰动影响，直接重构图像斯特列尔比从0.85 下降到0.31。表2 与表1 为同样光强扰动下，解调比法重建图像的斯特列尔比值。对比可知，在同样强度光束光强扰动下，表2 的斯特列尔比值明显高于表1 的图像斯特列尔比值。

表1 不同强度光强扰动下直接重建图像斯特列尔比值Table 1 SR of direct reconstructed image under different BR

表2 不同强度光强扰动下解调比法重建图像斯特列尔比值Table 2 SR of demodulated ratio reconstructed image under different BR

图4（a）和（b）分别为卫星目标仿真输入图和激光光束无光强扰动时直接重建得到的卫星目标图像，无光强扰动时BR=0%，重构图像斯特列尔比SR=0.85。

图4 原始仿真目标和无光强扰动下重构图像Fig.4 Original simulation target and reconstructed image without light intensity disturbance

在光场成像系统中，由于图像初始相位无法求解得到，初始相位未知，相位延拓导致出现4 个图像如图5所示。图5（a）～（f）分别为激光光束在光强扰动变化范围1%～15%时直接重构得到的目标图像。图5（g）～（l）为在同样光强扰动范围下，采用解调比法抑制光束光强扰动后，重构得到的目标图像。对比可知，解调比法重建得到的图像像质更好，重建图像轮廓清晰，图像背景均匀，图像斯特列尔比值更高。当光强扰动达到10%时，直接重建图像图5（d）已无法分辨目标形状，采用解调比法重建图像图5（j）中的卫星目标轮廓更清晰，斯特列尔比也更高。当光束光强扰动强度达到13%时，图5（e）、（f）图像目标模糊一团，目标形状已无法重建。

图5 直接重建和解调比法抑制光强抖动前后重构图像对比Fig.5 Comparison of reconstructed images by direct reconstruction and demodulation ratio method

图6 为采用解调比法与直接重建法重建图像的斯特列尔比对照曲线。可知解调比法相较直接重建法，在光强扰动变化范围1%～15%时，图像斯特列尔比提升变化范围为0.07～0.20。

图6 解调比法与直接重建法光场成像斯特列尔比曲线Fig.6 Optical field imaging SR curve of demodulation ratio method and direct reconstructed method

表3 和表4 分别为直接重建和解调比法重建图像的峰值信噪比，可知在同样光强扰动条件下，解调比法相较直接重建法，图像峰值信噪比均有所提升，在光强扰动变化范围1%～15%时，图像峰值信噪比提升变化范围为0.26～1.1。

表3 不同强度光强扰动下直接重建图像峰值信噪比Table 3 PSNR of direct reconstructed image under different BR

表4 不同强度光强扰动下解调比法重建图像峰值信噪比Table 4 PSNR of demodulated reconstructed image under different BR

表5 和表6 分别为直接重建和解调比法重建图像的结构相似度，可知在同样光强扰动条件下，解调比法相较直接重建法，图像结构相似度均有所提升，在光强扰动变化范围1%～15%时，图像结构相似度提升变化范围为0.000 6～0.002 9。

表5 不同强度光强扰动下直接重建图像结构相似度Table 5 SSIM of direct reconstructed image under different BR

表6 不同强度光强扰动下解调比法重建图像结构相似度Table 6 SSIM of demodulated reconstructed image under different BR

综合仿真结果可得：与直接重构图像效果相比，解调比法抑制光强扰动后，重构图像轮廓清晰，图像斯特列尔比最大提升0.20，峰值信噪比最大提升1.1，结构相似度最大提升0.002 9，可有效抑制光束光强扰动对成像像质的降质影响效应。激光束光强扰动变化范围越大，解调比法抑制光强扰动后图像斯特列尔比提升越高。当光强扰动近10%时，目标边缘轮廓模糊，成像质量下降明显，在光场成像系统设计时，应保证光强扰动低于10%，若光强扰动超过10%，应采取光强扰动抑制方法，提高光场成像像质。

3.2 桌面实验验证与结果分析

在室内桌面实验平台上验证解调比法抑制光束光强扰动的像质提升效果。首先进行激光光束频谱采样，采样完毕后直接重构图像，计算图像斯特列尔比；其次在激光光束频谱采样过程中依次计算光束不同时刻解调信号比，由所提方法消除光强扰动对成像像质影响，并计算两次实验所成图像斯特列尔比，比较像质提升效果。

构建的光场成像实验平台如图7 所示，主要包括激光发射单元和光束接收单元。发射单元包括光源、声光驱动器等；接收单元包括探测器、信号解调模块等。受实验平台与实验条件限制，桌面光场成像实验系统不具备条件开展外场实验，因此开展了室内实验验证。

图7 光场成像实验平台Fig.7 Experiment platform of optical field imaging

基于解调比法抑制光束光强扰动的光场成像效果如图8 所示。图8（a）为卫星模拟目标；在光强扰动方差0.06 mW 条件下，直接重构图像如图8（b）所示，受光强扰动影响，重建图像中心圆孔无法分辨；采用解调比法消除光强扰动后的目标图像如图8（c），目标中心圆孔可分辨。图8（b）中图像斯特列尔比为0.639，峰值信噪比为57.867，结构相似度为0.991；图8（c）中解调比法处理后图像斯特列尔比为0.821，峰值信噪比为59.928，结构相似度为0.998，三个指标分别提高了0.182、2.061、0.007。

图8 光强扰动抑制前后重构图像对比Fig.8 Comparison of image reconstruction effect before and after suppression of light intensity disturbance

图8（d）为字母A 目标原始图像，图8（e）和图8（f）分别为字母A 目标在光强抖动方差0.06 mW 条件下直接重构图像和解调比法重构图像，可知解调比抑制光强扰动后得到的目标图像轮廓比直接重构图像轮廓更清晰。图8（e）的斯特列尔比为0.656，峰值信噪比为59.887，结构相似度为0.996；图8（f）的斯特列尔比为0.823，峰值信噪比为61.693，结构相似度为0.998，三个指标分别提高了0.167、1.806、0.002。

基于三光束光场成像桌面实验平台对解调比方法进行了验证，实验结果表明，在光强扰动方差0.06 mW条件下，解调比法消除光强扰动后，室内卫星模拟目标和A 目标光场成像斯特列尔比分别提升0.167 和0.182，图像峰值信噪比分别提高了2.061 和1.806，图像结构相似度分别提高了0.007 和0.002，图像清晰度明显提高。

4 结论

针对新型光场成像系统激光光束光强扰动和湍流等因素影响带来的频谱重建误差，进一步影响重构图像像质问题，本文提出了一种基于光场回波信号解调比求解算法，从原理上消除了光强扰动因子对重建方程中频谱分量迭代误差的影响，间接提高了频谱重建精度和光场成像质量。仿真结果表明解调比法抑制光强扰动后，重构图像斯特列尔比、峰值信噪比、结构相似度等指标均有所提高，解调比法可有效抑制光强扰动降质效应，提升像质。桌面实验结果表明，图像清晰度得到明显改善，三个图像像质评价指标均有所提高，进一步证明了该方法的有效性。所提解调比方法可有效抑制光束光强扰动对像质影响，降低多光束光场成像系统中各光束光强稳定性要求，可为光场成像技术的实验研究和应用转化提供技术支撑。