基于残差注意力网络的波前畸变复原方法
曹阳,张祖鹏,彭小峰
(重庆理工大学 电气与电子工程学院 重庆 400054)
0 引言
携带轨道角动量(Orbital Angular Momentum,OAM)的光束可提高系统信道容量和频谱利用率,成了众多学者的研究对象[1]。目前,在实验室条件下通过对OAM 光束复用,已经实现了Tbit/s 级别的数据传输[2]。然而在自由空间光通信(Free Space Optical Communications,FSO)系统中,大气湍流引起的大气折射率变化,使得大气传输的激光束出现振幅随机起伏以及相位扭曲,导致无线光通信系统的性能下降[3]。自适应光学(Adaptive Optics,AO)是可通过校正光束动态波前畸变来提升通信系统性能的技术,已成为无线光通信系统的研究热点[4]。AO 系统一般包括波前传感器、波前控制器和波前校正器,而根据AO 系统是否使用波前传感器可将其分为常规AO 和无波前探测AO 两类[5]。常规AO 系统在天文观测、生物医学领域取得了广泛应用,但是受到系统结构复杂性和工作原理本身的制约,其应用范围具有局限性[6]。无波前探测AO系统可直接利用探测到的光强信息设计控制算法,产生波前校正器所需要的控制信号,即根据畸变光强图像进行波前重构[7]。
经典无波前探测的波前重构方法包括Gerchberg-Saxton 相位恢复算法[8]、随机并行梯度下降算法[9]、模拟退火算法以及遗传算法[10]等,这些算法多需要通过迭代计算求解,难以实现实时的波前重构。基于深度学习(Deep Learning,DL)的无波前探测是将CCD 相机捕捉到的光强图像作为神经网络输入,将波前像差或Zernike 系数作为输出,然后再将输出转化为控制信号,最终控制变形镜实现波前校正。文献[11]中应用点扩展函数的深度学习方式实现波前重构,获得了比随机重构更低的误差,但对于较大尺寸图像的复原实时性较差。文献[12]针对现有搜索算法迭代次数过多的问题,提出基于深度神经网络的模型,从而获取Zernike 系数进行波前校正,并减少了时间开销。上述研究表明了DL 技术在AO 中可有效应用,但通常存在计算成本高的问题。为降低计算复杂度,文献[13]使用卷积神经网络模型,直接从单个光强图像估计波前Zernike 系数,通过实验验证了过曝光、离焦和散射等预处理方式的有效性。文献[14]同样使用卷积神经网络模型,使其学习畸变涡旋光强分布与前20 项Zernike 系数之间的映射关系,缩短了计算时间。这些研究表明DL 具有巨大的潜力,另有相关文献从几何光学方面提升系统性能,如文献[15]中用相位差异思想,提出将焦平面和离焦平面的光强图作为神经网络输入,并将其对应的Zernike 系数作为标签,输出波前Zernike 系数。文献[16]探讨了训练数据的一致性对波前复原性能的影响,仿真结果表明,使用单一训练数据集的模型鲁棒性不强。文献[17]同样根据相位差的思想,采集空间光调制器生成的真实相位,使用卷积神经网络建立了真实图像与其Zernike 系数的映射,并由于模型参数少,显著提升了模型的实时性。文献[18]把残差网络应用于波前重构,将远场光强图作为输入,波前Zernike 系数作为输出,验证了神经网络鲁棒性强的特性。与传统波前探测算法相比,深度卷积神经网络已经在无波前探测AO 系统上表现出了优越性,但仍然存在对光斑特征感知和表达不足的问题。随着网络不断加深,易出现梯度消失、爆炸甚至过拟合的现象,难以完成实时精确的重构任务,过多的池化操作也会导致小目标信息丢失,重构误差过大。
针对上述问题,本文引入残差网络作为主干网络,利用其跳层连接的特点,使网络学习更深层次的特征表示,并在网络中嵌入带有多尺度特征提取的混合注意力结构,利用空洞卷积来提取光斑的不同感受野信息,在扩大特征尺度的同时避免网格伪影现象;应用通道注意力加权融合不同尺度的特征,并向后传播,通过空间注意力对特征图像素间的依赖性进行聚合,得到更具分辨率的特征图;定义网络损失函数为多个指标的加权和,从而增加重构Zernike 系数的真实性。
1 涡旋光束大气传输模型
基于深度学习的无波前探测AO 系统中通常用神经网络模型代替传统校正算法,从畸变光强图像中反演出波前像差或是其Zernike 系数,结合神经网络模型的无波前探测AO 系统框架如图1 所示。空间光调制器法是常见的涡旋光束生成法之一,激光器发射的光束经过扩束准直后,入射到搭载了叉形光栅的空间光调制器上,即可生成预校正的涡旋光束。在大气传输时,光波发生波前畸变,其相位面不是平面,此时的畸变波前被分光镜分为两部分,一部分聚焦到波前校正系统,另一部分用于信息传输。波前控制器接收到波前畸变信息之后,将进行波前重构,得到波前系数,并据此生成控制电压系数,由变形镜(Deformable mirror)产生共轭波前,补偿接收到的光束,校正完后再将光束送到信息接收端。
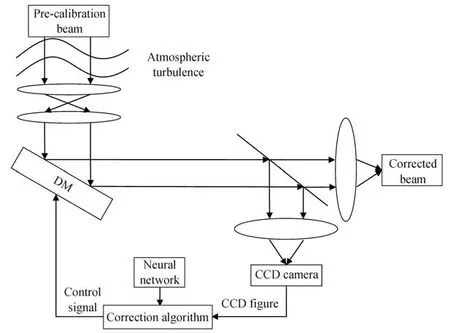
图1 无波前探测AO 系统原理Fig.1 Schematic diagram of AO system without wavefront detection
在自由空间光通信中,涡旋光束与普通光束相比,具有连续螺旋形波前,在光束传播的方向上相位具有不确定性,该处即为相位奇点。涡旋光束中拉盖尔-高斯(Laguerre-Gauss,LG)光束是一种具有代表性的光束,在自由空间下其光场分布为
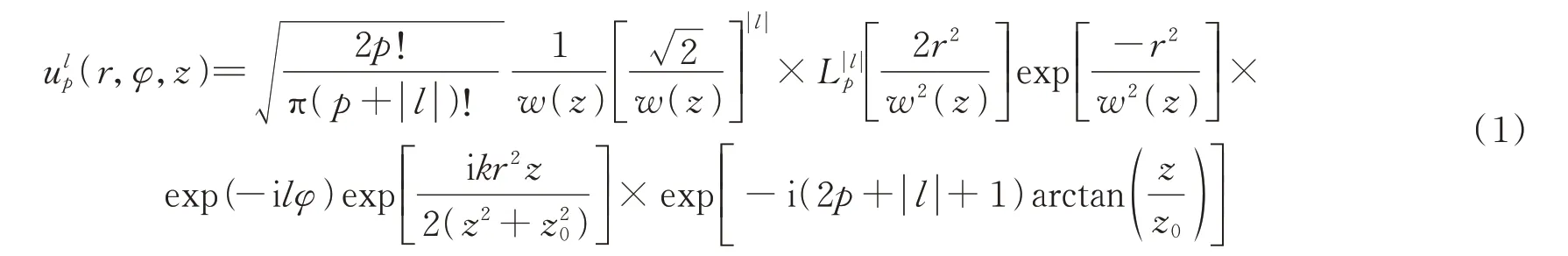
式中,l为涡旋光束的拓扑荷数,可以取为任意整数;p表示LG 光束的径向指数;r为空间点到传输轴的径向距离;φ为方位角;,w0为光束束腰半径,z0=kw0/λ为瑞利距离,k=2π/λ为波数,λ为光波长;为拉盖尔多项式。假设光束发射点位于z=0 处,且为了在研究方便的情况下不影响结果,令p=0,则发射光束光场分布表示为

根据式(2)可以模拟出LG 光束在大气湍流中的传输过程,考虑光束传输中存在衍射效应,因此经过衍射光阑后的光场分布为

式中,x-y为入射平面坐标,x1-y1为接收平面坐标,T(x,y)为圆孔光阑透过率函数,u(x,y,0)为z=0 时的光场分布,设置圆孔半径rc=w0。
当光波通过多个相位屏时,只有相位变化而振幅不变,在Rytov 近似下,可以得到传输距离为Δz时的光场分布为
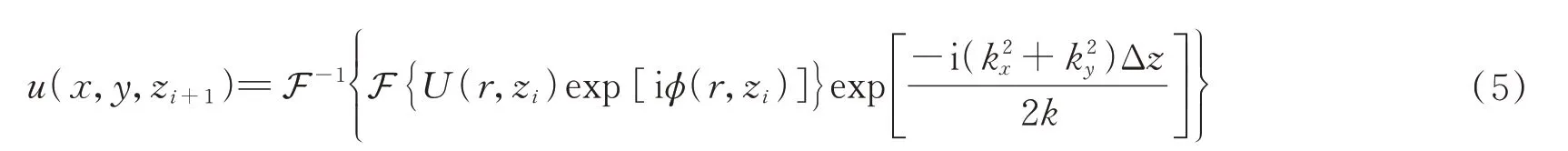
式中,F-1和F 分别表示傅里叶逆变换和傅里叶变换;ϕ(r,zi)表示大气湍流相位屏函数;kx和ky分别表示x和y方向上的空间波数,且。因此,只需模拟出大气湍流的相位屏模型就可以计算出接收端处光场的大小,选用Noll 定义的Zernike 多项式来模拟湍流相位屏ϕ(r),可表示为
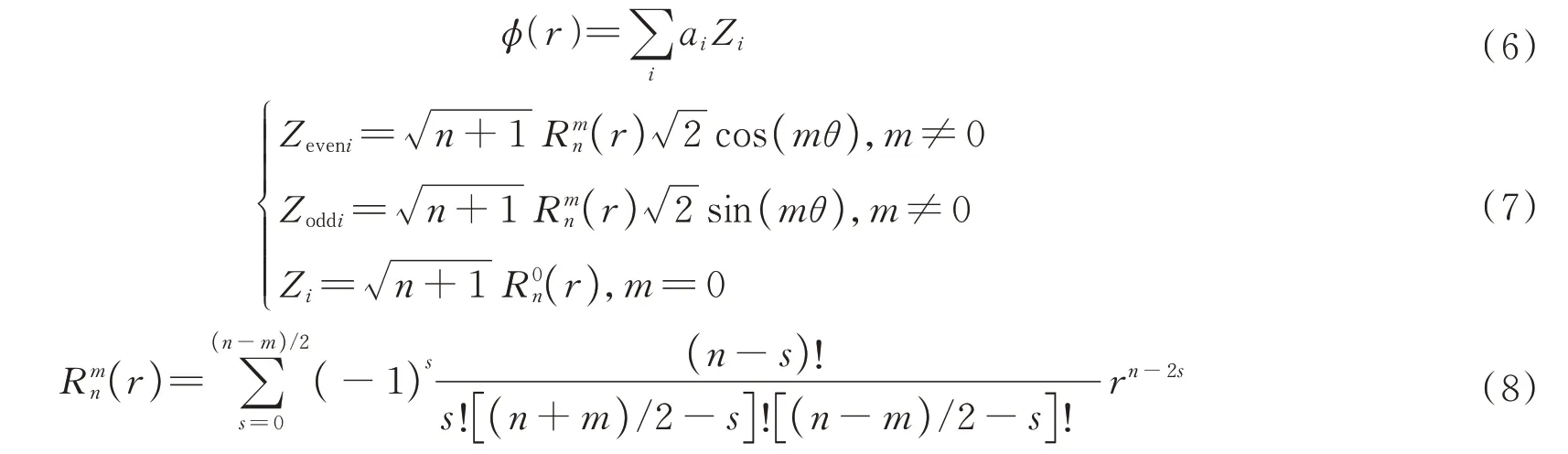
式中,Zi为第i项多项式对应不同相差,Zeveni为第偶数项,Zoddi为第奇数项,为径向函数表达式,r和θ为极坐标,n和m分别为径向和角向级次,始终是整数并且满足m≤n,n-|m|=even,even 为偶数。Zernike 多项式的第一项表示平移,对图像成像质量没有影响,更高阶的多项式可以表示更高的频率成分,因此本文不考虑第一项式,并选取36 阶的多项式生成符合实际情况的大气湍流相位屏。
2 残差注意力网络模型
2.1 残差网络模型
由于捕获到的光强图中包含波前像差信息,因此基于深度卷积神经网络的模型能够从畸变光强图中提取出波前Zernike 系数,甚至直接提取大气湍流相位,其权重共享的特性,可在减少学习参数量的同时实现实时波前重构。然而一味地增加网络深度,不仅容易过拟合,还极容易陷入局部最优,且卷积操作会由于感受野大小的不同,导致本具有联系的像素间提取出的特征存在差异,这些差异会导致重构的像差较大。针对上述问题,用残差网络的思想构建特征图的恒等映射,使得后面的层能学习到网络的残差,减少过拟合风险,并结合全局上下文信息,加入注意力机制,在特征之间建立联系,增加网络的波前重构能力。基于残差网络的波前重构系统如图2 所示。

图2 网络整体结构Fig.2 Overall network structure
骨干网络为ResNet50 模型,首先通过7×7 的下采样卷积操作将输入的光强图转变为特征图像,大尺度卷积核在尽可能保留特征信息的情况下减小计算量。之后采用过滤器大小为3×3 的最大池化操作减少特征映射的参数,将其降维至初始图像的1/4 大小。然后将混合注意力模块嵌入到ResNet 模型中,充分捕获特征信息,每个混合注意力模块包含两次卷积操作和一次混合注意力计算操作,每次卷积操作的通道数如图2 所示。最后经过全连接层将特征从三维空间映射到一维空间中,并加入Dropout 防止过拟合,最终的输出为输入光强图中波前像差对应的Zernike 系数。
2.2 混合注意力结构
为了弥补深度ResNet 感受野有限,跨通道交互缺乏,小目标信息易丢失的问题,在网络中添加空间注意力(Spatial Attention,SA)机制与动态选择机制网络(Selective Kernel Neural Networks,SKNet)[19]相结合的混合注意力结构,主要采用卷积操作提取特征映射的相关信息,加入残差跳连结构根据输入的特征的重要程度来为模型合理地分配计算资源。提出的混合注意力结构包括带有通道注意力机制(Channel Attention,CA)的SKNet 与空间注意力机制,其结构如图3 所示。

图3 混合注意力结构Fig.3 Structure diagram of mixed attention
对于光强图像中不同大小的光斑,其特征的尺度同样变化,如果采用大小相同的卷积核,小光斑特征信息的表达能力逐渐变弱,导致重构像差误差增加。针对此,用多尺度特征提取网络SKNet,使模型增强浅层特征的表达,有利于网络中较小目标的回归,让模型把注意力更加聚焦在目标本身。
SKNet 可以分为分解、融合和选择三个部分。在分解部分,选取不同大小的卷积核进行特征映射操作,虽然多分支结构能够挖掘更丰富的语义信息,增强网络的表达能力,但同时也加大了网络训练的难度。因此选用3×3 和5×5 大小的双流网络结构,表示为

式中,X∈Rh×w×C为输入的特征图,f代表卷积操作,这样不仅可以通过多分支结构获取光强图像中高低频部分的特征表示,而且可以避免过多的网络分支造成训练难以收敛。其中5×5 的卷积采用空洞卷积操作。
在融合部分,通过求和操作控制特征图相加,然后由全局平均池化统计卷积层每个通道携带的信息得到s,最后进行特征降维得到z。整体过程表示为

式中,Fgp是全局池化操作,Ffc是全连接操作,δ为线性整流函数(Rectified linear unit,relu),B 为Batch normalization 层,Ws∈Rd×C,d=max(C/τ,L)表示全连接之后的特征维度,C为通道维度大小,τ为压缩因子,L表示d的最小值。全局注意力模块用于整合深层和浅层特征,以缓解深层特征分辨率低而引起的较小光斑信息丢失的问题。
选择部分,使用softmax 函数计算各个通道的权重分布。计算方式为

式中,a和b分别为和的软注意力权重矩阵,ac为a的第c行元素,bc同理。A和B同为注意力权重矩阵,Ac为A的第c行元素,Bc同理。由于池化层的存在,高频信息量会进一步减少,导致深层特征对小目标的表达能力较弱。引入空间注意力机制对目标区域的特征加以权重,寻找网络中特征间的联系,使特征提取网络有选择性地关注包含重要信息的目标区域。最后的输出矩阵计算公式为
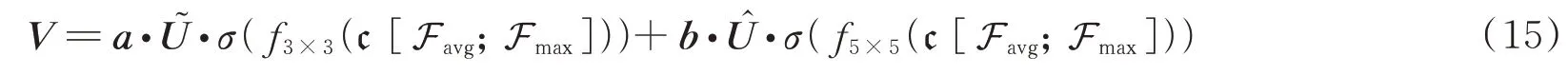
式中,c表示拼接操作,σ为sigmoid 激活函数,Favg与Fmax分别表示沿着通道轴执行的平均池化操作和最大池化操作。与通道注意力不同的是,空间注意力可以将高低频信息区分开来,这与通道注意力是互补的[20],经过优化空间信息的特征图可以有效表达像素点间的特征相似度,空间注意力可以很好地获得上下文语义信息。
2.3 损失函数
为了让波前像差的Zernike 系数重建更合理,结合常用的波前评价指标来改进网络的损失函数。常用的AO 系统评价指标有波前峰谷值(Peak to Valley,PV)和波前均方根值(Root Mean Square,RMS)等,PV 用来表示波前最高点与最低点的差值,RMS 表征被测光束波前相较于理想波前的偏离程度[21],其公式分别为

式中,Δϕ为波前像差,为其均值,ρ和θ为光瞳面的极坐标。可以看出,PV 值反映的波前信息不够全面,RMS 值则更注重波前的整体信息,结合两者能更准确地表现波前情况。因此结合均方误差(Mean Squared Error,MSE)的损失函数为

式中,zact和zpre分别为实际与估计的Zernike 系数,长度为N,γ为各损失的权重,L 为各个损失函数的加权和,损失函数的缩小代表着重构精度的提高。
3 基于深度学习的波前复原模拟
3.1 仿真验证
为验证提出的残差注意力网络的可行性,模拟涡旋光束在不同湍流强度下的传输,展开波前复原仿真。根据Taylor 冻结湍流假设理论,大气湍流在短时间内其空间结构保持不变,因此假设湍流冻结时间为10~20 ms。涡旋光束在经过大气湍流之后发生了相位失真,其大小与D/r0比值相关,其中D是系统孔径直径,r0是大气相干长度。采用大气相干长度r0表述湍流强度的影响,r0越大表示湍流强度越小。对于光束束腰半径为3 cm 的系统,D/r0=2 可以表示弱湍流,D/r0=10 可以表示中湍流,D/r0=20 可以表示强湍流。其余参数设置如表1 所示。

表1 仿真参数Table 1 Parameter of simulation
同时为使仿真更加合理,设置比值范围为D/r0=2~20,间隔为2,每个比值生成5 000 组随机Zernike 系数和对应的光强图作为训练数据,其中训练集、验证集与测试集的比值为8∶1∶1,训练图像的大小调整为224×224 像素,网络的输出为36 位Zernike 系数。为使实验对比更清晰,将从输出的Zernike 系数中生成对应的波前相位进行对比,并从预测相位与真实相位之间的残差来测试网络准确性。由式(3)、(5)和表1 中参数可生成如图4 所示的湍流相位屏和光强分布。图4(a)为弱湍流强度下Zernike 系数模拟的湍流相位屏,单位为度(°),以及拓扑荷数为3 的LG 光束经过圆孔光阑后的光强分布,图中PV 值和RMS 值的单位为rad,其值较小,代表大气环境良好。图4(b)~(c)为中湍流和强湍流下的相位屏图和光强图,随着PV 值和RMS 值变大,相位屏的起伏变大,表示大气信道环境变差,光强分布发生畸变。

图4 湍流相位分布和光强分布Fig.4 Turbulent phase distribution and light intensity distribution
仿真环境采用python 语言的keras 深度学习库,离线训练迭代次数epoch 设为100,每个批次大小Batchsize 设为50。采用自适应学习率Adam 算法,设置初始学习率为0.001,当网络精确度在10 个批次内未增加时学习率下降为0.000 1,在全连接层中使用Dropout 层来防止网络过拟合,并使用tanh 函数作为网络激活函数。综合评估后损失函数各个部分的权重设置为γMSE=1,γPV=0.8,γRMS=0.5。训练过程中的损失函数值与准确率大小如图5 所示,图5(a)中损失函数随着迭代次数增加而减小,图5(b)中准确率逐渐增加,最终整体准确率能达到97%左右。

图5 模型的损失函数与精确度Fig.5 Loss function and accuracy of the model
为验证残差注意力网络模型的有效性和鲁棒性,仿真中在不同湍流强度下随机生成了5 组Zernike 系数,并生成对应的相位屏如图6(a)所示。通过提出的混合注意力网络模型预测Zernike 系数,估计的结果和其残差相位如图6(b)~(c)所示,文献[12]的结果如图6(d)所示。可以看出提出的残差注意力网络模型预测的残差最小,仅使用卷积神经网络的模型预测的结果不够准确,其残差相位的PV、RMS 值如表2 所示,本文方法预测的畸变相位残差值较小,相较于之前的工作能得到更符合实际的相位屏。因此从图6 和表2 可知,在不同湍流强度下混合注意力网络均有很好的重构效果,且复原的相位屏与实际相位屏相似度高。图7 为5 种不同湍流强度下预测的Zernike 系数与实际系数的对比,可以看出本文方法的预测结果与实际系数较为接近。
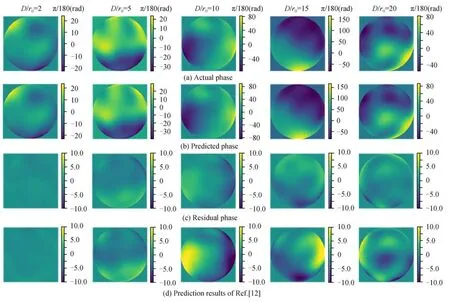
图6 预测的湍流相位与实际对比Fig.6 Comparison of the predicted turbulence phase with the actual phase

表2 不同湍流强度下残差相位的PV 值和RMS 值Table 2 PV and RMS values of the residual phase at different turbulence intensities
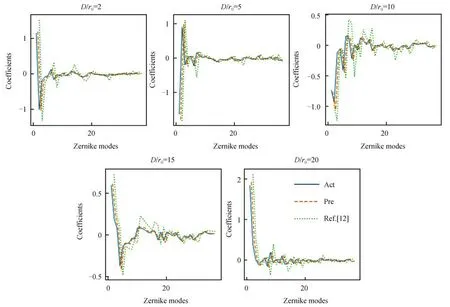
图7 预测的Zernike 系数与实际对比Fig.7 Comparison of the predicted Zernike coefficient with the actual coefficient
根据预测的Zernike 系数重构波前之后,向畸变光束加载反相波前,即可实现湍流相位的校正。为验证残差注意力网络模型的鲁棒性,在不同信噪比下进行仿真。不同信噪比下的光强如图8 所示,随着湍流强度增加,LG 光束的轮廓逐渐变形,噪点分布也随着信噪比减小而增加。预测的结果如图9 所示,在高信噪比条件下预测效果与无噪声相近,在低信噪比,如5 dB 的情况下,残差相位的起伏仍比较平缓,具体结果如表3所示。通过表3 和图9 的结果可知,提出的混合注意力网络能重建准确的波前相位,并具有较高的鲁棒性。

表3 不同信噪比下残差相位的PV 值和RMS 值Table 3 PV and RMS values of the residual phase at different SNR

图8 不同信噪比下的光强Fig.8 Light intensity map at different SNR

图9 不同信噪比下的残差相位Fig.9 Residual phase at different SNR
3.2 消融仿真
为验证提出的混合注意力结构的有效性,仿真中训练了几种不同模型,包括基础骨干网络ResNet50、添加CA 的网络、添加SA 的网络以及添加混合注意力结构的网络,得到了如表4 所示的准确率结果。

表4 不同模型的准确率与计算时间对比Table 4 Comparison of accuracy and calculation time of different models
表4 表明,添加了注意力机制的网络在重构Zernike 系数上的精度最高,且与单一注意力结构相比,混合注意力结构的准确率更高,达到了97.1%。在运行时间上,测试了1 000 次后取其平均值,从表中可知,添加注意力网络的计算时间均在10 ms 以下,可以满足实时波前校正的要求,随着硬件性能的增加,运行时间可以继续降低。混合注意力结构的运行时间比ResNet50 稍长,但综合准确率来评估后,本文提出的残差注意力网络性能最好。
为验证注意力机制在网络中的作用,在原数据集的基础上,设计以下消融仿真,将提出的混合注意力机制作为基础训练模型,然后分别移除CA 和SA 训练得到2 个不同模型,训练中所有参数设置均相同。在相同湍流条件下随机生成一个相位屏,其结果如图10(a)所示,不同模型测试的结果如图10(b)所示。图10(c)左图为完整模型复原的波前残差,相较于单一注意力机制得到的结果,其重构相似度最高。从图10(c)中可知,移除CA 会导致特征之间的关联性下降,重构波前的相似度变低,移除SA 导致特征提取能力下降,特征表达的能力变弱。该消融实验得到的评价指标对比如表5 所示,完整模型的残差PV 值为0.145 1 rad,RMS值为0.052 7 rad,相比其他两种模型更小。综上,混合注意力机制具有实际有效性。
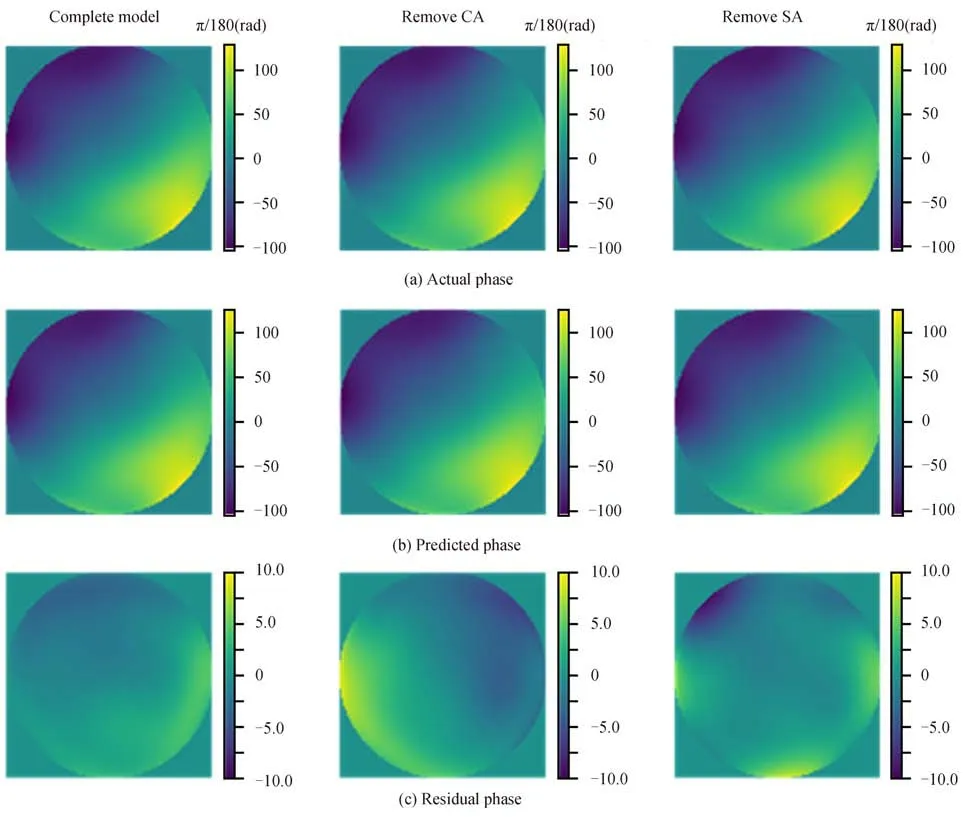
图10 去除部分注意力机制与完整模型的预测结果对比Fig.10 Comparison of prediction results between the model with partial attention mechanism removed and the complete model

表5 去除部分注意力机制的评价指数对比Table 5 Comparison of evaluation indexes of removing partial attention mechanism
为验证各种损失函数在模型中的作用,在原数据集上进行消融仿真。完整模型为联合3 种损失函数的网络,分别移除其中一种损失函数训练不同模型进行测试,训练中所有参数的设置均相同。在相同湍流条件下随机生成一个相位屏,结果如图11(a)~(c)所示,不同模型测试的结果如图11(b)所示。完整模型复原的波前残差如图11(c)左图所示,可以看出,移除PV 时,得到的波前残差畸变幅度较大;移除RMS 时,波前残差结果在内容上发生了失真,导致整体相似度较低。各个模型生成的评价指标对比如表6 所示,完整模型的残差PV 值为0.164 9 rad,RMS 值为0.039 5 rad,因此结合实际评价指标的损失函数是合理有效的。

表6 去除部分损失函数的评价指数对比Table 6 Comparison of evaluation indexes of partial loss function

图11 去除部分损失函数的模型与完整模型的预测结果对比Fig.11 Comparison of partial loss function with complete model
4 结论
本文针对大气湍流引起涡旋光束畸变,导致FSO 通信质量降低的问题,提出了结合残差注意力网络的AO 系统反演波前相位,从而实现有效的波前校正。训练后的模型建立了前36 阶Zernike 系数与畸变光强分布之间的准确映射关系。在不同湍流条件下进行仿真,得到的波前残差PV 值和RMS 值优于现有研究,表明网络具有强鲁棒性。在D/r0=2 的情况下PV=0.045 rad,RMS=0.011 rad;在D/r0=10 的情况下PV=0.226 rad,RMS=0.046 rad;在D/r0=20 的情况下PV=0.275 rad,RMS=0.071 rad。预测的Zernike 系数与实际系数相近,通过系数重构的相位与实际相位相似度高。验证了混合注意力网络在重构波前相位任务中的有效性,在较少增加时间复杂度的情况下准确率达到最高。残差注意力网络精确度高、实时性好和灵活性强的特点,可为深度学习在AO 系统中的实际应用提供保障。

