动平台光学测量设备跟踪性能检测技术
李希宇,高昕,孙亮亮,雷呈强,师恒,2,3,4,胡蕾,宗永红,郑东昊
(1 北京跟踪与通信技术研究所,北京 100094)
(2 中国科学院西安光学精密机械研究所,西安 710119)
(3 中国科学院空间精密测量技术重点实验室,西安 710119)
(4 青岛海洋科学与技术国家实验室发展中心,山东 青岛 266237)
0 引言
随着光学测量技术及靶场需求的不断发展,固定基座的光学测量设备已经不能满足现代靶场的要求[1],海上和陆地机动式测量的需求越来越高,光学测量设备从陆基逐渐扩展到船载[2]、车载[3]和机载[4]等动机座平台,动平台光学测量设备扩大了可探测距离,具有机动性强、应用范围广等优点。
动平台在运动过程中会产生横移、纵移、升降、横摇、纵摇、偏航6 个自由度的平动和转动运动特性[5],其中横移、纵移、升沉为3 个方向位移量变化,横摇、纵摇、偏航为3 个方向角度转动变化量。同时,光学测量设备观测的典型机动目标一般也存在六自由度(Degree of Freedom,DOF)的运动特性,因此需要采用六自由度的检测靶标,用于实现在地基条件下完全真实模拟动平台与典型机动目标的各个运动特性。
现阶段对动平台光学测量设备跟踪性能的检测均沿用传统地基检测装置,由于传统地基检测装置无法真实模拟动平台的运动特性,因此无法在研制阶段考核实际应用环境中的跟踪性能。此外,地基检测装置普遍使用单轴光学动态靶标[6-8],其在空间上属于单自由度旋转靶标,工作时仅由速度反馈回路控制调节旋转轴的旋转速度,模拟出近似正弦运动轨迹的机动目标,这种模拟目标与真实机动目标在运动特性上存在较大的差别,主要表现在运动轨迹单一,且运动方程在方位和俯仰方向上的分量具有高阶导数。虽然目前检测靶标的自由度数提高到了3 个[9],但其在工作空间中仍存在位置盲点,且在运动过程中会出现运动奇异性的问题。
综上,采用目前地基检测装置对动平台光学测量设备进行跟踪性能检测时,不能完成真实环境下跟踪性能的检测与考核评价,极易导致设备带有遗留问题参加试验任务,在任务中一旦发现设备跟踪性能达不到要求时,设备的整改难度大且研制周期与成本会大幅增加。
针对上述技术问题,为了工程上实现在地基条件下动平台光学测量设备跟踪性能的检测,将模拟光学目标安装在六自由度机械臂末端构建了新型六自由度检测靶标。鉴于传统的多自由度串联机构运动学建模与轨迹规划方法,如DH(Denavit Hartenberg)[10]、M-DH(Modified-Denavit Hartenberg)[11]和CPC(Complete and Parametrically Continuous)[12]等,需要建立6 个坐标系,计算过程繁琐,存在实时性差、易出现运动奇异解等问题。本文采用旋量指数积方法[13]只建立了检测靶标首尾两个坐标系,可完成连续无奇异性的运动学建模,且能完整表达各个关节之间的转换关系,运算高效,求解运动学逆解方便,可实现动平台和典型机动目标实时高精度的运动轨迹规划。基于搭建的新型六自由度检测系统,制定合理可行的检测方法,实现在地基条件下对船载动平台光学测量设备的跟踪性能检测与鉴定试验。
1 检测系统构建
为实现地基条件下动平台光学测量设备跟踪性能的检测与鉴定,检测系统主要由平行光管、六自由度机械臂、操作控制分系统、数据通信分系统、时统终端和数据处理分系统等组成。检测系统组成如图1所示。

图1 检测系统组成示意图Fig.1 Composition diagram of detection system
检测系统的检测靶标由六自由度机械臂和平行光管组成。其中机械臂用于真实模拟动平台和典型机动目标的实时运动轨迹,由基座、腰部、下臂、上臂、腕部以及手部6 个关节串联组成,其中手部末端安装平行光管,前3 个关节用于引导平行光管至给定的空间位置,后3 个关节用来决定平行光管的姿态角度。六自由度检测靶标解决了现有靶标存在的运动特性不足的问题,具备工作空间任意位置高精度定位、占用空间小和灵活安装等优点。
平行光管安装于机械臂手部末端,作用是将模拟光学目标投影至无穷远位置,消除检测过程光学测量设备变焦产生的误差。为保证测试过程中光学测量设备的进光量,根据光学系统指标,设计了合适的光学视场与之匹配。操作控制分系统依据不同任务类型,通过运动控制卡以及控制算法,根据动平台与典型机动目标的融合运动轨迹数据,规划并计算控制指令,通过驱动器实现对检测靶标的高精度运动控制。
由数据处理分系统、时统终端和数据通信分系统组成电控舱。数据处理分系统需将滤波后的动平台与典型机动目标的融合运动轨迹发送给操作控制分系统,此外数据处理分系统接收光学测量设备跟踪目标图像、跟踪脱靶量等其他检测数据,对跟踪性能进行计算与评价。时统终端主要为检测靶标和光学测量设备提供统一的时间基准,确保两者数据交互的一致性。数据通信分系统主要完成操作控制分系统、数据处理分系统、检测靶标和光学测量设备数据接口四者之间的数据通信。
2 检测靶标轨迹规划算法
为了提高检测靶标轨迹规划的实时性,降低检测系统数据时延造成的跟踪误差,同时避免传统建模方法繁琐且存在运动奇异性的问题,采用旋量指数积方法建立检测靶标首尾两个坐标系,提高运算效率,以全局的方式建立连续无奇异性的运动学模型,为实时高精度模拟动平台和典型机动目标的运动轨迹奠定基础。
图2 为六自由度串联检测靶标与光学测量设备坐标系及关节参数示意图,依据旋量理论分别在检测靶标首尾建立惯性坐标系(OS-XSYSZS)和工具坐标系(OT-XTYTZT)。其中惯性坐标系的原点OS与地面固定连接,YS轴正向指向光学测量设备,ZS为过原点的铅垂线,向上为正,XS与YS、ZS构成右手直角坐标系。工具坐标系的原点OT定义在第4、第5 与第6 轴线的交点处,XT、YT和ZT三个轴的正向与惯性坐标系相同。为了便于解算检测靶标末端模拟目标相对于光学测量设备的空间位置,在光学测量设备安装位置建立测量坐标系(OM-XMYMZM),其原点OM位于光学测量设备与地面连接处,XM、YM和ZM三个轴的正向与惯性坐标系相同。

图2 检测靶标坐标系及关节参数示意图Fig.2 Coordinate system and link parameters diagram of detection target
检测靶标的每个轴均可看作为旋转关节,根据欧拉定理,对于各个轴的每一个旋转运动,均有一个旋转矩阵R(R∈SO(3))与之对应,SO(3)为特殊正交群,设ω是旋转轴转动方向的3×1 单位矢量,θ为转动角度,则R可写成
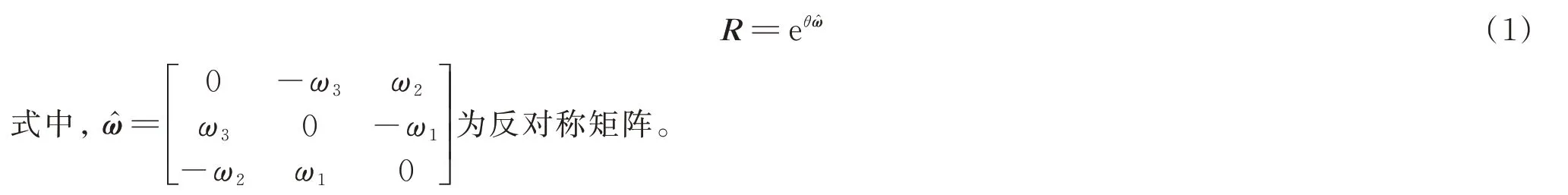

式中,E为4×4 阶单位矩阵,设r为旋转轴上的一点的3×1 矢量坐标,引入两个矩阵

式中,ν=r×ω;为运动旋量,是4×4 阶矩阵;ξ为的旋量坐标,是6×1 阶矩阵。
根据Chasles 定理[14],任意刚体运动都可以通过螺旋运动即绕某轴的转动与沿该轴移动的复合运动实现。因此旋转轴的运动变换可用旋量指数积形式表示为

给定各关节轴线的单位运动旋量坐标ξi来表示各关节的螺旋运动,若gST(0)表示检测靶标初始位形时相对于惯性坐标系的刚体变换矩阵,在其它关节保持不动,只转动第i关节时,第i关节的相对于惯性坐标系的位形为

由于检测靶标具有6 个转动关节,因此当6 个关节均转动时,检测靶标的运动学模型可表示为
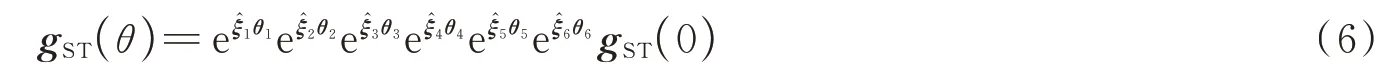
式中,gST(θ)为任意给定各关节旋转角度时,检测靶标惯性坐标系与工具坐标系之间的刚体变换。
六自由度检测靶标需真实模拟动平台与典型机动目标各个时刻的融合运动轨迹,动平台与典型机动目标均具有6 个自由度的运动特性,其中3 个是位移量变化,3 个为角度转动变化量。在实际应用中,动平台光学测量设备主要观测远距离典型机动目标,因此在光学视场中机动目标可看作无穷远的点目标,由此可忽略不计典型机动目标的3 个方向的角度转动变化量。同理,动平台3 个方向的位移量变化在光学测量设备观测远距离目标时可忽略不计。综上分析,将动平台3 个角度转动量与典型机动目标的3 个位移量的实时变化值进行融合解算,从而得到检测靶标各个时刻对应的关节转角。
图2 中各个关节的位姿即为检测靶标各关节初始角度的位姿,则初始位形表示为
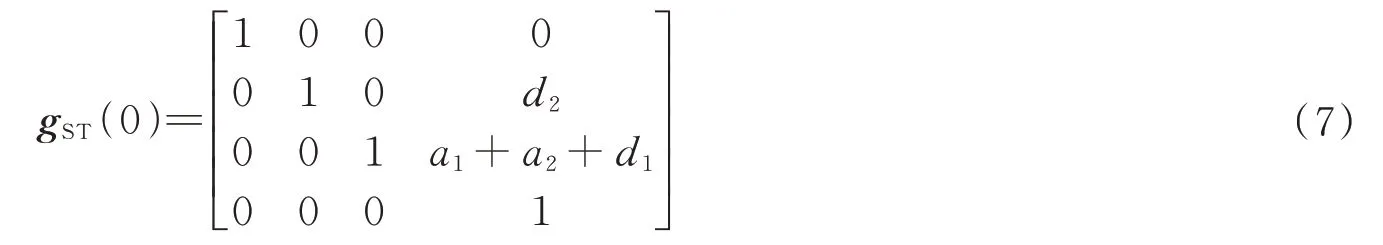
选取各关节轴线上的点坐标并计算单位运动旋量,即
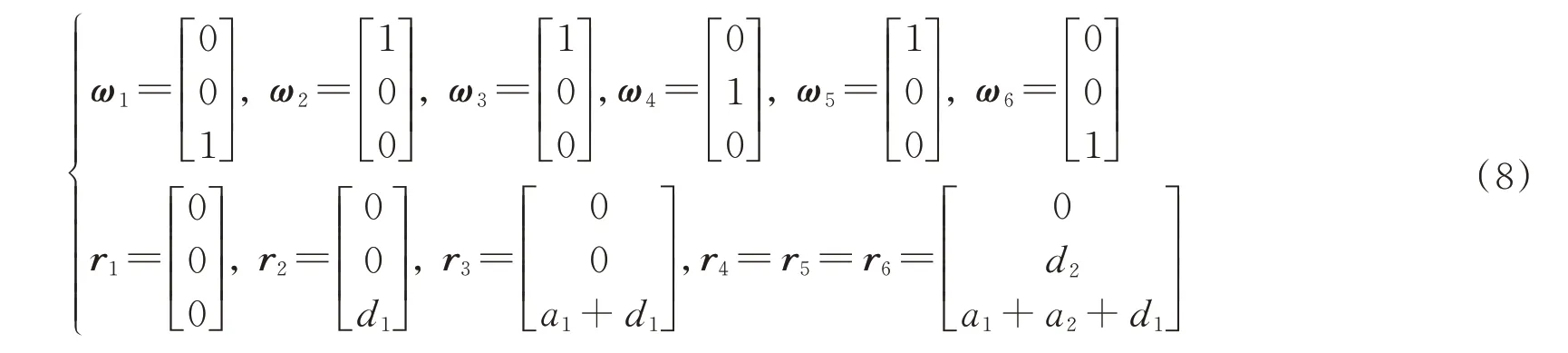
将式(8)代入式(3)和(4)中即可计算得到运动旋量矩阵,即

式中,si表示sinθi,ci表示cosθi。将式(7)和(9)代入式(6)即可得到检测靶标的运动学模型,根据运动学模型可真实模拟动平台和典型机动目标各个时刻的运动轨迹。
为了获取检测靶标末端模拟目标在光学测量设备中的空间位置,假设ti时刻模拟目标在工具坐标系下的空间坐标为(xT(ti),yT(ti),zT(ti))T,测量坐标系原点在工具坐标系中的坐标为(x0,y0,z0)T,两坐标系之间的平移与旋转矩阵记为Θ,则ti时刻模拟目标在测量坐标系下的空间位置(xm,ym,zm)T可表示为

将式(10)中模拟目标在测量坐标系中的空间位置转化为对应的极坐标系,则可以计算得到光学测量设备跟踪模拟目标时ti时刻的方位与俯仰给定理想角度值,即

3 检测方法制定及跟踪性能分析
3.1 检测方法制定
结合新型六自由度检测系统与动平台光学测量设备的特点,制定合理可行的跟踪性能检测方法,实现地基条件下对动平台光学测量设备跟踪性能的检测与鉴定,检测方法为:
1)检测之前,将与光学测量设备匹配的平行光管安装在机械臂的末端组成六自由度检测靶标,根据光学系统与检测环境,将光学测量设备以一定的距离固定在地面上,转动设备使得平行光管的模拟目标与光学测量设备光轴对齐,进入光学视场内。
2)数据处理分系统将船体动平台3 个方向的角度转动变化量与典型机动目标3 个方向的位移量变化进行融合解算,得到检测靶标各个时刻对应的关节转角,采用轨迹规划算法快速高效建立检测靶标的运动学模型,实时高精度模拟动平台和典型机动目标各个时刻的运动轨迹。将运动轨迹通过坐标转换即可获得在测量坐标系下模拟目标在光轴中心处的方位与俯仰角度值,将该实时角度值及对应的角速度值作为给定的理想输入量。
3)操作控制分系统控制检测靶标完成往复高精度轨迹运动,光学测量设备自动跟踪模拟目标,数据处理分系统接收光学测量设备跟踪目标的图像、跟踪脱靶量等其他检测数据,将跟踪脱靶量换算为方位与俯仰实际跟踪角度及对应的角速度,即可得到光学测量设备方位与俯仰角度及角速度自动跟踪曲线,同时记录各个时刻的跟踪误差数据(ΔA(ti),ΔE(ti))。
4)采用最小二乘法拟合误差曲线的包络线(ΔA'(ti),ΔE'(ti)),此时跟踪误差数据与误差曲线包络线的标准差即为设备跟踪随机误差,计算公式为

式中,(σA,σE)分别为光学测量设备方位与俯仰跟踪随机误差,N为数据个数;(ΔA(ti),ΔE(ti))分别为第i时刻的方位与俯仰跟踪误差;(ΔA'(ti),ΔE'(ti))分别为方位与俯仰跟踪误差在第i时刻的包络值。
3.2 跟踪性能分析
在检测过程中,光学测量设备跟踪性能的影响因素主要包括两个方面:检测靶标的定位精度和光学测量设备自身的跟踪性能。
3.2.1 检测靶标定位误差
六自由度检测靶标的重复定位精度为0.1 mm,由于其工作范围为1.2~2.8 m,通过角量换算可计算得到检测靶标对跟踪性能最大影响值为17.18″,即
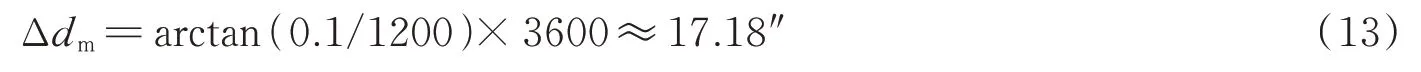
式中,Δdm为检测靶标定位误差。
3.2.2 光学测量设备跟踪性能
船载光学测量设备是典型意义上的船体动平台设备,针对某舰船的XX-1109 光学测量设备进行跟踪性能检测,该设备的跟踪性能影响因素主要包括跟踪架的测角误差Δdg、图像处理误差Δdt。其中跟踪架的测角误差受静态误差、动态增量误差和动态指向误差的影响;图像处理误差受像元分辨率误差、空间量化误差、信号处理误差、视轴调整误差和目标运动引起的误差等因素影响。
本检测系统中光学测量设备的跟踪随机误差估算公式为

根据该光学测量设备性能指标及相关试验结果,跟踪架方位和俯仰轴的测角误差分别为2.39″和2.25″。根据XX-1109 光学系统选用的探测器的技术指标和光学系统参数,可以计算得到像元分辨率误差、空间量化误差和信号处理误差(按照0.5 个像元来计算)的数值分别为8.95″、8.95″和4.475″,目标运动引起的误差按照1 个像元估算为8.95″,通过对光学系统进行标定得到视轴晃动误差为3″,通过对上述几项误差求均方根可估算得到图像处理误差为16.41″。因此根据式(14)可预估检测系统检测该船载光学测量设备方位与俯仰轴的跟踪随机误差分别为23.88″和23.86″。
4 试验验证及结果分析
4.1 跟踪性能检测试验平台
为了验证动平台光学测量设备检测系统及检测方法的有效性与优越性,搭建了如图3 所示的检测系统,并进行了在地基条件下对动平台光学测量设备跟踪性能的检测与鉴定。其中,检测靶标采用ABB 六自由度机械臂IRB 6700-205,其重复定位精度为0.1 mm。被检测设备为某舰船XX-1109 光学测量设备,其布设在距离检测靶标约5 m 的位置,检测靶标实时模拟运动轨迹,XX-1109 光学测量设备实时跟踪模拟目标从而实现对跟踪性能的检测与鉴定。

图3 跟踪性能检测试验平台Fig.3 Tracking performance detection test platform
4.2 检测靶标的轨迹规划
以某舰船的XX-1109 光学测量设备和所观测的某远距离典型机动目标为研究对象,将船体动平台3 个方向的角度转动变化量与典型机动目标3 个方向的位移量变化进行融合解算,得到检测靶标各个时刻对应的关节转角,再采用检测靶标轨迹规划算法仿真得到模拟光学目标的往复运动弧段,模拟得到的真实轨迹如图4 所示。

图4 检测靶标末端的空间运动轨迹Fig.4 The spatial motion trajectory at the end of the detection target
六自由度检测靶标高精度模拟船体动平台与典型机动目标的实时融合运动轨迹如图5 所示,其中有3个方向的角度转动变化量,即船体动平台的航向角、纵摇角和横摇角。还包括3 个方向的位移量变化,即典型机动目标的X,Y,Z三个方向的位移变化量。模拟某型号弹体机动目标在飞行中段的相对轨迹数据,根据模拟目标与光学测量坐标系之间的关系,弹体机动目标在飞行中段过程中的高度基本保持不变,因此在Z方向的位移变化量较小,而在X和Y方向的位移量变化较大。
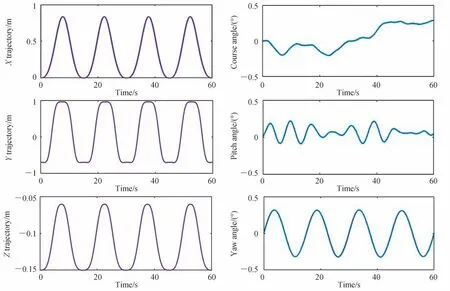
图5 检测靶标六自由度运动轨迹Fig.5 The 6-DOF motion trajectory of the detection target
由图4 与图5 可知,六自由度检测靶标末端的光学目标可真实模拟船体动平台与典型机动目标的融合运动轨迹,因此检测靶标可实现在地基条件下对船载动平台光学测量设备跟踪性能的指标检测与试验鉴定。
4.3 跟踪试验及结果分析
依据六自由度检测靶标真实模拟船体动平台与典型机动目标的实时融合运动轨迹,通过式(10)与(11)的坐标转换,即可获得测量坐标系下模拟目标在光轴中心处的方位与俯仰角度值,将该实时角度值及对应的角速度值作为给定的理想输入量。光学测量设备自动跟踪模拟目标,数据处理分系统接收光学测量设备跟踪目标的图像、跟踪脱靶量等其他检测数据,将跟踪脱靶量换算为方位与俯仰实际跟踪角度及对应的角速度,即可得到光学测量设备方位(A)与俯仰(E)角度和角速度自动跟踪曲线如图6 所示。图中红色实线表示检测靶标真实模拟船体动平台与典型机动目标的实时融合角度及角速度运动轨迹曲线,蓝色虚线为光学测量设备方位与俯仰实际跟踪角度及角速度的变化曲线。
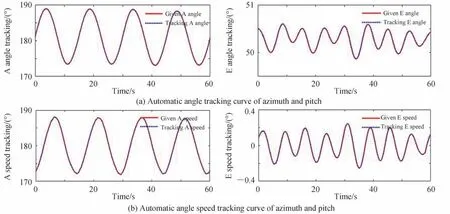
图6 方位与俯仰自动跟踪曲线Fig.6 Automatic tracking curve of azimuth and pitch
光学测量设备方位与俯仰自动跟踪角度和角速度的误差曲线如图7 所示。由于实时融合运动轨迹呈现周期性变化,方位与俯仰轴的角度与角速度跟踪曲线也呈现相同周期性的变化趋势。在角速度和角加速度处于较大的位置时,角速度和角度的误差也相应增大,因此误差曲线也呈周期性的变化趋势。
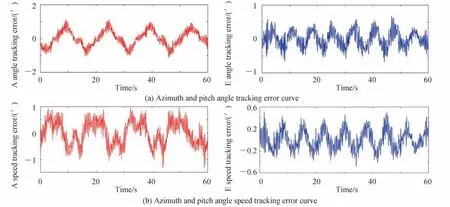
图7 方位与俯仰跟踪误差曲线Fig.7 Azimuth and pitch tracking error curve
图7 中方位与俯仰轴跟踪误差的最大值及跟踪随机误差如表1 所示。

表1 方位与俯仰跟踪误差数值Table 1 Azimuth and pitch tracking errors value
由试验数据可得出:
1)采用旋量指数积方法建立的检测靶标的运动学模型,实现了对船体动平台与典型机动目标的实时高精度运动轨迹规划,提高了运算效率,避免了传统建模方法中运动奇异性的问题。
2)由于方位轴的跟踪角速度大于俯仰轴,因此方位轴的角度与角速度跟踪误差最大值及随机误差均大于俯仰轴,在考虑角速度大小以及误差随机性等因素情况下,方位与俯仰轴的跟踪随机误差与理论分析的数值基本保持一致,从而验证了提出的动平台光学测量设备检测系统及检测方法的有效性与正确性。
3)基于搭建的新型六自由度检测系统,实现了地基条件下动平台光学测量设备跟踪性能的指标检测。
5 结论
为了在工程上实现地基条件下检测动平台光学测量设备跟踪性能指标,本文将模拟光学目标安装在六自由度机械臂末端构建了新型六自由度检测靶标,采用旋量指数积方法建立了检测靶标的运动学模型并实现了动平台和典型机动目标的高精度轨迹规划。依据检测靶标与光学测量设备的性能指标,计算并分析得到某船载光学测量设备方位与俯仰轴的跟踪随机误差分别为23.88″和23.86″。最后基于搭建的六自由度检测系统,制定了合理可行的检测方法并进行了船载光学测量设备跟踪性能的检测与鉴定试验。试验结果表明:考虑到方位与俯仰轴角速度不同的因素,船载动平台光学测量设备跟踪随机误差与理论分析基本保持一致,验证了本文提出的动平台光学测量设备检测系统及检测方法的有效性与优越性,实现了地基条件下对动平台光学测量设备跟踪性能的检测。用该六自由度动平台光学测量设备检测系统及检测方法,已成功完成了多台套船载、车载以及机载动平台光学测量设备在地基条件下跟踪性能的检测与鉴定,不仅能在设备研制阶段及时发现跟踪性能的问题与不足,还能减少设备的研发周期,降低研制成本,确保动平台光学测量设备快速形成实战能力。

