面向短距光互连的隐藏层拓展循环神经网络均衡器

刘曹洋，孙林，肖家旺，毛邦宁，刘宁

（1 苏州大学 电子信息学院，江苏省新型光纤技术与通信网络工程研究中心，江苏 苏州 215006）

（2 中国计量大学 光学与电子科技学院，杭州 310018）

0 引言

随着大数据、物联网和人工智能的蓬勃发展，基于云的互联网流量出现了爆炸式增长，这对数据中心的容量及其光互连系统的速率提出了更高的要求。同时5G/物联网等业务推动了边缘计算和云-边协同需求的发展，催生出更多边缘数据中心间的通信流量，从而将数据中心光互连系统的互连长度需求从百米延伸至10～20 km。对于高速短距离的数据中心光互连系统，光强度调制/直接检测（Intensity Modulation/Direct Detection，IM/DD）系统因其结构简单、成本低廉而被认为是最有前途的解决方案之一［1］。同时为了降低光学和电子元件的波特率和带宽要求，先进调制格式引起了人们的关注和研究，如脉冲振幅调制［2-3］、离散多音调制［4］和无载波振幅相位调制［5］。考虑到系统实现和功耗，四电平脉冲振幅调制（Four-level Pulse Amplitude Modulation，PAM-4）是一种针对100 Gb/s、200 Gb/s 和400 Gb/s 短距离光纤传输的理想调制格式［6］。与光相干检测系统不同的是，IM/DD 系统中的平方律检测会丢失信号的相位信息使得色散带来非线性的损伤难以进行补偿［7］，同时低成本激光器的啁啾以及带宽受限器件的非理想响应也会带来严重的非线性，从而限制IM/DD 系统的传输容量和距离。因此，迫切需要强大的均衡器来补偿IM/DD 系统的非线性失真。

非线性机器学习模型，特别是神经网络（Neural Network，NN）模型，由于具备高度的非线性特性被广泛用于光通信中相干系统［8-9］和IM/DD 系统［10-15］的非线性补偿。YI Lilin 等［10］提出一种前馈神经网络均衡器（Feedforward Neural Network Equalizer，FNNE）用于补偿IM/DD 系统中的强非线性损伤，其与前馈均衡器、沃尔泰拉非线性均衡器相比表现出更强的均衡性能，但同时也带来更高的复杂度。除了FNNE 之外，径向基函数神经网络均衡器［12］、卷积神经网络均衡器［13］和循环神经网络均衡器（Recurrent Neural Network Equalizer，RNNE）［14］都已在不同的场景中使用和验证。XU Zhaopeng 等［15］在50 Gbps 20 km 的IM/DD 系统中对比了具有相同输入和隐藏神经元数目的单隐藏层FNNE 和基于自回归循环神经网络的RNNE，该RNNE 由于添加额外反馈神经元复杂度有所提高，但是得到了更优的性能。然而，上述提到的NN 结构中隐藏层只有一层或者两层，隐藏层层数和隐藏层神经元数目的对神经网络均衡器的影响仍是未知的。

本课题组对单层隐藏层RNNE 和2 层隐藏层RNNE 在光IM/DD 系统中的性能进行了研究［16］。在此基础上，为了探究隐藏层数目对RNNE 性能的影响，寻求低复杂度高效的均衡方案，本文进一步分析了增加隐藏层数目对均衡器算法复杂度降低的有效性，并制订了隐藏层神经元数目的选择策略。搭建了112 Gbps 20 km 的PAM-4 光IM/DD 传输仿真平台，在不同维度下定量分析了隐藏层数目对RNNE 误码率（Bit Error Rate，BER）及算法复杂度的影响，结果表明2 层隐藏层RNNE 具有更优的性能。另外，通过遍历隐藏层内部神经元的数目、分析其对均衡器性能的影响，统计得出隐藏层神经元数目的优化策略，对多层RNNE 实现非线性均衡具有一定的指导意义。

1 基本原理

1.1 RNNE 神经网络均衡器结构

单隐藏层FNNE 的结构如图1。这是一个两层网络，包括隐藏层和输出层，输入层不计入其中。图1 中x代表均衡器的输入，l是输入的数目，h代表隐藏层神经元，n是隐藏层神经元的数目，y是均衡器的输出，代表均衡后的值。RNNE 结构中D代表四电平判决模块，Z代表延时模块，d是判决后反馈的符号，k是反馈的数量。与FNNE 的结构相比，RNNE 重用输出判决后的符号的作为输入，在预测当前输出时，过去预测的输出作为输入提供了额外的信息。因此，在强非线性系统中，RNNE 具有更优的均衡性能。

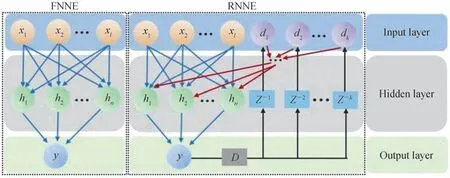
图1 单隐藏层NN 均衡器的结构Fig.1 Schematic of the single hidden layer NN equalizers

1.2 均衡器算法复杂度衡量

在衡量RNNE 的性能时，除了BER 还有一个重要的参数指标是算法复杂度。首先考虑单隐藏层FNNE 的算法复杂度。因为乘法比加法复杂得多，所以均衡一个符号所需要的执行的乘法次数用来表示FNNE 的算法复杂度［11］。为了恢复一个符号，将l个相邻的采样序列作为输入神经元，然后通过n个隐藏层神经元的计算，得到一个输出。在图1 FNNE 中，每个隐藏层神经元都可以看做是一个计算单元，其内部计算可以表示为

式中，yh为当前隐藏层神经元的输出，wi为对应输入xi的权重，b是偏置。w和b需要通过训练来优化。f(·)为激活函数，用来引入非线性。ReLU(x)结构简单，同时也能很好地解决IM/DD 系统中的非线性，作为激活函数，其表达式为

由于ReLU(x)函数只需要做简单判断，其复杂度可以忽略不计。根据式（1）可以计算出一个隐藏层神经元中需要的乘法次数等于输入神经元的数目l，输出神经元需要的乘法次数等于上一层的输入数目n。FNNE 均衡一个符号需要的乘法总数NFNN等于所有神经元中乘法的次数总和，可表示为

类似地，单隐藏层RNNE 的算法复杂度也使用均衡一个符号需要的乘法次数NRNN表示，图1 中RNNE与FNNE 不同的是：输入神经元除了相邻的采样序列xi，还包括判决反馈符号dj，其中一个隐藏层神经元的计算可以表示为

根据式（4），RNNE 每个隐藏层神经元中乘法次数等于输入神经元的数目（l+k），和输入数目为（l+k）的FNNE 相等。RNNE 均衡一个符号需要的乘法总数NRNN同输入数目为（l+k）的FNNE 相等，可表示为

多隐藏层RNNE 结构如图2，第i层隐藏层的神经元数目为ni（i=1，2，...，m），其中第一层隐藏层神经元输出可用式（4）表示，第i层（i=2，...，m）隐藏层神经元输出可表示为

图2 多隐藏层RNNE 的结构Fig.2 Schematic of the multiple hidden layers RNNE

特殊地，当每层神经元的数目都相等时，即n1=n2=...=nm=n，式（7）可简化为

1.3 RNNE 的初始化和训练

对于不同结构的RNNE 在均衡信号之前需要通过训练来优化均衡器的参数，这些参数包括所有的权重和偏差。对于一个m层隐藏层RNNE 一共包括m+1 组权重和偏置，分别位于输入层和隐藏层、隐藏层和隐藏层，隐藏层和输出层之间。在训练之前，需要对这些参数进行随机初始化，然后通过反向传播和Adam 优化器进行小批量梯度下降训练。训练超参数的设置：学习率设置为10-3，最大迭代轮次设定为100，小批量梯度下降的批次大小为16。每批数据正向传播后，计算均方误差LMSE，其表达式为

式中，s为小批量梯度下降的批次大小，为一批数据中第i个原始符号，yi为第i个符号对应的均衡器输出。得到LMSE后进行反向传播，再更新权重和偏置以最小化均方误差。在每轮迭代完成后，使用RNNE 分别均衡训练集和测试集上的数据，得到均衡后的符号，并计算BER。随着迭代轮次的增加，参数不断优化，LMSE值逐步减小，测试集上的BER 也越来越小。当测试集上的BER 不再下降时，网络停止更新，记录下BER 最优时的均衡器参数。

和单隐藏层RNNE 的训练相比，多隐藏层均衡器的误差函数的收敛会变缓甚至无法收敛，使得经过100轮迭代更新后的RNNE 不能在测试集上得到理想的BER。增加迭代轮次可使误差函数收敛来解决这个问题，但训练时长也会相应增加，所以训练时使用迁移学习而不是单纯的增加迭代轮次。在迁移学习的帮助下，可以显著减少迭代轮次和训练符号数目，从而保证大大缩短NN 训练时间。同一个NN 结构在不同场景下的迁移学习的有效性已经被验证［17］。本文将其推广到同一场景下的不同NN 结构，在训练2 层隐藏层RNNE 时，将已经训练好的单隐藏层RNNE 的第一组的权重和偏置（输入层和第一层隐藏层之间）赋值给2层隐藏层RNNE 对应位置的参数。这样2 层隐藏层RNNE 可以在单隐藏层RNNE 的参数上继续优化，均方误差可以更快地收敛，从而大大缩减训练所需要的迭代轮次，缩短训练所需要的时间。类似地，对m层隐藏层RNNE 的训练，可以直接加载对应m-1 层隐藏层RNNE 的前m-1 组的权重和偏置。

1.4 光IMDD 传输仿真平台搭建

为了衡量多隐藏层RNNE 的BER 和复杂度性能，使用VPItransmissionMaker 13.1 搭建的仿真平台如图3。ERIKSSON T A 等［18］指出：基于机器学习的均衡器的性能可能被高估了，因为在使用伪随机二进制比特序列（Pseudo-random Bit Sequence，PRBS）训练模型情况下，NN 可以识别PRBS 数据的模式，从而获得卓越的性能。因此，在发射机处200 000 PAM-4 符号由MATLAB 随机生成的，其中50 000 用于训练，其余用于测试。PAM-4 信号经过4 倍上采样和滚降系数为0.1 的奈奎斯特滤波整形后通过数模转换器（Digital to Analog Converter，DAC）变成模拟信号，再被电吸收调制器（Electro-absorption Modulator，EAM）调制到1 550 nm 波长的激光上。调制好的光信号经过标准单模光纤（Standard Single-mode Fiber，SSMF）传输20 km 到达接收端。在接收端，可变光衰减器（Variable Optical Attenuator，VOA）将接收光功率（Received Optical Power，ROP）调整到合适的水平，光信号被检测响应度为0.65 A/W 的光电检测器（Photo-detector，PD）接收转变为电信号，然后通过采样率为224 GSa/s、分辨率为8 位的模数转换器（Analog to Digital Converter，ADC）变为数字信号，最后进入离线数字信号处理（Digital Signal Processing，DSP）模块。该模块包括匹配滤波、重采样、RNNE 均衡和 BER 计算。仿真采用的参数如表1。

图3 用于112 Gbps PAM-4 光链路的多隐藏层RNNE 的验证设置Fig.3 Verification setup of the multiple hidden layers RNNE for a 112-Gbps optical PAM-4 link

表1 PAM-4 光链路的仿真参数Table 1 Parameters of optical PAM-4 link

2 结果与分析

2.1 隐藏层内神经元数目选择策略

为了得到最优的BER 及复杂度性能，对于多隐藏层RNNE 结构的确定，需要考虑每层隐藏层中神经元数目的选择。图4 中散点代表不同结构的2 层隐藏层RNNE，数字表示RNNE 隐藏层神经元数目，具体地，（u，v）表示第一隐藏层具有u个神经元、第二隐藏层具有v个神经元的RNNE。图4 中固定第一隐藏层神经元的数目，然后遍历优化第二隐藏层神经元的数目得到了不同结构RNNE 的BER 及复杂度性能。结果表明，均衡器的BER 及复杂度性能最优时，第二隐藏层的神经元数目与第一层相近。然后将最优的均衡器结构用实线拟合，同时将第二和第一隐藏层神经元数目相等的均衡器作为目标结构用点划线拟合。对比两条曲线，发现选择神经元数目相等的均衡器结构可以得到与最优结构相近的性能，同时避免了大量重复的遍历训练。

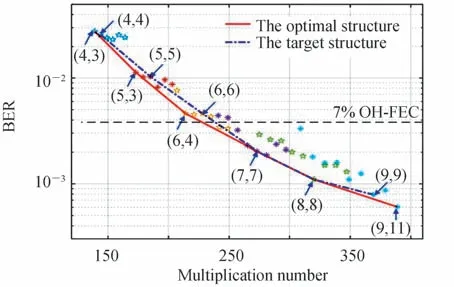
图4 2 层隐藏层RNNE BER 和乘法次数的关系Fig.4 BER vs.multiplication numbers for two hidden layers RNNE

2.2 多层隐藏层网络复杂度和性能对比

图5 显示了隐藏层数目不同的RNNE 算法复杂度和BER 之间的关系。从整体的趋势来看，随着隐藏层神经元数目的增加，RNNE 的均衡一个符号的所需乘法次数相应增加，BER 结果也越好。对比单层和2 层隐藏层RNNE 的曲线，发现在同一BER 阈值下，2 层隐藏层RNNE 的复杂度小于单隐藏层RNNE 的复杂度，具体复杂度对比如表2。

表2 不同阈值下多隐藏层RNNE 的算法复杂度Table 2 NRNN of multiple hidden layers RNNE at different thresholds

图5 多隐藏层RNNE BER 和乘法次数的关系Fig.5 BER vs.multiplication numbers for multiple hidden layers RNNE

在BER 为10-2、3.8×10-3（7% OH-FEC）和10-3三个阈值下，2 层隐藏层RNNE 相比于单隐藏层RNNE的算法复杂度理论上分别可以降低8.3%、15.6%和23.3%。随着复杂度的增加，降低复杂度的效果也越好。但是在同一BER 阈值下，隐藏层数目继续增加，RNNE 的算法复杂度反而会增加。为了进一步研究隐藏层数目对RNNE 性能的影响，在隐藏层神经元数目相同的条件下，对比多隐藏层RNNE 的BER 性能，具体如表3。

表3 隐藏层神经元数目相同的多隐藏层RNNE 的BER 性能Table 3 BER of multiple hidden layers RNNE with the same hidden neurons number

观察表3 中数据，增加RNNE 的隐藏层层数和隐藏层神经元的数目均可以提高均衡器的BER 性能。对比隐藏层神经元数目相同的RNNE，发现增加隐藏层数目总是可以降低BER，虽然增加隐藏层数目带来的算法复杂度增加是一样的，但是增加第三层隐藏层带来的BER 优化远远小于增加第二层隐藏层带来的BER 优化。隐藏层神经元数目相同的多隐藏层RNNE 的算法复杂度对比具体如图6。

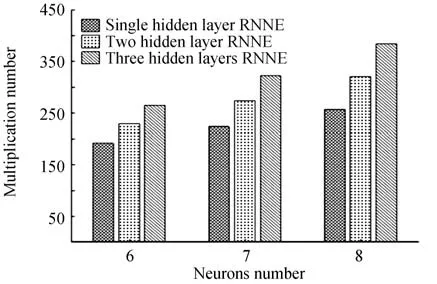
图6 隐藏层神经元数目相同的多隐藏层RNNE 的算法复杂度对比Fig.6 Comparison of multiplication numbers of multiple hidden layers RNNE with the same hidden neurons number

2.3 不同ROP 下网络结构的性能

通过调节VOA，绘制了不同接收光功率下三种RNNE 的BER 性能，如图7。具有10 个隐藏神经元的单隐藏层RNNE 的复杂度为 320，具有12 个隐藏神经元的单隐藏层 RNNE 的复杂度为 384，分别如图7 中RNNE（A）和（B）。对于图7 中2 层隐藏层的RNNE，每层神经元数目为8，对应的乘法数是320。图7 中2 层隐藏层RNNE 和单隐藏层RNNE（A）相比，复杂度降低了16.7 %，同时得到了相似的性能。另外，在相同的复杂度下，2 层隐藏层RNNE 比单隐藏层RNNE（B）具有更好的BER 性能，在7 % OH-FEC 阈值下，系统整体功率预算提高约1 dB。图8 展示了-8 dBm 接收光功率下的单隐藏层RNNE（B）和2 层隐藏层的RNNE的眼图。

图7 不同结构的RNNE 的BER 和ROP 的关系Fig.7 BER vs.received optical power for single and two hidden layers RNNEs

图8 ROP为-8dBm的眼图Fig.8 Eye diagrams at -8 dBm ROP

3 结论

本文研究了IM/DD 系统中多隐藏层RNNE 隐藏层层数及隐藏层神经元数目对神经网络均衡器性能的影响。针对2 层隐藏层RNNE，固定第一隐藏层神经元的数目，比较第二隐藏层神经元数目不同的RNNE的性能，结果表明：对于2 层隐藏层的RNNE，隐藏层神经元数目相近时，其BER 及复杂度性能最优。对于多隐藏层的RNNE，通过定量研究隐藏层数目对RNNE 的BER 及算法复杂度的影响，发现最佳隐藏层数目为2。在相同BER 性能条件下，2 层隐藏层RNNE 相较于单隐藏层RNNE 最多可以实现 23.3% 的复杂度降低。在同一算法复杂度条件下，2 层隐藏层RNNE 比单隐藏层RNNE 在7 % OH-FEC 阈值下功率预算提高1 dB 左右。本文以均衡器的最优结构为目标，分别量化研究了隐藏层层数和隐藏层神经元数目对RNNE 性能的影响，为神经网络解决IM/DD 系统的非线性时隐藏层层数和隐藏层神经元数目的选择提供了参考。