考虑快递配送路线中断不确定的集散中心选址研究
孙仕豪 (国家邮政局发展研究中心,北京 100868)
0 引 言
在快递网络中,物理层为最基础、最重要的组成部分;它由总公司、集散中心、基层配送网点及各级运输路线共同组成。集散中心作为快递网络的重要组成部分,对整个快递业务的稳定运行起决定性作用。在实际的快递网络中,结合快递货源分布零散且单笔数量小的特点,集散中心可作为整个快递网络的枢纽中心,产生规模经济效益。杨从平等提出对快递网络节点的流量和配送时间进行约束,构建出一种基于全连接网络与树形网络的最优网络拓扑。在研究优化快递网络时,将配送时间与快递量两个不确定量进行约束后,确定对应条件下的网络结构和集散中心,为一些特殊要求的快递业务设计提供理论依据[1]。朱兴林在传统模型分析的基础上综合考虑物资需求和运输时间的不确定性,构建成本与时间最小的双目标公路应急资源点选址的确定模型与鲁棒优化模型,从而保障突发交通条件下公路应急系统的正常工作状态[2]。在进一步优化网络中心选址的过程中,刘晓慧对比常用的配送中心选址方法,例如层次分析法、重心法和Baumol-Wolfe(鲍姆尔-沃尔夫)法等,根据运筹学理论,对各种选址方法进行了比较和分析,确定了适合物流配送中心选址的方法,采用过滤法求解整数规划数学模型,确定了物流配送中心的最佳地址,为快递中心更为科学的选址提供了有效参考[3]。
综上所述,关于确定条件下的快递网络结构、快递配送路线及选址都有深入研究。然而,关于快递网络在不确定条件下的研究,例如时间需求变化等方面却很少被涉及。本文以快递网络为基础,结合不确定理论对不确定时间需求的选址问题进行研究。
1 考虑配送路线强度的集散中心选址
1.1 问题描述
在实际选址问题中,各顶点间的权值一般为各顶点间确定的距离权值,通过距离权值从所有顶点中选择一个离其他顶点距离最小的顶点作为选址目标。在单一目标的选址方法中,重心法、交叉中值法及连通图中心法被较为广泛地应用。而前两种选址方法是在现有服务网点的基础上,寻找一个新的地点作为分拨中心(也被称为连续型选址)。这类选址方法得到的位置可能存在以下问题:选址地点因自然因素不能建造分拨中心;选址位置与企业的发展策略不符。利用连通图中心法,在已有的服务网点中选择一个到其他服务网点配送时间总和最小的作为集散中心(离散型选址),可以避免上述原因引起的选址问题。但该算法应用于集散中心选址时也有不足之处。由于集散中心选址时要考虑把快递配送时间作为权值,而配送路线常常出现不确定性中断,导致配送路线上的配送时间不能确定,快递服务可能出现配送延迟或整体配送时间过长,导致集散中心选址失效,因此快递企业在进行集散中心选址时需要考虑不确定中断的影响。
1.2 相关定义
不确定测度、不确定变量、不确定分布组成了不确定理论的3个最基础概念。通过对3种不确定理论的概念进行理论推导,将不确定测度、不确定变量、不确定分布转化,并将不确定理论应用于实际问题中。
1.2.1 不确定测度
定义1:设Γ是一个非空集合,ℒ是Γ上的σ-代数。ℒ中的每个元素Λ称为事件。如果一个从ℒ到实数集R的集函数M满足以下条件。
公理1:对于全集Γ,有M{Γ}=1(规范性);
公理2:对于任意的事件Λ,有M{Λ}+M{Λc}= 1(对偶性);
公理3:对于有限的事件序列 {Λi}+∞i=1,有

则称M为不确定测度,三元组(Γ,ℒ,M)为不确定空间(次可加性)。
不确定测度的性质如下。
定理1(Liu):对于任意事件Λ,如果M是Λ的一个不确定测度,则有0≤M{Λ}≤1[4];
定理2(Liu):不确定测度M具有单调性。任意两个事件Λ1和Λ2,若Λ1CΛ2,则M{Λ1}≤M{Λ2}。
在以上不确定测度理论的基础上,Gao对连续的不确定测度进行探究,You和Zhang分别给出了关于不确定测度收敛的一些定理。这些都是不确定测度研究领域的主要工作。
1.2.2 不确定变量
定义2(Liu):从不确定空间(Γ,ℒ,M)到实数集R的可测函数ξ称为不确定变量。即对于任意Borel实数集B,集合{ξ∈B}={γ∈Γ|ξ(γ)∈B}是ℒ中的一个事件[4]。
定义3(Liu) :设n个不确定变量ξ1,ξ2,…ξn,如果任意n个Borel集B1,B2,…,Bn(在R中存在)都有

则认为n个不确定变量相互独立[4]。
1.2.3 不确定分布
不确定分布是不确定变量的一种研究手段,目的是更简便直观地研究不确定变量。
定义4(Liu):对于不确定变量ξ,定义不确定变量ξ的不确定分布为Φ,Φ(x)=M{ξ≤x},Ax∈R[4];
定义5(Liu):如果不确定变量ξ的不确定分布的反函数Φ-1(α)在α∈(0,1)区间存在且唯一,那么称ξ是正则的。此时,称Φ-1为ξ的逆不确定分布[4]。
a.若不确定变量ξ有如下线性不确定分布函数:

则称ξ为线性不确定变量,记为ℒ(a,b),其中a,b为实数且a<b。由不确定分布定义可得其逆不确定分布为:

b.若不确定变量ξ有如下“之”字形不确定分布函数:
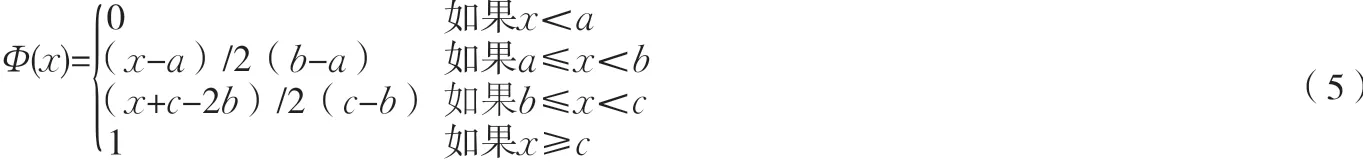
则称ξ为“之”字形不确定变量,记为Z(a,b,c),其中a,b,c为实数,且a<b<c。由不确定分布定义可得其逆不确定分布为:
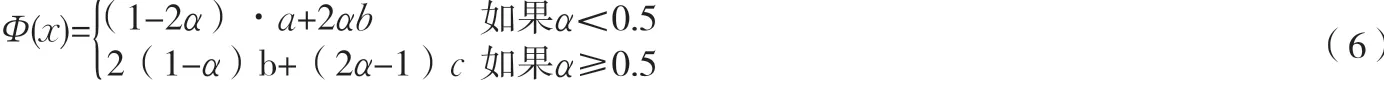
定理3(Liu):如果Φ1,Φ2,…Φn是n个相互独立的正则不确定变量的ξ1,ξ2,…,ξn不确定分布,则ξ=f(ξ1,ξ2,…,ξn)为一个正则不确定变量。若以x1,x2,…,xn为条件,f(x1,x2,…,xn)是严格单调递增的,则ξ的逆不确定分布为Ψ-1(α)=f(Φ-11(α),Φ-12(α),…,Φ-1n(α)),α∈(0,1);若以x1,x2,…,xn为条件,f(x1,x2,…,xn)是严格单调递减的,则ξ的逆不确定分布为[4]:
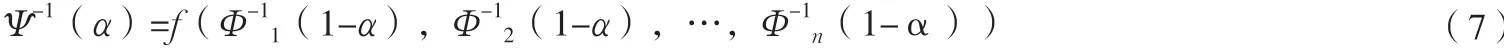
1.3 模型建立
在模型建立之前,需要对研究对象以及研究条件进行假设:
a.在已知的服务网点中选择分拨中心,不考虑新建其他网点;
b.各配送路线的配送时间是相互独立的,有限的;
c.分拨中心与服务网点间的配送路线为无向的;
d.配送路线都是满足配送时间要求的,若配送时间超出要求,则不选取该配送路线。
符号说明:
设快递网络为N=(Vi,Lz,dij),
i为可能被选为分拨中心的集合,i=1,2,…,n;
j为服务网点的集合,j=1,2,…,n;
Lz为配送路线集合,z=1,2,…,m;
dij为配送时间;
D(dij)为所有配送时间;
fdv0为分拨中心选址函数,v0为集散中心选址。

1.4 不确定模型向确定模型转化
模型中配送路线的配送时间为不确定变量。因为不确定配送路线是否堵塞,所以不能直接对集散中心进行求解。需要通过不确定理论进行转化后再求解。
对照不确定网络理论,由不确定测度的定义1可知不确定测度应有规范性、对偶性、次可加性。配送路线影响配送时间的不确定堵塞满足条件,本文设不确定堵塞g为不确定测度。
由不确定变量的定义2、3可知,具有不确定性的、有限的、相互独立的数值可作为不确定变量,因此本文设配送时间为不确定变量dij。
由不确定分布的定义4可知,配送时间与不确定堵塞组成了不确定分布g=Φ(dij)=M{d≤D},Ad∈R。
因为配送时间为真实存在且有范围的数值(aij<dij<bij),配送时间又随着不确定堵塞情况而变化,所以设配送时间为线性不确定变量,有如下不确定分布:
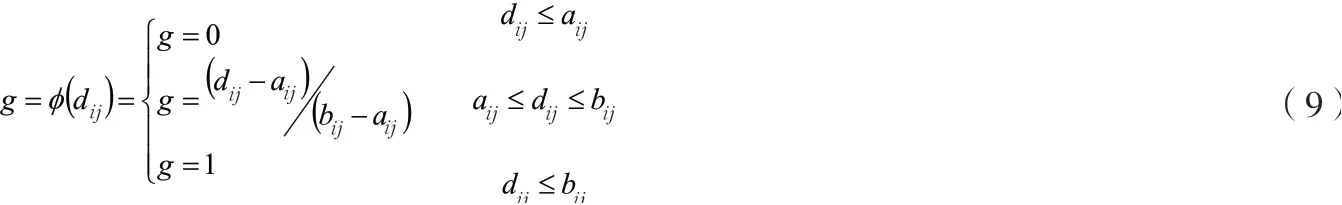
该不确定分布的反函数为:

由定义5可知,dij为正则不确定变量且dij的逆不确定分布为Φ-1(g)。
因此,利用不确定分布计算得到各配送路线的配送时间,形成配送时间表;再通过Prim最小生成树算法选择符合配送时间标准的配送路线,得到最短总配送时间的最小生成树,在此基础上利用连通图中心算法fd选择分拨中心。
综上所述,由于dij为不确定变量,因此定义快递网络N=(V,L,d)为不确定网络。文献[10]可证明fd为单调函数,dij有正则不确定分布Φz(g),z=1,2,…,m。所以,可设快分拨中心的不确定分布为Ψ(g),即Ψ(g)=Μ{fd(Φ(g))<R}。
由定理3可知,Ψ(g)=fd(Φz(g))的不确定分布也存在逆分布为Ψ-1(g)=fd(Φ-11(g),…,Φ-1m(g)),g∈(0,1)。
转化后的模型如下:
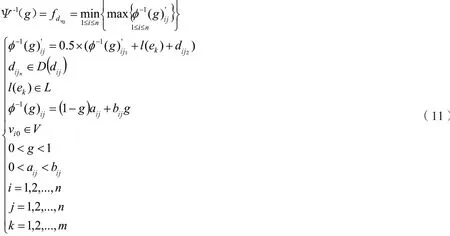
通过转化的模型可以把不确定的配送时间转化为确定的配送时间,同时根据不同时间标准对配送路线进行选择,再通过连通图中心算法选择该状况下集散中心的位置。
2 算例分析
图1为不确定配送时间快递网络N=(V,L,dij),V表示快递网络中的网点,L表示网点间的配送路线,dij表示任意两个服务网点间的配送时间,g表示配送路线的不确定堵塞,(aij<dij<bij,aij为最短配送时间,bij为最长配送时间)。各配送网点间的配送时间范围见表1。
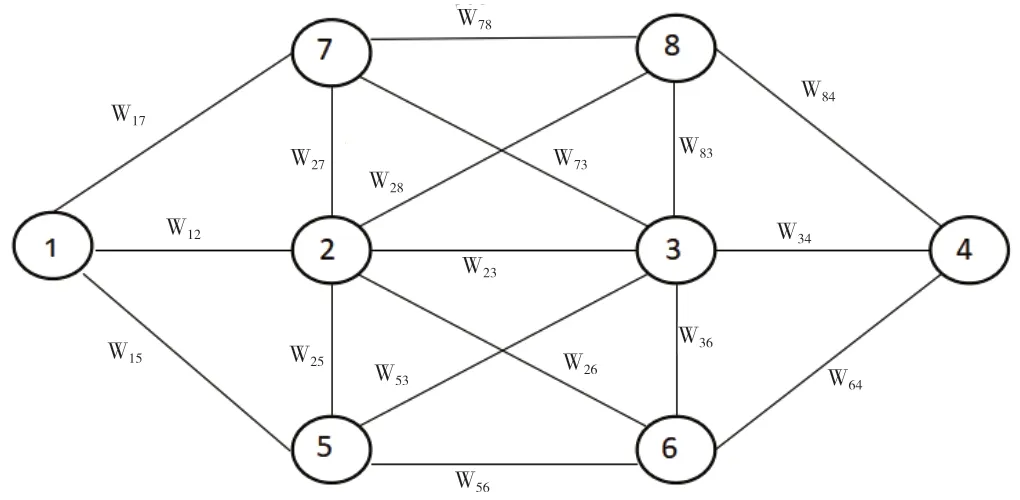
图1 不确定配送时间快递网络N
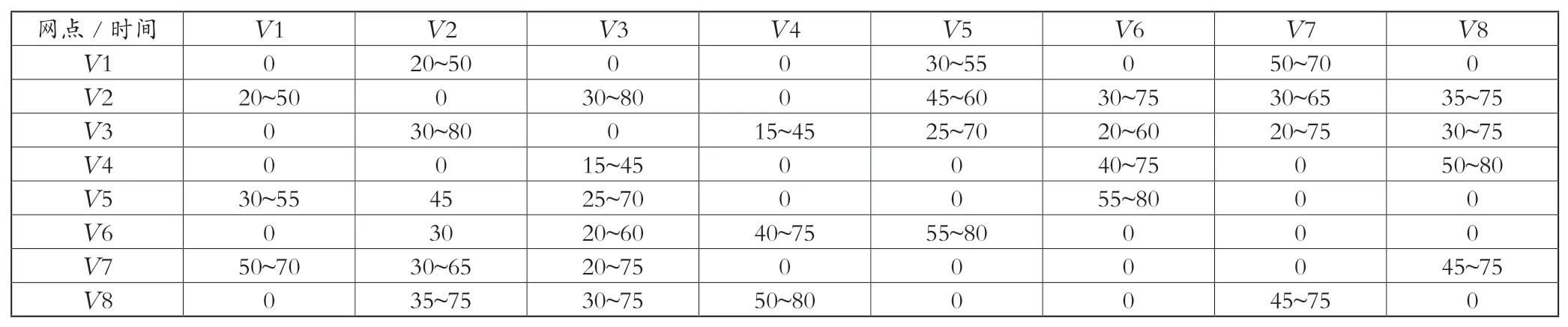
表1 不确定配送时间 小时
在上述条件下,快递企业希望在这8个网点中选择1个集散中心,该集散中心满足到其他7个网点的配送时间综合最小,同时选择的配送路线能符合有关规定。
由国家邮政局发布的《快递服务》中第四章第四条提出的服务时效里明确提出快递服务时限指快递服务组织从收寄开始,到第一次投递的时间间隔。除了与顾客有特殊约定(如偏远地区)外,服务时限有以下要求:
a.同城快递时限不超过24h;
b.跨城市快递时限不超过72h。
若配送时间小于24h,配送时间按原值计算;若配送时间大于72h,不能选取该配送路线,配送时间表示为∞;配送时间在24h到72h之间,则表示存在不确定堵塞,通过模型转化为对应的不确定配送时间,所以当不确定堵塞g=0.5时,配送路线的配送时间见表2。
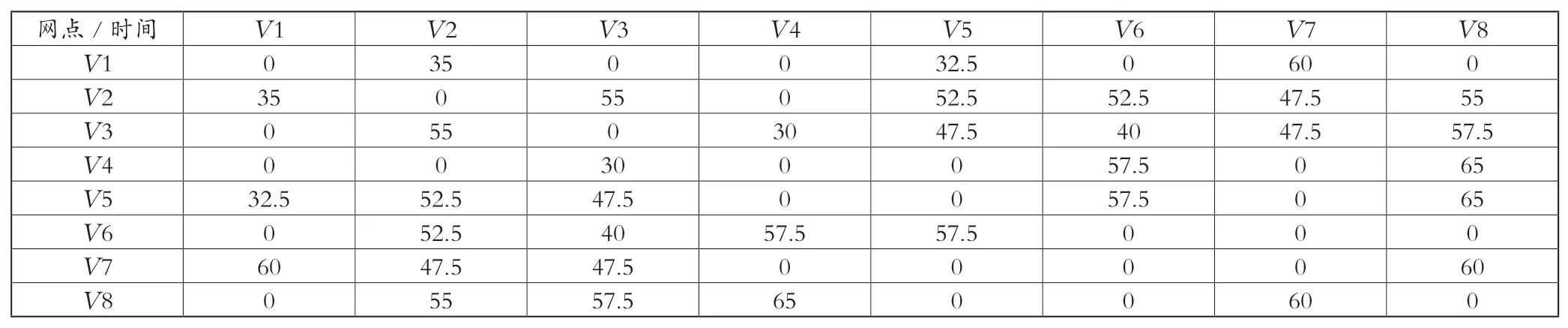
表2 不确定堵塞g=0.5时的配送时间 小时
当不确定堵塞g=0.7时,配送路线的配送时间见表3。

表3 不确定堵塞g=0.7时的配送时间 小时
此时可以通过Prim算法选取符合配送条件的配送路线作为最小生成树,具体过程如下:
当g=0.5时,配送网络的最小生成树在快递网络中选取的配送路线L为l12、l15、l27、l53、l34、l36、l38。此时配送路线的配送时间为d12=35h、d15=42.5h、d27=47.5h、d53=47.5h、d34=30h、d36=40h、d38=52.5h。
当g=0.7时,配送网络的最小生成树在快递网络中选取的配送路线L为l12、l15、l27、l53、l34、l36、l38。此时配送路线的配送时间为d12=41h、d15=47.5h、d27=54.5h、d53=56.5h、d34=36h、d36=48h、d38=61.5h。
由此可以得到,任意不确定中断下的各配送路线的配送时间,代入连通图中心的程序中,选择到离其最远的服务网点配送时间最少的集散中心dv0。当g=0.5时代入模型后,得到集散中心为2号;当g=0.7时代入模型后得到集散中心为3号;同理输入g=0.1~0.9,通过fd得到对应的分拨中心,过程不一一列举。具体数据见表4。

表4 不确定堵塞与集散中心位置
由表可知,g=0.1、0.2、0.3、0.4、0.5、0.6时,集散中心为2号;g=0.7、0.8、0.9时,集散中心为3号。此时可得,若配送路线的不确定堵塞g<0.7时选择2号作为分拨中心,不确定堵塞g>0.7时则选用3号为分拨中心。
3 结 语
快递企业在选择快递网络时需要考虑快递配送快速、少量的特性,快递集散中心在快递网络中起核心作用,在配送、中转、库存等方面有决定成本高低、服务质量优劣的作用。关于集散中心的选址问题,一般方法都基于确定的路线后,选择一个到其他所有网点距离最短的网点作为集散中心;或者考虑其他因素权重的大小,以权重的形式计算,选择期望的极值作为集散中心。
而在实际的快递配送与快递网络中,配送路线与影响配送时间的因素是不能确定的,这也决定了快递集散中心的选择不能唯一确定。本文基于不确定理论,以配送时间为不确定量,配送强度为选择条件,通过Prim算法与连通图中心算法,推出对应不确定时间的集散中心。此方法有3个优点,一是集散中心的选址方法,在现有网点的基础上选择分拨中心,能有效地利用现有资源;二是考虑了快递网络的配送路线是否符合要求,应用Prim算法求得符合要求的最小生成树,为企业选择了网点全连通且总配送时间最短的路径;三是引入了不确定因素,集散中心选址由不确定堵塞与配送时间决定,更符合如道路堵塞、交通管制、疫情隔离等突发条件下的实际选址情况。最后给出算例得到了考虑配送路线强度的集散中心。

