静力弹塑性方法在双圆柱墩桥梁抗震设计中的应用

郑佐雄

（云南工程勘察设计院集团有限公司，云南 昆明 650051）

0 引言

桥梁负荷随着车流量的增加、车辆重载化而加重，保证桥梁的稳定性是设计阶段不容忽视的目标。抗震性能对桥梁受力特性有明显的影响，因此抗震是桥梁设计中的重点内容，科学的抗震设计方法有利于保证抗震方案的可行性，维持桥梁结构的稳定性。静力弹塑性方法因具有操作便捷、实用性强等特点而在桥梁抗震设计中得以广泛应用，本文围绕具体的应用要点进行探讨，加深对静力弹塑性方法的认识，优化应用效果。

1 Pushover 方法

1.1 应用原理

对桥梁结构做抗侧力计算，据此评估抗震性能。在分析过程中，向结构施加某侧向力，并随着分析的进行而逐步单调增加，使结构受到力的作用。结构在持续受力后发生阶段性的变化，从弹性阶段到开裂、屈服直至破坏，施加力的过程中需采集结构的相关数据，并进行汇总，生成结构能力谱曲线，建立坐标系，共同绘制结构能力谱曲线和地震反应谱曲线，以图形直观化的方式评估在特定地震作用下结构的具体表现。

根据影响机制，抗震评估结果的准确性主要取决于加载模式和目标位移两个方面，是提高评估结果准确性时应重点关注的对象，例如，需合理选择加载模式，设定科学的目标位移。静力弹塑性分析兼具多项优势，例如，校核结构在多遇地震的弹性设计，确定结构在罕遇地震时的破坏特性，从中锁定最薄弱部位，采取有针对性的修复措施，保证结构稳定，使预先设定的功能得以有效发挥。

1.2 Pushover 方法的假设

随着理论研究的深入和经验的积累，Pushover分析在双圆柱桥墩抗震设计及其工程设计中得到广泛应用，但在设计中有诸多注意事项。为妥善应用Pushover 方法进行桥墩抗震设计，需做出以下两种假设。

（1）结构在地震作用时的反应特性由第一振型所决定。

（2）用桥梁结构地震作用不变形状向量表示桥梁在高度方向的变形状况。

在建立前述假设的基础上应用Pushover 方法，可将桥梁的多自由度结构转变为单自由度结构，以便抗震设计工作的高效开展。其中，第一阶振具有重要的分析价值，原因在于其能够作为桥梁结构在地震作用时具体反应的表现途径，以Pushover 方法组织结构抗震设计是一项具有可行性的设计工作模式[1]。

2 双柱框架桥墩设计及荷载计算

2.1 桥墩尺寸设计及配筋方式

以现浇桥墩构件的抗震性能为重点研究对象，根据桥梁实际尺寸，按照1:4 的比例缩尺生成待分析构件的尺寸，关键结构包含承台（1 个）、普通钢筋混凝土桥墩（2 个，等高）、盖梁（1 个），施工所用混凝土的强度等级分别为C30、C40、C50，桥墩主筋由8 根HRB400 级普通钢筋组成，箍筋直径取80 mm，以120 mm 的间距依次布设到位，遇节点部位时以高密度的方式布置，借助足量的钢筋维持节点部位的稳定性。

有限元模型的建立采用Midas Civil 软件，按C40 混凝土强度等级进行桥墩的建模，承台采用一般支承，限制自由度，桥墩与盖梁、承台的边界均为刚性连接[2]。

2.2 静力荷载计算

墩顶容许位移以推倒分析的方法计算而得，首先求得容许转角，而此项数据需根据横桥向弯矩而定，因此计算的关键在于依次确定横桥向弯矩、容许转角。具体计算思路如下。

（1）墩柱轴力为恒载轴力，建模时两点加载，结果显示上部荷载为670.1 kN，若平均分配，则单个桥墩墩顶施加335 kN 的力。

（2）在建立材料的本构模型时，强度取强度标准值，墩柱塑性铰区截面超强弯矩以弯矩曲率曲线计算而得。塑性铰截面如图1 所示，其中阴影部分为约束混凝土，剩余部分为非约束混凝土。

图1 塑性铰截面

（3）钢筋的滞后模型采用双折线模型，骨架中钢筋弹性模量 E1=200 000 N/mm2，E1/E2=0.001（E2为约束混凝土弹性模量），抗拉强度fy=400 N/mm2。对于约束混凝土，截面和约束钢筋均为矩形，而混凝土构件将原强度乘以0.85 的折减系数。桥墩截面的弯矩曲率曲线如图2 所示。

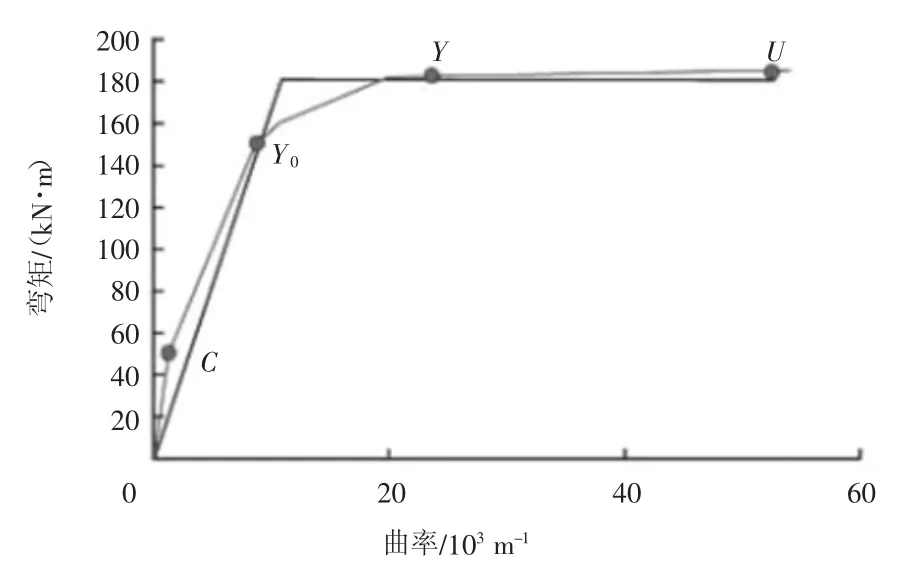
图2 桥墩截面的弯矩曲率曲线

结合图2 展开分析：C 点属于关键的转折点，即混凝土开始开裂的点，在此之前为弹性阶段；Y0为钢筋开始发生屈服的点，C 点至Y0点为弹塑性阶段；Y为构件进入完全屈服的点，Y0至Y 点对应的是构件的屈服阶段；U 点为结构达到极限破坏的点，Y 点至U 点指的是构件进入塑性阶段。在图形阶段性分析的基础上，确定弯矩曲率数据，如表1 所示。

表1 弯矩曲率数据

（4）根据延性桥墩顺桥向和横桥向的剪力进行计算，确定左墩、右墩相应于其超强弯矩的剪力值分别为197.9 kN、300.5 kN，据此进一步计算，确定各墩柱的剪力值之和，结果为498.4 kN，将其施加至盖梁质心处，计算确定左墩柱、右墩柱的轴力分别为52.5 kN、640.1 kN，可见各墩柱的轴力存在明显的差异[3]。

（5）对剪力产生的轴力和恒载轴力进行组合，考虑最不利组合工况，利用Midas Civil 软件计算后确定具体的轴力值，按照前述提及的流程做多次的迭代计算，结果显示相邻两次的剪力和相差3.1%，相较于“各墩柱剪力和相差在10%以内”的要求，3.1%明显更低，因此剪力和的相差量得到有效控制，达到要求。桥墩迭代过程如表2 所示。

表2 桥墩迭代过程

建立有限元模型后，展开分析。为确保分析结果具有参考价值，需要考虑上部荷载产生的轴力、水平计算推力的重力二重效应及桥墩的自重，即对应的是最不利工况。结果显示，左墩、右墩的墩底轴力分别为52.5 kN、640.1 kN，如图3 所示。

图3 墩底轴力

3 Pushover 分析

将上部荷载和结构自重加载至静力荷载计算，后续控制荷载工况，采用位移控制的方法，计算步数取400 步，主控节点为盖梁的中心点。在单元受重力和横向荷载时，出现附加变形和附加内力，因此此处需要考虑重力二阶效应，此时的待分析单元将由于重力作用而加大弯曲变形的幅度。

铰特性：骨架为三折线类型，单元类型为柱单元，初始刚度、第二刚度、第三刚度根据弯矩曲率曲线计算而得。在明确刚度值后，求取左墩的刚度折减系数，即 α1′=0.059 962、α2′=0.001 806，按照相同的思路进行分析，确定右墩的刚度折减系数，有α1=0.152 453、α2=0.064 049。在求取各项数值的基础上，结合弯矩曲率曲线，实现对三折线的自定义。随后，将铰特性分配给墩单元，极限容许曲率为0.02 526。以分步的方式进行操作，最终使铰单元达到极限曲率[4]。以 29 单元、38 单元、39 单元、48 单元为例，各自达到极限曲率的加载步如表3 所示。

表3 铰单元达到极限曲率的加载步

水平力的作用部位集中在盖梁的中心区域，以特定的加载步进行操作后，产生具体的试验现象。试验控制水平方向的位移，计算钢筋混凝土本构模型，明确混凝土开裂、初始屈服、屈服、极限4 种状态各自对应的数据，综合多项数据对桥墩的特性进行系统性的分析。在明确此类数据的基础上，综合考虑Pushover 的计算结果，确定各铰单元的极限容许加载步，经过对每步的分析可以得知，桥墩在第31 步被推覆，此时桥墩各单元的水平方向位移可通过查看Midas Civil 位移等值线的方法确定。在达到规定的极限转角时，现浇桥墩的位移为7.8 cm，将此部分数据结合表3 的内容，确定最小的极限破坏位移。除此之外，进一步考虑作用在盖梁上的水平力，此项数据的确定可以通过查看Midas Civil 的计算结果而实现，作用在盖梁中心部位的水平力在极限容许转角的条件下达到351.7 kN，具体如图4 所示。

图4 桥墩横桥向水平力

通过对计算模型的分析，可确定在极限容许位移时构件所受的弯矩。其中，对弯矩值造成影响的关键因素是作用在盖梁上的水平力，其是弯矩控制中的重点考虑对象。经对比分析可以发现，其与本构关系模型确定的数值有所区别，即便此部分数据无法与本构关系模型的数据保持吻合，但可用于验证通过弯矩曲率曲线求取的数值，因此仍是一项不容忽视的分析结果[5]。根据图4 可知，首先达到极限破坏状态的是右桥墩下部铰，由于极限破坏状态的出现，桥梁桥墩的受力出现异常，桥墩不具备承载性能。

4 结语

桥梁工程的设计具有系统性，抗震设计作为重要的部分，其设计水平直接对桥梁的使用性能带来影响。通过对桥梁工程实例的分析，本文提出了双圆柱桥梁抗震设计的方法，即静力弹塑性方法，此分析方法操作便捷、实用性突出，统筹兼顾多项关键性的影响因素，进而做出全面的考虑和周全的设计，有效提高桥梁的抗震设计质量。基于抗震设计方案开展桥梁建设工作，建成的桥梁结构稳定可靠，满足安全出行和桥梁耐久稳定的要求。