基于模型融合方法的IPMSM 转矩预测

杜帅祥 ,韦寿祺 ,梁嘉宁 ,孙天夫 ,王 旭

(1.桂林电子科技大学 机电工程学院,广西 桂林 541004;2.中国科学院 深圳先进技术研究院,广东 深圳 518055)

IPMSM 以其高功率密度、高效率、负载能力强、噪声低等优点,在机器人、工业控制、汽车驱动控制等领域得到广泛应用。在诸如机器狗关节的力矩控制、机器手的抓取力矩控制等方面,在这些对转矩要求高,且限制尺寸等条件的高性能应用场合,不可能通过内置转矩传感器进行控制。因此,研究无转矩传感器转矩参数预测具有重要的意义[1-3]。

永磁同步电机由逆变器电路驱动控制,在运行过程中会受磁体饱和、温升导致的内部参数变化、谐波扰动等影响。通过传统线性数学模型获得的电磁转矩精度低,且含有谐波变量,稳定性差[4-7]。在工业应用中,大多都采用查表法获得转矩数据。查表法是根据离线实验或有限元分析模拟得到的,该方法既简单又具有鲁棒性,但实现该方法非常耗时,需要大量的资源,且每台机器都进行测试不切实际。因此,国内外很多学者对永磁同步电机转矩的精确估算开展研究。

文献[8]采用扩展卡尔曼滤波算法获得电机转速,从而提高电机的估算精度,实现最优电压矢量输出,且减小了转矩、磁链波纹。文献[9]通过扩展卡尔曼滤波算法并根据系统动态和统计模型参数估计转子磁通和负载转矩。但这种方法需要确定正确的模型参数矩阵,否则会出现局部最优解,且该算法需大量的计算,算法复杂,不利于实际应用。文献[10-11]用滑模构建了电机负载转矩观测器,但模型颤振现象受滑模参数影响,不易确定。随着深度学习技术的发展和应用,很多学者将深度学习神经网络应用到非线性系统建模中[12-13]。文献[14-15]用神经网络对电机参数估算,如传统BP神经网络、GA-BP多神经网络。应用神经网络估算转矩是目前最为简单,且效果较好的方法。由于电机运行中的参数波动性和谐波干扰,导致传统神经网络所建立的估算模型精确度略低。神经网络估算模型的性能受内部参数和结构影响大,易陷入局部最优解。目前微处理器实时计算力有限,针对电机转矩环实时控制,不能采用复杂网络算法。

针对以上问题,提出了融合电机转矩线性数学模型和神经网络的模型融合方法,构建了一种结构更简单、估算精度更高的转矩估算模型。模型融合方法显著降低了传统神经网络的结构复杂度,且转矩估算模型具有较高精度,实现了在电机控制系统中的无转矩传感器转矩在线估算。通过模型训练及实验平台验证,所建立的转矩估算模型具有较好的估算精度和稳定性。

1 IPMSM 数学模型与分析

IPMSM 是一个耦合性强的复杂非线性系统,因此要从电机数学模型进行分析。一般地,要将IPMSM 数学模型从abc三相静止坐标系通过Clark和Park变换到d-q同步旋转坐标系进行分析,其等效数学模型如图1所示。

图1 同步旋转坐标系下的IPMSM 的等效模型

d-q轴坐标系下,IPMSM 的d-q轴电压和电磁转矩的数学模型如下:

其中:Ud、Uq、Ld、Lq、Id、Iq分别为电机d-q轴的电压、电感、电流;R为电机定子线圈电阻;ωe为电机转速;ψ为电机永磁体磁链;p为极对数;Te为电磁转矩[16]。

从式(3)可知,电机电磁转矩可由电机d-q轴电感、电流与磁链推导出。因此,电机运行时,受永磁体磁体饱和、谐波干扰和温度影响,电感和磁链等参数发生变化。由数学模型计算的电机转矩与实际转矩相差大,很难对非线性谐波干扰进行建模。

随着人工智能技术的发展,以神经网络为工具应用于现代控制技术,将建模过程直接化、简单化来解决复杂非线性问题逐步成为热门研究方向[17-18]。但由于神经网络本身具有不可避免的缺陷,如易陷于局部最优,网络模型性能依赖于网络参数的设计和大规模神经元计算,等等。为了提高预测效果,研究人员提出了很多优化方法,如GRU、CNN 等复杂网络。但是这种网络对复杂模型建模依赖大规模的网络结构,这为普通控制系统的计算能力带来挑战,也就意味着模型不具有实际应用价值。

从建模对象的角度分析,当利用神经网络方法对转矩整体建模时,神经网络把线性量和非线性量同时包含在网络模型中,这也导致了当神经网络对非线性量估算时,也对线性量进行估算。从神经网络原理可知,神经网络训练是逐步逼近函数的过程,但实际上很难完全拟合。因此,用神经网络对整体建模会引入不必要的误差。

因此,要对IPMSM 转矩进行建模,仅通过数学模型或神经网络方法难以实现精确建模,转矩估算不准确会影响电机无转矩传感器的转矩控制性能。

2 基于模型融合的转矩估算模型

2.1 模型融合方法

该模型以神经网络为框架,嵌入转矩数学模型,将电机转矩模型分为转矩数学模型和神经网络模型。为了改变转矩数学模型在模型中的作用程度对模型性能的影响,引入了数学模型的权值和修正偏置参数。因此,神经网络模型建模过程从转矩模型整体建模到对含有非线性干扰建模,减少神经网络对数学模型建模引起的误差,同时可以降低模型复杂度,避免使用过多神经元来适应模型变化。

以xn表示转矩控制的输入向量,Te(xn)表示式(3)中数学模型计算转矩与输出向量的映射关系,f(xn)表示电机运行中的信号非线性变化,λ表示线性量的权值,ν表示融合模型的偏置,则可将融合模型的转矩估算输出Te*的数学模型表示为

课外是课内的延续和升华，英语教学应主要放在课内，但要学好英语光靠每周几次的英语课是不够的。所以，教师还要大力开展课外教学活动。在开展活动时，教师应根据不同年级、不同层次、不同水平、不同爱好的学生来进行科学组织。比如开展英语游戏、演唱会、朗诵会、演讲比赛、听力比赛等，既可在一个班进行，也可同年级进行，其目的是活跃学生的课外生活，巩固课内所学知识，创造英语学习气氛，培养学生学习英语的兴趣，使课内外结合，相得益彰。

根据电机矢量控制算法(FOC)原理,对IPMSM的控制通常是在d-q坐标系下实现。由式(3)可知,在不考虑运行中谐波影响及电感参数变化等因素,电机输出电磁转矩可由变量d-q轴电流Id、Iq确定。而电机磁链与运行中的电角度θe有关。因此,将变量Id、Iq、θe确定为模型的输入参数,则输出参数为转矩Te*。融合模型在电机控制系统中的结构如图2所示。

图2 基于融合模型的转矩预测与电机控制原理

2.2 模型融合的结构设计

随着深度学习技术的发展,学者研究出很多人工智能神经网络模型[19-20]。采用结构简单、应用最广泛的BP和RBF两种神经网络来验证模型融合方法的有效性。BP和RBF神经网络是最常见的多层神经网络,其结构相似,但训练过程学习算法略有不同。基本结构如图3所示。

图3 多层神经网络的基本结构

网络结构分为输入层、隐含层、输出层,层与层之间通过神经元连接,各神经元之间的信息传递通过参数权值λ和偏置ν计算。神经网络训练过程是一种迭代过程,初始给定随机参数,在迭代计算过程中,通过评价函数判断是否达到训练要求,然后不断调整隐含层神经元的权值、阈值或神经元数等参数,直至达到要求。基于融合模型算法的神经网络训练流程如图4所示。

图4 融合模型算法训练流程

由式(4)可知,为了验证不同权值和偏置导致模型中的线性量对整体模型的适应性能,使用试凑法对这2个参数进行筛选。首先搭建传统BP神经网络,生成基本的融合模型。通过设置权值λ从0.2到1,梯度为0.2,偏置ν从-0.5到0.5,梯度为0.1,训练模型,得到不同参数对模型精度的影响结果,以模型预测均方误差为评价标准,为避免训练过程中出现偶然性,对参数多次测试,取结果方盒图的中位数进行比较,如图5、6所示。当权值λ为0.6,修正偏置ν为-0.1时,融合模型性能普遍最优。

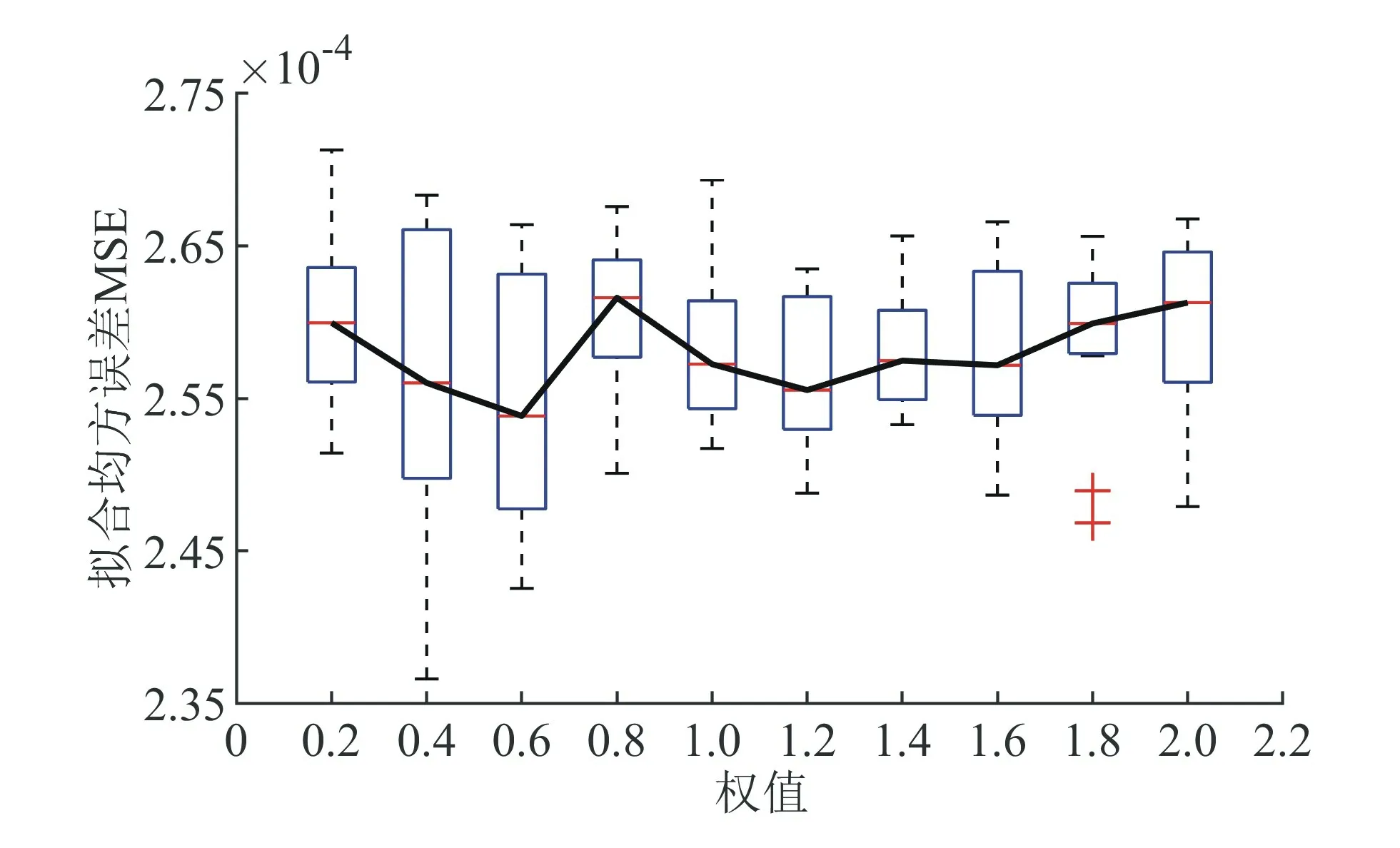
图5 不同权值对融合模型拟合性能的关系

图6 不同修正偏置对融合模型拟合性能的关系

2.3 基于模型融合方法的神经网络模型

神经网络模型的拟合性能受隐含层神经元数、学习率等参数影响。在神经网络模型的训练过程中,神经元数对网络的性能至关重要。但由于网络的参数选取没有相关合适的理论指导,并且模型参数对不同建模对象表现不同效果,因此,往往通过迭代方法对神经网络模型参数进行最优化设计。一般地,神经元个数过少,会导致模型拟合误差大,对动态变化的滤波效果差;而数量过多,模型易陷入局部最优解,模型训练及计算时间更长,对控制器计算力要求更高。因此,首先根据专家经验值选定数量区间,通过比较不同数量对模型拟合性能来筛选。

为了比较融合模型对网络结构的优化能力,将对2种网络中隐含层结构分别重新设计。首先,为了检验模型的实际应用效果,训练和测试数据均从实际控制系统中采集。因此,依据图2的转矩闭环控制系统,依次改变负载转矩,在10 k Hz的电机控制频率中采集Id、Iq、θe以及从转矩传感器中获得的Te数据共5万组,其中75%用于训练,25%用于测试。以同样的训练数据,设置隐含层神经元数从3到25,梯度为1,然后训练网络。以融合模型的均方误差为判断函数,并将训练结果与2种传统神经网络的效果进行对比,如图7、8所示。

图7 传统BP网络和基于融合方法的模型的拟合性能与神经元数关系

从图7可看出,相比传统BP神经网络模型,融合模型在隐含层神经元为10个时MSE就达到2.6×10-4水平左右,而传统BP神经网络需要25个以上神经元,这说明模型融合方法很大程度上减小了网络结构复杂度,也意味着网络模型计算量更少,更容易在普通嵌入式系统中实现模型计算。因此,在基于融合模型的BP网络结构设计中,取隐含层神经元的个数为10。

图8 传统RBF网络和基于融合方法的模型的拟合性能与神经元数关系

3 模型仿真与实验验证

3.1 模型仿真验证

通过采集不同转矩工况的样本数据,将训练好的基于融合方法的2种网络模型进行离线拟合测试,测试结果如图9～12所示。

图9 基于融合模型的BP网络转矩预测结果

图10 基于融合模型的BP神经网络转矩预测误差

图11 基于融合模型的RBF网络转矩预测结果

图12 基于融合模型的RBF网络转矩预测误差

从图9～12可知,融合模型的预测值与实际值误差基本小于0.05 N·m,在额定转矩时的转矩预测相对误差小于2.5%。这说明融合模型在降低网络结构复杂度的情况下,模型的实际预测精度依然保持很高,并且模型稳定性好。

3.2 转矩控制实验验证

为了验证模型在实际控制系统中的准确性和鲁棒性,将基于模型融合方法的转矩预测模型嵌入DSP平台的电机矢量控制系统中。由于神经网络计算量大,为了不影响电机控制周期,通过嵌入式系统的并行处理方式对转矩估算模型进行计算,数据通过DMA通道传输,方式如图13所示。

图13 转矩估算模型在DSP中的计算流程

对搭建的融合模型与传统网络模型实际计算时间进行测试。模型融合方法将传统BP网络需要25个神经元减少到10个,相应的DSP计算时间从84 μs减少为35μs。将传统RBF网络所需15个神经元减少为7个,相应DSP计算时间从51μs减少为25μs。因此,从实际优化效果看,可明显减少模型计算量,提高模型实际应用价值。为了验证模型在电机实际运行中预测的准确性,搭建了转矩预测控制硬件测试平台,如图14所示。

图14 电机转矩预测控制硬件验证平台

实验平台用三相电机作为负载,当实验电机旋转带动负载电机旋转,旋转速度越快,负载电机产生的反电动势越大,从而产生的负载转矩越大。在电机恒转矩控制时,当负载降低时,电机通过提高转速来维持转矩恒定,反之,会降低转速。因此,给定不同负载输出,观察电机转速响应和转矩变化,就可判断模型预测精度和动态性能。

分别对2种基于模型融合方法的神经网络转矩估算模型设定转矩1.0、1.5 N·m,不断改变负载,验证融合模型的无转矩传感器转矩估算与控制性能。图15、16为基于融合模型的BP网络转矩估算模型验证结果,图17、18为基于融合模型的BP网络转矩估算模型验证结果。

图15 变负载1.0 N·m恒转矩控制

图16 变负载1.5 N·m恒转矩控制

图17 变负载1.0 N·m恒转矩控制

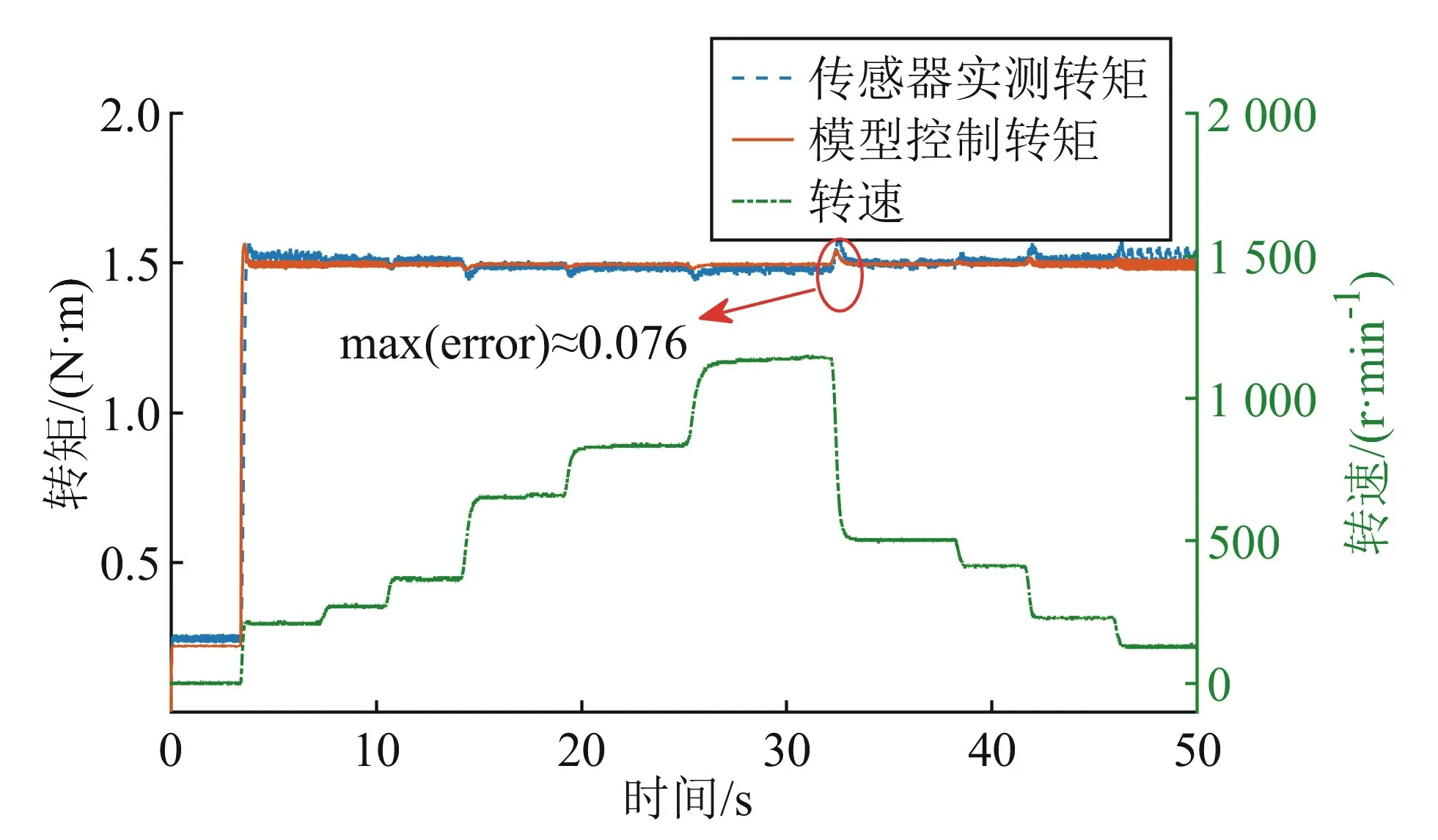
图18 变负载1.5 N·m恒转矩控制

从图15、16可知,在控制转矩为1.0 N·m 时,融合模型的动态控制性能最大误差约为0.057 N·m,估测偏差比真实测量转矩小5.7%。在控制转矩为1.5 N·m 时,最大误差约为0.054 N·m,估测偏差比真实测量转矩小3.6%。

从图17、18可知,控制转矩为1.0 N·m 时,融合模型的动态控制性能最大误差约为0.070 N·m,估算偏差比真实测量转矩小7%。控制转矩为1.5 N·m时,最大误差约为0.076 N·m,估算偏差比真实测量转矩小5.1%。

因此,基于模型融合方法的神经网络转矩估算模型具有较高的预测精度,模型抗干扰能力较好,验证了该模型的稳定性和准确性。

4 结束语

针对IPMSM 转矩模型中存在的非线性变化因素影响了转矩的估算性能,提出了一种模型融合方法,将传统数学模型与数据驱动的神经网络模型相融合,构成新的转矩估算融合模型。通过传统BP 与RBF网络模型对比的仿真和实验,证明了模型融合方法能有效降低传统神经网络对转矩建模的复杂度,并提高转矩估算精度,实现了无转矩传感器转矩高精度控制,为电机转矩智能控制领域提供了一条有效的新途径。