Vondrak滤波方法在软件接收机卫星双向时间传递中的应用*
王翔 宋会杰 郭栋 武文俊,3 董绍武,3
(1 中国科学院国家授时中心 西安 710600)
(2 中国科学院时间频率基准重点实验室 西安 710600)
(3 中国科学院大学天文与空间科学学院 北京 100049)
1 引言
作为协调世界时(Coordinated Universal Time, UTC)实现的主要技术手段之一, 卫星双向时间传递可以实现亚纳秒级的比对精度, 全球约有20多个时间保持实验室建立了TWSTFT (Two-Way Satellite Time and Frequency Transfer)链路,用于UTC的产生. 在UTC的计算过程中, TWSTFT链路负责传递约60%权重的原子钟数据以及大部分一级原子频标的数据. 然而, 传统TWSTFT链路存在明显的周日效应, 它是不确定度的主要来源[1]. 为了弱化周日效应对卫星双向链路时间传递效果的影响, 2016年国际权度局(Bureau International des Poids et Mesures, BIPM)组织开展了基于软件接收机的国际卫星双向时间传递(Two-Way Satellite Time and Frequency Transfer based on Software Defined Receiver, SDR-TWSTFT)比对试验, 发现SDR-TWSTFT链路在短基线链路比对中, 周日效应的影响降低了2-3倍, 在长基线链路中, 平均时间较小时显示出一定的测量噪声增益[2]. 2017年10月起, 依据21届国际时间频率咨询委员会(Consultative Committee for Time and Frequency, CCTF)大会的决议, 基于软件接收机的卫星双向时间传递链路成为UTC时间传递链路的备份链路.
关于SDR-TWSTFT链路的性能及其改进方法的分析讨论是当前研究的热点之一, 研究主要集中于亚洲和欧洲洲际内以及欧亚和欧美洲际间的卫星双向链路. 一方面可以利用冗余的TWSTFT链路形成间接链路, 通过抑制频带间干扰达到改善性能的目的[3]; 另一方面可以构建平差网络, 通过分摊网络中各链路测量噪声, 提高被优化链路性能[4-5].
2018年3月亚欧实验室之间通过俄罗斯的ABS-2A卫星重建了Ku波段的卫星双向时间传递链路. 本文根据SDR-TWSTFT链路的特殊性能,针对性地提出了频域幅值法, 用于选择Vondrak滤波[6]因子, 先通过合适的滤波因子对SDRTWSTFT链路时间传递结果进行低通滤波抑制高频分量, 再利用GPS (Global Positioning System) PPP (Precise Point Positioning solutions)时间传递链路数据评估滤波效果, 最后分析滤波前后SDR-TWSTFT链路性能.
2 SDR-TWSTFT链路校准
2.1 SDR-TWSTFT原理
如图1所示, SDR-TWSTFT与传统卫星双向时间传递系统在信号发射段结构相同. 地面站A通过调制解调器(SAtellite Time and Ranging Equipment, SATRE)的发射通道把与主钟信号同步的伪随机码(Pseudorandom Noise, PRN)通过二进制相移键控(Binary Phase Shift Keying, BPSK)的方式调制到中频载波上[7], 再通过上变频器把中频信号调整至Ku波段, 经甚小口径终端(Very Small Aperture Terminal, VSAT)发射到地球同步卫星(Geosynchronous Earth Orbit, GEO), GEO卫星透明转发地面站A的时间信号. 地面站B实时接收经GEO卫星转发的地面站A的时间信号, 通过下变频器把Ku波段信号调整至中频, 在接收段与传统卫星双向时间传递系统相比, 增加了SDR设备, 对中频信号解调后, 与B站主钟信号相互比对, 获得单边时间传递结果. 地面站A、B交互数据, 利用卫星双向时间传递结果计算方法, 获得两站主钟钟差. 卫星双向时间传递结果计算公式如下:
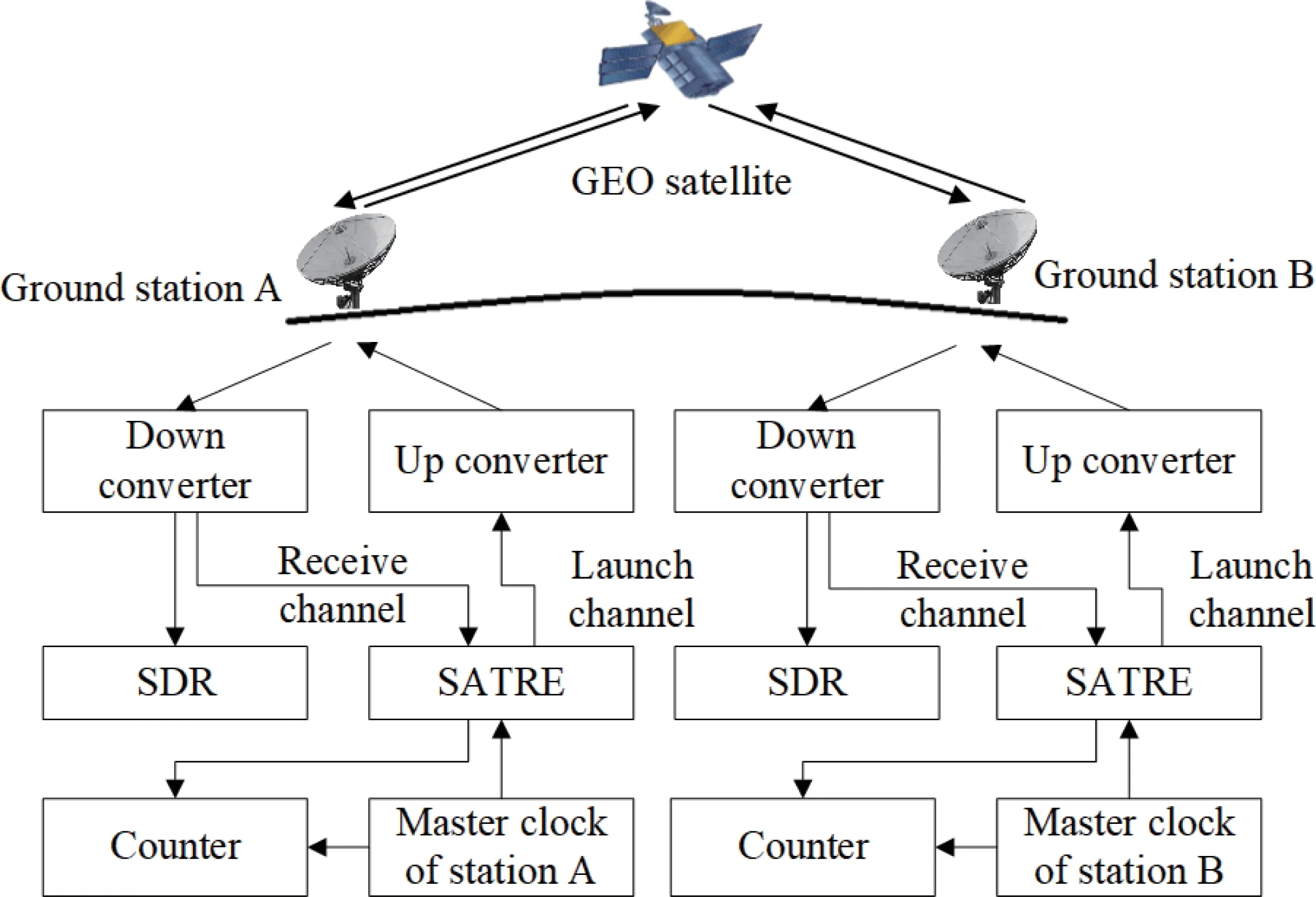
图1 SDR-TWSTFT链路系统结构Fig.1 Structure of SDR-TWSTFT link

其中Tk为地面站主钟钟面时,k为地面站代号(后同),TTWk为地面站测得的单边传输时延,TCALRk为卫星双向时间传递中的标定时延,TESDVARk为标定时延后地面站时延修正值,TREFDLYk为地面站本地时间参考点至卫星双向时间传递设备之间的时延.
2.2 SDR-TWSTFT链路校准方法
为了提高卫星双向时间传递的准确度, 需要对链路进行校准. 自从1997年Zumberge等人提出GPS PPP算法[8]以来, 通过不断优化误差修正模型[9-15], 目前轨道精度已达2.5 cm, 钟差精度优于0.1 ns[16-17], 电离层、固体潮等相关物理模型的优化, PPP的A类时间传递不确定度已达100 ps[18-20].由于GPS PPP具有高分辨率、高精度的特点, 当没有校准器可以实施直接校准的时候, 对于全球卫星导航系统(Global Navigation Satellite System,GNSS)时间传递链路的校准能够转移到双向链路,可以用校准过的GNSS链路校准双向链路.
使用已校准的GPS PPP链路对SDRTWSTFT链路进行校准[21-23]的原理如图2所示.本地相位微调仪输出的UTC(k)的物理实现信号分别是1PPS(Pulse Per Second)脉冲和5 MHz频率信号. 通过倍频器将频率信号变换为10 MHz, 供已校准接收机、待校准SDR设备使用. 使用相位微调仪输出的1PPS脉冲信号作为本地已校准GPS PPP链路中的接收机、待校准TWSTFT链路中的调制解调器的初同步秒信号, PTB的连接类同, 在本地实验室与PTB之间采用同源信号, 使用GPS PPP和SDR-TWSTFT原理, 建立两条独立的时间传递链路. 对于GPS PPP链路, 测量得到UTC(k)与IGS系统时间(International GNSS Service Time,IGST)的偏差, 通过数据传输网络交互各自的测量结果数据,得到UTC(k)与UTC(PTB)的钟差DPPP.对于SDR-TWSTFT链路, 依据前一小节所述SDRTWSTFT原理, 测得单边数据后, 通过数据传输网络交互数据, 得到UTC(k)与UTC(PTB)的钟差DSDR-TWSTFT. 将DSDR-TWSTFT时间序列以DPPP的时标为参考进行插值[24], 得到DCPPP.DCPPP与DSDR-TWSTFT之差即为单次校准值, 记为C=DCPPP-DSDR-TWSTFT. 校准值即为单次校准值的平均值. 为了提高校准值的准确度, 我们至少需要7 d的连续测量数据.
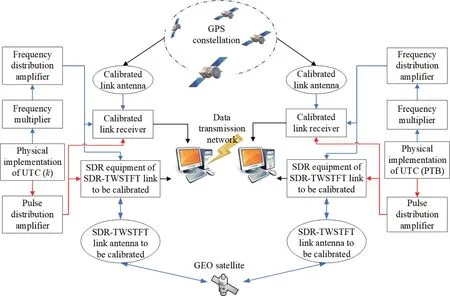
图2 SDR-TWSTFT链路校准原理Fig.2 SDR-TWSTFT link calibration principle
3 Vondrak滤波方法
Vondrak滤波能够在不知道测量数据变化规律的条件下, 通过确定合适的滤波因子, 在测量数据的绝对拟合和绝对平滑之间寻求一条折中的曲线[6].
3.1 基本原理
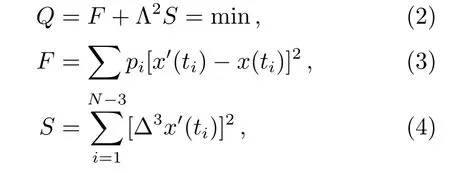
记测量数据为x(ti), 其中i= 1-N,N为自然数. Vondrak滤波基本公式[25]如下:其中, Λ2为待定系数, 用于调整拟合度与平滑度的关系;F为Vondrak滤波的拟合程度;S是对滤波值3次差分平方和的约束条件, 体现了滤波曲线的平滑度;x′(ti)为滤波值,pi为x(ti)的权重. 当Λ2→0时, 需要F →0才能使Q取得最小值, 反之, 当Λ2→∞时, 需要S →0才能使Q取得最小值.
3.2 确定滤波因子
目前UTC(NTSC)的日稳定度在10-15量级, 长期的数据统计分析结果表明, NTSC卫星双向时间传递的长期稳定度在10-15量级, 1 d以内的中短期稳定度在10-14-10-13之间. 时间传递链路引入的测量不确定度是UTC(k)计算时不确定度的主要来源. 为了提高UTC(NTSC)的时间传递精度, 本文采取频域幅值分析方法选择滤波因子.
SDR-TWSTFT链路的测量过程中, 采样时间间隔短, 环境噪声对测量结果短期稳定度的影响比较明显, 因此在后期数据处理过程中, 需要在抑制短期噪声的同时, 保留信号中长期特征. 我们着重分析了在不同滤波因子下, 滤波结果分别在48、36、24、12、8、6、4、2 h的幅值曲线. 选择能够使48、36 h的频域幅值尽量高, 24、12、8、6、4、2 h的幅值尽量低的因子对测量数据进行滤波.
4 比对结果与性能分析
本文选择约化儒略日(MJD) 59130-59160之间共30 d的数据进行分析. 首先对SDR-TWSTFT测量结果采取中位数法进行粗值剔除后, 使用GPS PPP测量结果对SDR-TWSTFT测量结果进行校准,接着使用3.2节所述方法选择Vondrak滤波因子,再以GPS PPP测量结果作为评估标准, 计算滤波前后数据与评估标准之间的标准差, 分析了滤波结果的准确度, 最后对比了滤波前后时间传递结果的稳定度.
4.1 NTSC-PTB的SDR-TWSTFT链路校准结果
图3是滤波前后NTSC-PTB的SDR-TWSTFT测量结果与GPS PPP链路和BIPM公报之间的比对结果, 滤波前后SDR-TWSTFT链路测量结果与GPS PPP链路测量结果和BIPM的Circular T公布数据趋势基本相符.
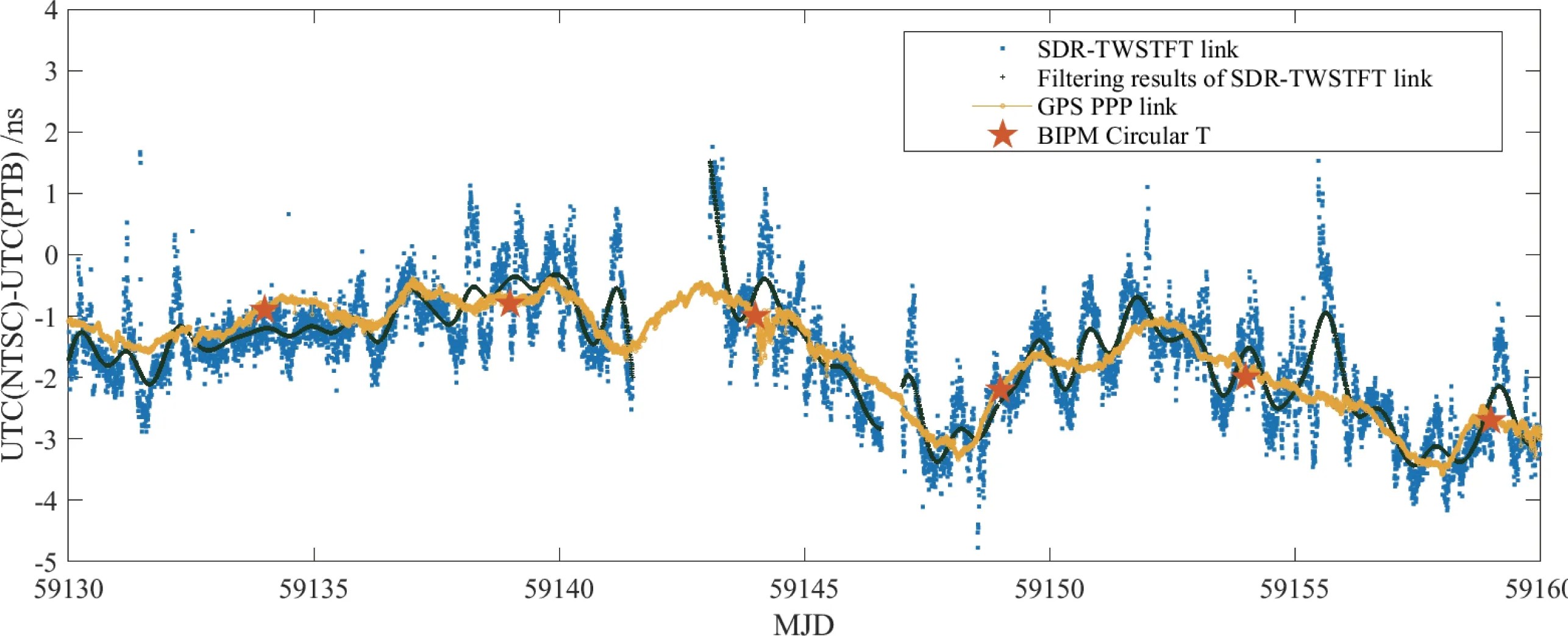
图3 NTSC-PTB的SDR-TWSTFT链路滤波前后链路测量结果与Circular T比较Fig.3 Comparison of NTSC-PTB SDR-TWSTFT link before and after filtering with Circular T
根据测量不确定度传播率, 两条相互独立的链路测量不确定度平方和的算术平方根是链路间的合成不确定度, 当两条链路测量结果的最大偏差处于不确定度范围内时, 两链路测量结果具备一致性.NTSC-PTB SDR-TWSTFT链路滤波前的测量不确定度[26]约1.59 ns, NTSC-PTB GPS PPP链路的测量不确定度约1.48 ns. SDR-TWSTFT链路与GPS PPP链路的最大偏差的绝对值应小于2.17 ns.图4是滤波前后NTSC-PTB的SDR-TWSTFT链路与GPS PPP链路最大偏差分布图, 测量噪声的关系使得滤波前两条链路的一致性较差, 滤波后两条链路的最大偏差处于不确定度范围之内, 链路测量结果一致.
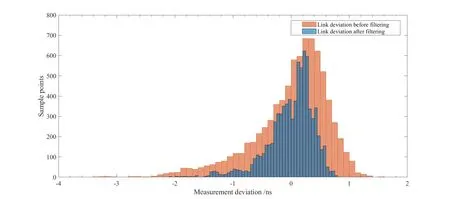
图4 NTSC-PTB的SDR-TWSTFT链路滤波前后链路间最大偏差分布Fig.4 Distribution of maximum deviation between NTSC-PTB SDR-TWSTFT link before and after filtering
4.2 滤波因子选择实例
Vondrak滤波在滤波因子越小, 滤波后数据越平滑, 在处理SDR-TWSTFT链路数据时, 先使滤波因子在0-50000范围内, 以100为步长对数据进行滤波, 再对滤波结果进行频谱分析, 发现滤波因子小于5500时, 链路24 h内的特性失真很大, 不符合需求. 因此设置滤波因子处于5500-15005500之间,以1000为步长对校准后的SDR-TWSTFT测量数据进行Vondrak滤波. 图5是采用不同滤波因子滤波后, 不同时间间隔下, 滤波结果在频域的幅值曲线.显然在滤波因子处于505500-3005500之间时, 各个时间间隔对应的频域幅值曲线均单调上升. 为了在抑制测量结果24 h内的高频噪声的同时保留测量结果的低频特征, 选择24 h与48 h频域幅值曲线交点处对应的滤波因子对原始测量数据进行滤波. 交点处横坐标为ε=2225500.
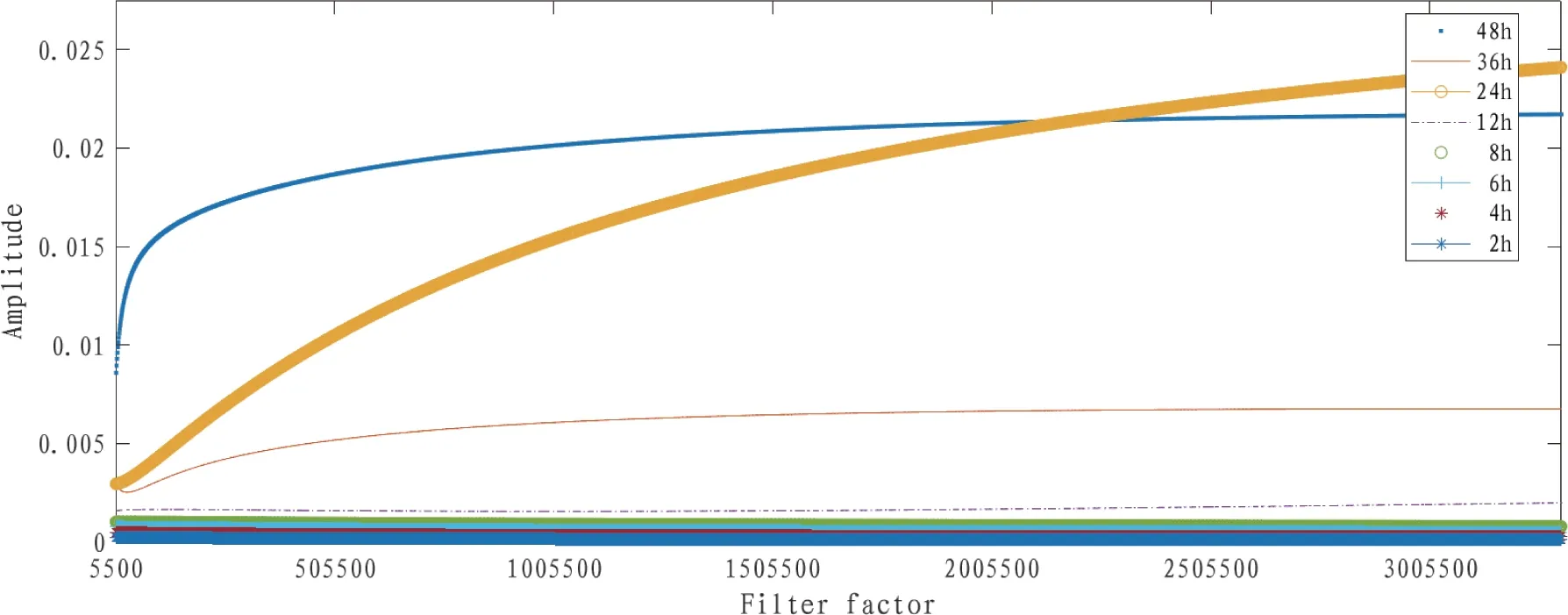
图5 NTSC-PTB的SDR-TWSTFT链路滤波因子选择Fig.5 Selection of filter factors for NTSC-PTB SDR-TWSTFT link
4.3 链路性能分析
4.3.1 稳定度分析
图6是滤波前后NTSC-PTB SDR-TWSTFT链路的Allan方差分析结果, 虚线为滤波前, 实线是滤波后, Tau为平均时间. Vondrak滤波后链路频率稳定度如表1所示, 可以看到在平均时间处于2560 min内的链路频率稳定度均有所提高, 平均时间5 min的短期稳定度提高约87%, 平均时间1280 min的短期稳定度提高约42%.
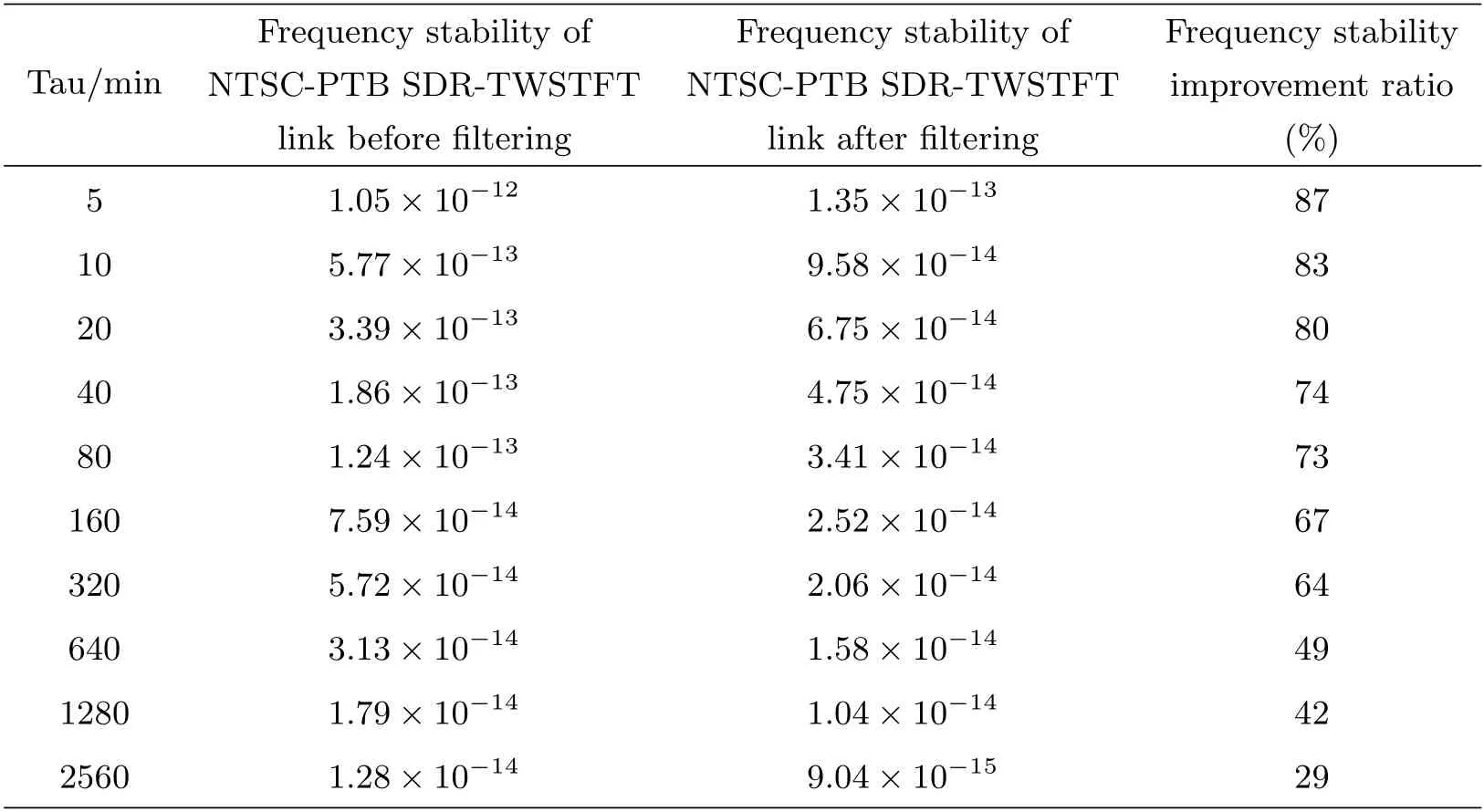
表1 NTSC-PTB的SDR-TWSTFT链路滤波前后频率稳定度分析Table 1 Frequency stability analysis of NTSC-PTB SDR-TWSTFT link before and after filtering
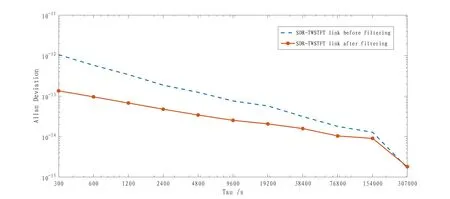
图6 NTSC-PTB的SDR-TWSTFT链路滤波前后Allan方差分析Fig.6 Allan deviation analysis of NTSC-PTB SDR-TWSTFT link before and after filtering
图7是滤波前后NTSC-PTB SDR-TWSTFT链路的时间方差(TDEV)分析结果, 虚线为滤波前,实线是滤波后. Vondrak滤波后链路时间稳定度如表2所示, 可以看到在平均时间处于2560 min内的链路频率稳定度均有所提高, 平均时间5 min的短期稳定度提高约87%, 平均时间1280 min的短期稳定度提高约4%.
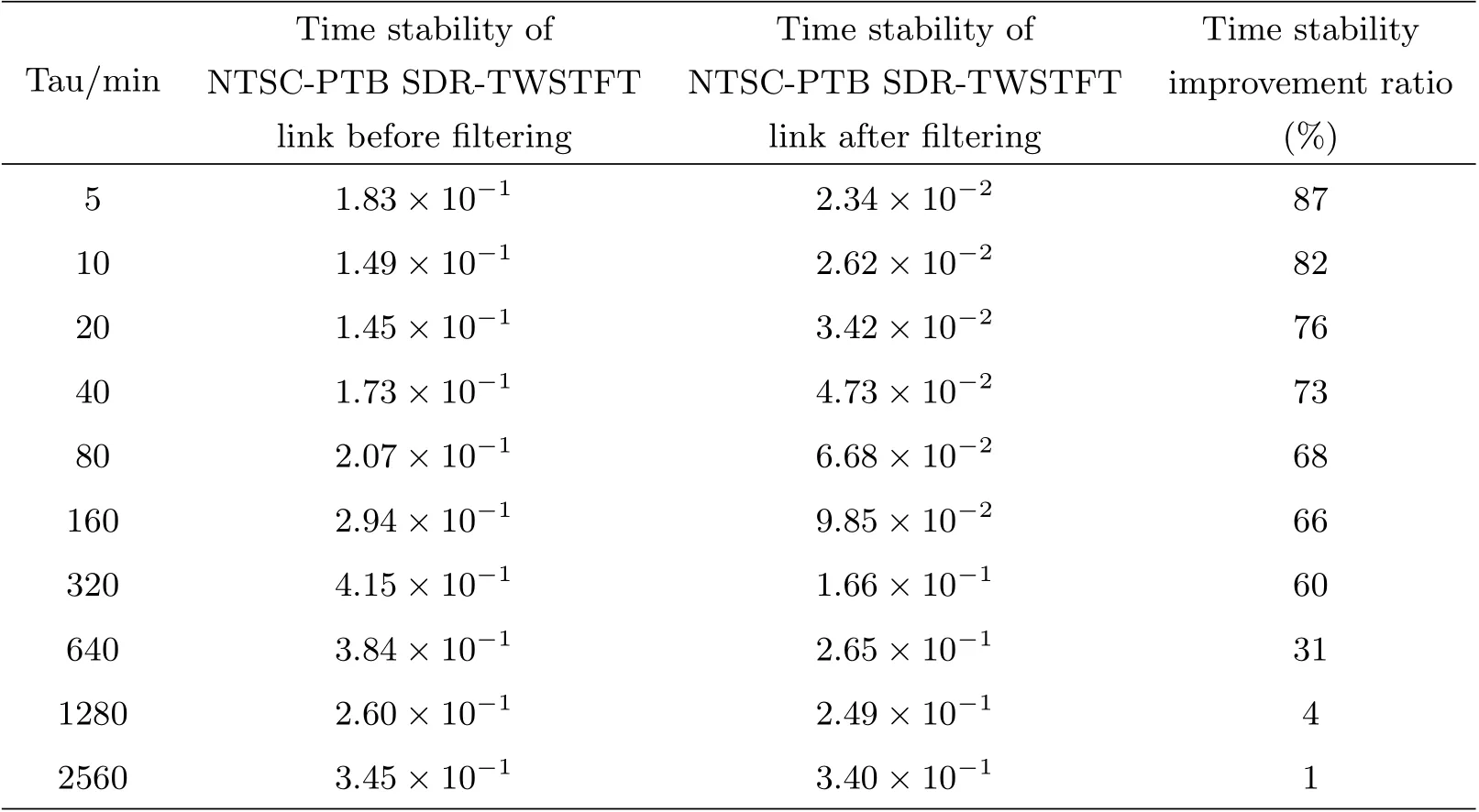
表2 NTSC-PTB的SDR-TWSTFT链路滤波前后时间稳定度分析Table 2 Time stability analysis of NTSC-PTB SDR-TWSTFT link before and after filtering
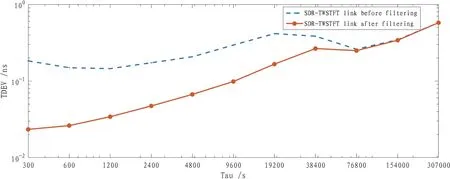
图7 NTSC-PTB的SDR-TWSTFT链路时间方差比较Fig.7 The TDEV comparison of NTSC-PTB SDR-TWSTFT link
上述稳定度分析结果表明, Vondrak滤波器可以有效地滤除链路测量数据中的高频噪声. 使用频域幅值法确定的滤波因子滤波后, 滤波结果在1 d内的短期频率稳定度和时间稳定度方面都有较好的表现.
4.3.2 谱分析
下面我们利用频谱分析对时间链路传递结果的各个频率分量进行量化分析. 图8是NTSC-PTB SDR-TWSTFT链路滤波前后的频域幅值谱, 蓝色是滤波后的谱分析结果, 红色是滤波前的谱分析结果. 滤波后信号的总能量是减小的, 但因为在画图时, 进行了归一化处理, 所以滤波前后图中标注出的24 h分量相对于各自的总能量呈现出了滤波前能量小、滤波后能量大的现象. 我们关注的是滤除高频分量后, 能量分布向低频段集中. 使用3.2节中的滤波因子选择方法滤波后, 时间传递结果中的高频分量得到了明显抑制, 低频分量特征也表现得更加明显.
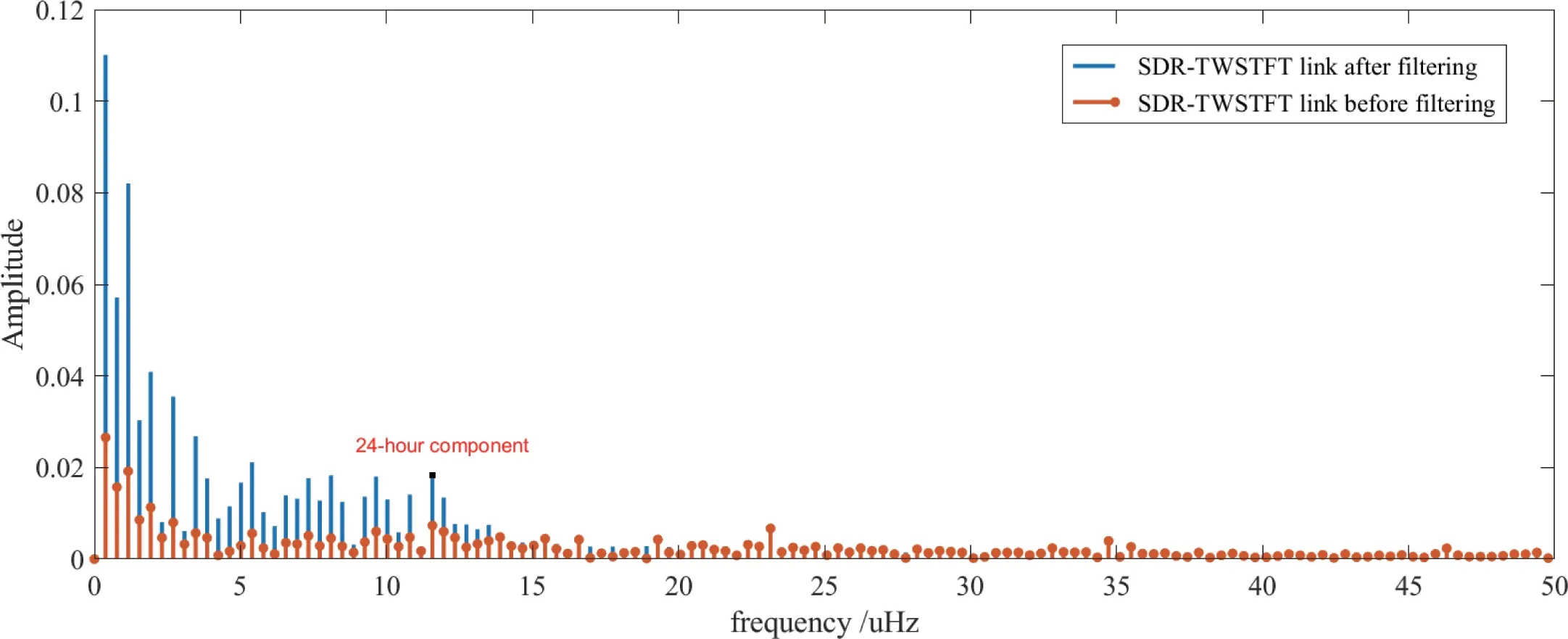
图8 NTSC-PTB的SDR-TWSTFT链路滤波前后谱分析Fig.8 Spectrum analysis of NTSC-PTB SDR-TWSTFT link before and after filtering
5 结论
SDR-TWSTFT于2020年2月正式用于UTC和国际原子时(International Atomic Time, TAI)的计算, 是国际时间传递中时间传递性能最高的技术手段之一, 它的日频率稳定度和时间稳定度分别可以达到10-15和1 ns量级. 为了进一步提高它的短期稳定度, 本文使用Vondrak滤波方法, 尝试通过滤除高频噪声的方式达到提高时间传递结果短期稳定度的效果. 首次使用频域幅值法选取滤波因子, 实现对时间传递结果的低通滤波. 使用本文介绍的方法处理分析NTSC-PTB的SDR-TWSTFT链路实测数据得出以下结论:
(1) Vondrak滤波方法可以有效滤除测量结果中的高频噪声, 不仅能够提高SDR-TWSTFT时间传递链路的短期频率稳定度, 还能改善链路的短期时间稳定度;
(2)使用频域幅值曲线选择滤波因子, 可以根据实际需求, 灵活选择符合条件的滤波因子. 该方法对过滤SDR-TWSTFT链路平均时间一天内的高频噪声有效, 在滤除噪声的同时, 保留了测量数据的低频特征分量;
(3)通过对比滤波前后SDR-TWSTFT链路与GPS PPP链路的残差分布,滤波后测量结果分布于链路测量不确定度范围以内, 该方法提高了SDRTWSTFT链路时间传递结果的可信度.

