基于单目视觉的天线副面并联调整机构相对位姿测量方法*

张文哲 项斌斌 王娜 王兆军 古丽加依娜哈再孜汗，3

(1 新疆大学物理科学与技术学院 乌鲁木齐 830046)

(2 中国科学院新疆天文台 乌鲁木齐 830011)

(3 中国科学院大学 北京 100049)

1 引言

在天文领域， 射电望远镜通常采用六自由度(6-DOF)并联机构[1-2]调整天线副面位姿， 为了能够提高天线副面并联调整机构的控制精度， 需要精准测量六自由度并联机构动平台的位姿. 目前， 对六自由度并联机构主要是通过传感器[3]或激光跟踪仪[4]来检测其动平台位姿， 而单目视觉测量系统仅需使用一台相机解算单幅图像的位姿信息， 与其他视觉测量系统相比， 具有结构简单、测量范围大、相机标定简单等优点， 避免了立体匹配的困难， 广泛应用于自动导航、机器人跟踪、飞行器对接等多个领域[5].

六自由度并联机构动平台的相对位姿解算是单目视觉位姿测量系统的核心， 解算的准确度越高， 相对位姿测量越精确， 对此研究者们提出了很多位姿解算方法. 其中最常用的单目视觉位姿解算方法是基于特征点的位姿解算方法， 即n点透视(Perspective-n-Point， PnP)问题， 其中n为特征点的个数[6]. Fischler和Bolles于1981年首次提出PnP问题[7]. Quan等人提出了一种针对4个点和5个点的情形， 构成一个P3P问题利用Singular Value Decomposition (SVD)分解的解算算法， 拓展到n个点的线性解算方法[8]. SVD算法容易受误差影响， 当误差较大时算法精度会迅速下降. 霍炬等人以平面P4P几何为约束条件， 采用改进的两段式迭代算法解算位姿， 并给出了特征标靶最优布局， 以获得更高的测量精度[9]. 张世杰等人利用目标航天器本身的特征信息， 采用P3P问题的解析方法获得迭代初值， 再采用Levenberg-Marqurdt(LM)算法最终迭代出目标的相对位姿[10]. 这种方法的最终解算精度与初值选取有关， 需确保初值选取的准确性， 否则算法可能会不收敛或收敛到错误的位姿导致无法使用. Lepetit等人于2009年提出了非迭代高精度快速位姿估计算法-EPnP (Efficient Perspective-n-Point)算法[11]， 该算法具有时间复杂度低、计算量相对较小等特点， 被认为是目前最高效的位姿估计算法之一. 武君等人为了分析POSIT (Pose from Orthography and Scaling With Iteration)与EPnP两种算法的优缺点， 通过大量实验， 从特征点数、噪声、实时性等方面进行对比，结果显示EPnP算法的测量精度高，POSIT算法的求解速度快[12]. 分析得出， 对于PnP问题， 算法的解算精度与特征点坐标提取精度有关， 坐标提取精度越高， 位姿解算精度越高.

为了快速精准测量六自由度并联机构动平台的位姿， 本文提出了一种基于非共面合作目标和EPnP算法结合的单目视觉位姿测量方法. 文章内容安排如下: 首先介绍了并联机构位姿的测量方案， 然后对EPnP算法和平方加权质心法进行了描述， 通过特征点在三维空间坐标系和二维图像坐标系之间的对应关系和空间位置约束， 解算出并联机构的相对位姿， 最后通过单目视觉位姿测量实验验证了本方法的精度和有效性.

2 六自由度并联机构相对位姿测量方案

本文采用单目视觉技术对六自由度并联机构动平台位姿进行实时测量， 测量系统如图1所示， 合作目标固定于动平台上， 相机固定于静平台上， 动平台相对于静平台的运动等效于合作目标相对于相机的运动. 当动平台运动时， 相机实时拍摄动平台上合作目标的图像， 然后采用单目视觉技术得到动平台的位姿. 该测量系统的工作原理是控制安装于相机顶部的照明单元对合作目标进行照明， 合作目标上各高反标志点将入射光准原路反射回去之后进入相机视场成像， 对图像进行特征处理后， 提取出有效的合作目标信息， 再采用位姿解算算法获得动平台相对位姿信息.

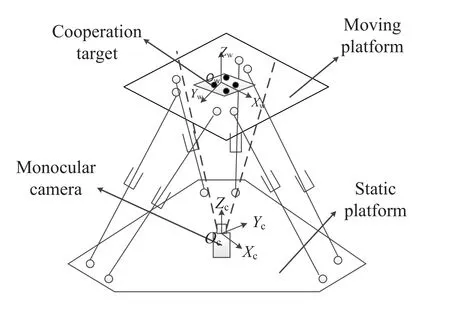
图1 单目视觉测量系统示意图Fig.1 Schematic diagram of the monocular vision measurement system

并联机构相对位姿测量流程如图2所示， 主要测量过程如下:

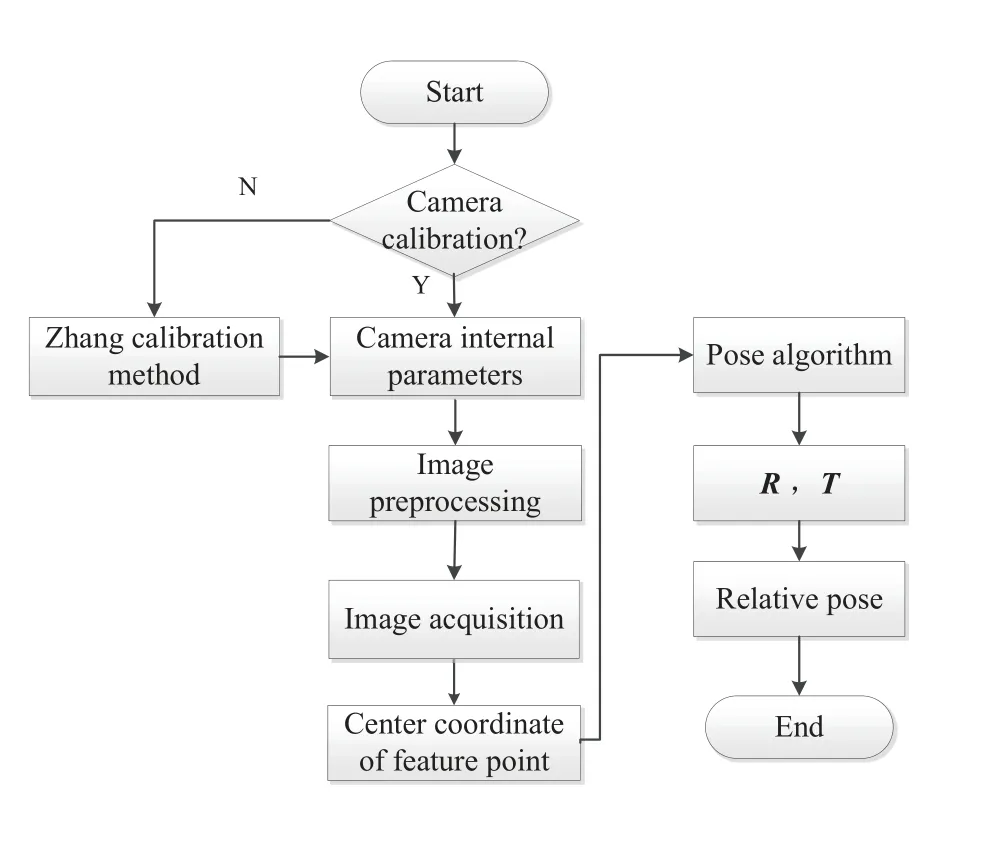
图2 系统流程图Fig.2 System flow chart

(1)图像采集和相机标定

控制照明单元对合作目标进行照明， 采集合作目标运动图像， 采用张正友标定法[13]获得相机内部参数.

(2)图像预处理和图像特征提取

对图像进行去噪处理、灰度二值化、阈值分割等操作， 再采用平方加权质心法[14]提取特征点图像中心坐标.

(3)单目视觉位姿解算

采取EPnP算法对特征点图像中心坐标进行位姿解算， 通过与多个非共面特征点结合的方法降低图像噪声的影响并提高算法的抗干扰能力. 该算法的核心思想是利用三维线性空间的一组基(4个非共面虚拟控制点)线性加权表示空间三维特征点，把求解n个特征点在相机坐标系下的坐标转换为求解4个虚拟控制点在相机坐标系下坐标的问题， 从而降低了算法的复杂度[15]， 然后通过Horn等人提出的绝对定位算法[16]求解合作目标相对于相机的旋转矩阵R和平移向量T.

3 单目视觉位姿测量原理

3.1 单目视觉位姿测量模型

本文所采用的单目视觉位姿测量方法是用单个相机拍摄合作目标图像， 经过上述位姿测量流程， 最终解算出目标坐标系相对于相机坐标系的姿态和位置信息. 采用的相机成像模型是针孔成像模型[17]， 该成像模型需要建立4个坐标系， 分别是目标坐标系、相机坐标系、图像物理坐标系以及图像像素坐标系， 坐标系之间的关系如图3所示. 以合作目标上某一特征点为原点， 建立目标坐标系Ow-XwYwZw， 跟随合作目标一起运动; 以相机的光心为原点， 以光轴为Zc轴， 建立相机坐标系Oc-XcYcZc; 图像坐标系所在平面为相机的成像平面， 建立图像物理坐标系O-xy和图像像素坐标系O0-uv. 图中Oc、f、Zc分别为相机的光心、焦距、光轴，C1、C2、C3、C4代表虚拟控制点， 以黑点表示特征点，P为其中之一.

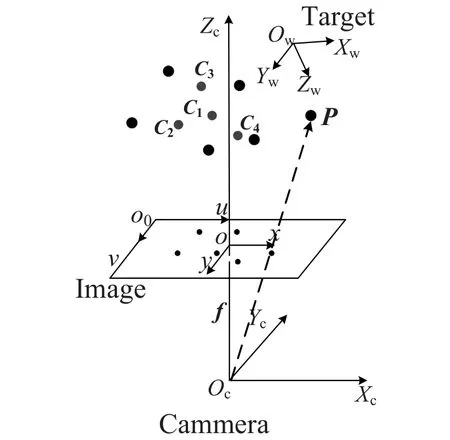
图3 单目视觉位姿测量原理Fig.3 The principle of monocular vision pose measurement

设点P在相机坐标系下的坐标为(Xc，Yc，Zc)，在目标坐标系下的坐标为(Xw，Yw，Zw)， 在图像像素坐标系下的图像坐标为(ui，vi)， 经过标定获得相机的内参矩阵为A， 图像主点坐标为O0= (u0，v0)，则P点在彼此坐标系下的关系为:

3.2 位姿解算算法

EPnP算法中4个虚拟控制点一般是人为选取， 通常情况下，C1为特征点集的质心，C2、C3、C4为特征点集主分量分解后的3个分量.

通过(7)式和(8)式求出ξ值和X值， 即可得到4个虚拟控制点在相机坐标系下的坐标. 通过(3)式得到特征点在相机坐标系下的坐标， 从而将求解三维到二维的PnP问题变换为求解经典的三维到三维的刚体运动问题， 最后通过Horn绝对定位算法得到合作目标相对于相机的姿态角和平移量.

3.3 图像特征点中心坐标的提取

由上述位姿解算算法可知， PnP问题的求解主要依靠标定过的特征点的空间相对位置和图像特征点的坐标， 所以位姿的测量精度直接取决于图像特征点的中心定位精度.

为了提高特征点的定位精度， 合作目标选用非共面高反标志点和滤光片， 相机镜头也安装了相同的滤光片. 为了利用特征点z方向上的信息选择非共面的合作目标特征点， 可以更好地检测出合作目标的微小转动. 测量过程中通过光源照射合作目标， 得到反射光斑， 获得高对比度的准理想图像， 从而降低光源的影响， 并简单有效地划分了图像特征区域. 本文选用平方加权质心法对图像特征点中心坐标进行提取. 设f(x，y)为二维灰度图像中位于坐标位置(x，y)的像素点的灰度值，m代表像素点，0＜x ＜mj， 0＜y ＜mj， 则其数学描述如下:

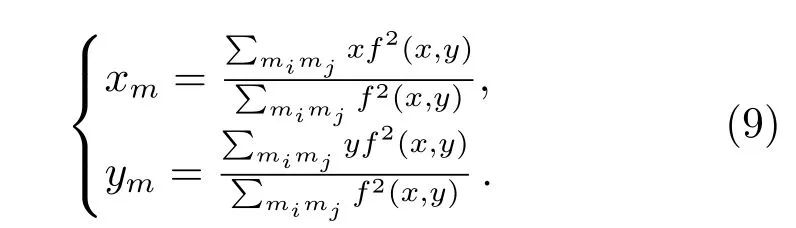
平方加权质心法采用灰度值的平方作为权值， 加强了距离中心较近的像素点对质心的影响， 减少了噪声带来的误差. 最后将提取出的中心坐标代入位姿解算算法中， 得到合作目标与相机之间的姿态和位置信息.

4 实验和结果分析

4.1 实验描述

为了检验位姿测量方法的精度， 搭建了六自由度并联机构单目视觉位姿测量实验平台， 六自由度并联机构如图4所示， 实验平台如图5所示， 主要由相机探测单元和合作目标组成. 相机探测单元中相机采用一体化设计， 光学镜头、成像探头、数据处理电路、照明电路等组件均在同一机箱内; 相机的分辨率为2592× 2048， 镜头焦距16 mm. 合作目标由7个圆形高反射率标志和滤光片组成， 以一定构型安装在支架上， 其中6个标志点位于底面直径为140 mm的同一圆周上， 第7个特征点位于正中央，相对其他6个点有60 mm的高度差. 相机和合作目标如图6所示; 实验中相机拍摄合作目标， 处理过的图像如图7所示.

图4 六自由度并联机构Fig.4 6-DOF parallel mechanism

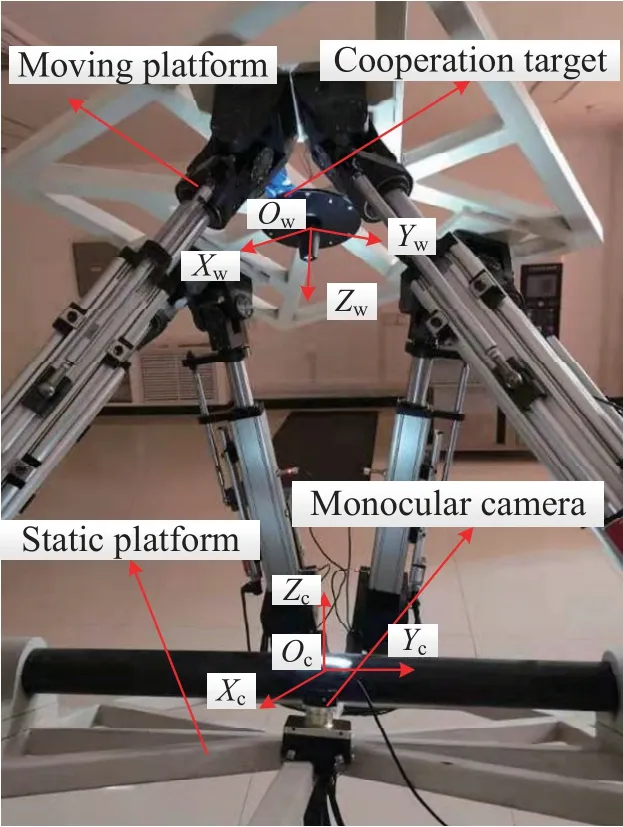
图5 实验平台Fig.5 Experimental platform

图6 相机和合作目标Fig.6 Camera and cooperation target

图7 特征点图像处理图Fig.7 Image processing chart of feature points

相对位姿的测量包括目标坐标系沿相机坐标系的x轴、y轴、z轴的平移距离和旋转角度， 其中绕x轴旋转得到α， 绕y轴旋转得到β， 绕z轴旋转得到γ.

4.2 结果分析

通过改变六自由度并联机构动平台的平移距离和旋转角度， 将合作目标相对于相机的位置和姿态参数作为测量值， 然后拍摄图像测试方法的有效性. 以垂直于相机光轴位置为零位， 选择的平移范围为±30 mm，依次沿x、y、z轴平移5 mm;旋转范围为±5°， 依次沿x、y、z轴旋转1°. 将测量值与理论值进行比较， 得到平移距离和旋转角度的位姿测量误差曲线， 结果如图8所示; 对图8进行数据分析，分别得到平移距离误差表和旋转角度误差表， 如表1和表2所示. 均方根误差(RMSE)表示的是测量值与真实值之间的偏差， 代表着测量值相对于平均值的离散程度， RMSE越小代表着数据越聚集， 通常情况下， RMSE越小测量精度越高.

由表1和表2数据可得， 各方向上的最大误差和RMSE分别为:x方向0.0440 mm和0.0232 mm;y方向0.0838 mm和0.0325 mm;z方向0.0938 mm和0.0672 mm;α方向0.0333°和0.0146°;β方向0.0280°和0.0159°;γ方向0.0221°和0.0090°. 由图8可知， 当动平台偏离静平台时， 沿x轴和y轴的平移和旋转方向上的测量误差呈现相对增大趋势， 主要原因是合作目标逐渐偏离相机的测量范围， 降低了图像点的提取精度， 从而使图像处理误差增大; 沿z轴平移方向上的测量误差从零位开始逐渐增大， 相对于其他方向的误差，z方向较大， 主要原因是动平台的抖动和景深增大， 前者在动平台沿z轴上下移动时导致合作目标偏离原本固定于动平台的位置， 使得解算出来的位姿出现误差， 而后者降低了图像点的提取精度; 但沿z轴的旋转误差相对较小， RMSE也较小， 主要由于水平转动不影响图像处理精度. 由实验数据可知， 相机与合作目标间平移±30 mm范围内， 测量误差小于0.1 mm. 旋转±5°范围内， 测量误差小于0.05°， 该测量精度满足六自由度并联机构的精度要求.

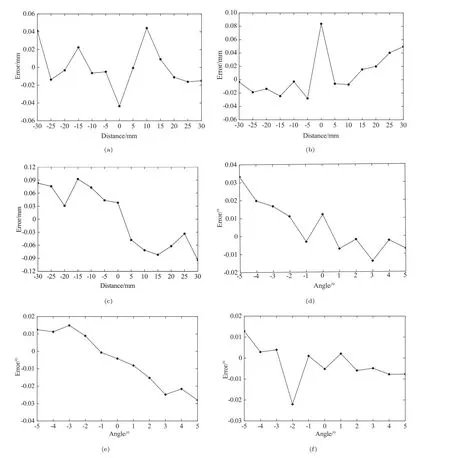
图8 位姿测量误差: (a) x轴平移误差; (b) y轴平移误差; (c) z轴平移误差; (d) α旋转角误差; (e) β旋转角误差; (f) γ旋转角误差.Fig.8 Pose measurement error: (a) translation error of x-axis; (b) translation error of y-axis; (c) translation error of z-axis; (d)the rotation angle error in α direction; (e) the rotation angle error in β direction; (f) the rotation angle error in γ direction.

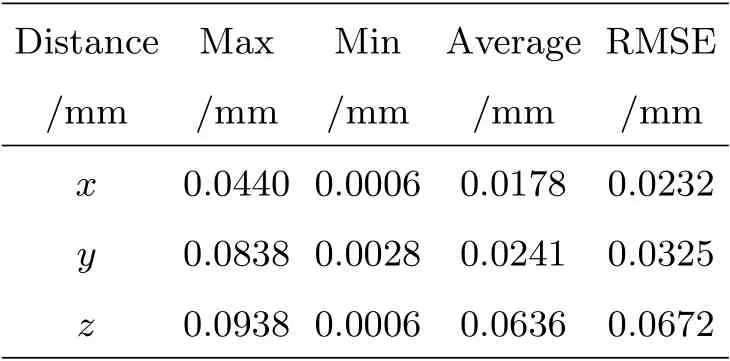
表1 平移距离测量误差Table 1 Translational distance measurement error

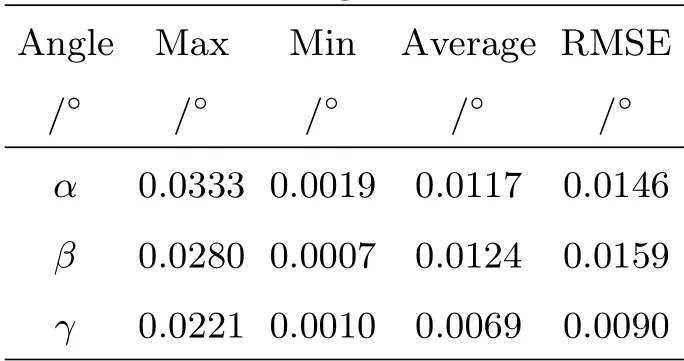
表2 旋转角度测量误差Table 2 Rotation angle measurement error

实验中除了因为环境、设备、图像处理和算法解算等因素引起的测量误差外， 合作目标的制作精度也可能会带来误差， 制作时合作目标上特征点之间的真实距离与给定的理论距离的差值会带来特征点坐标的误差. 因此， 想要进一步提高位姿测量精度， 需要对测量误差的来源进行分析， 如可采用精度更高的相机及合作目标提高图像处理精度，保证合作目标紧紧地固定在动平台上， 或通过增加特征点的个数提高测量精度， 特征点越多测量精度越高. 一般需要根据被测物体的结构尺寸、实时性、精度等要求选择适当数量的特征点， 因为太多会增大图像处理和位姿解算算法的运算时间和复杂度， 而特征点太少的话， 当在相机拍摄合作目标运动图像过程中， 合作目标上的特征点可能会发生遮挡或丢失等情况导致提取的特征点个数不足， 影响测量精度.

5 结论

为实时检测六自由度并联机构动平台的位姿，本文提出了一种基于非共面合作目标与EPnP算法结合的单目视觉位姿测量方法， 该方法通过获得的高对比度图像和提取出的高精度中心坐标，再采用EPnP算法对动平台的位姿进行求解. 通过样机研制与实验测试可知， 并联机构动平台在平移±30 mm范围内， 沿x、y、z轴方向的RMSE分别为0.0232 mm、0.0325 mm和0.0672 mm， 测量误差保持在0.1 mm以内; 在±5°旋转范围， 沿x、y、z轴方向的均方根误差分别为0.0146°、0.0159°和0.0090°， 测量误差保持在0.05°以内. 结果表明， 所研制的测量系统精度满足天线副面并联调整机构的精度需求. 实验结果验证了本文所提方法的可行性和有效性， 为实现并联机构闭环控制提供了有效手段.