日冕中无衰减振荡的研究进展*
高宇航 田晖,2 郭明哲 李波
(1 北京大学地球与空间科学学院 北京 100871)
(2 中国科学院国家天文台 北京 100101)
(3 山东大学空间科学研究院山东省光学天文与日地空间环境重点实验室 威海 264209)
1 引言
日冕中磁雷诺数远大于1, 满足磁冻结条件, 等离子体会被冻结在磁力线上而形成高密度的环状结构, 称为冕环(coronal loop). 冕环是日冕的主要组成部分. 在极紫外(extreme ultraviolet, EUV)波段的图像中, 单个冕环的典型寿命约为几个小时.一般把整个冕环的曲率半径称为大半径, 为几十到几百兆米(Mm); 把冕环横截面的半径称为小半径, 约为1 Mm[1]. 可以看到, 冕环的小半径已经接近目前空间极紫外望远镜的分辨率极限, 比如搭载在太阳动力学天文台(Solar Dynamics Observatory, SDO)上的大气成像仪(Atmospheric Imaging Assembly, AIA)的分辨率约为1 Mm. 一些学者基于数值模型提出(如文献[2-4]), 冕环可能由半径约为几十千米的细丝组成, 目前的仪器水平限制了我们对这些模型的检验. 冕环是日冕中磁流体力学(magnetohydrodynamics, MHD)波的重要载体.目前已经在冕环中发现了多种模式的MHD波, 包括横向扭曲波、腊肠波、纵向的慢波等[1,5-8].
冕环中扭曲波的驻波称为扭曲振荡, 分为衰减振荡和无衰减振荡两种. 衰减振荡从1999年开始在EUV波段中被大量观测到[9-10]. 这种振荡由外部能量释放事件如耀斑、日冕物质抛射(Coronal Mass Ejection, CME)等所激发, 振幅开始为几兆米, 之后随时间推移而很快衰减, 通常短于6个周期; 振幅的衰减可能与共振吸收、开尔文-亥姆霍兹不稳定性(Kelvin-Helmholtz Instability,KHI)等过程有关.关于衰减振荡目前已经积累了大量的研究文献, 可以参考综述文献[1]和[6]的相关部分. 无衰减振荡在2012年由Wang等[11]和Tian等[12]分别通过成像和光谱观测首次发现, 其特征是在振荡的多个周期内具有相近的、无衰减的振幅. 自发现以来, 这种振荡现象已经得到了广泛的关注, 并已证明在冕环中普遍存在.
目前关于无衰减振荡的数值模拟研究主要集中在两个方面, 分别是对其观测性质的解释和对其加热功效的讨论. 此外, 由于无衰减振荡普遍存在,因此具有较高的冕震学(或磁震学)应用潜力, 可以让我们获得冕环及其附近的温度、磁场、密度等信息. 在本综述中, 我们对无衰减振荡的观测性质、理论和数值模拟研究结果以及冕震学应用等方面的进展进行了总结与介绍.
2 观测结果
Wang等[11]利用SDO/AIA和日地关系观测台(Solar TErrestrial RElations Observatory, STEREO)的成像数据, 对2011年3月8日的一次冕环振荡事件进行了分析. 他们通过在冕环顶部取切片(cut)绘制时间-距离图, 首次在冕环中检测到了振幅没有衰减的横向扭曲振荡, 如图1所示. 作者经过分析, 发现这些振荡由CME触发, 持续多个周期,甚至振幅有增长.

图1 左: 在AIA 171 ˚A图像中对振荡冕环做时间-距离图的结果. 右: 从AIA 171 ˚A图像中估计的冕环的位移(黑线)、峰值辐射强度(红线)以及冕环宽度(绿线)的无衰减振荡. 图片来自文献[11].Fig.1 Left: time-distance diagram for an oscillating loop observed in AIA 171 ˚A. Right: decayless oscillations of the loop displacement (black line), peak flux (red line) and loop width (green line) estimated from the AIA 171 ˚A images. This figure is from Ref. [11].
几乎与此同时, Tian等[12]利用日出(Hinode)卫星上极紫外成像光谱仪(EUV Imaging Spectrometer, EIS)的观测数据, 发现了宁静冕环中普遍存在小振幅多普勒频移振荡, 并且明确指出这种振荡在整个观测期间(几个小时内)都无衰减, 振幅为1-2 km·s-1, 周期主要集中在3-6 min, 如图2所示.这些持续存在的小振幅振荡与爆发性事件如耀斑、CME等都没有明显的相关性. 部分振荡事件中同时可探测到辐射强度的小幅振荡, 强度振幅约为2%, 且其与多普勒振荡有π/2的相差. 这种相位差通常被解释为慢驻波信号[13-14], 但是观测到的相速度远远大于典型日冕温度下的声速, 因此慢驻波无法解释这一观测. 结合光谱仪狭缝平行于冕环顶部这一事实, 他们提出, 强度的振荡是因为振荡的冕环周期性地进入和离开狭缝所对准的位置而导致, 即狭缝在不同时刻会对准冕环横截面的不同位置, 而不同位置的密度及辐射强度不一样. 在这种情况下, 他们证明了横向振荡会同慢驻波一样导致π/2的相位差. 此外, 他们还发现一些日冕亮点中也存在无衰减振荡.
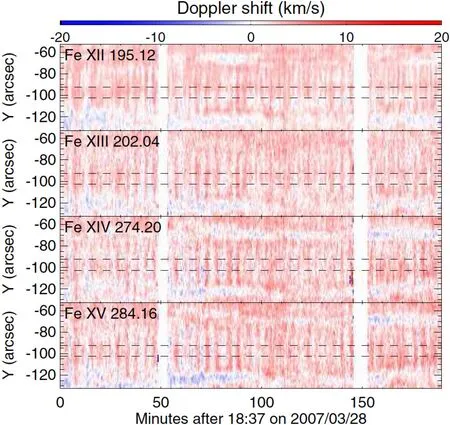
图2 冕环在4条日冕辐射线上的多普勒频移振荡. Y轴大致沿着冕环顶部的方向. 图片来自文献[12].Fig.2 Oscillations of coronal loops seen in Doppler shift of four coronal emission lines. The Y-axis is roughly aligned with the coronal loop. This figure is from Ref. [12].
Nistic`o等[15]对耀斑前后活动区冕环的振荡进行了研究, 观测到衰减振荡和无衰减振荡的共同存在. 衰减振荡出现于耀斑发生之后, 明显为耀斑及其所伴随的CME所激发, 之后振幅以指数形式衰减; 而无衰减振荡则在耀斑发生前后都存在, 说明其触发与耀斑、CME等剧烈能量释放事件无直接关系. 作者将后者命名为无衰减的横向振荡(decayless transverse oscillations), 简称无衰减振荡(decayless oscillations). 这类振荡的观测特征与Tian等[12]发现的持续存在的多普勒频移振荡的特征完全吻合. 尽管是由CME触发的, Wang等[11]从成像数据中观测到的冕环振荡通常也被归类为无衰减振荡.
Anfinogentov等[16]对无衰减振荡进行了统计研究. 他们利用SDO/AIA的171 ˚A波段分析了2013年1月的21个活动区, 对每个活动区观测6 h, 并在活动区的冕环上选取5-10个位置, 引入垂直于冕环的狭缝(slit), 对每个狭缝绘制时间-距离图, 在其中用肉眼检查了振荡是否存在, 测量振荡周期、振幅以及冕环的长度. 他们发现, 低振幅的无衰减振荡在所研究的大部分活动区中都存在; 位移振幅为0.05-0.5 Mm, 平均振幅为0.17 Mm; 振荡周期为1.5-10 min, 平均周期为251 s. 一个重要统计结果是发现了振荡周期与冕环长度的线性相关性, 如图3所示. 对于衰减振荡也发现了类似的相关性[17-18]. 这有力支持了把无衰减振荡视为扭曲驻波的解释. 因为对于扭曲驻波, 周期P与冕环长度L满足P~2L/Ck, 其中Ck表示扭曲波速度(kink speed), 在不同冕环中变化不大, 从而有P ∝L.

图3 振荡周期与冕环长度的关系, 每个点对应统计中的一个振荡事件. 线性拟合用实线表示. 图片来自文献[16].Fig.3 Dependence of the oscillation periods on the loop lengths. Every filled circle corresponds to an oscillation event. The linear fit is shown by the solid line. This figure is from Ref. [16].
Nakariakov等[19]利用文献[16]中给出的数据,绘制了振幅与周期及冕环长度的关系, 发现位移振幅与冕环长度、振荡周期都有正相关关系, 而速度振幅与冕环长度和振荡周期没有明显相关性, 如图4所示.
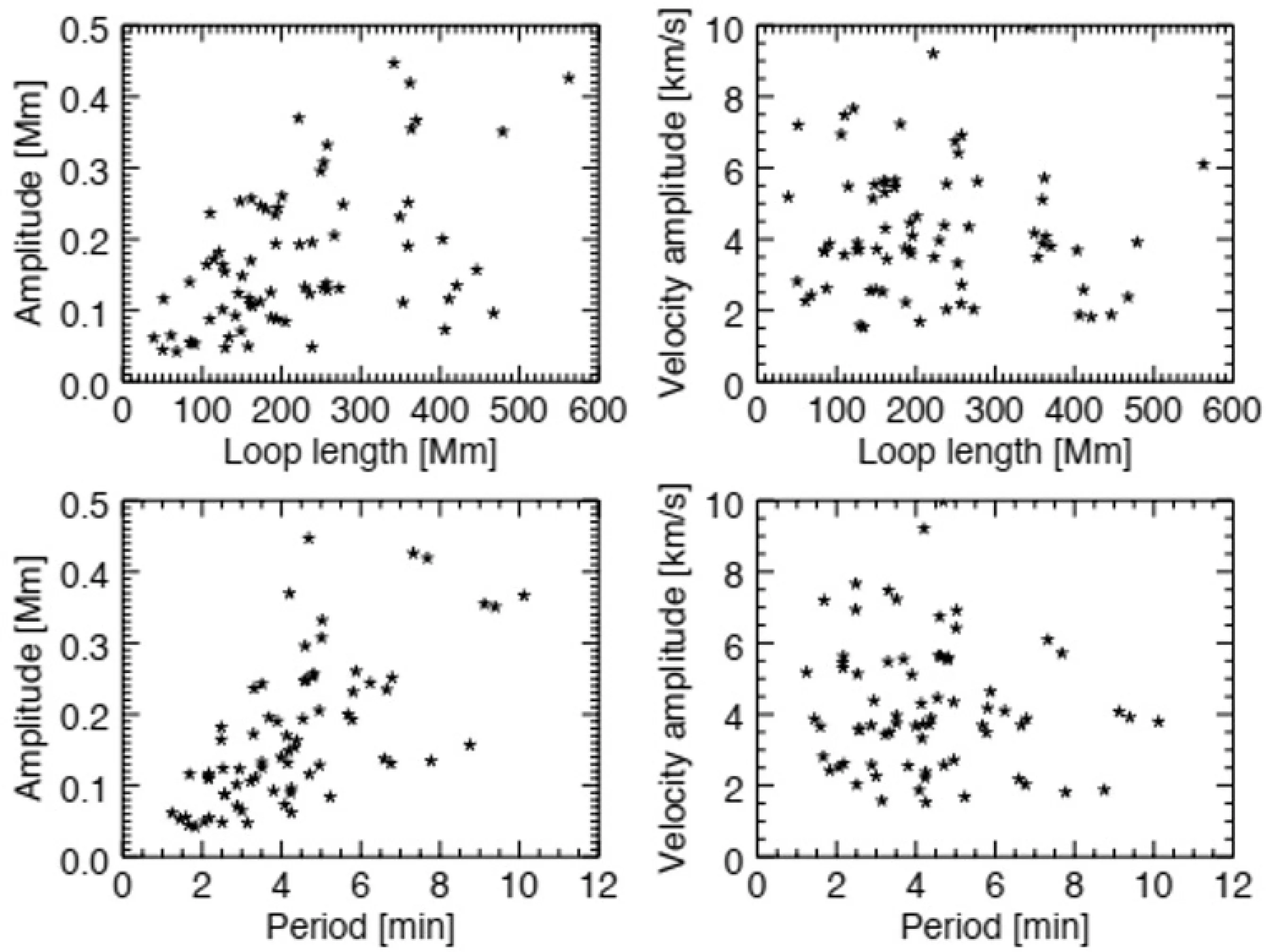
图4 振荡参量与冕环参量之间的关系. 左上: 位移振幅与冕环长度. 右上: 速度振幅与冕环长度. 左下: 位移振幅与振荡周期. 右下: 速度振幅与振荡周期. 图片来自文献[19].Fig.4 Relations of oscillation parameters and oscillating loop parameters. Top left: displacement amplitude vs. loop length. Top right: velocity amplitude vs. loop length. Bottom left: displacement amplitude vs. oscillation period. Bottom right: velocity amplitude vs. oscillation period. This figure is from Ref. [19].
Anfinogentov等[16]还发现了两个值得注意的结论: 其一是同一冕环在不同位置上的振荡是同相位的, 而且振荡只在接近环顶的区域才能被识别,这说明振荡对应于基波. 这进一步印证了他们之前的研究工作[20]. 其二是观测到的冕环都显示在平行方向振荡, 或者说振荡是平行偏振的(horizontally polarized), 即在垂直于冕环所在平面的方向上振荡; 而垂直于太阳表面或沿冕环平面内的横向振荡(即垂直方向或垂直偏振的振荡)则没有被观测到. 冕环横向扭曲振荡的偏振性质最早由Wang等[21]注意到, 他们首先发现了冕环在垂直太阳表面方向上横向振荡的证据, 随后Wang等[22]进一步讨论了在投影效应的干扰下区分平行方向和垂直方向振荡的方法. 尽管Anfinogentov等[16]发现无衰减振荡以平行方向为主, 但是仍有研究发现了垂直于太阳表面的情况[23]. 还有一些更早的工作[24-25]可能也在垂直方向上观测到了衰减不明显的振荡, 但是这些振荡要么与沿着冕环的冷等离子体流动有关, 要么是由耀斑/CME驱动的大振幅振荡, 因而与人们现在对无衰减振荡的定义不同.
近年关于无衰减振荡的一个重要观测结果是Duckenfield等[26]对振荡二次谐波的发现. Duckenfield等[26]首先用多尺度高斯归一化(Multiscale Gaussian Normalization, MGN)方法[27]对AIA的171 ˚A波段中观测到的冕环进行了图像增强(见图5左图), 接着通过一种运动放大算法(motion magnification algorithm)[28]增大了冕环的横向位移振荡信号; 然后他们以冕环顶点为中心, 均匀选取了冕环上的50个狭缝(见图5左图), 分析每个狭缝位置上的横向振荡, 以狭缝编号和周期为参量绘制了无衰减振荡的功率谱, 发现振荡周期在10.3 min和7.4 min处有两个峰值. 前者对应狭缝63 (在冕环顶点附近), 后者对应狭缝43与74 (分别在顶点两侧的冕环两“腿”上), 如图5右图所示.这说明, 无衰减振荡至少具有两个谐波分量, 分别是: 长周期的基波, 在环顶点附近有最大振幅; 短周期的二次谐波, 在冕环两“腿”上各有一个振幅最大处. 进一步的分析还表明, 长周期的谐波在整个冕环长度范围内是同相位的, 短周期的谐波在冕环顶点两侧则是反相位的, 这也符合基波和二次谐波的特征. 对于衰减振荡, 这种高次谐波分量很早就得到了观测[29-31], 并且随即涌现出了大量基于不同次谐波周期比的冕震学工作[32-36]. 相比之下, 由于振幅过小, 对无衰减振荡高次谐波的观测要更为困难(目前还只有图5展示的这一个观测事件); 但是可以预见, 其在冕震学上将有着与衰减振荡同样的应用潜力. 我们将在第4节简述Duckenfield等[26]在该方面作出的一个简单尝试.

图5 左: 冕环在SDO/AIA 171 ˚A波段上的图像, 使用MGN方法对图像进行了增强. 右: 每个狭缝的傅里叶功率谱随周期和狭缝编号的二维分布.图片来自文献[26].Fig.5 Left: SDO/AIA 171 ˚A image of a coronal loop, which has been enhanced using the MGN method. Right: two-dimensional distribution of Fourier spectral power. This figure is from Ref. [26].
最后, 我们将目前冕环无衰减振荡的观测性质总结如下: (1)振幅在观测时间范围内显示出无衰减特性; (2)在冕环中普遍存在, 通常与可见的耀斑或CME等爆发事件没有直接联系(不过, 仍有部分研究关注了耀斑相关的无衰减振荡[37-38]); (3)位移振幅为0.05-0.5 Mm, 速度振幅约为1-2 km·s-1,明显小于衰减振荡(衰减振荡的位移振幅在1-10 Mm, 速度振幅通常在10 km·s-1以上); (4)振荡周期为1.5-10 min, 振荡周期随冕环长度增加而增加; (5)位移振幅与冕环长度及周期显示正相关,速度振幅与冕环长度及周期无相关性; (6)振荡主要在水平方向上(垂直于冕环所在平面), 但也存在垂直于太阳表面方向上振荡的情况; (7)大多数振荡具有准单色性(quasi-monochromatic), 基波振荡最容易观测到, 同时也发现了高次谐波的存在. 其中性质(1)-(3)展示了无衰减振荡与衰减振荡的主要区别, 而性质(4)-(7)则在衰减振荡的观测中也有所反映[17-18].
3 模型与解释
自无衰减振荡被发现以来, 人们就一直对其观测性质及产生机制非常关注. 本节我们将介绍无衰减振荡的理论和数值模拟方面的研究进展.
3.1 主流解释
对无衰减振荡主流的解释是从下述方程出发[15-16, 19, 39]:

其中ξ表示振荡冕环的位移;γ表示振荡的阻尼, 通常由共振吸收等机制[40-41]提供; Ωk表示扭曲振荡的固有频率;f(t)表示驱动项, 根据不同的驱动机制将选为不同的形式. 根据f(t)的不同, 可以把这种主流解释的模型分为3种, 分别是简谐驱动模型、自振荡(self-oscillatory)模型和随机驱动模型.
3.1.1 简谐驱动模型
简谐驱动模型中,f(t)取为简谐形式. Nistic`o等[15]把无衰减振荡和衰减振荡放在一起建模, 把驱动力取为:

其中a0e-iωt表示驱动无衰减振荡的简谐作用,a0表示简谐作用的幅度,ω表示简谐作用的频率;a1δ(t-t0)则表示驱动衰减振荡的能量爆发事件,a1表示爆发事件的强度,t0为爆发事件发生的时间. 他们利用这一模型绘制出的冕环顶点位移随时间变化的曲线与观测较为吻合. 但是, 这种模型存在着不少问题. 比如, 图3反映了振荡周期与由基波主导的冕环固有频率相一致, 但是Ballai等[39]认为简谐驱动下的振荡周期将与驱动力的周期相对应, 而事实上后者不可能总是接近冕环的固有频率, 所以图3的结果实际上不支持这种模型. 类似的,Nakariakov等[19]也指出,简谐驱动模型下,振荡振幅与周期的关系应该有一个明显的峰值, 峰值对应于和简谐驱动力频率ω相等的共振频率. 然而从图4中可以看到, 位移和速度振幅与周期的关系图中都不存在这种峰值. 此外, 一些观点认为, 简谐驱动力可以与太阳黑子的3-5 min振荡联系起来; 但是统计研究表明, 无衰减振荡与活动区中太阳黑子的存在与否没有明显相关性[16].
尽管简谐驱动模型存在上述困难, 但是其优点在于模型比较简单, 也可以比较好地再现振荡的无衰减特性. 所以, 在对无衰减振荡的三维MHD模拟工作中, 这种模型还是得到了比较广泛的应用[42-45]; 这些模拟工作的重心往往在于KHI的发展与冕环的加热效率等方面, 并未特别关注模型能否很好地再现所有的观测特征. 在这些模型中, 往往于冕环足点处引入一个简谐振荡的速度边界条件, 即

其中v0为常量. 这本质上还是提供一个简谐形式的驱动力.
一般来说, 简谐驱动模型中在冕环足点引入的简谐力都是水平方向的, 即平行于太阳表面. 不过也有一些理论和数值模型[46-47]尝试采用垂直方向简谐振荡的驱动力来解释无衰减振荡.
3.1.2 自振荡模型
第2种模型称为自振荡模型, 由Nakariakov等[19]提出. 可以用传送带-弹簧模型来对这种模型进行说明, 见图6. 图中重物的振荡对应于冕环的扭曲振荡, 弹簧和传送带都会给重物提供阻尼: 弹簧的阻尼对应的是扭曲振荡自身由于共振吸收等效应导致的阻尼; 传送带提供的阻尼对应于驱动项f(t), 与相对速度有关, 可以表示为F(v0-dξ/dt).从而我们可以把(1)式写为:
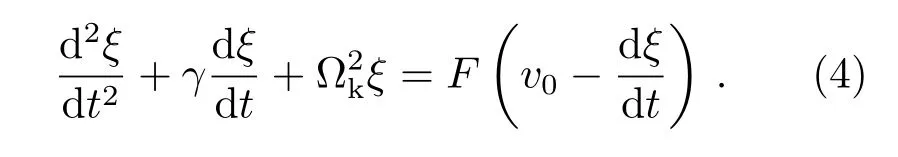

图6 自振荡模型的示意图, 图片来自文献[19].Fig.6 Sketch of the self-oscillatory model. This figure is from Ref. [19].
对F进行泰勒展开, 即得到瑞利振子方程(Rayleigh Oscillator Equation)


在这种模型中, 无衰减振荡由有效负阻尼引起的自振荡过程导致. 能量的来源是一种外部的准稳定流, 在传送带-弹簧模型中, 对应的是具有稳定速度v0的传送带; 在实际情形中, 这种准稳定流可能由冕环足点处的超米粒运动提供(如图6所示),也可能由CME产生. Wang等[11]在振荡冕环足点附近发现的暗化区域暗示了这种由CME爆发诱发的强外流(参见文献[50-51])的存在, 这种流动引起的自振荡过程或许可以解释他们观测到的无衰减振荡(如图1所示).
Nakariakov等[19]提出这一机制时, 所给出的只是一个仅与时间有关的半经验模型, 也无法解释之后观测发现的高次谐波. Karampelas等[52]基于这种模型进行了三维MHD模拟, 并且考虑了垂直方向上的重力分层效应. 他们在冕环足点附近引入了一个缓慢变化的准稳定流, 以此模拟光球上的超米粒运动, 得到了图7所示的结果. 在左图中, 可以看到在约38 min时, 有一个周期P~161 s的振荡开始产生. 右边的功率谱密度(Power Spectral Density,PSD)图中, 可以在频率(纵坐标)为1P-1处看到一个明显的峰值, 对应的是扭曲模的基波. 除了主要峰值之外, 还可以在其上方看到一个较弱的额外峰值, 对应于二次谐波. 二次谐波与基波的频率比大约为1.7-1.8, 与文献[26]中约1.4的观测结果相近.研究还表明, 自振荡的激发需要时间尺度在1 h量级的准稳定流. 需要指出, 这一模拟工作仍然只是从概念上证明了自振荡模型在三维MHD模拟中可以产生无衰减振荡以及高次谐波. 模拟的结果与观测不能很好地吻合(见图7左图), 得到振幅也只是典型观测值(约0.1 Mm)的1/10.
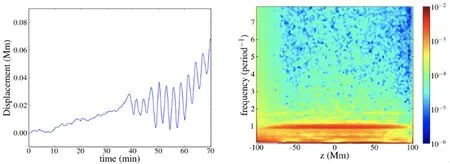
图7 左: 模拟中由稳定背景流激发的冕环顶点的横向位移. 右: 横向位移的功率谱密度随z轴位置和频率的分布. 模拟中冕环被建模为磁通量管, 冕环的两足点分别位于z = ±100 Mm处, 冕环顶点对应z = 0. 图片来自文献[52].Fig.7 Left: transverse displacement of the loop apex excited by a steady background flow in the simulation. Right: power spectral density of the transverse displacement as a function of z position and frequency. The loop is modeled as a magnetic flux tube in the simulation. The loop footpoints are placed at positions z = ±100 Mm, while z = 0 is the location of the loop apex.This figure is from Ref. [52].
Karampelas等[53]于2021年又进一步利用三维MHD模拟研究了日冕中涡旋脱落(vortex shedding)过程[54-56]导致无衰减振荡的机制. 这种机制认为, 来自日冕中强背景流的涡旋脱落会对冕环产生周期性的“推动”作用, 进而维持冕环的振荡.由于被激发的振荡频率同时取决于强背景流的速度和冕环的性质, 而且背景流是恒定的而非周期性的, 所以这种机制也被视为自振荡模型. 在他们的模拟结果中, 无衰减振荡得到了激发, 并且也可以看到高次谐波的存在. 不过, 此工作仍然只是提供了一个通过涡旋脱落维持无衰减振荡的概念性证明, 要与观测进行比较还需要在模型中进一步考虑重力分层效应、实际的背景流剖面等因素.
3.1.3 随机驱动模型
在随机驱动模型中, (1)式中的f(t)将取为随机函数R(t). 这种机制由Anfinogentov等[16]提出, 并且把随机驱动力与冕环足点处的米粒随机运动联系了起来. Nakariakov等[19]也讨论了这种模型, 但是认为此情况下振荡相位和振幅均呈现间歇性的不规则变化, 与大部分观测情况不符. 不过Nistic`o等[57]在观测中有发现过这种不规则的振荡特征.
Afanasyev等[58]建立了一种新的随机驱动模型, 并且在解释无衰减振荡观测性质方面取得了不错的结果. 在他们的模型中, 考虑了垂直方向的重力分层, 扭曲波速度会沿冕环变化. 在冕环的两个足点处, 他们输入了色噪声(coloured noise)信号,对应幂律谱指数为1.66的随机足点运动. 这种幂律谱被磁亮点动力学性质的观测[59-60]所支持. 图8展示了足点处的输入信号以及模拟结果, 可以看到作为谐振器(resonator)的冕环中振荡本征模的激发, 而且二次谐波与基波的频率比值约为1.7, 与文献[26]中得到的观测值1.4相近. 图8的右下图展示了模拟得到的冕环顶点处的位移情况, 振荡的振幅在多个周期内表现出无衰减的特性; 虽然从中仍然可以看出一些小尺度的间歇性特征, 但是研究者认为在AIA的分辨率下这些特征很可能是无法分辨的, 因此结果可以与AIA的极紫外观测相吻合.
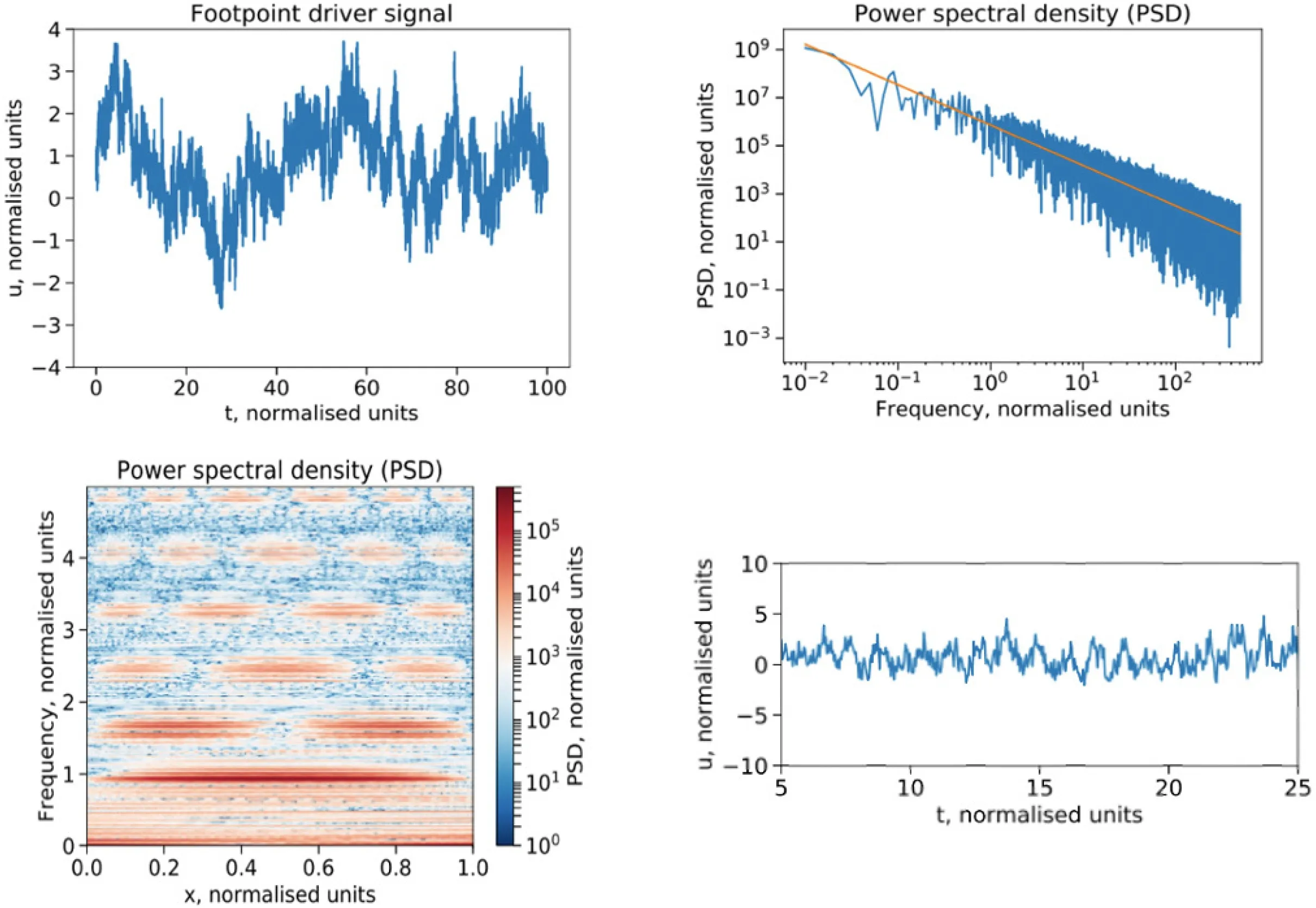
图8 左上: 作为输入信号的冕环足点处的位移. 右上: 冕环足点位移的功率谱密度, 橙色线显示了指数为1.66的功率谱幂律衰减. 左下: 冕环位移的功率谱密度. 右下: 冕环顶点的位移. 图中横坐标t表示模拟开始后的时间, x表示沿冕环的距离, 均以归一化单位表示. 图片来自文献[58].Fig.8 Top left: loop footpoint displacement as an input signal. Top right: power spectral density of the loop footpoint displacement. The orange line shows the spectral power-law fall-offwith an index of 1.66. Bottom left: power spectral density of displacements of the loop. Bottom right: displacement of the loop apex. In the figure, t is the time after the start of the simulation, while x is the distance along the loop. They are both shown in the normalised units. This figure is from Ref. [58].
Afanasyev等[58]给出的随机驱动模型可以再现无衰减振荡的多个观测性质. 因为激发的振荡周期由冕环长度和扭曲波速度决定, 所以周期与冕环长度之间自然应当具有相关性. 模拟中速度振幅完全由足点处的随机噪声导致, 所以速度振幅与冕环长度及周期无关. 模拟得到的PSD分布(图8左下)可以说明振荡的准单色性、高次谐波的出现以及非整数的谐波频率比值. 此外, 在自振荡模型中, 输入能量的外部流动(如超米粒运动)其特征时间尺度远远长于无衰减振荡的观测周期; 而此模型中足点随机运动的特征时间尺度(与米粒运动有关)则是与观测周期相近的. Afanasyev等[58]提出的随机驱动模型具有相当的潜力, 但还有待于在三维MHD模拟中加以进一步的检验. 最近, Ruderman等[61]在Afanasyev等[58]工作的基础上, 把冕环建模为具有一个过渡层(transitional layer)的磁通量管,解析推导了稳定随机函数驱动下的谐波控制方程与功率谱, 讨论了谐波频率比、半高峰宽和过渡层厚度之间的关系.
1.4 统计公式 各处理均在培养45 d后统计结果,记录诱导率、出芽情况、芽增殖倍数及生长状况。诱导率=[形成愈伤组织的茎段数/(接种总的茎段数-污染数)]×100%;芽增殖倍数=(增殖后芽总数/增殖前芽个数)×100%。
3.2 KHI涡旋模型
Antolin等[62]把无衰减振荡建模为由共振吸收过程增强的KHI涡旋, 或称为横波导致的开尔文-亥姆霍兹滚流(Transverse Wave Induced Kelvin-Helmholtz rolls, TWIKH rolls). 他们的工作把三维MHD模拟与正演建模(forward modeling)结合起来, 可以在当前空间分辨率下得到与观测类似的小振幅振荡. 这种振荡是KHI产生的周期性增亮与KHI涡旋的相关运动共同导致的结果. KHI涡旋由与扭曲振荡共振耦合的角向Alfv´en波产生, 而这种Alfv´en波相对于扭曲模具有较低的阻尼, 从而使振荡在一定时间内显现出无衰减特性. 这种模型得到的位移振幅及周期与观测一致, 也可以解释观测发现的辐射强度的周期性变化[12]. 但是, 模型中没有额外的能量输入, 本质上是认为KHI涡旋可以延长振荡的阻尼时间, 所以振荡最终还是会衰减, 这与观测不符(例如文献[11]发现, 振荡振幅甚至可能在一些时间间隔内增大).
如果在这一模型的基础上引入外部能量源(即驱动机制), 就有希望解决上面的问题. Guo等[44]考虑了3种不同驱动机制的KHI涡旋模型,分别是: (1)扭曲模驱动: 对应冕环足点在特定方向上的简谐运动, 即主流解释中的简谐驱动模型; (2)由Alfv´en模驱动: 对应冕环足点的涡旋运动; (3)混合驱动: 即把前两种足点运动模式混合起来, 对应的是随机驱动模型. 模拟发现, 扭曲模驱动和混合驱动这两种机制都可以再现无衰减振荡的观测结果; 而在混合驱动下, 可以诱发更多的湍流结构, 带来更强的加热效应. 图9展示了混合驱动的情况: 左边的强度图中可以看到与观测(参见图1左图)类似的无衰减振荡图样; 右边的多普勒速度图中可以看到明显的湍流, 分辨率降低之后的图像(右下)则可以与图2给出的观测结果进行比较.

图9 混合驱动情况下的171 ˚A波段上的冕环顶部的正演结果. 左: 归一化辐射强度的时间-距离图. 右: 多普勒速度的时间-距离图. 上图为完整数值分辨率下的图像, 下图为把分辨率降低到与AIA相近后的图像. 图片来自文献[44].Fig.9 Forward-modeling results for the mixed driver in the 171 ˚A line at the loop apex. Left: time-distance maps of the normalised intensities. Right: time-distance maps of the Doppler velocity. The upper panels are obtained with the full numerical resolution and the lower panels are obtained with a degraded resolution comparable to AIA. This figure is from Ref. [44].
目前对无衰减振荡的三维MHD模拟工作多数都是基于简谐驱动和KHI涡旋模型. 这些工作通常更关注KHI的发展、冕环对足点驱动力的响应、振荡对日冕加热的贡献等问题. Karampelas等[43]研究了无衰减振荡的振幅与冕环足点处简谐驱动力振荡强度的关系, 发现两者之间相关性较弱, 也难以建立输入能量通量与位移振幅之间关系. Howson等[63]研究了在振荡的冕环中, 电阻率和粘性对KHI产生和发展的影响, 发现更大的电阻率和粘性会抑制KHI的发展. Afanasyev等[64]研究了振荡冕环对其外部激发源的共振响应、考虑重力分层后不同高度上的KHI发展, 进而讨论了振荡引起的等离子体加热的空间分布. Shi等[45]首次在模拟中考虑了辐射损失效应, 发现无衰减振荡的能量耗散很有希望平衡冕环的辐射损失, 从而为解决日冕加热问题开拓了一条新途经.
3.3 垂直于太阳表面的无衰减振荡的解释模型
文献[16]指出, 冕环无衰减振荡主要是水平方向或水平偏振的. 由于人们也发现了垂直于太阳表面振荡的证据[23-25], 所以也提出一些模型以解释这种振荡模式.
Kohutova等[65]利用2.5维MHD模拟, 发现在冕环顶部的冷凝等离子体在重力作用下下降, 可以激发垂直方向的无衰减振荡, 即持续的冕雨可以成为冕环无衰减振荡的激发机制. 这种机制只能激发属于基波的垂直振荡, 振荡周期会随冕环的质量变化而变化.
Kohutova等[66]随后又在Ofman等[67]的启发下, 提出了通过引入虹吸流来解释这种振荡的模型. 该模型认为冕环一个足点上的气压增强(例如由局部加热导致)会触发沿冕环运动的高速等离子体流, 即虹吸流; 离心力的作用会导致冕环产生向外的位移, 随后在洛伦兹力的回复作用下冕环又会被拉回, 这样就激发了对应基波的扭曲振荡. 模拟结果表明, 实际速度小于100 km·s-1(这也是观测中发现的冕环中等离子体流的典型速度[68-69])的虹吸流就足以激发具有可观测振幅(约1 Mm)的振荡.
垂直于太阳表面方向上的无衰减振荡在观测和模拟上受到的关注都是比较少的. 而且在多数无衰减振荡的理论和模拟研究中, 都没有对振荡的偏振性质进行任何讨论[19,52-53,58]. 事实上, 文献[16]指出, 主流解释给出的(1)式将以相同的效率产生水平和垂直于太阳表面方向上的振荡, 不能解释观测中水平方向为主的情况; 无衰减振荡对于水平方向的偏好, 也可能暗示着传统的把冕环建模为等离子体圆柱的模型存在一些问题, 例如Hindman等[70]就认为他们提出的基于磁拱的新模型(见3.4节)能更好地解释振荡偏振方向的问题. 未来有必要在观测上对垂直于太阳表面的无衰减振荡进行进一步研究, 同时在数值模拟中寻求对无衰减振荡偏振性质更好的解释.
3.4 非圆柱型冕环模型
冕环通常在模拟中被建模为单个或多个成束的等离子体圆柱. 近年一些研究工作表明, 这样的建模可能存在很多问题, 不能很好地与实际情况对应[3,43,71]. 因此, 有人提出了一些非圆柱型的冕环模型来解释无衰减振荡. Hindman等[70]基于磁拱组成的二维波导建立了一个分解析模型, 模型中也可以再现衰减振荡和无衰减振荡, 前者由脉冲式的能量源产生, 后者则由连续、随机的能量源维持, 本质上仍可归为随机驱动. 由于在此模型中, 波导(或冕环)被建模为相邻的磁拱, 所以研究者认为可以用磁拱之间的相互作用来解释观测中水平方向振荡为主的情况, 这一模型目前还在不断发展之中[72-73].
Kohutova等[74]使用辐射MHD代码Bifrost[75],在模拟中考虑了真实的磁场位形及演化. 进行正演模拟后, 他们在模拟区域内发现了磁力线所对应的类似冕环的结构, 并且在冕环中发现了衰减振荡和无衰减振荡的存在. 他们检查了冕环上横向速度分量在时间和空间上的变化, 发现在模拟开始后500 s时, 某个脉冲式的能量释放过程激发了一个衰减振荡; 而在整个模拟时间范围内, 一直存在一个持续的、振幅在5 km·s-1左右的无衰减振荡. 同时, 纵向速度分量随时间的演化图中也可以看到振荡的存在, 对应于纵向的慢波. 通过追踪冕环足点处的运动特征, 研究者认为这里的无衰减振荡与足点处的简谐运动无关, 相当于排除了简谐驱动机制. 此外, 模拟区域中流动较为动态, 在分钟量级, 所以也无法产生自振荡机制所要求的小时量级的准稳定流[52]. 不过, 研究者并没有明确指出具体是什么机制驱动了无衰减的横向振荡, 模型中也没有引入任何初始扰动. 这一模型的问题在于模拟的磁结构和密度结构与真实日冕存在差异, 比如正演得到的图像中冕环显得较为弥散, 与观测有较大不同. 不过, 这种模型可以成功再现多种冕环振荡模式, 包括横向的衰减振荡和无衰减振荡以及纵向的慢波;在其中一些冕环(磁力线)上还发现了横向振荡二次谐波的存在. 这些都使得该模型具有进一步发展的潜力.
4 无衰减振荡的冕震学应用
由于冕环的无衰减振荡在日冕中普遍存在, 所以一个很自然的想法就是将其应用于冕震学. Tian等[12]指出, 利用这种普遍振荡现象的观测特征有可能对冕环的磁场进行诊断. Anfinogentov等[76]在无衰减振荡的冕震学应用上走出了很大的一步, 获得了对冕环内Alfv´en速度的有效估计. 他们应用运动放大算法研究了2014年7月10日活动区12107的8个冕环(图10展示了所研究的活动区, 左图用彩色虚线标出了这8个冕环), 测得了冕环的长度L(通过假设冕环为半圆形)和P, 从而估算出Ck= 2L/P.之后根据冕环内外的辐射强度的比值对密度比η(冕环外部密度与冕环内部密度的比值)进行了估计, 估计时假设内外等离子体是等温的. 由密度比和Ck, 即可计算冕环内和冕环外的Alfv´en速度, 分别为

其中下标0和e分别表示冕环内和冕环外. 需要注意的是, (7)式的导出应满足冕环内外磁场相等的假设. 用上述方法得到的结果显示, 虽然密度比和外部Alfv´en速度的估计有很大的不确定性, 但是对内部Alfv´en速度的估计是比较可靠的, 不确定度在15%-20%. 估测的结果展示在图10的右图中. 由于研究忽略了重力分层效应, 所以得到的Alfv´en速度值为沿冕环的平均值.
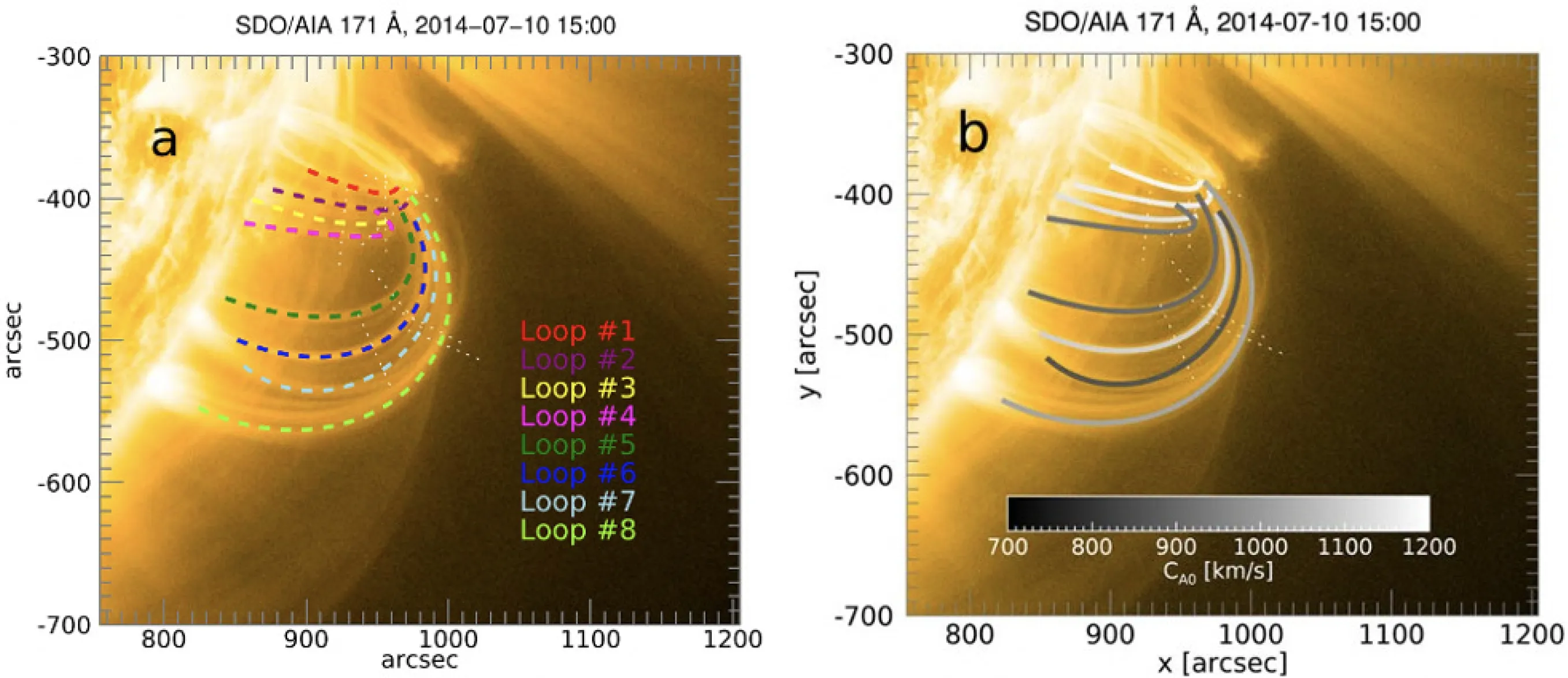
图10 左: SDO/AIA在171 ˚A观测到的极紫外图像. 用于分析的冕环用彩色虚线标记. 右: 冕环内Alfv´en速度的估计结果. 图片来自文献[76].Fig.10 Left: EUV image observed by SDO/AIA at 171 ˚A. Coronal loops for the analysis are overplotted with the colored dashed lines. Right: estimation results of the internal Alfv´en speed. This figure is from Ref. [76].
Alfv´en速度满足

其中B为磁场,μ为磁导率,ρ0为冕环内密度. 如果使用一些独立的方法-例如正演模拟方法[77]或微分发射度(Differential Emission Measure, DEM)方法[78]-得到冕环内部的密度ρ0, 就可以计算出冕环的磁场. 这或许是未来可以进行的工作. 此外, 通过考虑密度分层效应或者振荡的高次谐波, 我们或许能进一步得到冕环内Alfv´en速度的空间分布; 通过使用某些方法对冕环内外密度比进行更精确的测量(例如文献[79-80]), 我们也有机会得到对冕环周围等离子体密度的更可靠估计.
Antolin等[62]从理论上讨论了一种进行密度诊断的冕震学方法. 就他们所讨论的模型而言, 谱线193 ˚A和171 ˚A分别对应冕环的边界层(boundary layer)与核心. 由于相混合效应, 前者观测到的无衰减振荡应当有更短的周期. 理论计算可以给出不同谱线观测得到的振荡周期之比与冕环边界层及内外密度的关系, 由此就能估算冕环的边界层密度和内外密度比等信息. 不过以上讨论目前仍限于理论, 不同波段下无衰减振荡的周期差异似乎也并不普遍, 比如图2给出的观测结果就没有显示明显的周期差异.
Duckenfield等[26]借鉴基于衰减振荡的冕震学方法, 利用观测中得到的基波与二次谐波的周期比(频率比), 给出了一个对密度标高的简单估计. 他们的估计基于[32-33]

其中P1和P2分别为基波和二次谐波的周期,H为密度标高. 观测得到的周期比P1/P2≈0.69±0.16, 再取L ≈292 Mm, 从而可以得到H大约为7-45 Mm,与之前的一些研究给出的结果[34,81]较为符合.
衰减振荡由于发现更早、研究更充分, 目前已经积累了大量冕震学应用方面的研究成果[1,35]. 其中许多成果或许可以移植到无衰减振荡上, 帮助我们诊断日冕中的物理参数.
5 总结与展望
冕环的无衰减振荡自2012年被发现以来, 在观测和数值模拟上都得到了比较丰富的研究, 其在冕震学上的应用也显示出了相当的潜力.
对无衰减振荡的观测研究主要使用SDO/AIA的171 ˚A波段和绘制时间-距离图的方法. 统计结果显示这种振荡普遍存在于冕环中, 是一种准单色的扭曲驻波. 相对于衰减振荡, 无衰减振荡具有较小的振幅, 接近目前可用仪器的分辨率极限, 为更精细的观测研究带来了困难. 新开发的运动放大算法[26,28,76]可以在一定程度上放大振荡的信号, 对无衰减振荡二次谐波的发现就要归功于这一方法.统计研究中发现了振荡参数之间的经验关系[16,19],对振荡模式的确认以及模拟工作的开展都有重要意义. 观测还发现无衰减振荡在偏振性质上与衰减振荡类似, 均是以水平方向上的振荡为主.
如何构建模型对无衰减振荡观测性质进行解释是日冕MHD波动研究的一个重要课题. 主流的解释是把冕环建模为等离子体圆柱, 通过在波动方程中加上驱动项f(t)来对抗共振吸收等阻尼机制. 根据对f(t)的不同选择, 又可以把主流解释分为简谐驱动、自振荡和随机驱动3种模型; 目前来看, 似乎最后一种模型在对观测性质的解释上最为成功. 我们注意到, 各种解释模型往往都经历了从空间0维(即只依赖于时间)到空间一维(考虑密度分层效应)再到成熟的三维MHD模拟的过程; 而三维MHD模拟中, 无衰减振荡又往往同共振吸收相关的KHI涡旋或TWIKH滚流密切相关[44,62].此外,也有很多研究者利用三维MHD模拟研究了无衰减振荡冕环中KHI的发展以及振荡对日冕等离子体的加热效应[42-45,63-64]. 还有一些研究探索了不把冕环建模为等离子圆柱的新模型[70,72-74], 但是影响仍相对较小.
在无衰减振荡的冕震学应用上, 多数研究还只是从理论和模拟的角度上探讨了一些可能的方法[26,58,61-62]. 目前这方面最值得注意的成果是对冕环内部Alfv´en速度的估计[76]. 虽然这一诊断方法还有待进一步发展, 但是它还是成功地表明无衰减振荡在冕环物理参量诊断上具有强大的潜力.
无衰减振荡有着两个重要的研究意义: 一是其作为长时间稳定存在于日冕中的横向振荡, 可能在日冕的能量传输和转换过程中有重要作用, 因此与日冕加热有着直接的相关性; 二是这种振荡普遍存在的特性, 使之可以成为冕震学的有效工具, 帮助我们对冕环的磁场等物理参数进行诊断.
目前我们对无衰减振荡的研究仍存在很多欠缺, 特别是虽然提出了很多种解释模型, 但是这些模型通常只偏重观测事实的不同侧面. 把模型同观测更好地结合起来应当是未来值得重点关注的工作. 此外, 在观测上, 无衰减振荡的高次谐波成分与偏振特征都有待于更充分的研究, 同时也有必要对振荡进行更多类似文献[12]的光谱学观测; 在模拟上, 一些解释机制仍有待于发展为成熟的三维MHD模型, 无衰减振荡的偏振特性模拟也应当受到进一步的关注. 最后, 与无衰减振荡的冕震学应用相关的研究可以说也只是刚刚开始, 同样有着广阔的发展前景. 随着太阳轨道器(Solar Orbiter)、丹尼尔·井上太阳望远镜(Daniel Ken Inouye Solar Telescope, DKIST)等新太阳观测设备的投入使用,我们可以预期在不久的将来进一步加深对无衰减振荡的认识. 比如, 太阳轨道器卫星上搭载的极紫外成像仪(Extreme Ultraviolet Imager, EUI)[82]可以对日冕进行前所未有的高分辨率成像观测, 利用其数据将可以对冕环精细结构和日冕亮点的无衰减振荡特征进行研究. DKIST可以通过偏振测量来诊断日冕磁场, 将其与本文提到的冕震学诊断结果进行结合, 我们将能对日冕磁场有更全面的理解.新望远镜将带来海量观测数据, 我们也可以通过日冕图像自动识别方法来搜索并分析冕环无振荡衰减现象[83-84].

