基于固定频率二阶广义积分器的改进型ip-iq谐波检测算法
张爽 ,刘海涛,牛健,赫嘉楠,王云鹏,李国胜
(1.宁夏电力有限公司电力科学研究院,宁夏 银川 750000;2.山东容弗新信息科技有限公司,山东 济南 250000;3.输配电装备及系统安全与新技术国家重点实验室(重庆大学),重庆 400044)
随着我国电力行业的快速发展,以风电和光伏为代表的大规模新能源并入电网,以及大量的非线性大容量电力电子设备的投入使用,给常规电力系统稳定性、可靠性等带来严重的挑战,其中给电能质量领域带来了丰富的谐波干扰就是其中之一[1]。对谐波准确检测是一切谐波研究工作的前提[2],因此,对谐波检测算法进行研究具有重要意义。
目前,常用的谐波检测方法主要有:基于快速傅里叶变换和小波变换的谐波检测算法、基于神经网络的智能谐波检测算法、基于希尔伯特黄变换的谐波检测算法、基于瞬时无功理论的谐波检测算法等。快速傅里叶变换只能检测稳态谐波,无法对暂态谐波进行检测,另外存在频谱泄漏等问题[3-4];小波变换虽然能够对谐波进行时频分析,但实现较为复杂[5];神经网络算法虽然检测精度高,但大多依靠经验对网络进行训练[6];希尔伯特黄变换能够对暂态谐波进行分析,但也存在模态混叠和端点效应等缺陷[7];基于瞬时无功理论的谐波检测算法在实际使用中实现简单,能够对谐波实时检测,目前在电力系统领域中广泛应用[8]。传统基于瞬时无功的谐波检测算法受锁相环(phase-locked loop,PLL)提供的频率精度和低通滤波器(low-pass filter,LPF)滤波效果的影响[9]。文献[10]提出一种可以检测出三相电路中各个频段的正序和负序谐波的ip-iq谐波检测算法,可以弥补传统ip-iq法的不足。文献[11]提出了一种无锁相环的ip-iq谐波检测方法,但添加了锁频环结构,并未从根本上实现无锁相锁频结构。文献[12]提出一种基于改进二阶广义积分器(second order generalized integrator,SOGI)的ip-iq谐波检测算法,利用SOGI的滤波特性为ip-iq提供更准确的电压频率,但SOGI在电网频率突变时输出正交信号不等幅,容易使锁相过程出现偏差。
本文利用改进型固定频率的二阶广义积分器(improved frequency-fixed second order generalized integrator,IFFSOGI)与传统ip-iq谐波检测算法相组合,提出了一种基于固定频率二阶广义积分器的改进型ip-iq谐波检测算法。IFFSOGI不仅具有良好的带通滤波器特性,还能够克服传统二阶广义积分器输出正交信号不等幅问题,该算法利用IFFSOGI滤除电网中直流成分和多次谐波,并利用IFFSOGI构成的锁相环准确锁定电网频率,从而ip-iq检测到更准确的谐波信息。最后,仿真算例验证了所提谐波检测算法的有效性。
1 基于改进型固定频率二阶广义积分器的锁相环
1.1 二阶广义积分器
图1为二阶广义积分器(SOGI)的基本结构原理,Ug为电网电压,ω′为估计电网角频率,k为控制增益,Uα和Uβ为一组正交信号。由图1可知,估计的电网频率ω′实时反馈给SOGI,从而实现频率自适应。

图1 二阶广义积分器结构图Fig.1 Structure diagram of SOGI


1.2 固定频率二阶广义积分器
为克服SOGI的不足,采用的固定频率的二阶广义积分器(frequency-fixed second order generalized integrator,FFSOGI)结构图如图2所示。在图2中,ω0为谐振角频率,一般取ω0=100π,从而实现FFSOGI与锁相环解耦。

图2 固定频率二阶广义积分器结构图Fig.2 Structure diagram of FFSOGI
FFSOGI的传递函数为
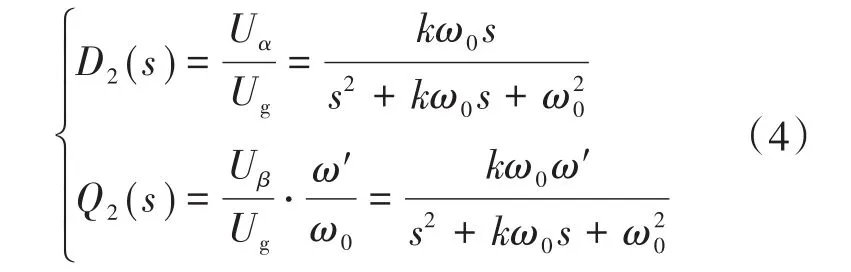
由式(2)可得FFSOGI输出正交信号为

由式(5)可知,稳态时,ω′≈ω,FFSOGI输出正交信号幅值始终相等,从而保证锁相环锁相正确。
1.3 改进型固定频率二阶广义积分器
FFSOGI是在传统SOGI模块基础上改进而来,所以FFSOGI不可避免只能滤除信号中高次谐波,仍受到电网直流成分和低次谐波的影响,因此提出一种改进型固定频率二阶广义积分器(improved frequency-fixed second order generalized integrator,IFFSOGI),其结构如图3所示。

图3 改进型固定频率二阶广义积分器结构图Fig.3 Structure diagram of IFFSOGI
由图3可知,改进型FFSOGI在SOGI模块内部添加了一个控制回路,该控制回路由控制参数k1来调节,该回路与SOGI模块配合工作。
IFFSOGI的传递函数为

式(6)对应的幅频特性如图4、图5所示
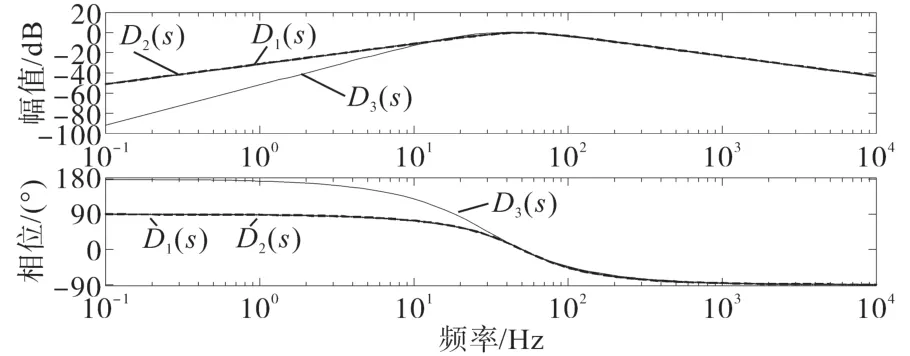
图4 D(s)幅频特性曲线Fig.4 Amplitude frequency characteristic curves of D(s)
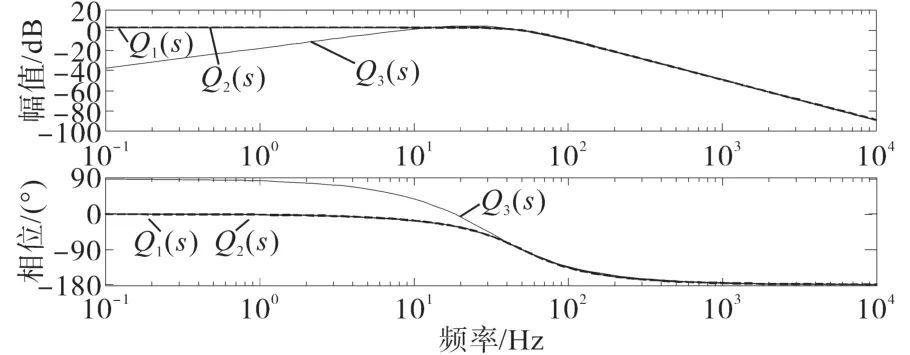
图5 Q(s)幅频特性曲线Fig.5 Amplitude frequency characteristic curves of Q(s)
由图4可知,D1(s),D2(s)和D3(s)均表现出带通滤波特性,D1(s)和D2(s)幅频特性曲线重合,三者都能滤除信号中的直流成分和各次谐波,其中D3(s)在低频段负数增益大于D1(s)和D2(s),说明滤除直流成分和低次谐波能力优于其他两种传递函数。在图5中,Q1(s)和Q2(s)仅表现出低通滤波特性,无法将直流成分和低次谐波进行滤除,Q(3s)表现出带通滤波特性,不仅有Q(1s)和Q(2s)相同的滤除高次谐波能力,也具有良好地滤除直流成分和低次谐波能力,验证了IFFSOGI良好的带通滤波特性。
根据文献[12]可知,在传统SOGI中,参数k一般取。借鉴文献[13]的思想,可根据传递函数幅频特性曲线确定k1的值,在谐振角频率ω0=100π处作出不同k1时D3(s)的幅频特性曲线,如图6所示。

图6 D3(s)幅频特性曲线Fig.6Amplitude frequency characteristic curves of D3(s)
由图6可知,k1影响D3(s)低频段负数增益,其值越大,负数增益越大,直流抑制能力越强,但也在工频处产生正数增益,影响基波幅值。因此k1值需要折中考虑,本文取k1=0.22。
1.4 基于改进型固定频率二阶广义积分器的锁相环
基于IFFSOGI的锁相环结构如图7所示。与传统锁相环相比,IFFSOGI-PLL利用IFFSOGI对电压信号进行滤波处理,滤除信号中的直流成分和各次谐波,为基于同步坐标系的锁相环(synchronous reference frame-phase locked loop,SRFPLL)提供准确的正交信号,最后利用SRF-PLL进行准确锁相。

图7 IFFSOGI-PLL结构图Fig.7 Structure diagram of IFFSOGI-PLL
2 基于IFFSOGI的ip-iq谐波检测算法
2.1 传统ip-iq谐波检测算法
传统ip-iq谐波检测算法采用SRF-PLL对电网电压进行锁相,为其提供角频率,同时利用LPF滤除信号中的高次谐波,最后利用电网三相电流与基本电流做差得到电网谐波电流。其结构如图8所示。

图8 传统ip-iq谐波检测算法结构图Fig.8 Structure chart of traditional ip-iqharmonic detection algorithm
在传统ip-iq谐波检测算法中,检测效果一般取决于PLL锁相精度和LPF滤波效果,当电网质量复杂时,例如电网频率突变、含直流成分和多次谐波,PLL锁相将会出现误差,LPF也不能滤除直流成分和低次谐波,将严重影响ip-iq谐波检测算法的检测效果。
2.2 基于IFFSOGI的ip-iq谐波检测算法
本文利用IFFSOGI-PLL为ip-iq法提供更准确的电网频率,精确锁相电网电压相位,同时利用IFFSOGI滤除信号中的直流成分和各次谐波,得到更准确的基波电流信号,最后电网三相电流与基波电流相减,得到电网中谐波信号。所提出的ip-iq谐波检测算法结构如图9所示。

图9 基于IFFSOGI的ip-iq谐波检测算法结构图Fig.9 ip-iqharmonic detection algorithm structure chart based on IFFSOGI
3 仿真分析
为验证本文所提方法的有效性,在Matlab/Simulink中搭建IFFSOGI-PLL和基于IFFSOGI改进型ip-iq谐波检测算法模型,分别在电网频率突变、电网含直流成分和多次谐波等条件下与SOGI-PLL和传统ip-iq法进行对比研究。
为验证电网频率突变时FFSOGI的有效性和IFFSOGI-PLL锁相效果,在时间为0.2 s时电网电压频率突变至60 Hz,仿真结果如图10所示。由图10a、图10b可知,在电网频率突变时,SOGI输出正交信号幅值并不相等,而FFSOGI能够输出幅值相等的正交信号,从而验证了FFSOGI的有效性。由图10c可知,在电网频率突变时,SO-GI-PLL输出频率在11.4 ms内首次达到60 Hz,在20 ms内达到峰值,超调量为4.13%,在53 ms内频率恢复稳定,频率误差为0。IFFSOGI-PLL输出频率在8.8 ms内首次达到60 Hz,在11.8 ms内达到峰值,超调量为1.47%,在27 ms内频率恢复稳定,频率误差为0。因此,IFFSOGI-PLL动态响应速度较好,产生的超调量更小,能准确锁相。

图10 频率突变时仿真结果Fig.10 Simulation results with frequency mutation
为验证在含直流成分时基于IFFSOGI的改进型ip-iq谐波检测算法的有效性,向电网中注入10%的直流电压、10 A直流电流,仿真结果如图11所示。由图11a可知,电网含有直流成分时,SRF-PLL和SOGI-PLL输出频率发生振荡,无法准确锁定电网频率,IFFSOGI-PLL能够在55 ms内快速锁定电网频率。由图11b、图11c可知,电网电流中含有多次谐波和直流成分,波形畸变率THD为25.03%,电流波形发生严重畸变。由图11d和图11e可知,传统ip-iq法能够滤除电流中的部分高次谐波,输出波形中含有直流成分和多次谐波,波形畸变率THD为6.96%,输出电流越靠近基波,最后与电网三相电流做差得到的谐波才能更准确,说明谐波检测效果越好,基于IFFSOGI的改进型ip-iq法输出电流波形畸变率仅为0.17%,且直流成分和各次谐波几乎滤除,因此验证了所提方法的优越性。

图11 含直流成分时仿真结果Fig.11 Simulation results with DC component
为验证在含多次谐波时基于IFFSOGI的改进型ip-iq谐波检测算法的有效性,向电网A相电压注入5%的5次正序谐波和B相电压注入5%的7次正序谐波,仿真结果如图12所示。

图12 含多次谐波时仿真结果Fig.12 Simulation results with multiple harmonics
由图12a可知,电网含有多次谐波时,SRFPLL和SOGI-PLL输出频率发生振荡,其中SRFPLL振荡更为严重,IFFSOGI-PLL能够在80 ms内快速锁定电网频率,受电网谐波影响较小。由图12b、图12c可知,电网电流中含有多次谐波时,三相电流波形均发生严重畸变,波形畸变率为20.58%。由图12d、图12e可知,传统ip-iq法输出波形中仍含有多次谐波,波形畸变率THD为3.32%,基于IFFSOGI的改进型ip-iq法输出电流波形畸变率仅为0.23%,且各次谐波几乎滤除,因此验证了所提方法的优越性。
图10~图12仿真实验波形表明:
1)频率突变时,SOGI-PLL和IFFSOGI-PLL均能锁定电网频率,但是IFFSOGI-PLL锁相调节时间更短、动态响应更快、超调量更小;
2)在含直流成分和多次谐波时,SRF-PLL和SOGI-PLL无法准确锁相,在基波频率附近发生周期振荡,IFFSOGI-PLL能够准确锁相,为ip-iq法提供更准确的电网角频率;
3)在含直流成分和多次谐波时,传统ip-iq谐波检测法能够滤除部分高次谐波,但受直流成分影响较大,基于IFFSOGI的改进型ip-iq谐波检测法能够滤除直流成分和多次谐波,波形畸变率更小,检测效果更好。
4 结论
针对电网存在频率突变、直流成分和多次谐波时,传统ip-iq谐波检测算法无法准确检测电网中谐波问题,提出一种基于改进固定频率二阶广义积分器的ip-iq谐波检测算法,经理论分析和仿真验证,得到以下结论:
1)IFFSOGI能够克服传统SOGI输出正交信号不等幅问题,能够滤除信号中直流成分和多次谐波;
2)IFFSOGI-PLL能够在电网存在频率突变、直流成分和多次谐波时准确锁相,为ip-iq谐波检测算法提供更准确的电网频率;
3)基于IFFSOGI的改进型ip-iq谐波检测算法能够在电网存在直流成分和多次谐波时输出电流畸变率小,谐波检测效果较好。

