无/缺水下地形数据的高原堰塞湖水量遥感估算

朱长明，张新，方晖，王伟胜

1.江苏师范大学 地理测绘与城乡规划学院,徐州221116;

2.中国科学院空天信息创新研究院 遥感科学国家重点实验室,北京100101;

3.中国科学院新疆生态与地理研究所,乌鲁木齐830011;

4.中国科学院中亚生态与环境研究中心,乌鲁木齐830011;

5.中国科学院大学,北京100049

1 引 言

堰塞湖蓄水量是决定堰塞湖溃决风险大小的最为关键性因子（黄艳等，2019；王杨科等，2013；谢建丽，2013）。通常来说堰塞湖蓄水量越多安全性威胁越大，溃决洪水冲击力越危险，带来的自然灾害越严重（匡尚富等，2008；刘宁等，2016；吕杰堂等，2002）。因此，实时监测高原堰塞湖库区蓄水量动态对于堰塞湖的险情评估、灾害推演、安全管理以及降险处置决策等均具有重要的意义（匡尚富等，2008；刘宁等，2016）。传统的湖泊水量计算主要有测绘学方法和水力学方法，分别基于图上地形量测和基于实地水文观测模拟（曹波，2006；甘拯等，2017；米鸿燕等，2007；童思陈和周建军，2003）。具体计算方法上可以概括为两大类：（1）直接计算静库容代替总库容，相关算法有网格法、等高线法以及横断面法等（高圣益和李成国，2007；米鸿燕等，2007）；（2）基于简化河槽形态和实测数据，采用水文动力学模型计算总库容，这种算法包括了动库容和静库容（Furnans 和Austin，2008；秦惠承，1983；许海军和陈守煜，2002）。图上测量要求有较为详细的湖泊地形资料，水文动力学模型则需参数较多、计算耗时较长，时效性较差；导致了传统水量监测技术手段通常难以满足应急抢险救灾的时效性需求。所以堰塞湖水量准实时快速精准监测一直是堰塞湖风险评估中的一个技术难点。

随着空间对地观测信息技术的发展，水量遥感定量估算与动态监测已经成为水文遥感研究的重要内容，在应急、抢险和救灾中彰显了突出的技术优势（陈晓玲等，2008；黄诗峰等，2013；谢建丽，2013；朱长明等，2015）。目前水量遥感计算模型主要有统计经验模型和物理量测模型两大类。统计经验模型是通过实测数据建立水位面积库容曲线，再根据实时遥测面积或者水位信息估算出湖泊 水量（Zhang 等，2014；Duan 和Bastiaanssen，2013）。如：吕杰堂等（2002）通过湖泊的面积和库容的关系计算了西藏易贡滑坡堰塞湖库容；田雨等（2017）利用实地水文统计数据，建立水库面积—库容模型，完成雪野水库库容量的测算；Duan 和Bastiaanssen（2013）通过库容曲线协同测高卫星和遥感影像反演出动库容。而物理量测模型是通过实时遥感数据匹配高精度的水下地形数据，直接从地形图上定量计算出湖泊水量（蔡青等，2012；曹波，2006；刘东和李艳，2012）。但是，从现有的文献来看目前水量遥感计算模型主要是面向湖盆水下地形数据或者库容曲线已知的情况。然而，针对高原无/缺资料区突发性地质灾害形成的堰塞湖，可用基础资料异常匮乏，基本上没有详细的水下地形数据；加上应急处置的急迫性、区域地质环境的复杂性和现场监测的困难性，很难在较短时间内获取得到高精度的水下地形数据，这给水量遥感定量动态监测带来了挑战。故，如何在缺少水下地形数据的情况下，快速准确地获取堰塞湖水量数据是需亟待解决的技术难题。

为此，本文提出了一种无/缺水下地形数据的高原堰塞湖水量遥感快速定量测算方法，实现了水下地形特征数据不完备的高原地区堰塞湖水量遥感测算问题，为无水下地形数据的高原堰塞湖水量遥感快速估算提供了一种有效的方法。

2 研究区与数据源

2.1 研究区介绍

实验选取帕米尔高原百年堰塞湖—萨雷兹堰塞湖为主要研究区（图1），地处帕米尔高原东部穆尔加布河谷，38°10′N—38°20′N，72°30′E—73°10′E，形成于1911年的一场强烈地震。由于地震引起巨大山体滑坡，堵塞了东西走向的穆尔加布河道，水位快速上升形成了高原堰塞湖。其中乌索伊大坝就是滑坡体堆积形成的天然坝体。

图1 研究区Fig.1 Study area

萨雷兹堰塞湖集水面积超过16000 km2，水域淹没面积约80 km2，长度约60 km，平均宽度约1.44 km，最深处超过了500 m，不断上升的水位严重威胁着下游的重要基础实施和数百万群众的生命财产安全（杨立信，2008a；Ischuk，2011）。萨雷兹湖安全问题及风险监测引起了当地政府和国际社会的广泛关注，一旦溃决或引发洪水必将是一场空前生态大灾难，曾被英国《焦点》杂志列为全球十大潜伏的致命性自然灾害（杨立信，2008b）。但是，区域交通可通达性差、地质环境恶劣，实地地形测量和水文信息采集非常困难，详细的水下地形资料缺乏，导致堰塞湖水量动态监测和风险评估技术难度较大。本文试图通过空天遥感信息技术完成水下地形数据未知的萨雷兹湖水资源量定量估算，为萨雷兹湖风险监测和预报预警提供技术支撑。

2.2 数据源选择

实验地面高程数据主要来源于美国NASA 和日本METI 共同发布的先进星载热发射和反射辐射仪全球数字高程模型ASTER GDEM V003（Advanced Spaceborne Thermal Emission and Reflection Radiometer Global Digital Elevation Model），数据获取时间是2000年—2009年，空间分辨率为30 m，经多次校正，正式发布于2019-08（数据下载：https：//cmr.earthdata.nasa.gov/search/concepts/C1299783579-LPDAAC_ECS.html［2021-04-15］）；堰塞湖水域面积监测主要采用了美国陆地资源卫星Landsat 系列遥感数据。堰塞坝区高精度数据来自中国科学院新疆生态与地理研究所的无人机倾斜航拍数据，数据获取时间：2017-07-30—31。由于涉及湖泊水域面积计算和体积估算，将数据统一转换为阿尔伯斯等积圆锥投影。

3 堰塞湖水量遥感快速估算方法

无/缺水下地形数据的高原堰塞湖水量遥感定量估算方法技术流程见图2。整体技术流程包括水域淹没面积提取、多边形中线确定、特定点河道高程获取、局部河道比降计算、水下地形拟合和三维曲面离散积分等6个模块。

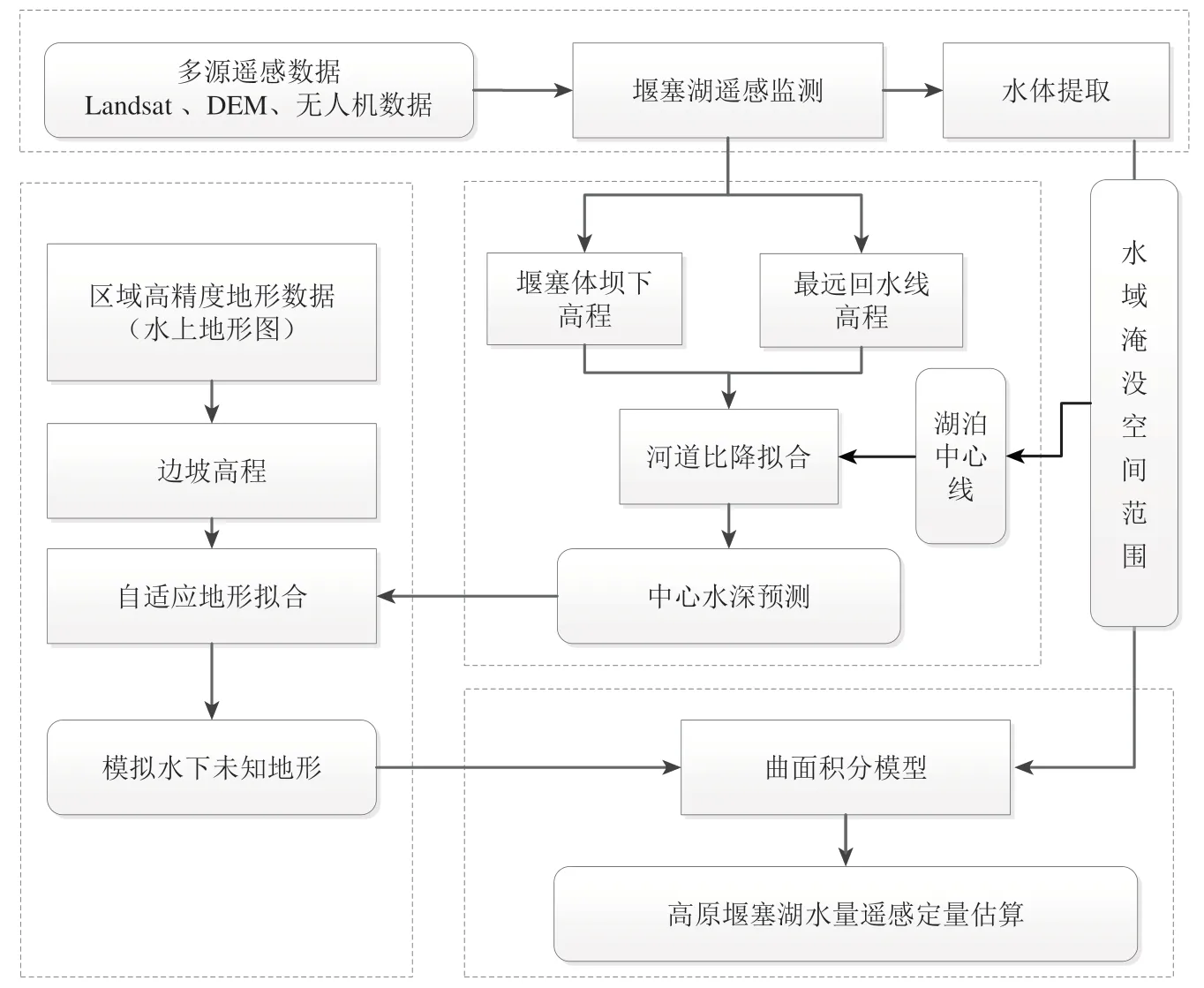
图2 无水下地形的堰塞湖水量遥感估算方法流程Fig.2 Flow chart for dammed lake water volume estimation at underwater topographic data unknown

首先是基于光学遥感的提取水域淹没面积，获取堰塞湖水域分布和坝体以及最远回水线位置；然后，通过泰森多边形Delaunay准则计算到河岸两边离散点距离相等的点集，标识出河道中心线；进而，根据坝前高程、最远回水位的河道中心高程估算河道局部比降系数，并据此推算出分段河道中心点高程，作为水下地形模拟的约束因子；通过左右边坡的高程信息并结合河床中心线高程约束因子构建河道已知高程集合；在此基础上进一步通过地形拟合自适应模拟出堰塞湖水下未知地形；最后，结合实时淹没面积通过三维曲面离散积分快速计算堰塞湖蓄水量。

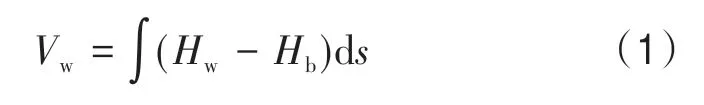
式中，Vw为湖泊总蓄水量，Hw为湖泊水面高程，Hb为湖泊水低高程，ds为微分单元面积。对于空间栅格数据来说，离散曲面积分可以进一步表示为式（2）。

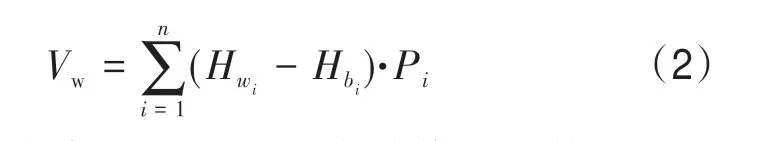
式中，n为堰塞湖淹没的所有水域像元总数量，Pi为单个像元面积，Hwi为第i个像元的湖面水位高程，Hbi为第i个像元的水下地形高程。

其中，河道的局部比降系数估算，由于数据有限，采用了线性拟合的方法。根据坝体下的河床高程和最远回水位置河床高程，拟合局部河道的比降系数，计算公式具体为

式中，S为河道的局部比降系数，A为坝体下的河床高程，B为最远回水位置河床高程，D（）为两点的距离。

4 方法验证与评估

为验证算法的有效性和定量估算结果的真实可信性。文章选取了穆尔加布河支流已知地形的河道作为实验验证区，见图1中的标注。假设河道被堰塞，模拟水位上涨到3450 m，根据水上地形和该段河道的比降，按照文中的方法去预测水下地形，结果见图3。从图3的DEM 晕渲图上看，模拟结果基本能够很好地呈现出堰塞河道水下地形。进一步量化评估模拟水下地形的精度，表1从定量统计的角度，将模拟数据与真实数据进行了对比。真实数据和模拟数据的各项定量统计指标（如：均值、方差、值域范围等）吻合度较高，相关系数达到0.95以上，误差均值约1.29 m。

表1 模拟数据与参考数据相关统计量对比Table 1 Quantitative comparison of correlation statistics between simulated data and reference terrain

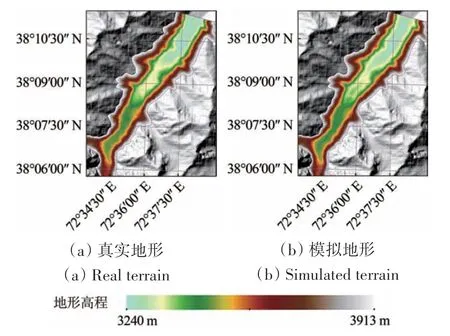
图3 局部区域水下地形模拟对比验证实验Fig.3 Comparison between simulated underwater terrain with measured values

图4显示了不同的淹没水位堰塞湖水量统计计算模拟，绘制了两种情况的库容曲线。其中真实库容曲线是通过真实地形数据测算，模拟库容曲线是用文中模拟水下地形方法估算。从库容曲线的结果对比来看：本文中的方法基本上能够精确地反演出堰塞湖的库容量，模拟值与真实值在各个水位段上均保持高度一致，相关系数达到了95%（P＜0.01），最大误差控制在10%范围之内，证明了该算法的有效性和估算结果的可信度。

图4 模拟库容与真实库容比较Fig.4 Comparison between simulated volume and actual volume

5 方法的应用

5.1 萨雷兹湖水量估算

根据上述方法首先模拟出萨雷兹堰塞湖的水下未知地形（图5）。从水下地形模拟图上可以看出，整个萨雷兹湖湖盆呈现东高西低的趋势；最深处在河流下游距离乌索伊大坝前的一段距离处，最深处湖底高程约为2750 m 左右。结合2018年夏季的卫星遥感影像水域掩模面积，当前坝前水位约为3268 m，由此可以得知萨雷兹湖最深处水深已经愈520 m。

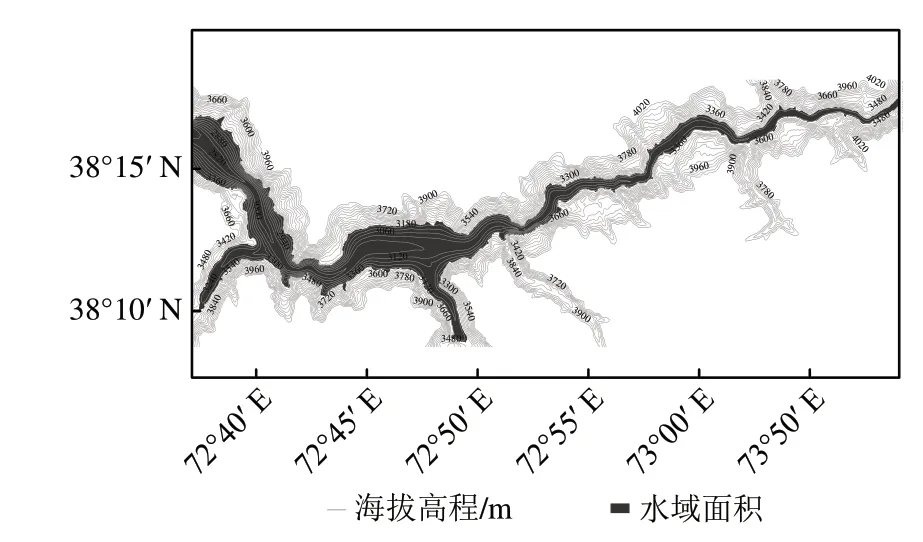
图5 萨雷兹堰塞湖水下地形模拟图Fig.5 Simulation underwater terrain of Sarez lake

根据这一模拟水下数字地形高程模型数据，结合水域淹没空间范围，通过离散曲面积分计算得到萨雷兹湖当前的蓄水量约为162.49 亿m³。这一计算结果与现有的文献资料估测水量数据（最大水深超过500 m，蓄水量约为155—165亿m³）基本吻合（杨立信，2008a）。

5.2 水量动态变化分析

基于研究区域1972年以来的Landsat 存档遥感数据，从中挑选了质量较高的遥感影像，提取了1972年—2018年萨雷兹湖的水域淹没面积分布。在此基础上，结合模拟的水下地形数据，采取曲面积分的方法定量计算了萨雷兹湖的水资源库容量，并绘制萨雷兹湖的面积—水位—库容关系曲线，见图6。

图6 萨雷兹湖水位-面积-库容模型Fig.6 Water level-area-storage capacity model of Sarez Lake

6 结 论

本文提出了一种无/缺水下地形资料的高原堰塞湖水量遥感快速估算方法，该方法能够快速估算高原堰塞湖水量，算法精度较高技术通用性强，初步实现了水下地形数据未知的高原堰塞湖水量遥感估算过程中的变量特征不完备难题，为无/缺资料区高原堰塞湖水量遥感快速监测提供了一种可行的技术方法，应用前景较为广阔。研究得到以下结论：

（1）无/缺水下地形数据的高原堰塞湖水量遥感估算方法减少了遥感水量估算对水下实测地形数据的依赖，为水下地形难以获取的高原堰塞湖水量遥感定量估算提供了可行的方法；

（2）无/缺水下地形数据的高原堰塞湖水量遥感定量估算有效规避了传统水文学算法中静态库容和动库容纠缠，降低了计算成本提高了信息获取时效性，可适应快速应急响应监测要求。

实时动态水量遥感监测是防治堰塞湖次生灾害发生过程中的一个技术难点。文章虽基本实现了无/缺水下地形数据的高原堰塞湖水量遥感定量估算方法；但本算法模型仍然有需要改进和完善的地方。例如：淹没面积提取可以考虑采用更高精度的卫星数据源如GF-1/2、GF-3 等，边坡高程受GDEM 数据的精度影响，可以进一步考虑无人机高精度三维立体测图数据。另外需要指出的是由于文中受数据获取的限制，对河流的比降系数采取了线性估算，但对于大区域来说可能会对模拟精度有直接的影响。随着可利用遥测数据源增多，未来可以考虑多点采样的非线性比降拟合模型。例如：机载激光测深系统和无人船水下测量相结合，对水下地形分段抽样测量加密，可进一步提高预测模型的精度。