一类Hilfer分数阶Riemann-Stieltjes积分边值问题解的存在性
蒋方园,徐家发,柏仕坤
重庆师范大学数学科学学院,重庆,401331
文本运用不动点方法研究如下高阶Hilfer分数阶Riemann-Stieltjes积分边值问题解的存在性:
(1)
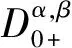

众所周知,分数阶微分方程因其在人口动力学、记忆材料热传导、渗流等许多重要应用领域的应用而受到广泛关注,例如文献[1]中提到了一种各向同性、齐次、有耗介质中,平面电磁波传导模型,其一维方程为
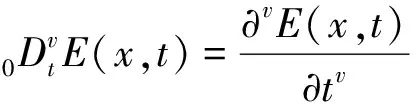
近年来,Hilfer给出了一种广义的Riemann-Liouville分数阶导数,称之为Hilfer分数阶导数,其可包括传统的Riemann-Liouville型和Caputo型分数阶导数,对于该类分数阶模型的研究亦开展起来了,参见文献[5-13]及其所附参考文献。我们注意到在已有文献中很难发现所研究的Hilfer型分数阶微分方程模型能被准确地表达成Hammerstein型积分方程,这会给研究该类方程带来一定的困难(因被转换的积分方程形式过于复杂)。文本就是克服这一困难,运用Green函数和不动点的方法研究问题(1)解的存在性和唯一性,并给出唯一解的迭代格式。最后,提供两个例子支撑我们的结论。
1 预备知识
首先给出本文所需要的有关Hilfer分数阶的定义和基本结论,详细内容可参见文献[2-17]。
定义1函数g:+→的α(>0)阶Riemann-Liouville分数积分定义为:
定义2函数g:+→的α(>0)阶Riemann-Liouville分数导数定义为:
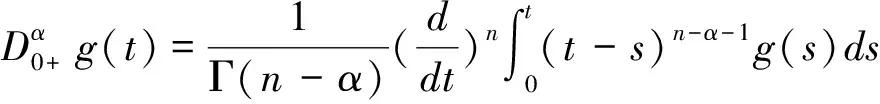
定义3令α∈(n-1,n),β∈[0,1],n∈+,则函数g(∈L1[0,1])的Hilfer分数阶导数为:
注意到上式亦可以表达为:
θ=α+nβ-αβ
由上述定义我们可得如下的性质:
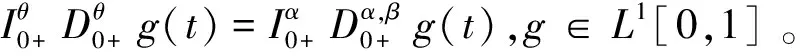
性质2若n-1<α 文本的思路是将问题(1)转换成等价的积分方程,为此需要计算问题(1)对应的Green函数。考虑如下的辅助问题: 引理3若(H0)成立。令h∈C[0,1],则边值问题 (2) 的解可表达为: (3) 其中 (4) (5) 证明:根据引理2可得 其中,ci∈,i=1,2,…,n。 由条件u(0)=u′(0)=…u(n-2)(0)=0知: c2=…=cn=0 从而 (6) 借助(H0)可解得: 证毕。 引理5函数G有以下的性质: i)G(t,s)∈C([0,1]×[0,1],+); 该结论是引理4的直接结果,故略去其证明。 (7) 其中,G见引理3。若令f是[0,1]×上的连续函数,则加上G的连续性我们可知算子A是一全连续算子,并且若存在u*∈E{0}使得Au*=u*,则u*是算子A的非平凡不动点,即是问题(1)的非平凡解。 在以下的结论中,假定f(t,0)≠0,t∈[0,1],即0不是A的不动点,后面讨论中不再赘述。 定理6若(H0)和以下条件成立: H1)f∈C([0,1]×+,+), H2)f关于第二个变量u是增函数,即若u1≤u2,则f(t,u1)≤f(t,u2),∀t∈[0,1] ≤tθ-1φ(s),t,s∈[0,1] (8) 根据(H3)可得存在ε1∈(0,Λ1),c1>0使得 f(t,u(t))≤(Λ1-ε1)u(t)+c1,u≥0,t∈[0,1] (9) 令u0(t)=Mtθ-1,t∈[0,1],则Au0≤u0.定义序列 un+1=Aun,n=0,1,2,… (10) 下证该序列为递减序列。 事实上,u1=Au0≤u0,从而根据(H2)可得: 假设uk≤uk-1,k=1,2,…,则由(H2)知: Au*=u* 前述已指出0不是A的不动点,从而u*是A的正不动点,即是问题(1)的正解。证毕。 以下将问题(1)稍作变形,即研究如下问题: 其中φ:[0,1]→,φ∈L1[0,1],且φ在[0,1]的任何子区间上不恒为0。 定理7若(H0)和以下条件成立: (H4)f∈C([0,1]×,); (H5)存在σ∈[0,1],使得∀t∈[0,1],u,v∈,有|f(t,u)-f(t,v)|≤σκ-1|u-v|, 其中κ见引理5。 则问题(11)存在唯一的非平凡解u*,并且对任意的u0∈E,u0≠0。迭代序列un=Tun-1(n=1,2…)收敛到u*,其中 证明:对任意的u0∈E,u0≠0,令un=Tun-1(n=1,2…)根据算子T的全连续性,该序列属于E.从而对任意的正整数n,根据引理11,有 |un+1(t)-un(t)|=|(Tun)(t)-(Tun-1)(t)| -f(τ,un-2(τ))|dτds ≤… -f(s,u0(s))|dsdt 从而可得: ×|u1(t)-u0(t)|dt (12) 再由(12)式可得: |un+1(t)-un(t)|≤σnΓ(α+2)β0从而对任意的正整数m,n,可得: |um+n(t)-un(t)|=|um+n(t)-um+n-1(t) +um+n-1(t)-um+n-2(t)+…+un+1(t)-un(t)| ≤|um+n(t)-um+n-1(t)|+|um+n-1(t) -um+n-2(t)|+…+|un+1(t)-un(t)| ≤β0Γ(α+2)(σm+n-1+σm+n-2+…+σn) 在等式两边同时取极限可得u*=Tu*,即u*是算子T的非平凡不动点,即问题(11)存在一个非平凡解。 下证该解是唯一的。若存在v*使得Tv*=v*,u*≠v*,则对任意的正整数n,有Tnu*=Tn-1(Tu*)=Tn-1u*=···=u*,Tnv*=v*。 进一步可得: |u*(t)-v*(t)|=|(Tnu*)(t)-(Tnv*)(t)| =|T(Tn-1u*)(t)-T(Tn-1v*)(t)| -f(s,(Tn-1v*)(s))|ds -(Tn-1v*)(s)|ds -(Tn-1v*)(t)|dt -T(Tn-2v*)(t)|dt -f(s,Tn-2v*)(s)|dsdt -(Tn-2v*)(s)|ds -(Tn-2v*)(t)|dt ≤… -(Tv*)(t)|dt -f(s,v*(s)|dsdt 此即表明 (13) 注1:文献[14]中作者运用单调迭代方法研究了如下Riemann-Liouville型分数阶积分边值问题正解的存在唯一性: 其中α∈(2,3],满足如下的单调有界条件: 存在χ>0使得f(t,x)≤f(t,y)≤Θχ,∀0≤x≤y≤χ,t∈[0,1],其中Θ是一正常数。 显然文本的(H3)包含这一条件,我们仅要求非线性项关于未知函数在无穷远处次线性增长即可,而不需要单调有界这样更强的条件。 注2:运用u0-正算子的方法研究了如下Riemann-Liouville型分数阶边值问题非平凡解的存在唯一性[15]: (15) 其中p∈(2,3],f满足如下的Lipschitz条件: 存在σ∈(0,1)使得|f(t,u)-f(t,v)|≤σλ1|u-v|,∀t∈[0,1],u,v∈,其中λ1是式(15)对应的线性问题的第一特征值。 虽然定理13的条件和结论与文献[15]类似,然而我们仅用到完备空间中的Cauchy列收敛这一基本原理,并且不需要用更复杂的理论去计算线性问题对应的特征值(实际上算不出来具体值)。这对于初学者更易学易懂。 例1令f(t,u)=Λ2uϑ+ρ(t),u∈+,t∈[0,1],其中ρ是[0,1]上的非负连续函数且在[0,1]上不恒等于0,Λ2∈(0,Λ1),ϑ∈(0,1]。则该函数关于u单增,且 对t∈[0,1]一致成立。定理12的条件均满足。 例2令f(t,u)=σΛ3u+ψ(t),其中ψ是[0,1]上的连续函数且在[0,1]上不恒等于0,Λ3∈(0,κ-1]。则|f(t,u)-f(t,v)|≤σΛ3|u-v|≤σκ-1|u-v|,∀t∈[0,1],u,v∈。 从而定理7的条件均满足。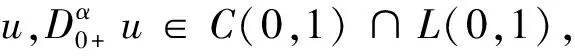
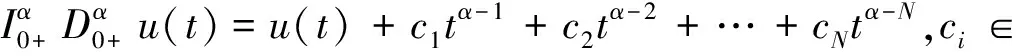
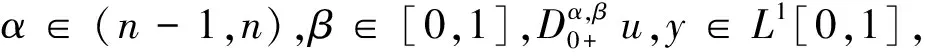
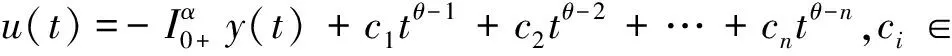



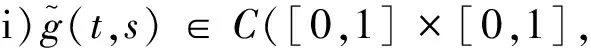

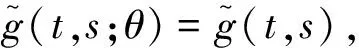
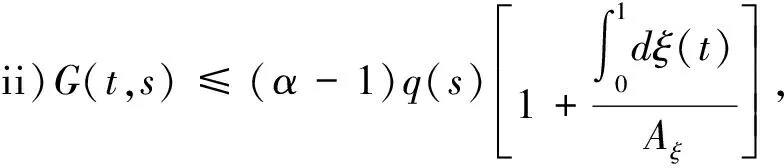

2 主要结论
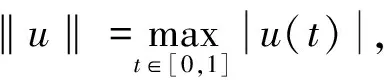

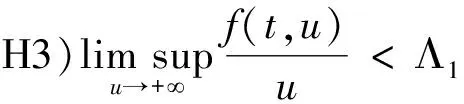



















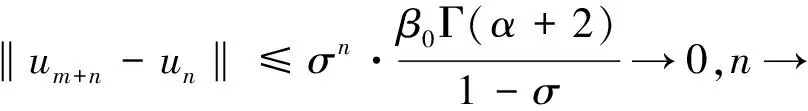









3 例 子

