基于新能源电动汽车复合电源能量管理的模糊控制研究

高俊岭，丁 昇，张 翔

安徽理工大学电气与信息工程学院,安徽淮南,232001

1 引 言

日益严峻的能源危机与环境污染等问题加速新能源产业的发展，在汽车领域，电动汽车的改进、升级成为研发人员和学者的重点研究对象。电动汽车的动力主要由蓄电池提供。但由于单一的蓄电池功率密度小，在车辆行驶过程中很难完全满足车辆所需的能量和功率双重需求，因此很大程度上限制了电动汽车行业的发展。近年来，因充放电速度快、功率密度大等显著特点，超级电容得到快速发展[1]。

将超级电容引入电源系统，用于向电机提供瞬时大功率和回收制动时电机所产生的能量，起到“削峰填谷”的作用。在保证车辆续航里程的同时，增强了电动汽车的动力性能，避免蓄电池因频繁地充放电和瞬时大电流的冲击而受到损坏，在一定程度上延长了蓄电池的使用寿命。因此，将超级电容引入电源系统，构成复合电源(Hybrid Energy Storage System，HESS)，具有较高的研究价值[2]。关正等[3]采用PI电压电流双闭环控制方法，来实现对电源输出功率的控制，但系统受扰动影响较大，直流母线抖振较为严重。Samosir[4]用传统的线性控制策略，简单容易实现，但由于复合电源系统属于非线性系统，因此该策略不够稳定。赵国柱等[5]在分析复合电源工作原理的基础上，基于保护蓄电池的原则设计了模糊逻辑能量管理策略，但主要集中在对需求功率的分配上，对于控制电源功率输出的DC/DC变换器的控制方法未做详细设计。

基于此，文本根据车辆运行过程中的车速、蓄电池和超级电容剩余电量的变化设计模糊控制策略，合理分配需求功率；在模糊控制策略的基础上，同时引入一种新型趋近律滑模控制策略控制电源功率的输出，减少误差扰动的影响，提高控制系统的响应速度，抑制抖振。从而形成一种全新的模糊-新型趋近律控制策略，以此达到提高控制电源功率输出精度的目的。

此策略的控制目标为：(1)维持直流母线电压稳定；(2)超级电容器的输出电流能够准确跟踪参考电流。从而使得HESS能够更加合理地将需求功率分配给蓄电池和超级电容，根据车辆行驶状态及时做出动态调整。

2 系统结构及工作模式分析

2.1 HESS电路结构

HESS系统由主电源蓄电池、辅助电源超级电容组、DC/DC变换器和功率分配其控制系统构成。系统简化结构如图1所示。

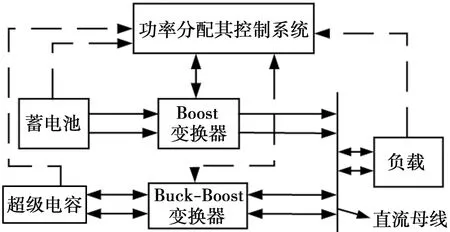
图1 HESS电路结构

蓄电池通过Boost变换电路连接至直流母线，超级电容通过Buck-Boost双向变换器连接至直流母线，两者并联连接。功率分配及其控制系统根据实时车速计算出需求功率，同时结合超级电容的荷电状态(SOCSC)，判断出系统的工作模式，进而调用相应的控制策略来控制两组变换器开关的导通与关断，从而实现对电源系统功率输出的控制。

2.2 HESS工作模式分析

根据路面状况的实时变化，车辆需要频繁地加减速。因此，电动汽车的运行状态可分为驱动和制动两种状态：驱动状态可分为蓄电池单独供电、蓄电池和超级电容共同供电两种状态；制动状态可分为回收和消耗制动能量两种状态。

(1)当车辆平稳运行、需求功率较小时，由蓄电池单独供电；当车辆需求功率大时，此时超级电容组介入工作，与蓄电池构成“双电源供电”状态。

(2)当车辆处于减速制动状态、SOCSC未达上限时，电机因制动所产生的能量由超级电容回收；当车辆处于减速制动状态、超级电容荷电状态已达上限时，此时为了避免超级电容过冲，有良好的制动效果，由能耗电阻消耗制动能量。

3 系统电路分析与建模

3.1 系统电路分析

图2为复合电源等效电路。蓄电池是车辆的能量来源。Boost变换器[6]主要负责将蓄电池输出电压升至直流母线电压参考值。其中，μ1为全控性开关器件IGBT S1的开关驱动信号。超级电容主要用于向电机提供瞬时大功率和回收制动时电机所产生的能量。Buck-Boost变换器负责当超级电容输出功率时将输出电压升至直流母线电压参考值，当超级电容回收制动能量时将电压降至超级电容两端目标电压值。μ2和μ3分别为全控性开关器件IGBT S2和S3的开关驱动信号。负载系统由全控性开关器件IGBT S4-S9和电机M构成。

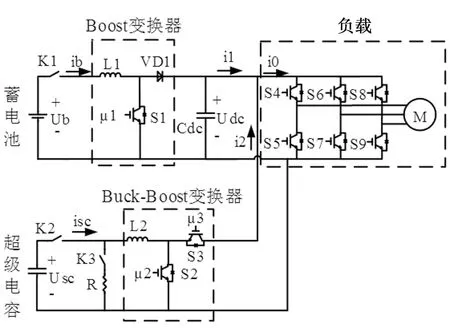
图2 HESS等效电路

为了充分发挥HESS的优势，本文针对HESS结构采用一种新型趋近律滑模控制策略。图2中采用目标电压和电流双闭环控制策略对Boost变换器控制，这样既能稳定直流母线的电压，又能控制蓄电池的输出电流。

3.2 系统建模

图2中，蓄电池两端电压为Ub；输出电流为ib；i1为Boost变换电路的输出电流；Udc为负载端电压；超级电容的端电压和输出电流分别为Usc和isc；i2为Buck-Boost变换电路的输出电流；i0为负载电流，其值为两个变换电路输出电流i1、i2之和。

对于蓄电池和Boost变换电路部分的电路，根据基尔霍夫定律列写关系式，如式(1)所示，其中IGBT S1的开关驱动信号μ1的数值在(0，1)之间。

(1)

对于超级电容和Buck-Boost变换电路部分，当超级电容处于供电状态时(P> 0)，Buck-Boost变换电路工作模式为Boost变换电路；当超级电容处于充电状态下时(P< 0)，Buck-Boost变换电路工作模式为Buck变换电路。因此定义一个变量k，k的表达形式为：

(2)

当k=1，μ3=0时，S3不工作，S2在PWM控制信号μ2的控制下工作；当k=0，μ2=0时，S2不工作，S3在PWM控制信号μ3的控制下工作。

列写关于超级电容和Buck-boost变换器组成电路的全局状态关系式，即：

(3)

4 HESS控制策略研究

4.1 能量管理策略

研究采用的控制策略是通过模糊控制策略将需求功率合理地分配给蓄电池和超级电容，通过新型趋近律控制方法精确控制变换器的导通与关断，进而实现输出功率精确跟随参考功率。如图3为模糊控制器的控制逻辑流程，输入信号由三个信号参数构成，分别为需求功率Preq、超级电容荷电状态SOCSC和蓄电池荷电状态SOCbat。需求功率Preq是由车速v计算得出(公式下文会具体给出)。超级电容输出功率在总功率中所占的比值a，取值区间为[0，1]。模糊控制器的输入输出变量的子集及其各自的隶属度函数如图4所示。

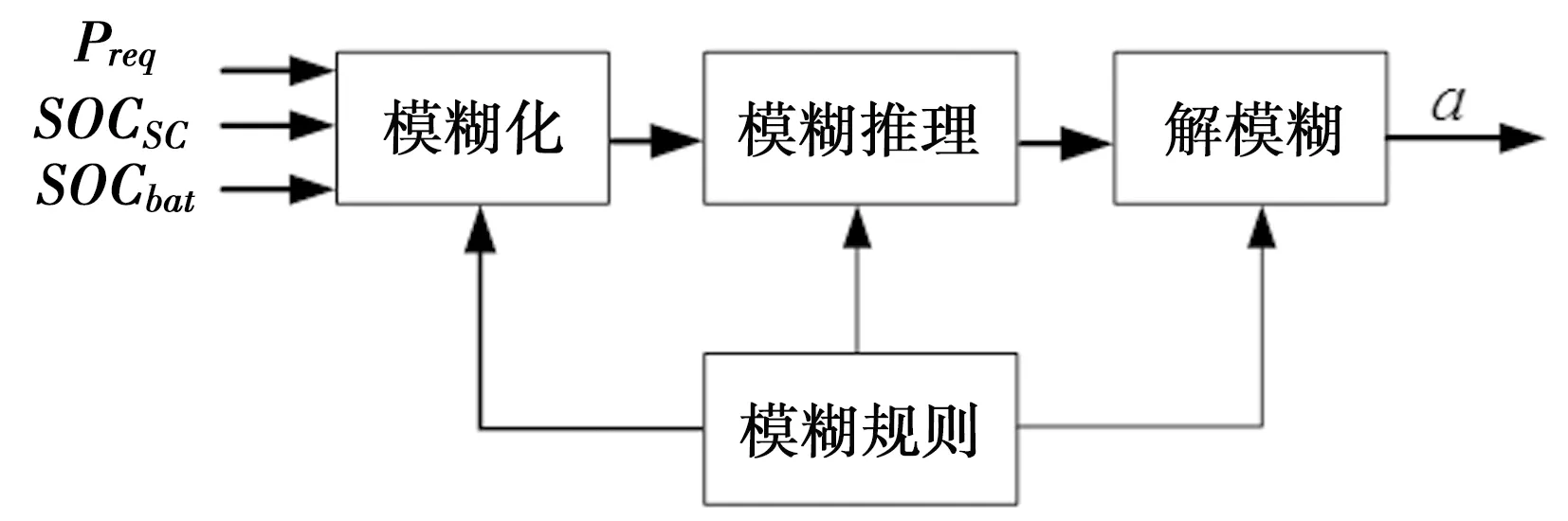
图3 模糊控制逻辑图

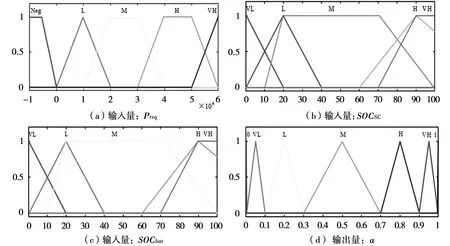
图4 模糊控制器各变量隶属度函数

模糊控制器的设计原则为：通过Preq判断车辆是驱动(Preq> 0)或者制动(Preq< 0)状态，当Preq< 0时，还需评估SOCSC的大小。VH状态视为超级电容电量已满，此时超级电容不再回收制动能量，改由能耗电阻消耗制动能量；除此之外，超级电容回收制动能量。当Preq> 0时，还需要判断SOCSC的大小。当SOCSC处于0状态时，视为超级电容能量已耗尽，此时蓄电池单独共工作，为负载提供能量；其余状态下，根据SOCbat和SOCsc合理分配输出功率，此时蓄电池和超级电容同时为负载提供能量。

根据设计原则，结合模糊控制器的变量子集，共设有125条模糊规则，部分规则见表1。

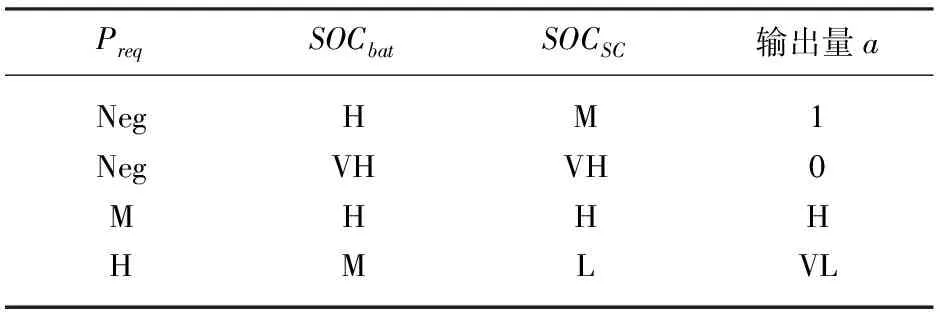
表1 部分模糊控制规则

考虑到车辆自身参数和车辆行驶过程中受到的四种阻力以及传输、转换效率来计算车辆需求功率[7]。需求功率P由式(4)得：

(4)

其中，ηD为DC/DC变换器传输效率；ηT为机械传动效率；ηI为电机能量转换效率；f为滚动阻力系数；m为电动汽车整体质量；g为重力加速度；α为道路的坡度，假设行驶过程中坡度为0；CD为空气阻力系数；A为汽车迎风面积；ρ为空气密度；v为车速。

汽车的滚动阻力系数f可根据文献[8]的经验拟合公式：

f=0.042 4v2+1.376 1v+154.74

(5)

4.2 控制策略设计

4.2.1 新型趋近律

与传统的PI调节相比，滑模控制响应速度更快、动态性能更优越、参数的变化和扰动影响更小。因此，将滑模控制应用于DC/DC变换器是可行的。在此基础上，提出一种新型趋近律，此新型趋近律拥有更高的趋近速度，同时能够抑制滑模变结构中固有的抖振现象[9]。新型趋近律具体形式为：

(6)

式中：eq()为指数函数；sgn()为符号函数；s为系统滑模面；X1为误差值，为系统状态变量；k、ε、η、δ皆为趋近律参数。

4.2.2 Boost变换器控制策略

取电压误差X1、电感电流误差X2作为受控状态变量：

[x1,x2]=[Udc-ref-Udc，IL1-ref-IL1]

(7)

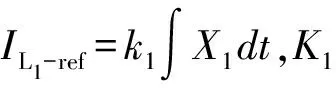
S=X2

(8)

对式(8)求偏导得：

(9)

为了保证滑模状态存在，必须满足：

(10)

根据式(6)设计控制器，将式(1)带入式(9)，结合式(6)，可求得开关管S1的开关状态为：

(11)

4.2.3 Buck-Boost变换器控制策略

取电感电流误差X1、电压误差X2作为受控状态变量：

[x1,x2]=[IL2-ref-IL2，Udc-ref-Udc]

(12)

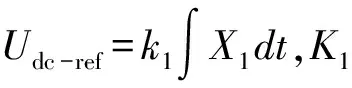
(13)

结合式(2)、(3)和式(13)可知：

(14)

5 仿真分析

通过MATLAB/simulink搭建HESS模型进行仿真实验。基本参数见表2。由于电动汽车大多使用于城市道路，同时为了减少仿真运行时间，故选择新欧洲循环工况NEDC(The New European Driving Cycle)的一部分进行仿真实验。本文只分析HESS部分，对负载部分不做研究，因此为了简化分析，负载选用阻值随功率变化起而变化的可变电阻负载；电动汽车刹车减速时，用一个电压源来代替由电驱动状态改为发电状态的电机。在NEDC下，车辆的速度见图5。

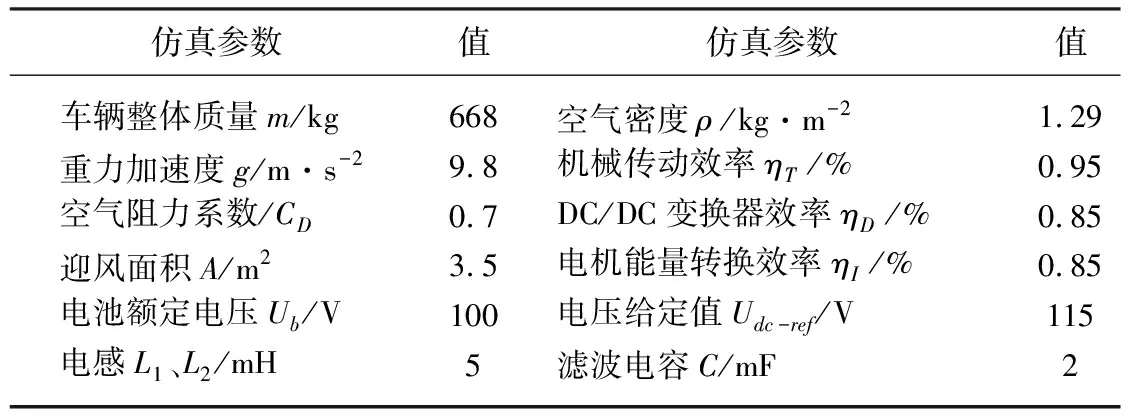
表2 电动汽车仿真参数

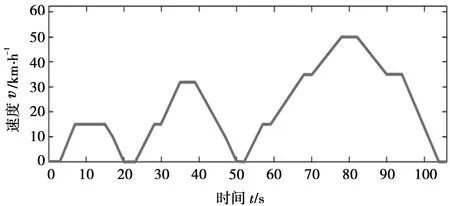
图5 NEDC工况部分车速波形

图5中，车辆运行工况总时长为106 s，行驶过程分为三个部分：0～20 s为低速行驶状态；20～50 s为中速行驶状态；50～106 s为加速至高速行驶状态，基本包含了车辆的不同运行状态。结合式(7)，求得车辆的需求功率，如图6所示。图6中，由于在低速行驶状态下，车速只有小幅度的变化，因此车辆的需求功率变化幅度较小。但当车辆在从静止加速到高速状态时，由于车辆的加速度以及加速时间的不同，车辆的需求功率变化也更加复杂。因此可以更好地检验控制系统在复杂环境下的有效性。

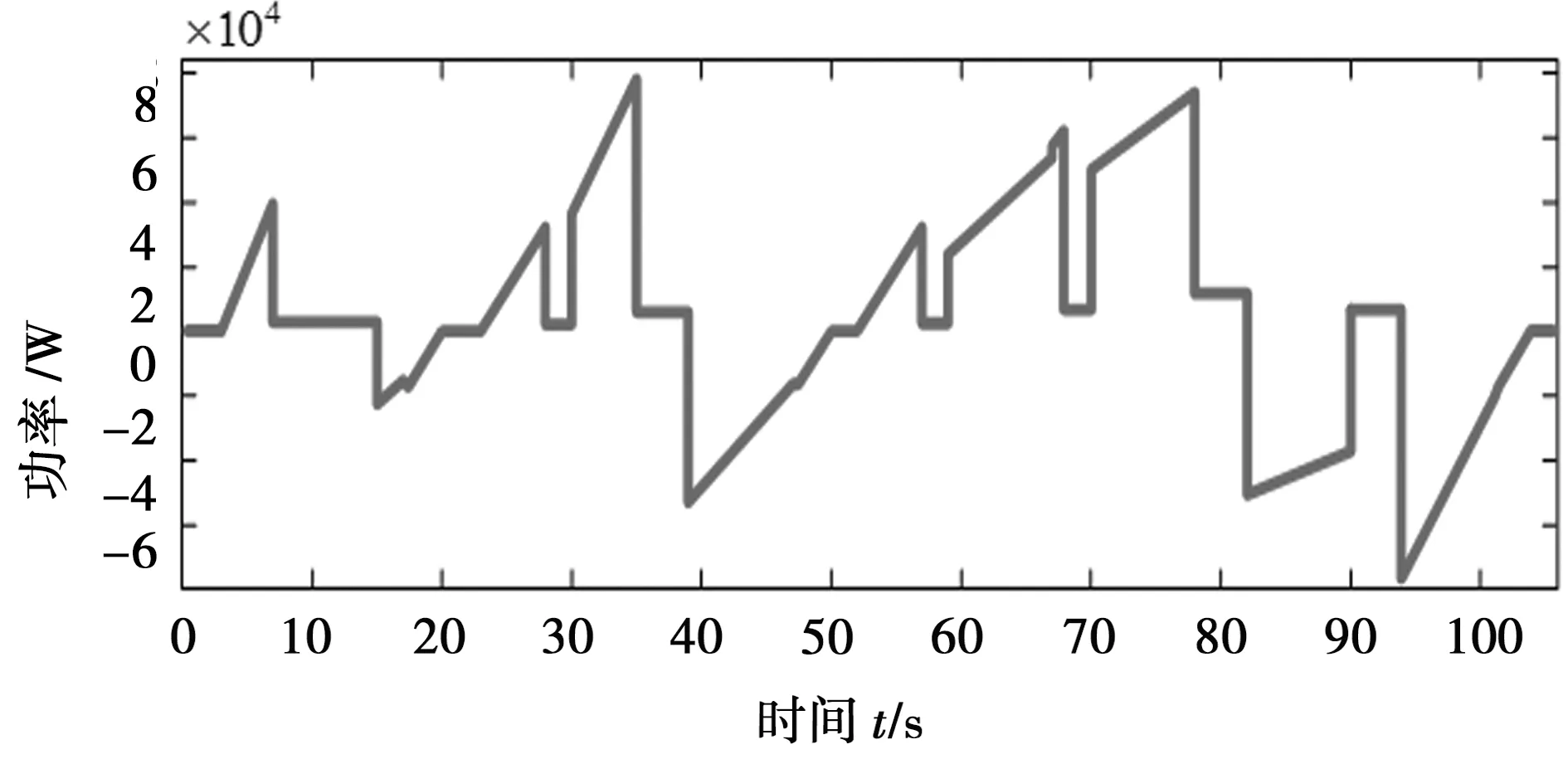
图6 电机需求功率波形

在图5和图6的运行环境下运行仿真系统，从而验证控制系统的有效性。

图7为整个仿真时间内直流母线电压的波形变化曲线。由图7可知，母线电压值在整个仿真时间内总体维持在设定值，将母线电压变化曲线放大，图中曲线表明，母线电压上下浮动不超过1 V。

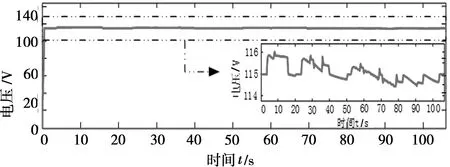
图7 直流母线电压波形

图8为复合电源电流波形变化曲线。当需求功率较小时，仅蓄电池介入工作为电机供电；当需求功率较大时，在蓄电池持续工作的同时超级电容组也介入工作，蓄电池与超级电容同时为电机供电[10]。此模式避免了蓄电池频繁地过电流充放电。

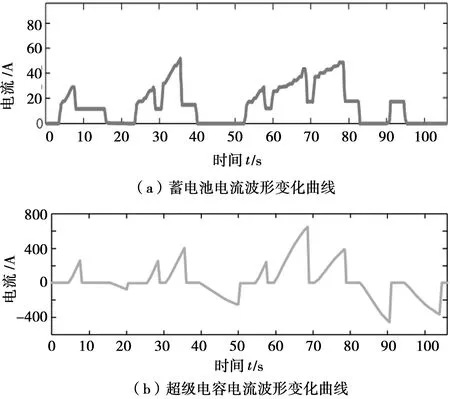
图8 HESS电流波形

如图9所示，由于超级电容能量密度低，并且提供瞬时大功率，因此荷电状态下降明显；蓄电池能量密度高，同时有超级电容提供瞬时大功率，因此荷电状态变化比较平缓。当车辆刹车减速时，此时由超级电容回收制动所产生的电能，当超级电容荷电状态达到上限时，超级电容停止回收能量，能耗电阻消耗制动能量，避免了因过充而损坏超级电容。

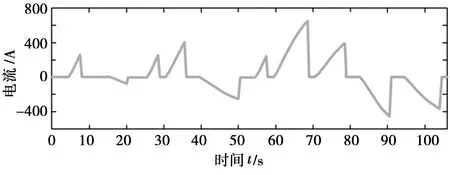
图9 复合电源SOC变化曲线

6 结 语

本文详细分析了HESS的四种工作模式，并提出一种基于车辆需求功率变化的模糊控制分配策略和新型趋近律控制方法相结合的混合控制策略。通过仿真实验，得出以下结论：

(1)相较于蓄电池单独工作，超级电容的加入避免了大电流对蓄电池造成损坏，高效回收制动能量，从而延长电池的使用寿命，增强车辆的续航能力。

(2)模糊控制方法能够较好地解决蓄电池与超级电容之间的功率分配问题：蓄电池提供相对较小功率，瞬时大功率则由超级电容组提供。

(3)基于新型趋近律的控制策略可以很好地控制复合电源的功率输出，维持母线电压的稳定。

通过仿真实验，本文所提出的模糊-新型趋近律滑模控制的控制策略的可行性和有效性得到了验证，但还有许多新的问题需要解决，例如实际运用过程中，各个元器件和运行环境中的各种扰动对控制策略都会有或多或少的影响，因此，未来还需要在实际应用中不断积累和完善。