基于目标运动建模的声呐探测性能分析方法
王飞 丁烽
(第七一五研究所,杭州,310023)
如何在海上作战中寻找并打击潜艇,赢得主动,一直是水面舰艇不断探索和研究的课题。反潜作战首要任务是发现对方潜艇,由于潜艇具有良好的水下隐蔽性和较强的水声对抗能力,且现代潜艇朝高速、深潜和低噪声方向发展,使搜索发现潜艇愈加困难和复杂[1]。因此,水面舰艇编队在实施反潜行动之前,应对搜索区域中目标的运动特征及声呐探测性能进行全面的认识,以便根据水声环境和搜潜任务制定相应的战术决策。
从战术和作战的角度来看,评估声呐性能的一个重要指标是声呐作用距离,这与具体海洋环境、目标分布和接收深度密切相关。同一声呐设备在不同海洋环境的探测性能差异巨大。对于水面舰艇声呐,声呐设备应放置在最有利于探测水下目标的区域。至于水下目标潜艇,要让自己处于敌舰探测性能最差的区域,最大程度降低被发现的可能性[2]。因此研究声呐在复杂环境中执行作战任务、水下目标位置变化时的声呐探测性能等具有重要意义。本文以水面舰艇编队协同搜潜为研究背景,对声呐设备的探测性能进行研究。
1 声呐探测性能模型
对于水面舰艇编队搜潜而言,在不同的海域进行搜潜任务时由于海洋环境不同声呐探测性能也就不相同。Carlo M Ferla在研究深海声呐最佳工作深度的过程中发现,当目标深度未知时,通过统计声源在不同深度的声场概率分布,可得到声呐的最佳工作深度[3]。基于这一思想,本文估算了声呐在同一深度不同海洋区域内的探测性能,分析声呐的最佳工作区域。在面对复杂多变的海洋环境时,我们构建了一个与目标位置有关、能够描述整个搜索区域内声呐探测性能优劣的模型,便于更好地捕捉搜潜任务中的复杂和动态的声学特征。
1.1 主被动声呐方程
海洋是一个复杂多变的环境,水声信道复杂。将声呐装置放置于水下一定深度,组成单基地声呐。发射换能器向目标发射脉冲信号,接收水听器接收目标回波,最后处理目标回波完成对目标的检测和定位工作[4,5]。此时主动声呐方程可以表示为
式中,SL为声源级,NL为噪声级,DI为指向性指数,TL为传播损失,TS为目标强度,RL为混响级。
在感兴趣的地理区域若干个均匀分布的栅格进行信噪比SNR的计算,如图 1左图中标示出的各个点。在每个栅格点沿着水平距离划分网格,设目标位于某网格点,利用射线模型计算传播损失TL或2TL。合理设置式(1)等号右边的各个参数,可以估计目标在该网格点的信噪比SNR。
图 1是整个搜索区域内SNR的计算过程,左侧图显示了最开始的典型实例栅格,所示的区域内海洋环境复杂,声呐探测性能差异大。根据这些地理位置,SNR是一个有关栅格位置(x,y)、距离r和方位角θ的函数。右侧的图表示在地理区域上重复计算,排列成和区域位置相关的SNR(x,y,r,θ)。
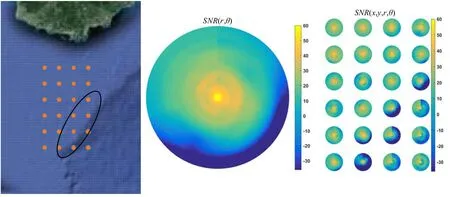
图1 信噪比重复计算过程
1.2 声呐探测性能计算模型
当声呐方程的各参数确定后,即可得到确切声呐对目标的探测距离。但是在实际情况中,声呐的探测范围受到自身性能、目标状况、环境条件、主观因素等诸多因素的影响,使得声呐探测性能的估计具有一定的不确定性,从而导致声呐探测范围存在不确定性,此时声呐探测距离不再是某一固定值,而是满足一定分布的概率值。本文使用概率函数描述在声呐探测范围内声呐探测性能存在的不确定性,建立基于声呐探测概率求和的声呐探测性能计算模型。
检测模型可将声呐方程中的SNR转换成声呐性能度量检测概率Pd。检测模型定义为
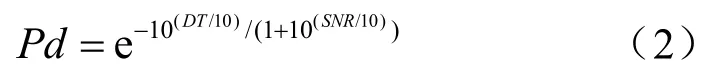
式中,DT为检测阈,其接收机工作曲线(ROC)如图2所示。
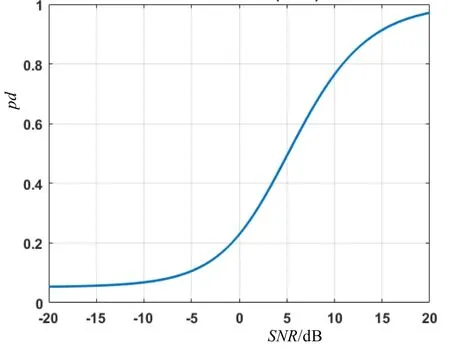
图2 ROC检测模型
该曲线描绘了在目标存在的情况下进行检测的概率与信噪比的关系。每个SNR值都被映射为条件检测概率,如图3所示,SNR越大,画面越亮,表示该区域探测到目标的概率越大。
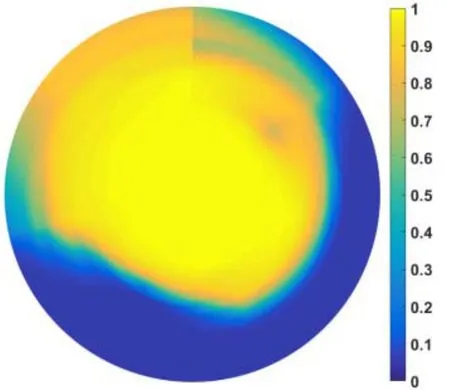
图3 条件检测概率P(D|T)=Pd
前面的讨论都是在假设目标在声呐探测范围内的情况下进行的,在目标分布信息未知的情况下,前面的理论是不适用的[6]。为了得到水面舰艇搜索范围内的声呐探测性能,假设水下目标在声呐探测范围内服从一定的概率密度分布,如均匀分布、正态分布,然后将声呐探测性能看作是目标在某个位置时关于目标所在极坐标位置(r,θ)的函数。
假设目标在声呐探测范围内服从均匀分布的概率密度为P(T),如图4所示。计算声呐在每个目标位置的联合检测概率,并将这些概率值相加,得到栅格网络中每个网格点的声呐探测性能估计值。
图4 目标均匀分布时的概率密度P(T)
用式(3)说明上述的整个过程:
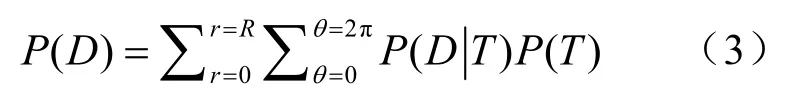
之后利用插值方法将概率值P(D)扩展到整个感兴趣区域,便可得到声呐探测性能,如图5所示。图中,使用从蓝色到红色的色标表示从0到1的声呐探测性能差异。探测性能表示指定的目标接收器深度下,在给定范围内声呐设备检测到目标的概率。这可以帮助任务指挥官更好地考虑搜索资源分配和移动决策。图1左图所示区域标示的地方有一道明显的海坡,海洋环境复杂,该区域的声呐探测性能相对于其他区域较差,图5中对应区域也表现出相同的声呐探测性能。后文仿真中对声呐探测性能的分析都在图1所示的区域内进行。
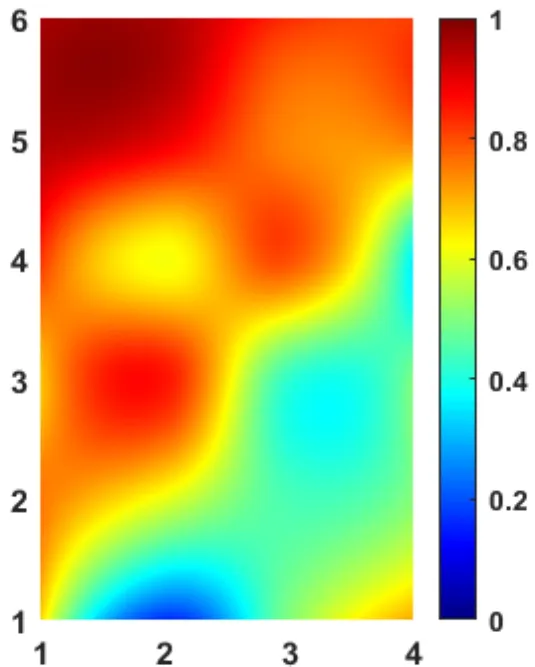
图5 搜索区域内声呐探测性能
2 水下目标运动建模
2.1 用维纳过程推导Fokker-Planck方程
本文借鉴文献[7]、[8]中的运动目标建模思想,基于FP方程推导空间滤波器,也称作FP滤波器,研究目标运动条件下的目标存在概率更新规则。
我们利用FP方程和布朗运动对目标漂移和扩散过程进行建模,首先针对一维情况,此时目标运动建模为维纳过程,定义为
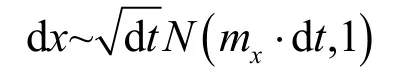
式中,dt是时间增量,目标在时间dt上的移动距离dx是一个随机过程,N(mx·dt, 1)代表均值为mx·dt、方差为1的正态分布。
假设目标在时刻t位于位置x的概率密度函数为ρ(x,t),随着时间变化关系为
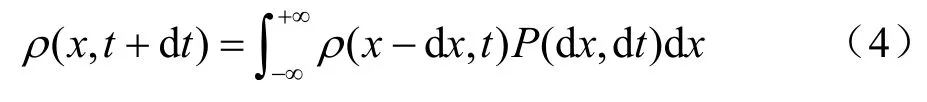
式中,P(dx,dt)表示目标在时间dt内移动dx的概率。泰勒级数展开后得

一般dt很小,将式(5)简化为
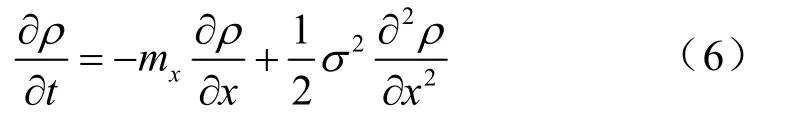
式(6)是一维FP方程,将二维FP过程定义为

维纳过程扩展到二维情况,同理可得

式中,-mx和-my分别表示x、y方向上目标运动的漂移系数,分别表示x、y方向上目标运动的扩散系数。
利用有限差分法来求解式(7)中的FP方程。首先定义下列离散变量:

式中,Δx和Δy确定了x-y平面内划分网格的大小。nx和ny分别为x和y方向上离散的空间网格数目。离散的单位时间增量Δt,任务总时间为nt。用有限差分法解式(7),得
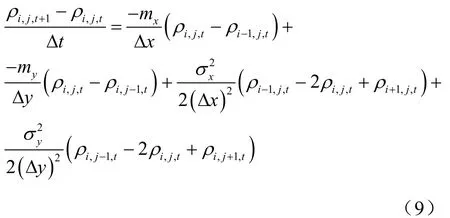
假设t单位时刻,网格i、j处的目标概率密度分布ρi,j,t已知,利用式(9)可得t+1单位时刻ρi,j,t+1的分布。当假设Δt=1 s时,式(9)可简化为
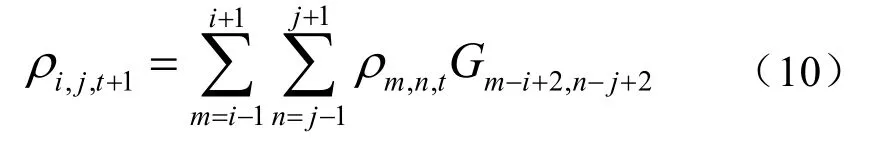
式中,空间滤波器G的表达式为
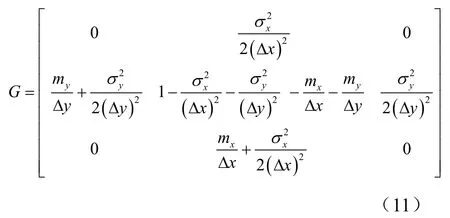
2.2 目标适应性运动
在足够大的搜索区域内,由于环境复杂性、设备和信号处理方式的不确定性,声呐设备的探测性能是不确定的。因此,可以合理假设,该区域声呐设备的不同声学性能将影响目标的分布规律。我们假设敌方水下目标已知晓搜索编队在搜索区域内的探测性能图,为了在作战过程中逃避搜索和攻击,目标会选择搜索平台探测性能“差”的地方移动。为了更好地了解真实的目标运动规律,将目标的这种适应性选择移动加入到目标的运动约束中[9],如图6所示。Hmap图中的值表示目标移动到该区域的可能性。

图6 适应性移动图
将式(10)更新后的水下目标概率密度函数和目标的适应性移动结合,得到

回归到本文讨论的概率下的目标运动问题,文中给出的ρi,j,t表示目标在时刻t存在于网格点(x,y) = (iΔx,jΔy)的概率,即PT(x,y,t) =ρi,j,t。
3 仿真实现与结果分析
水下目标潜艇位置和运动存在的不确定性,决定了对潜艇的搜索是一件随机事件。当用统计方法描述水下潜艇的这种不确定性时,需要事先假设水下潜艇位置和运动的散布服从某种规律,而实际的潜艇运动规律与水面舰艇编队执行的搜潜任务和目标作战环境密切相关[10,11]。
为了充分掌握水面舰艇在搜潜任务中的探测性能,我们通过一个搜潜场景来评估本文提出方法。潜艇的运动规律假设与水面舰艇编队执行的搜潜任务有关,结合区域搜潜任务场景下目标运动的情况对声呐探测性能进行分析。由于执行区域搜索任务时不能确定在指定海域内是否存在潜艇目标,或者无法提供有关目标潜艇位置的具体信息。因此当该区域存在潜艇时,假设其初始位置在该搜索区域的二维均匀分布是合理的,在假设初始位置是均匀分布的条件下,先对复杂环境中目标适应性运动进行建模,之后分析目标运动后分布不均匀时的声呐探测性能。
根据搜索平台的搜索能力将搜索区域划分若干个网格,每个网格大小为500 m×500 m。式(9)中,Δt=1 min。t=0 min时,侦查兵力在某区域探测到水下目标,但是不知道具体位置。假设在区域内均匀分布,在附近驻泊的水面舰艇编队接到命令后,经过一段时间的准备在可疑区域内执行搜索任务。在这段时间内,目标不可能停留在原处,在自身未暴露的情况下,目标会在搜索区域内运动。本文在假设目标向外做扩散运动是均匀的基础上,对目标适应性运动进行仿真。先使用式(10)对目标在每个网格中的存在概率进行更新,目标只存在扩散运动,其中mx=my=0 m/s,σx=σy=16 m2/s。在每个更新时刻结束后使用式(12)对目标运动进行约束。目标在t=0~300 min时间内的概率密度变化情况如图7所示。从图中可以看出,目标不再呈现均匀分布。图中红圈表示进行径向信噪比测量的圆点。从t=300 min时的图中可以看出,目标会适应性移动到搜索平台声呐性能“差”的区域。

图7 区域搜潜任务中目标概率密度变化情况
在前面章节中,分析了水下目标均匀分布时的声呐探测性能,目标均匀分布这种假设是不够全面和合理的。图7给出了由于目标适应性移动造成的不规则运动目标分布情况。为了更好地描述水面舰艇在执行不同搜潜任务时的声呐探测性能的变化情况,需要对不规则运动下的目标分布时的声呐探测性能进行分析。通过将均匀分布时的概率密度替换成目标适应性运动后的概率密度即P(T) =PT(i,j,t),可得到目标分布不均匀时的声呐探测性能。
图8给出了图7中各个时刻的目标位置分布情况对应的声呐探测性能。从图中可以看出,当t=0 min时的声呐探测性能和假设的目标均匀分布时不一样,这是因为前者假设目标在整个搜索区域范围内均匀分布,后者是在声呐探测范围内均匀分布,这两者的声呐探测性能数值成倍数关系,其意义相同。另外随着目标的移动,在目标概率密度大的区域声呐探测性能明显变好。但从图8中t=300 min时可以看出左下方的声呐探测性能差,这是因为此区域环境导致声呐设备的声学性能差,即使目标在此区域,都有很大的可能探测不到。
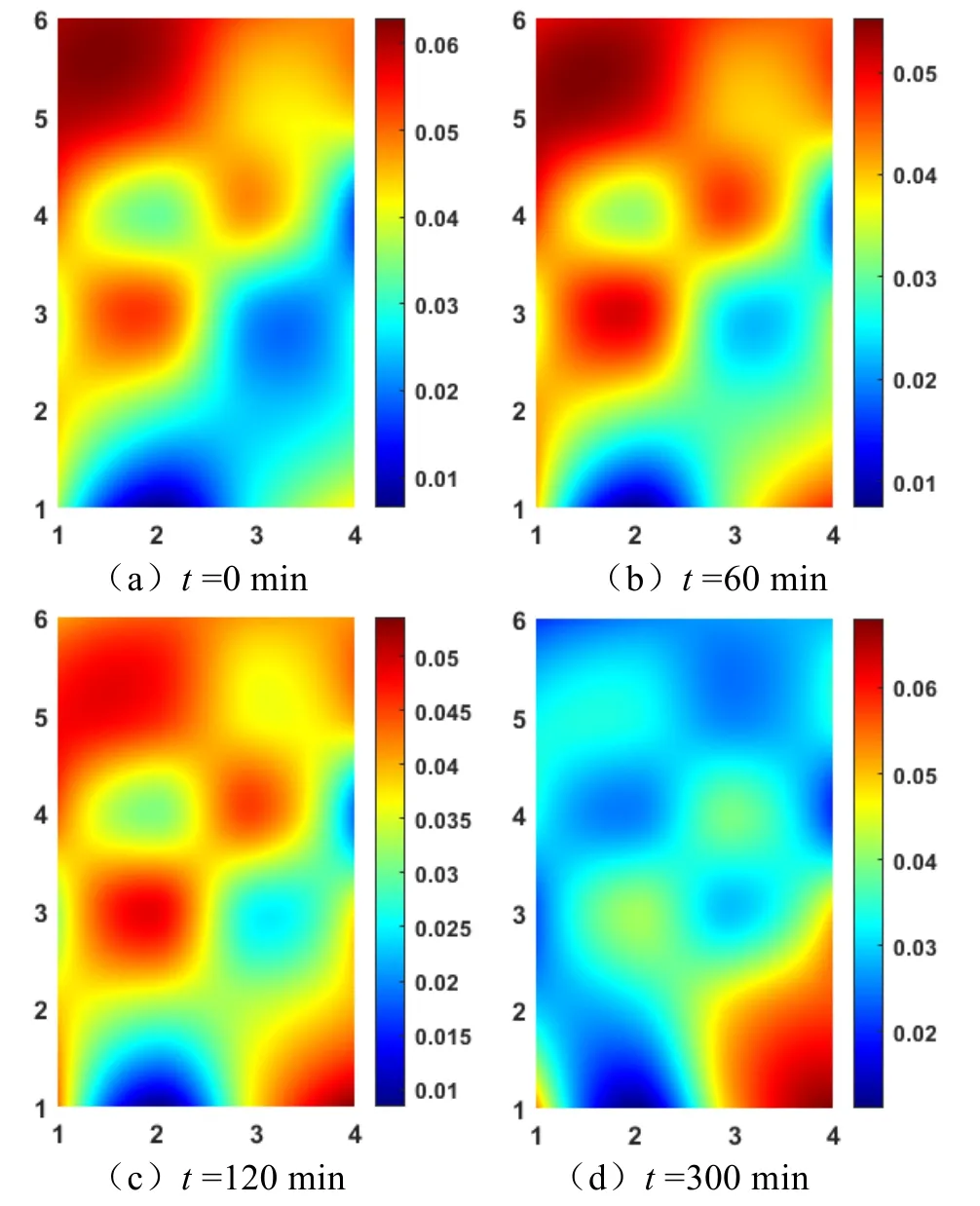
图8 区域搜潜任务中声呐探测性能变化情况
4 结论
本文为分析搜潜作战过程中声呐探测性能提供一种参考方法,将复杂海洋环境、目标运动模型与声呐检测性能紧密结合在一起,实现了在搜潜任务中水面舰艇编队对搜索区域内声呐探测性能的描述。利用FP空间滤波器和布朗运动对水下目标运动进行建模,使得目标运动规律和实际战术行为相吻合。整个工作区域内的探测性能为作战指挥员选择声呐最佳工作区域提供了理论支持,模型能够更好地描述声呐的真实工作情况。

