基于PSO算法的地铁智能调线调坡系统开发与研究
刘 欣
(广州地铁设计研究院股份有限公司, 广东 广州 510010)
0 引言
调线调坡是城市轨道交通建设过程中必不可少的一个环节,目的是消除施工偏差,使线路合理平顺,满足限界要求。同时,调线调坡工作也为后续施工阶段铺轨、设备安装等提供设计依据。
目前,国内学者针对调线调坡方法开展了大量研究,但大部分文献仅是针对传统人工调线调坡进行分析和讨论。李家稳等[1]提出“双边线形约束”优化算法理论,并利用距离法和面积法求解目标函数,有效解决了侵限问题。郭俊义[2]总结了盾构区间施工阶段引起线路偏差的原因,介绍了隧道内结构、车辆、接触网、轨道等专业的限界富余量,总结了调线调坡技术的要点和步骤。罗江胜等[3]将发生被动调线调坡的原因分类为测量原因、设计原因、施工原因、道床病害治理原因等,并提出了相应的对策。李建斌[4]详细介绍了调线调坡工作流程,即断面测量、限界检查、数据分析、调线及调坡设计,并总结了调线调坡技术的设计要点。吴爽[5]基于AutoCAD程序开发了调线调坡设计系统,提出将测量基准线调整至结构底板处可减少现场测量工作量和提高设计效率。赵强[6]、黄小纯[7]、余喜红[8]结合工程实例讲解了调线调坡的设计流程,对设计中遇到的问题给出了解决思路和建议。胡雷等[9]、Chen等[10]采用点云技术构建圆形断面隧道三维模型,并分别采用深度神经网络、遗传算法进行调线调坡计算,建立智能设计系统。
传统的调线调坡工作是根据线路断面测量数据梳理侵限部位、侵限里程,然后人工调整线路平、纵断面; 调整后重新测量、分析线路侵限情况,继续调整设计线路各参数,直至达到满意的调线调坡效果。整个过程需要反复调试和判断,繁琐且容易出现错漏,工作效率低下,不同的设计人员会调出不同的方案; 且针对调线调坡成果,没有有效的评价指标,无法衡量调线调坡方案的优劣。
由上述研究成果可知,目前国内在智能调线调坡技术研究方面,仅胡雷等[9]、Chen等[10]取得了一些成果,但成果中局限于圆形断面隧道,且无相关的线路合规性检测。本文提出了基于粒子群算法的智能调线调坡一体化技术,构建了求解稳定的智能调线调坡模型,创新性地建立了含断面侵限权重、侵限容忍值和线路合规性惩罚项的调线调坡目标函数,可得到适应度最优的调线调坡方案,并开发了适用于矩形、马蹄形、圆形等多种隧道断面类型的地铁智能调线调坡设计系统,极大地降低了人力成本。
1 粒子群优化算法
粒子群优化算法(particle swarm optimization,PSO)是由Kennedy和Eberhart于1995年提出的一种实现简单、搜索高效、收敛快速的群体智能算法。在粒子群算法模型中,每一个粒子的自身状态都由1组位置和速度向量描述,分别表示问题的可行解和其在搜索空间中的运动方向。粒子通过不断地学习其所发现的群体最优解和邻居最优解,实现全局最优搜索[11-13]。以二维平面为例,粒子i的当前位置和速度分别为Ci(t)和Vi(t),历史最优位置为pbest,i(t),整个种群粒子的历史最优位置为gbest,i(t)。那么,粒子i下一时刻的速度Vi(t+1)由当前速度Vi(t)、个体历史最优位置pbest,i(t)和种群历史最优位置gbest,i(t)共同组成,如图1所示。按照速度Vi(t+1)更新位置为Ci(t+1)后,再比较个体和种群的历史最优位置,反复迭代,直至达到终止条件。
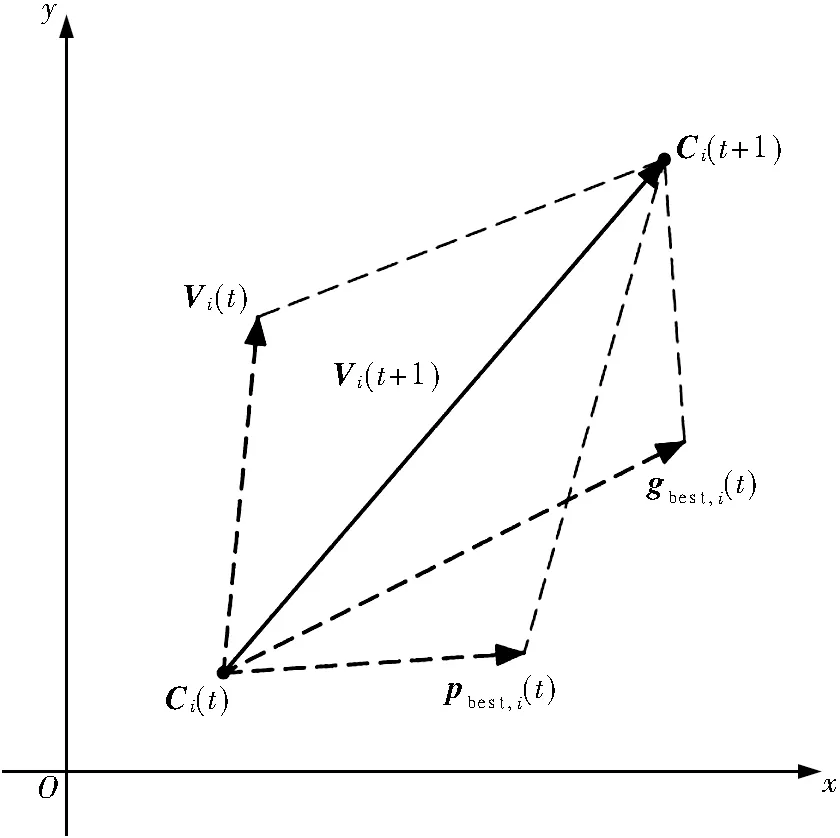
图1 粒子移动示意图Fig. 1 Image of particle movement
Vi+1(t+1)=wVi(t)+c1r1[pbest,i(t)-Ci(t)]+c2r2[gbest,i(t)-
Ci(t)]。
(1)
Ci+1(t+1)=Ci(t)+Vi(t+1)。
(2)
式(1)—(2)中:w为惯性权重,代表当前速度对下一时刻速度的影响;c1、c2为加速因子;r1、r2为[0,1]的随机数。
粒子群算法概念清晰、稳定性好,适用于求解约束条件多、目标明确的最优解问题。轨道交通领域内,粒子群算法在列车运行调度[14]、客流预测[15]、纵断面节能优化[16]等方面均有研究运用。
2 智能调线调坡模型的建立
将粒子群算法与调线调坡设计相结合,建立合理可靠的数学优化模型,能高效、智能地进行调线调坡设计。分别从设计变量、约束条件、目标函数3个方面进行分析,建立平面调线模型和纵断面调坡模型。
在给定线路起终点的情况下,可利用平、纵断面设计的线路基本要素来确定线路方程。本文采用平面交点坐标(x,y)、曲线半径R作为平面设计变量。平面缓和曲线长度l1和l2在地铁线路设计中一般会对应曲线半径和列车运行速度选配固定值,不设为设计变量。故线路平面方程表示为T1(xio,yio,Rio),io表示平面交点编号。将变坡点高程h、里程k作为纵断面设计变量,线路纵断面方程表示为T2(hjo,kjo),jo表示变坡点编号。通过修改以上设计变量,可对任意侵限段线路的平、纵断面进行调整。
2.1 平面调线模型
2.1.1 设计变量
在平面调线模型中,不改变纵断面设计变量的数值。线路方程可写成T1(x,y,R)。[x,y,R]表示所有交点的平面坐标与对应的曲线半径组成的矩阵。
2.1.2 约束条件
约束条件主要按合规性要求设置,一般情况下,不可突破《地铁设计规范》[17]相关条款规定。
2.1.2.1 最小曲线半径
平面调整后的曲线半径,需大于等于根据车辆类型、地形条件、运行速度、环境要求等综合因素确定的线路平面最小曲线半径。例如: A型车正线一般地段最小曲线半径为350 m,困难地段最小曲线半径为300 m; B型车正线一般地段最小曲线半径为300 m,困难地段最小曲线半径为250 m。以困难情况下规定的最小曲线半径为约束限值,约束函数表示为
φ1(x,y,R)=Rio-Rmin≥0。
(3)
式中:Rio为第io交点对应的曲线半径,m;Rmin为困难情况下规定的最小半径,m。
2.1.2.2 圆曲线最小长度
对于线路的圆曲线长度lc,A型车不宜小于25 m,B型车不宜小于20 m,困难情况下不小于1节车辆全轴距。以圆曲线长度不小于1节车辆全轴距为约束限值,约束函数表示为
(4)
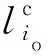
2.1.2.3 平面曲线间夹直线最小长度
对于相邻曲线间的直线段长度lH,A型车不宜小于25 m,B型车不宜小于20 m,困难条件下不小于车辆全轴距。以平面曲线间夹直线长度不小于车辆全轴距为约束限值,约束函数表示为
(5)

2.1.3 目标函数
根据常用的限界测量方式,在某一里程l,对于矩形、马蹄形、圆形等类型的隧道,断面测量会对左上、左中1、左中2、左下、右上、右中1、右中2、右下、顶、底等10个固定断面位置进行量测,以描述该里程成型隧道的形状。以轨面线中点为原点O,线路中心线为y轴,过原点水平线为x轴,建立坐标系,如图2所示。左、右侧测量点与y轴的距离为eH。设计限界考虑了隧道加宽值和偏移量后,对应点与y轴的理论距离为e′H。当δ=eH-e′H<0时,判断左、右侧隧道为侵限。
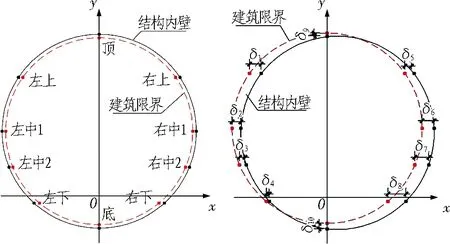
(a) 圆形隧道断面
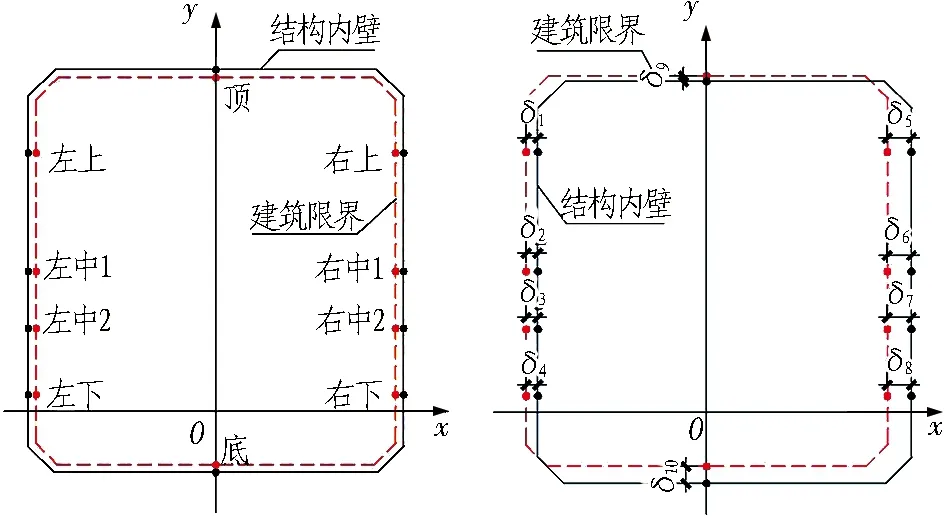
(b) 矩形隧道断面

(c) 马蹄形隧道断面图2 隧道断面侵限示意图Fig. 2 Image of limit invasion of tunnel section
在隧道断面内不同的位置出现侵限,需针对性设计和调整对应位置的隧道设备敷设安装方式,以消除或减轻侵限影响,不同的专业设备处理代价也不尽相同。故建立平面调线目标函数时,有目的地引入权重对左右侧8个测量点进行针对性赋值,调线设计优先解决侵限程度较大、工程要求较高的断面侵限位置。在平面限界检查中,测量断面对应里程为l,将该断面的平面侵限值累加,得到如下公式:
式中:αiq为隧道断面横向侵限权重因子,αiq∈[1,10]。n为测量断面的左、右侧测量点数量,n=8。sgn(δ)为阶跃函数,当δ>0时,sgn(δ)=1; 当δ<0时,sgn(δ)=-1; 当δ=0时,sgn(δ)=0。由此可知,f1≤0。
测量断面内若产生严重侵限点,可能导致处理难度增加,甚至需要进行土建改造。为避免此类情况,目标函数增加一项惩罚项,设置横向侵限容忍值,当δ小于容忍值时,惩罚项生效,额外附加目标函数值:
(7)
式中:κiq为容忍值惩罚项因子,κiq∈[0,10];n为测量断面的左、右侧测量点数量,n=8;θ1为横向侵限容忍值,θ1≤0 mm。由此可知,g1≤0。
对某一组线路要素确定的线路,需进行合规性检查。当调整线路满足规范困难条件的限值,但不符合一般情况的要求时,将可能降低行车功能和增加运营维保难度,故设置另一小于0的惩罚项(见式(8)),不满足规范一般情况要求时激活。
(8)
式中:η为合规性惩罚项因子,η∈[0,10];aic为平面内不满足规范一般情况规定的项目值;aic,line,aic,lim分别为规范对应的一般情况规定值和困难情况规定值;N为平面线路不满足一般情况要求的项目数量;D1为不考虑偏差的情况下横向建筑限界到结构内壁的理论距离(mm),作为合规性惩罚项的基数,D1越大,p1越小。
本文将平面调线模型的目标函数设为搜索所有测量断面侵限值总和的最大值,则调线模型可表示为
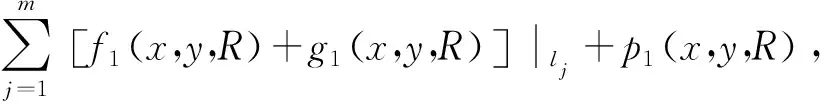
φ1(x,y,R)≥0,φ2(x,y,R)≥0,φ3(x,y,R)≥0。
(9)
式中:m为测量断面的数量;lj表示第j个测量断面所对应的里程,m。
2.2 纵断面调坡模型
2.2.1 设计变量
在纵断面调坡模型中,不改变平面设计变量的数值,则线路方程可写成T2(h,k)。[h,k]表示线路各变坡点的高程和对应里程组成的矩阵。
2.2.2 纵断面约束条件
2.2.2.1 最大、最小坡度
坡度是影响地铁纵断面设计的重要技术标准。地铁正线最大坡度不宜大于30‰,困难地段不超过35‰;隧道内和路堑地段正线最小坡度不宜小于3‰,困难地段在保证排水的条件下可采用2‰。以困难情况下的坡度规定为约束限值,约束函数表示为
ψ1(h,k)=(ijo-imax)·(ijo-imin)≤0。
(10)
式中:ijo为第jo变坡点对应的坡度,‰;imax、imin分别为困难地段规定的最大、最小坡度,‰。
2.2.2.2 最小坡段长度
线路坡段长度不宜小于预期列车长度,且相邻竖曲线间夹直线长度不小于50 m。以竖曲线间夹直线长度lV不小于50 m为约束限值,约束函数表示为
(11)
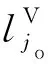
2.2.2.3 最低点位置
区段最低点一般都设置有联络通道兼作废水泵房,一个区间可能会出现多个区段最低点。调线调坡往往对单线进行,另一条隧道一般都满足原设计线路要求。故为保证排水顺畅,不对调坡区段的最低点进行较大的调整。因此,要求调整后区段最低点的位置里程应在原设计线路最低点里程前后10 m范围内。约束函数表示为
ψ3(h,k)=10-|Zk-Z′k|≥0。
(12)
式中Z′k、Zk分别为区间内调坡前后第k个最低点的里程,m。
2.2.3 目标函数
在图2中,顶、底测量点与x轴的距离为ev,设计限界对应点与x轴的理论距离为ev′。当δ=ev-ev′<0时,判断隧道顶、底面为侵限。
建立纵断面调坡目标函数时,同样对顶、底2个测量点设置不同权重。已知测量断面对应里程为l,将该断面的顶、底面侵限值相加,得
(13)
式中:α9,α10为隧道断面竖向侵限权重因子,取值范围为[1,10]。由此可知,f2≤0。
设惩罚项的竖向侵限容忍值为θ2(θ2≤0),当δ超过容忍值时,惩罚项将大幅影响目标函数值,与式(7)类似,g2≤0。
g2(h,k)|l=
(14)
对各项纵断面参数进行合规性检查。设置纵断面参数合规性惩罚项(见式(15)),当某一参数不符合规范一般情况要求时生效。
(15)
式中:η为合规性惩罚项因子,与式(8)一致;bjc为纵断面不满足规范一般情况规定的项目值;bjc,line,bjc,lim分别为规范对应的一般情况规定值和困难情况规定值;M为纵断面线路不满足一般情况要求的项目数量;D2为竖向建筑限界到结构内壁的理论距离,m。
综上所得,线路调坡模型如下:
ψ1(h,k)≤0,ψ2(h,k)≥0,ψ3(h,k)≤0。
(16)
2.3 优化算法计算策略
本文将粒子群算法应用至平、纵断面调线调坡模型中,转化为求解多约束的最大化问题,粒子群优化算法步骤如下。
1)步骤1: 种群初始化。
①平面调线和纵断面调坡为2个相对独立的计算模块,系统推荐采用先纵断面后平面的优化策略。在纵断面调坡模块计算时,先取出调坡的线路范围,粒子初始种群为该段范围的纵断面线路设计参数组成的要素矩阵[h,k];在平面调线模块计算时,先取出调线的线路范围,粒子初始种群为该段范围的平面设计参数组成的要素矩阵[x,y,R]。
②每个粒子位置向量Ck为每一组线路参数设计变量的值。
③每个粒子速度向量Vk的惯性权重值取0.8~1.2之间的随机数。
④用目标函数评价所有的粒子,在满足规范的条件下,以减少总的侵限值为目标,具体评价目标函数平面调线模块采用式(9),纵断面调坡模块采用式(16)。
⑤将初始种群各个粒子的评价值作为各自个体的历史最优解pbest,k,并比选出初始评价值中的种群最优解gbest,k。
2)步骤2: 按以下步骤重复计算,直到满足计算终止条件,即已达到收敛精度或最大迭代次数。
①对每一个粒子按照式(1)与式(2)更新位置信息,超过取值范围时按边界取值。
②用评价函数评价所有的粒子。
③若每个粒子的当前评价值优于其历史最优评价值,则记该粒子的当前评价值为该粒子的历史个体最优评价值,当前位置为该粒子历史个体最优位置pbest; 同时,寻找总群体中的历史最优解,若粒子当前评价值仍优于总群体历史最优评价值,则更新总群体历史最优位置gbest。
④当总群体历史最优位置gbest在连续100代未更新或迭代次数达到10 000时,搜索结束,输出总群体历史最优解信息。
根据上述粒子群优化算法的求解策略,开发出一套针对不同工法的地铁智能调线调坡设计系统,充分发挥智能算法的高效性和准确性。此外,系统内置了坐标转换功能,将测量值转换为绝对坐标,并针对圆形、马蹄形隧道进行断面拟合,无需在每次调整方案后再进行现场复测核对,自身就可形成设计计算的闭环。系统在断面拟合时将顶点、左上(右上)、左中1(右中1)3点坐标进行圆曲线插值,形成一段圆弧,用同样方法分别对左中1(右中1)、左中2(右中2)、左下(右下)3点坐标,左下、底点、右下3点坐标进行圆曲线插值。圆形、马蹄形隧道整体断面由5段圆弧构成。在调线调坡过程中,线路的调整将导致同一位置线路中心线的法平面发生变化,新线路方案的法平面与原测量断面不重合,但此类变化是微小的,产生的误差在实际工程中是可以接受的。故系统中仍利用原测点数据拟合的断面进行线路调线调坡侵限计算。当系统调线调坡设计结束后,再次采用新的设计线路对成型隧道进行一次现场断面测量,复核侵限情况。
3 工程案例分析
本节以长沙地铁4号线某区间的右线调线调坡设计为例,对比地铁智能调线调坡设计系统与人工调线调坡的设计成果,验证智能系统的有效性。
3.1 工程概况及侵限分析
长沙地铁4号线某区间右线长1 195 m,采用盾构法施工,区间包括3组平面曲线,曲线半径均为350 m。区间隧道纵断面按V坡节能设计,从小里程车站出站后分别以25‰(坡长290 m)、5‰(坡长270 m)下坡,接7.0‰(坡长580 m)坡度上坡进入大里程车站,最大纵坡为25‰。盾构管片内径为5.4 m,限界圆直径为5.2 m。
该区间右线隧道由于施工控制质量较低,断面测量数据显示隧道内多处侵限。通过加密测量发现: 平面第2组曲线范围内,存在69处左侧测量点侵限,即成型隧道向右侧偏移,最大侵限值288 mm,部分区段已无法满足疏散平台的最小宽度要求,需进行调线设计; 平面第3组曲线范围内,存在65处右侧测量点侵限,最大侵限值142 mm,经限界专业核算,不影响隧道右侧设备的安装和使用。调线前隧道横向侵限情况如图3所示,调坡前隧道竖向侵限情况如图4所示。隧道区间共有107处底部侵限点,无顶部侵限。底部最大侵限值为71 mm,隧道轴线较设计线路上抬。该处处于高等减振段,侵限量导致无法设置减振垫,需进行调坡设计。

图4 调坡前隧道竖向侵限情况Fig. 4 Distribution of vertical invasion limit before slope adjustment
3.2 人工调线调坡与智能系统调线调坡结果对比
针对以上侵限情况,设计人员进行了人工调线调坡设计。考虑到人工操作工作量巨大,且第3段曲线侵限问题可通过调整设备支架位置解决,故人工调线设计仅针对第2段曲线进行调整。第2组曲线半径由350 m调整为339 m,该曲线半径将引起曲线限速,由72.87 km/h降为71.71 km/h。调线后,第2段曲线侵限情况得到明显改善,左侧侵限测量点数量由69处减少为13处,最大侵限值为73 mm; 右侧侵限点和侵限值并无变化,最大侵限值142 mm。区间横向总侵限测量点数量共为13+65=78处。人工调坡后,竖向侵限点由107处减少为37处,其中,底部34处,最大侵限值50 mm; 顶部3处,最大侵限值18 mm。
利用地铁智能调线调坡设计系统进行重新计算,系统输入和输出界面分别如图5和图6所示。系统内的超参数设置见表1。本工程隧道内径为5.4 m,对疏散平台要求较高,故调高疏散平台侧的测点侵限权重为2,其他测点均为1。对于容忍值惩罚因子,考虑到疏散平台的宽度要求和轨道的改造代价,将左中2、底点均设为2,其他部位为1。将断面侵限容忍值设置为-50 mm,合规性惩罚因子大小设为2。经系统计算,获得了与人工设计不同的调线调坡方案,结果对比见表2。系统计算微调了第1、3段曲线交点坐标及半径,第2段曲线半径优化为342.79 m,将区间限速改善为72.11 km/h,降低了调线对运营速度的影响。同时,线路横向侵限点数量降至16处,其中,左侧2处,最大侵限值仅25 mm; 右侧14处,最大侵限值62 mm。竖向侵限点为29处,其中,底部26处,最大侵限值44 mm; 顶部3处,最大侵限值19 mm。人工与智能系统调线调坡后横向和竖向侵限情况对比分别见图7和图8。由图可见,不管是线路参数选择的合理性方面,还是侵限情况的改善方面,智能系统的线路调整结果均优于人工操作的结果。

图5 地铁智能调线调坡设计系统输入界面Fig. 5 Input interface of intelligent design system of metro alignment and slope adjustment
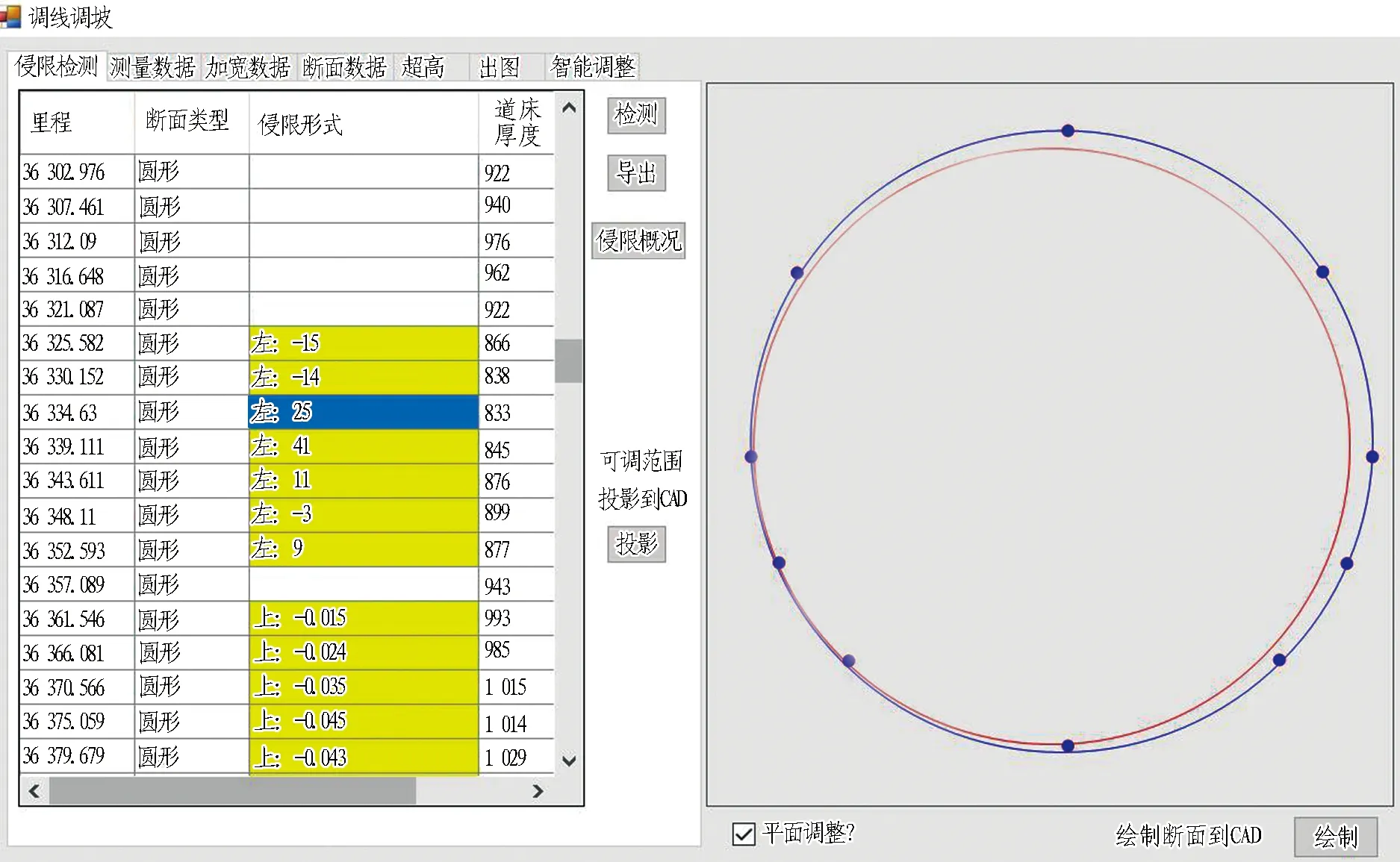
图6 地铁智能调线调坡设计系统输出界面Fig. 6 Output interface of intelligent design system of metro alignment and slope adjustment
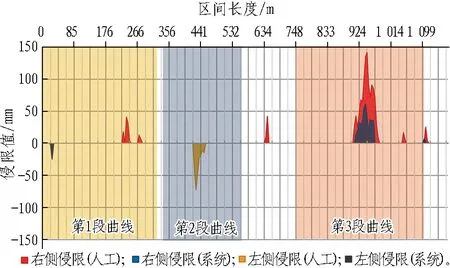
图7 智能系统与人工调线后横向侵限情况对比图Fig. 7 Comparison of lateral limit invasion distribution between system and manual alignment adjustment

图8 智能系统与人工调坡后竖向侵限情况对比图Fig. 8 Comparison diagram of vertical limit invasion distribution between system and manual slope adjustment

表1 系统参数设置表Table 1 System parameters
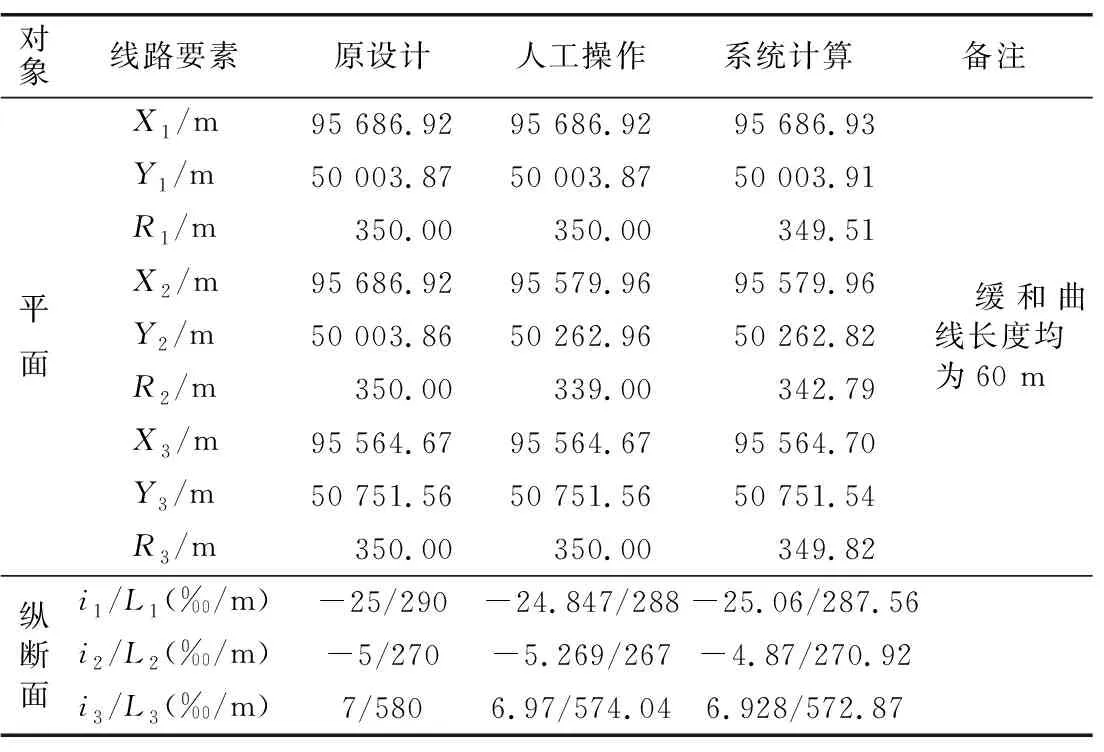
表2 人工操作与智能系统调线调坡结果对比Table 2 Comparison of route elements before and after alignment and slope adjustment
在工作效率方面,人工调线调坡设计需反复调试线路,调整后还需根据新线路数据进行现场复测,这一过程至少需要4d。若侵限情况仍较严重,还需重新设计,设计后再次复测。而智能系统计算自身可形成设计闭环,时间仅需5min。显然,人工设计耗费的时间与智能系统相比差距悬殊。
4 结论与讨论
本文基于人工智能粒子群优化算法,在满足线路设计规范要求的条件下,以减少侵限数量为目标,构建了平、纵断面调线调坡模型,并由此开发了地铁智能调线调坡设计系统,结论如下。
1)粒子群算法具有实用方便、收敛迅速的特点,在求解多约束单目标的最优解问题方面具有较大优势,适合应用于调线调坡技术中。
2)本文详细阐述了地铁智能调线调坡设计系统平面调线和纵断面调坡数学模型的推导过程,创新性地在目标函数内引入了容忍值惩罚项和合规性惩罚项,并可根据断面侵限位置的重要性设置不同的权重,系统计算时优先解决侵限程度大、整改代价高的侵限部位。
3)以长沙地铁4号线某区间右线隧道为例,对比了人工设计和智能系统的调线调坡结果,智能系统无论在线路参数选择的合理性方面还是侵限情况的改善方面,均优于人工操作的结果,且计算时间短,节约了大量人力成本。
调线调坡设计几乎在每条地铁线路中都会遇到,地铁智能调线调坡设计系统有远大的应用前景。现阶段智能系统对断面侵限的权重值设定是靠主观经验判断的,后续将从各线的整改造价、工期量化评价权重的大小,以不断完善系统功能。

