基于区块链的无证书签密方案

张天喜,王利朋,付俊俊,崔 驰,靳梦璐

(1.河南省鹤壁市广播电视台,河南 鹤壁 458030； 2.郑州师范学院,河南 郑州 450044； 3.北京大学,北京 100871)

0 引 言

消息通信服务对签密过程的基本安全要求是机密性和身份验证，其中机密性通过加密来实现，身份验证通过签名来实现。传统的“先签名后加密”方案时间消耗较高。1997年，Zheng[1]首次提出了签密概念，它将签名和加密在同一个逻辑步骤中完成，与传统方案相比，具有更少的计算量和较低的通信成本，实现了效率的提高，是一种较为理想的通信服务方式。传统的公钥密码体制[2]是基于证书的密码体制，用户需要向受信任的证书颁发中心申请证书，证书将公钥与用户的身份绑定。由于对证书的管理成本过高，不利于大规模应用。1984年Shamir[3]提出了基于身份的密码体制，解决了证书管理问题。基于身份的公钥密码体制直接使用用户的身份信息(如ID或电话号码)作为用户的公钥，而私钥需要由可信第三方—密钥生成中心(Key Generation Center, KGC)生成。由于KGC提供用户的完整私钥，攻击者可攻击KGC伪造用户的合法私钥对密文进行解密，因此存在KGC管理不到位的问题。2003年，Al-Riyami等人[4]提出无证书的公钥密码体制，在此密钥系统中KGC只生成用户的部分私钥，需要用户生成剩余私钥并合成完整的私钥。用户的公钥由用户的身份信息和系统参数共同计算得出，这解决了基于身份的密码体制所存在的KGC管理不足的问题。自此，基于无证书签密方案的研究成为了签密领域的研究热门之一。Yu和Wu等人[5-6]提出了基于双线性对的无证书签密方案。但Selvi等人[7]方案中指出了Yu方案没有实现不可否认性和机密性的证明，同样Wu方案也没有解决机密性的问题。Barreto等人[8]提出了在签密和解密过程中不使用双线性对，但在密钥生成阶段需使用双线性对的签密方案运算。俞惠芳和Li等人[9-10]基于双线性对映射的方法提出了可证明安全性的无证书签密方案，并在随机预言机模型下证明了安全性。但由于双线性对的运算开销大，导致基于双线性对的签密方案存在计算量大的问题。针对上述的不足，不使用双线性对的签密方案[11-18]相继被提出。朱辉和刘文浩等人[11-12]提出了无双线性对的无证书签密方案，并且在随机预言机的模型下，基于离散对数(Discrete Logarithm, DL)问题和计算性Diffie-Hellman(CDH)难题证明了方案的机密性和不可否认性。无证书的签密机制具有无密钥托管的优势，国内外的研究者分别提出了将无证书签密机制与物联网[17-21]、无线传感器[22]等网络环境相结合的签密方案。

针对上述问题，本文提出一种基于离散对数(DL)问题与计算性Diffie-Hellman(CDH)难题的签密方案，并对方案的机密性和不可伪造性等安全性进行证明。同时，通过性能分析将本方案与基于椭圆曲线签密方案[18,23-24]的效率进行对比。利用区块链的不可篡改与可溯源的特性对签密验证结果进行上链存储以实现不可否认性。

1 相关工作

1.1 离散对数(DL)问题

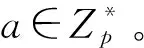
1.2 计算性Diffie-Hellman(CDH)问题

1.3 哈希函数

哈希函数[25-26]是一种压缩映射函数，可以将不同长度的消息映射成较短等长的消息串。具有如下性质：

1)正向计算简单性：给定哈希函数h和消息m,计算h(m)是简单的。

2)逆向计算困难性：对于给定的消息y，计算h(m)=y中的m是困难的。

3)防碰撞性：对于不同的消息m1、m2，使h(m1)=h(m2)在计算上是不可行的。

1.4 区块链

2008年，中本聪在一本关于比特币的白皮书[27]中第一次提出了区块链这一概念。2009年第一块序号为0的创世区块诞生。自此，基于区块链的数字货币相继出现[28]。目前已经从以比特币为代表的数字货币的区块链1.0时代，经过以以太坊为代表的智能合约区块链2.0时代，进入到在社会治理领域的去中心化信任区块链3.0时代。

区块链是一种通过P2P网络节点构建的分布式账本，能够在没有可信第三方的协助下对数据或资源进行溯源。区块链本质上是一个去中心化数据库，具有匿名性、公开透明、可追溯性和不可篡改等特性。基于这些特性，区块链从最初的数字货币扩展到各行各业中，被广泛应用于如金融、医疗和物流信息[29-33]等多个场景。

2 本文方案

2.1 方案框架

本文利用区块链技术，基于离散对数难题，提出一种签密方案。

如图1所示，在本方案的签密模型中，主要包括5个流程。

1)系统初始化。给定一个安全参数χ，KGC计算生成系统公开参数params和系统主私钥s。

图1 签密模型图

2)用户密钥生成。用户根据身份信息ID生成部分私钥，通过安全通道发送给KGC，KGC接收到用户发送的部分私钥并生成另一部分私钥信息，并通过安全通道发送给用户，用户合成个人公私钥信息。

3)消息加密。发送者根据个人公私钥与接收者的公钥信息对消息M进行签名加密形成密文信息c，并将密文信息发送给接收者。

4)消息解密。接收者接收到密文消息c，根据接收者的私钥信息与发送者的公钥信息对密文进行解密并验证。

5)消息上链。接收者将接收到的密文信息c和验证结果上传至区块链。

2.2 方案步骤

1)系统初始化。

KGC运行此算法生成系统密钥和系统公共参数，由下列5步组成：

①选取系统安全参数χ作为输入，KGC选取大素数P形成循环群G，g为循环群G的生成元。

④选取一个已存在的对称加解密算法k,Ek,Dk，其中k为对称密钥。

⑤公布系统公共参数params=〈P,G,g,Ppub,Ek,Dk,H0,H1,H2,H3〉，保存系统主密钥s。

2)用户注册。

KGC和用户合作完成此算法，合成用户的公钥与私钥，由下面4步组成：

③用户ID接收到KGC发送的u、D，计算等式gu=D·gH0(ID,XD)·Ppub·gH0(ID,Ppub)。如果等式成立，则用户计算部分私钥y=u-H0(ID,Ppub)。用户通过SK=x+y合成私钥。如果等式不成立，用户拒绝接收u、D，并通知KGC重新发送。

④用户计算PK=X·D作为自己的公钥并广播PK。

3)消息加密。

此算法由发送者Sen完成，接收者Rec的身份信息为IDRec。流程由下面5步组成：

②计算K=[PKRec·Ppub·gH0(IDRec,PKRec)]r和α=H1(IDRec,R,K)。

③计算k=H2(α,R)，用密文k对消息M进行加密Z=Ek(M||IDSen)。

④计算h=H3(M||IDSen,R,α)和v=SKSen+rh。

⑤密文内容c=〈R,Z,h,v〉，将密文信息发送给接收者Rec。

4)消息解密。

此算法由接收者Rec完成，只有授权过的接收者才能成功运行解密算法。接收者Rec接收到密文c=〈R,Z,h,v〉运行解密算法。由下面4步组成：

①计算K=RSKRec和α=H1(IDRec,R,K)。

②计算k=H2(α,R)，用密钥k解密消息M||IDSen=Dk(Z)。

③计算h′=H3(M||IDSen,R,α)，验证等式h′=h，如果成立，执行下一步；否则拒绝消息M退出解密算法。

④使用发送者的公钥信息，验证等式gv=PKSen·gH0(IDSen,PKSen)·Ppub·Rh，若成立，接收消息M，反之，拒绝接收消息M。

5)消息上链。

此算法由接收者Rec完成，接收者正确解密出消息M后，将密文信息c=〈R,Z,h,v〉与等式gv=PKSen·gH0(IDSen,PKSen)·Ppub·Rh的验证结果上传到区块链上。当对密文信息或发送者身份信息存在争议时，可以从区块链上查看已上传的数据信息。

3 安全性分析

3.1 正确性分析

定理1 用户注册时验证部分私钥信息等式gu=D·gH0(ID,XD)·Ppub·gH0(ID,Ppub)成立。

证明：

gu=g[d+H0(ID,XD)+s+H0(ID,Ppub)]

=gd·gH0(ID,XD)·Ppub·gH0(ID,Ppub)

=D·gH0(ID,XD)·Ppub·gH0(ID,Ppub)

原式得证，等式gu=D·gH0(ID,XD)·Ppub·gH0(ID,Ppub)成立，则用户收到的部分私钥信息正确。

定理2 接收者接收到密文消息后，计算公式K=RSKRec，等式RSKRec=[PKRec·Ppub·gH0(IDRec,PKRec)]r成立。

证明：

RSKRec=[PKRec·Ppub·gH0(IDRec,PKRec)]r

gr·(x+u-H0(IDRec,Ppub))=(X·D)r·gs·r·gH0(IDRec,PKRec)·r

gr·(x+d+H0(IDRec,XD)+s+H0(IDRec,Ppub)-H0(IDRec,Ppub))

=(gx·gd)r·gs·r·gH0(IDRec,PKRec)·r

gr·(x+d)+s·h+H0(IDRec,PKRec)·h=gr·(x+d)+s·h+H0(IDRec,PKRec)·h

原式得证，等式RSKRec=[PKRec·Ppub·gH0(IDRec,PKRec)]r成立，则接收者收到的密文消息正确。

定理3 接收者验证发送者身份的等式gv=PKSen·gH0(IDSen,PKSen)·Ppub·Rh成立。

证明：

gv=gSKSen+r·h

=g(x+y)·gr·h

=g(x+d+H0(IDRec,XD)+s+H0(IDRec,Ppub)-H0(IDRec,Ppub))·Rh

=X·D·gH0(IDRec,XD)·Ppub·Rh

=PKSen·gH0(IDRec,PKSen)·Ppub·Rh

原式得证，等式gv=PKSen·gH0(IDSen,PKSen)·Ppub·Rh成立，则发送者的身份信息正确。

3.2 安全性分析

3.2.1 机密性

定理4A1类敌手的机密性。若敌手A1能以不可忽略的优势ε在多项式时间内赢得相关游戏，敌手A1最多进行qSK次私钥生成询问以及qs次签密询问，则算法F能以不可忽略的优势Adv(F)≥ε·(1-qSK/2k)2/(e(qs+1))在多项式时间内解决CDH问题。

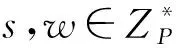
H0询问：当算法F收到A1对H0的询问,,时，若存在记录∈L0，∈L0,∈L0则返回相应的记录给A1；若没有相应记录，A1先对IDi进行公钥生成询问，而后返回表L0中相应的h0给A1。

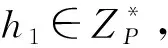
公钥生成询问：收到A1对IDi的公钥生成询问时，算法F进行如下操作。

1)若存在记录∈LPK，返回PKi=XiDi给A1。

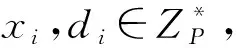
私钥生成询问：当算法F收到A1对IDi的私钥生成询问时，进行如下操作。

1)若存在记录∈LSK，返回SKi=xi+yi给A1。

2)若无相应记录，在对IDi进行公钥生成询问后，再在表LSK中查找相应的元组，并返回SKi=xi+yi给A1。

签密询问：当算法F收到敌手A1对的签密询问时(A1对IDSen已经进行了公钥生成询问)，则F在LPK中查询对应的元组，并进行如下操作。

1)若ηSen=1，则算法F终止模拟。

2)算法F在表LSK和表LPK中分别查找IDSen及IDRec对应的元组和，运行算法签密(params,IDSen,IDRec,SKSen,PKRec,m)，生成相应的签密文c=〈R,Z,h,v〉，返回c给A1。

解签密询问：当算法F收到A1对元组的解签密询问时(A1对IDRec已经进行了公钥生成询问)，在LPK中查询对应的元组，并进行如下操作。

1)若∈LPK，并且ηRec=0，算法F分别在表LSK与表LPK中查询相对应的元组和,运行解签密算法(params,IDSen,IDRec,SKRec,PKSen,c)，返回消息M给A1，若输入的密文c无效，则算法F终止模拟。

2)若∈LPK，并且ηRec=1，当∈L0,∈L1时，计算M||IDSen=Dk(Z)，若gv=PKSen·gH0(IDSen,PKSen)·Ppub·Rh成立，则返回M给A1，否则终止模拟。

3)若表LPK中不存在元组(表示公钥被替换)，当∈L0，∈L1时，计算M||IDSen=Dk(Z)，若gv=PKSen·gH0(IDSen,PKSen)·Ppub·Rh成立，则返回M给A1，否则终止模拟。

挑战：敌手A1输出2个希望挑战的身份(IDSen,IDRec)和2个等长的明文消息(M1,M2)。

收到A1的挑战信息后，算法F对身份IDRec进行了公钥生成询问，获取表LPK中对应元组，并进行如下操作。

1)若ηRec=0，则算法终止模拟。

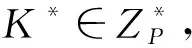
敌手A1经过概率多项式时间次数的上述询问后输出对η的猜测，η′←{0,1}，如果η=η′，算法就输出R(e1+e2)r-1=XDgsgh0作为CDH问题的有效解；如果η≠η′，算法F没有解决CDH问题。

算法F为A1模拟了真实的攻击环境，如果F在模拟过程中未终止，且敌手A1以不可忽略的优势攻破了本方案的机密性，则算法F输出CDH问题的有效解。

令事件ξ1表示敌手A1对挑战身份IDSen和IDRec没有进行过私钥生成询问，Pr[ξ1]≥(1-qSK/2k)2；令事件ξ2表示在询问阶段算法F未终止，Pr[ξ2]≥(1-δ)qS，当qS足够大时，(1-δ)qS→e-1,Pr[ξ2]≥e-1；令ξ3事件表示在挑战阶段算法F未终止，Pr[ξ3]=δ；ξ1∩ξ2∩ξ3表示模拟过程中算法不终止，Pr[ξ1∩ξ2∩ξ3]≥(1-qSK/2k)2/(e(qS+1))。

综上所述，如果算法F在模拟过程中未终止，且敌手A1以不可忽略的优势ε攻破了本方案的机密性，则算法F能以优势Adv(F)≥ε·(1-qSK/2k)2/(e(qS+1))输出CDH问题的有效解。

证毕。

定理5A2类敌手的机密性。在随机预言机模型中，若敌手A2能以不可忽略的优势ε在多项式时间内赢得相关游戏，敌手A2最多进行qSK次私钥生成询问以及qs次签密询问，则算法F能以不可忽略的优势Adv(F)≥ε·(1-qSK/2k)2/(e(qs+1))在多项式时间内解决CDH问题

本定理的证明思路同定理4，不再赘述。

3.2.2 不可伪造性

对签名进行伪造的主要有2类人，一类是Rec本人，一类是除接收者Rec以外的攻击者。

攻击者想要伪造发送者Sen生成密文〈R′,Z′,h′,v′〉使Rec的验证等式gv=PKSen·gH0(IDSen,PKSen)·Ppub·Rh成立。在此过程中攻击者需从最初的签密中解出后续所需要的一些参数k、r，求解这些参数一定会遇到求解离散对数问题，这是在多项式时间内无法破解的。

在解密过程中，接收者Rec伪造签名，此时接收者Rec知道的信息有M、R、Z、h、v。对于签密过程中的等式v=SKSen+rh，由R=gr求解r是求解离散对数难题，攻击者无法在有效时间内通过计算求解。且该等式中含有2个未知变量SKSen和r，而SKSen是发送者Sen的个人私钥，由发送者个人秘密保存，攻击者也无法获得，因此，攻击者无法伪造签名。

3.2.3 不可否认性

方案具有公开验证性，接收者Rec通过计算等式gv=PKSen·gH0(IDSen,PKSen)·Ppub·Rh验证发送者Sen的身份信息，并将结果上传至区块链。因区块链具有公开性和不可伪造性的特性，因此，可以实现签名的不可否认性。

3.2.4 匿名性

4 性能分析

本章将从计算复杂度分析与仿真实验2个方面对签密算法进行对比。

4.1 计算复杂度分析

本文定义以下符号来表示方案中所使用的运算，如表1所示。

表1 复杂度符号表示

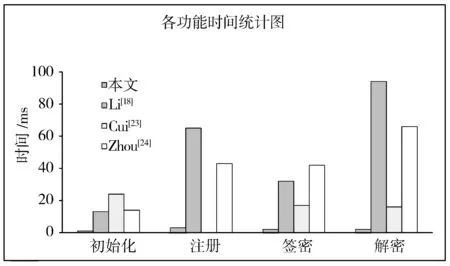
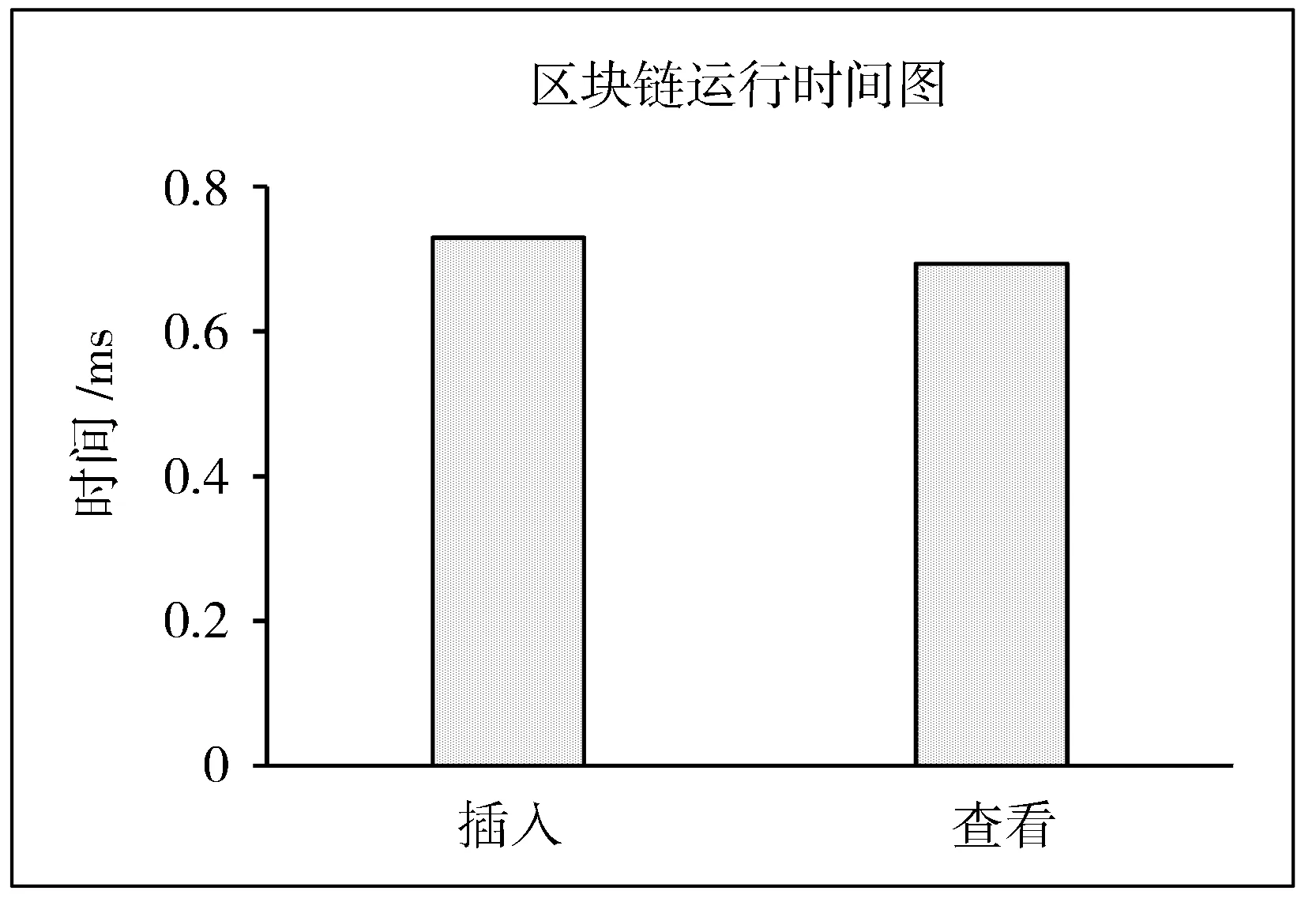
相较于模乘、幂模等运算，模加与模减运算的时间消耗低，故在此省略不计。其中Tmul

表2 性能分析

4.2 仿真实验

本文中的仿真实验采用的操作系统为Windows 10、Intel CPU i7-9750H、My Eclipse2015 CI。将本文与方案[18,23-24]进行仿真实验数据对比，统计初始化、注册、签密和解密4个步骤的耗时，时间单位为ms。文献[18]中涉及的变量n取值为5。文献[18,23-24]所需的椭圆曲线参数参考了JPBC库中Type A类。本文方案所涉及的大数P取8780710799663312522437781984754049815806883199414208211028653399266475630880222957078625179422662221423155858769582317459277713367317481324925129998224791。

图2中的数据重复实验50次取平均值。如图2所示，在初始化阶段，文献[18,23-24]使用椭圆曲线的点乘运算，单次运算的时间消耗约为15 ms，而本文方案在初始化阶段使用幂模运算，时间消耗低于2 ms。本文的注册阶段和签密方案的时间耗时都在3 ms左右。文献[18,24]在注册阶段的时间效率都比本方案低。在签密阶段，文献[18,23-24]的时间效率较低。在解密阶段，文献[18]涉及聚合签密个数n，本实验过程中n取值为5。从图2中可以看出，文献[18]的单个运算效率和文献[23-24]的运算效率都比本文的解密效率低。因此，本文方案在整个签密流程中都有着较高的效率。

图2 签密算法执行时间

本文采用EOS环境模拟本文方案中区块链的运行情况，其设备的具体配置如表3所示。

表3 区块链环境配置表

本文主要利用了区块链的不可篡改性和可溯源性，将密文和接收者对发送者身份验证的结果上链到区块链中。实验测试的区块链运行平均耗时如图3所示。

图3 区块链运行平均耗时

从图3中可以看出，区块链的插入或查看时间远远小于本文方案的签密总耗时。因此，对签密算法的时间开销影响甚微。

5 结束语

本文利用区块链技术提出了一种基于离散对数的无证书签密方案。方案利用区块链的不可篡改性和可追溯性实现了签密的不可否认性，并基于离散对数难题确保了方案的安全性。同时，本文通过标准模型证明了方案具有机密性。性能分析表明本方案性能更优。仿真实验结果显示本方案执行效率较高，且数据上链耗时对签密过程的总耗时影响较小可忽略不计。