二维弹性波自适应网格有限差分模拟方法*

张春丽，张伟

1. 中国科学技术大学地球和空间科学学院，安徽 合肥 230026

2. 南方科技大学深圳市深远海油气勘探技术重点实验室，广东 深圳 518055

3. 南方科技大学地球与空间科学系，广东 深圳 518055

1 背 景

地震波数值模拟是复杂介质逆时偏移成像和全波形反演的基础。有限差分法（FDM）由于易于理解和实施，网格生成简单，易于进行大规模并行计算等原因，是地震波成像和反演最主要的地震波正演方法。提高地震波有限差分模拟的计算效率，可以显著节省地震波成像和反演工作的成本。有限差分模拟的计算资源需求与格点数量和时间步数量近似成正比，对确定的计算区域和时间窗长度，网格步长越小则网格数越多；时间步长越小则时间步数越多。为压制数值频散和耗散误差，网格步长需要在所有的网格点上满足所用格式的每波长网格点数要求，如果使用均匀网格离散模型，则网格步长由整体速度模型中的最低速度决定。另外，离散几何形状复杂尖锐的散射体，例如地质尖灭，也需要使用较小的网格步长。而在速度值高的区域和速度变化平缓的区域，全局细网格会造成空间过采样（图1（a））。此外，由于显式时间积分格式稳定条件限制，在高速区采用较小的空间步长时，需要同时采用较小的时间步长。综上所述，对于速度差异大的复杂介质模型，采用均匀网格进行地震波模拟会导致空间和时间过采样，浪费计算资源，增加计算时间。

克服均匀网格计算效率低的问题的一种方法是采用可变网格。可变网格可按照网格步长是否连续变化分为两类。文献［1］最早提出了一种简单的网格步长连续变化的方案［2-4］，如图1（b）所示。由于和均匀网格相比，网格的拓扑结构没有变化，所以在粗细网格的波场间不需要进行变量信息交换；然而，由于细网格区域会不可避免地从目标细化区延伸至计算区域边界，所以这种方案只是部分减少了网格数，并且对于时间步长过小问题没有显著改善。另外一种可变网格是间断网格，即网格步长在变化边界突变整数倍，如图1（c）所示。同级网格覆盖区域呈现层状或者块状［5-8］。与连续变化的可变网格相比，间断网格更为灵活，减少了计算的网格点数。但在低速体形状不规则时，受网格区域简单几何形状的限制，间断网格仍然会细化部分非目标区域造成浪费。

自适应网格（AMR，adaptive mesh refinement）由一系列边界形状不规则的多级网格块组成，如图1（d）所示，能够灵活地覆盖不规则的目标细化区域。从图1中的不同类型网格的格点数目可以看出，自适应网格可以最大化减少不必要的网格数，是比间断网格更为高效的网格划分方案。文献［9］最早提出自适应网格技术，同有限差分法结合，用于求解双曲型偏微分方程；文献［10］提出了一种格点聚类算法（point clustering）用于自适应网格的自动生成。在弹性动力学领域，许多研究者将自适应网格算法应用到有限体积法（finitevolume method）或者间断伽辽金方法（discontinuous Galerkin method）中：文献［11］提出使用高阶间断伽辽金和自适应网格模拟固液耦合介质中波场的传播。文献［12］在二维声波方程有限差分模拟中实现了自适应网格，显著提高了复杂速度模型中的声波模拟效率。由于弹性波方程比声波更为复杂，在相同网格点需要定义更多的变量，导致实现自适应网格难度更大，目前尚未见到基于自适应网格的弹性波有限差分模拟算法，本文将首次实现二维弹性波模拟的自适应网格有限差分算法。

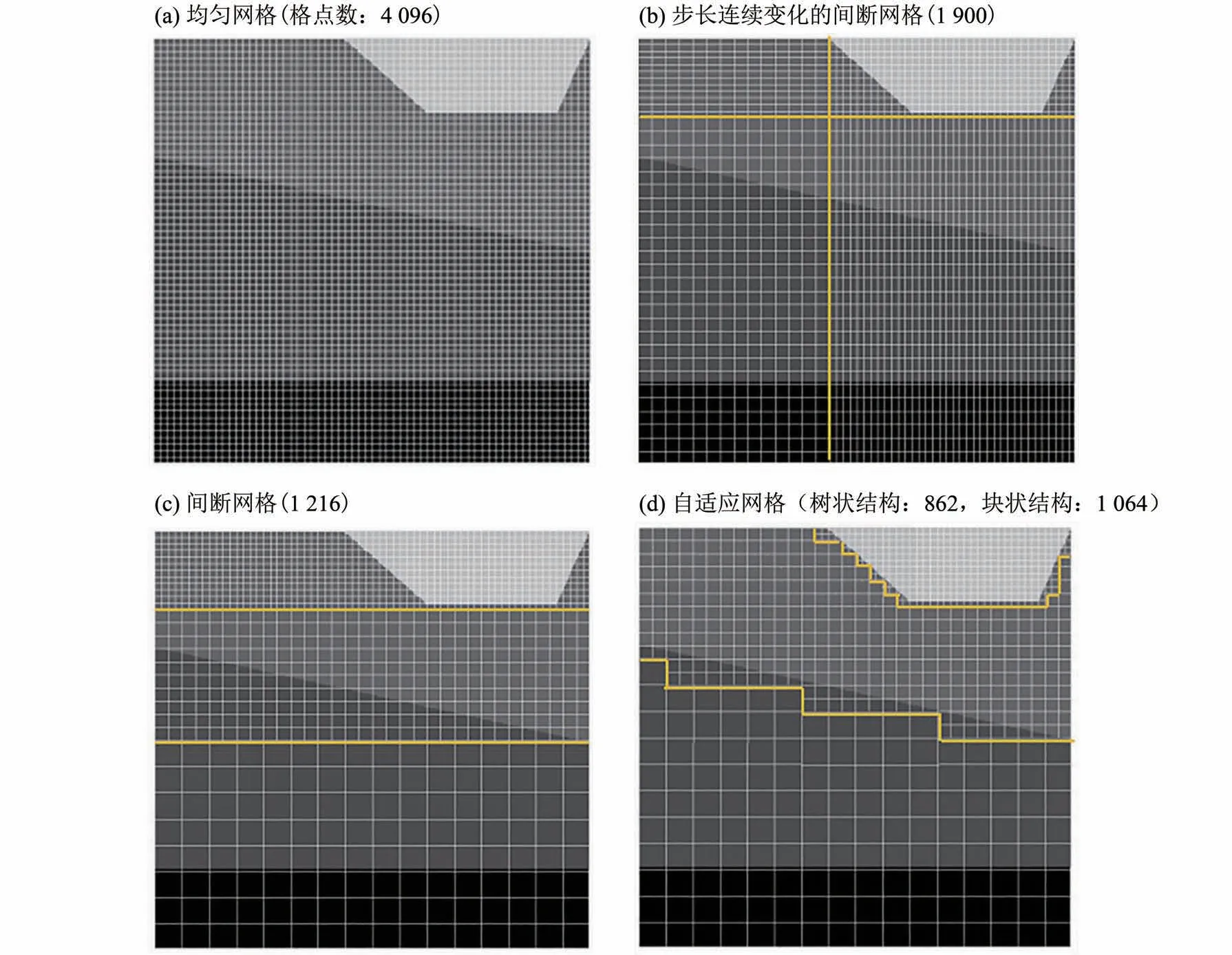
图1 不同类型的网格和格点数（灰度值表示波速，黄线表示不同网格步长区域的边界。）Fig.1 Different grids and corresponding numbers of grid points(The gray values indicate the velocities of geological bodies,and the yellow lines represent the boundary between patches of different grid spacings.)

2 二维弹性波控制方程与同位网格有限差分算法

本文求解二维一阶速度应力方程组形式的PSV波方程，该方程组的矢量形式为

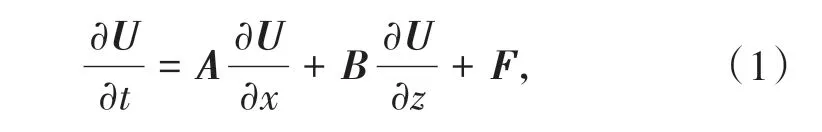
其中U为速度-应力矢量：

其中vi代表i方向的速度分量，σij代表应力分量。震源项

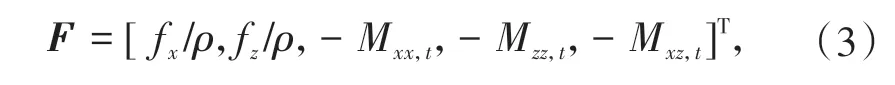
其中ρ代表密度，fi表示体力，Mij，t表示地震矩张量关于时间的导数。系数A和B分别是

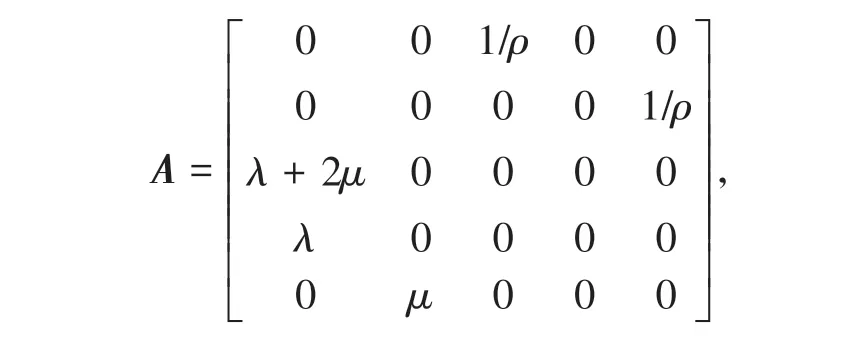
其中λ和μ是Lamé常量。

空间域采用中心差分格式对方程进行求解。以x方向为例，同位网格空间精度为2N阶的中心差分格式为

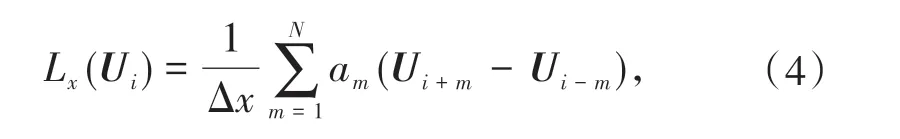
其中下标表示空间索引，Lx表示x方向的空间差分，Δx表示空间步长。我们使用八阶精度的差分格式［13］，N= 4，系数分别为a1= 4/5，a2= -1/5，a3= 4/105，a4= -1/280。

时间域采用如下的四阶Runge-Kutta 时间积分格式，

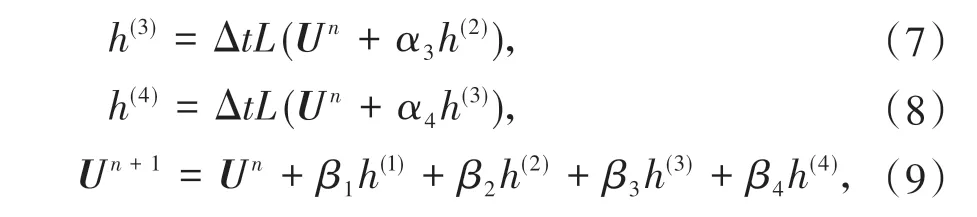
其中Un表示时间步为n时波场各分量的值，L(U) =ALx(U) +BLz(U)，Δt表示时间步长，系数分别为α2=α3= 0.5，α4= 1，β1=β4= 1/6，β2=β3= 1/3.

为了解决中心差分格式的奇偶失联导致的不稳定问题，我们还进行了显式滤波处理［14］。求解得到下一时刻的波场值Un+1后，对其应用模板长度为2N+1 个格点的滤波算子进行滤波处理。滤波算子可以表示为（以变量q为例）

其中

3 自适应网格有限差分法求解弹性波方程的实现

在有限差分模拟方法中实现自适应网格，需要选择或实现以下几个关键部分：数据结构，多级网格生成，不同级别网格间的波场交换，以及施加边界条件和震源。

3.1 数据结构

用于实现自适应网格的数据结构方案主要有两种：树状结构的自适应网格［15］和块状结构的自适应网格［16］。树状结构的自适应网格使用四叉树（二维）或八叉树（三维）的数据结构。块状结构的自适应网格使用的是常规的线性表结构，将细化的目标区域使用一系列形状类似，包含格点数量相近的矩形网格区进行离散［10］，负载均衡将在这些矩形区域的基础上进行。和树形结构相比，块状结构的自适应网格实现方式较简单，能够访问离当前格点较远的波场值，与本文采用的八阶格式的长差分模板适应，因此本文采用块状自适应网格结构。我们采用Berkeley Lab 开发的自适应网格框架AMReX［16］解决自适应网格复杂的数据结构带来的网格生成和管理问题，生成网格的具体流程在下一节中详细介绍。

3.2 网格生成

自适应网格框架AMReX 提供了自适应网格生成的函数接口，使用时只需以数组形式给出每个网格点的某个物理量取值，以及以该物理量取值为标准的细化阈值，则AMReX 函数自动将需要细化的网格进行标记（设置特定取值）。图2 展示了三级自适应网格生成过程。首先我们要计算基网格，也就是最大的网格步长，使用基网格划分整个计算模型（图2（a））；然后按照某种标准对需要细化的目标网格区域进行标记（图2（b）），其中黄色点划线表示标记出的在基网格基础上需要细化的区域，使用集群算法将被标记的所有点整合，划分整理成组成下一级网格的网格块（图2（c））。每一级网格都重复此步骤进行生成（图2（d）），直到达到需要的最小网格步长。图2（d）中覆盖表层高速区的细网格将在后文自由表面条件实现中进行介绍。需要并行计算时，程序将按照每个网格块的点数，将各网格块分配给各个进程，进行负载均衡。在本文中，细化标准选择为每级网格的步长将保证每波长格点数（PPW）满足减少数值频散的精度需求。考虑到使用的八阶精度的中心差分格式和波传播路径的长度，本文采用PPW=6以兼顾精度与效率。

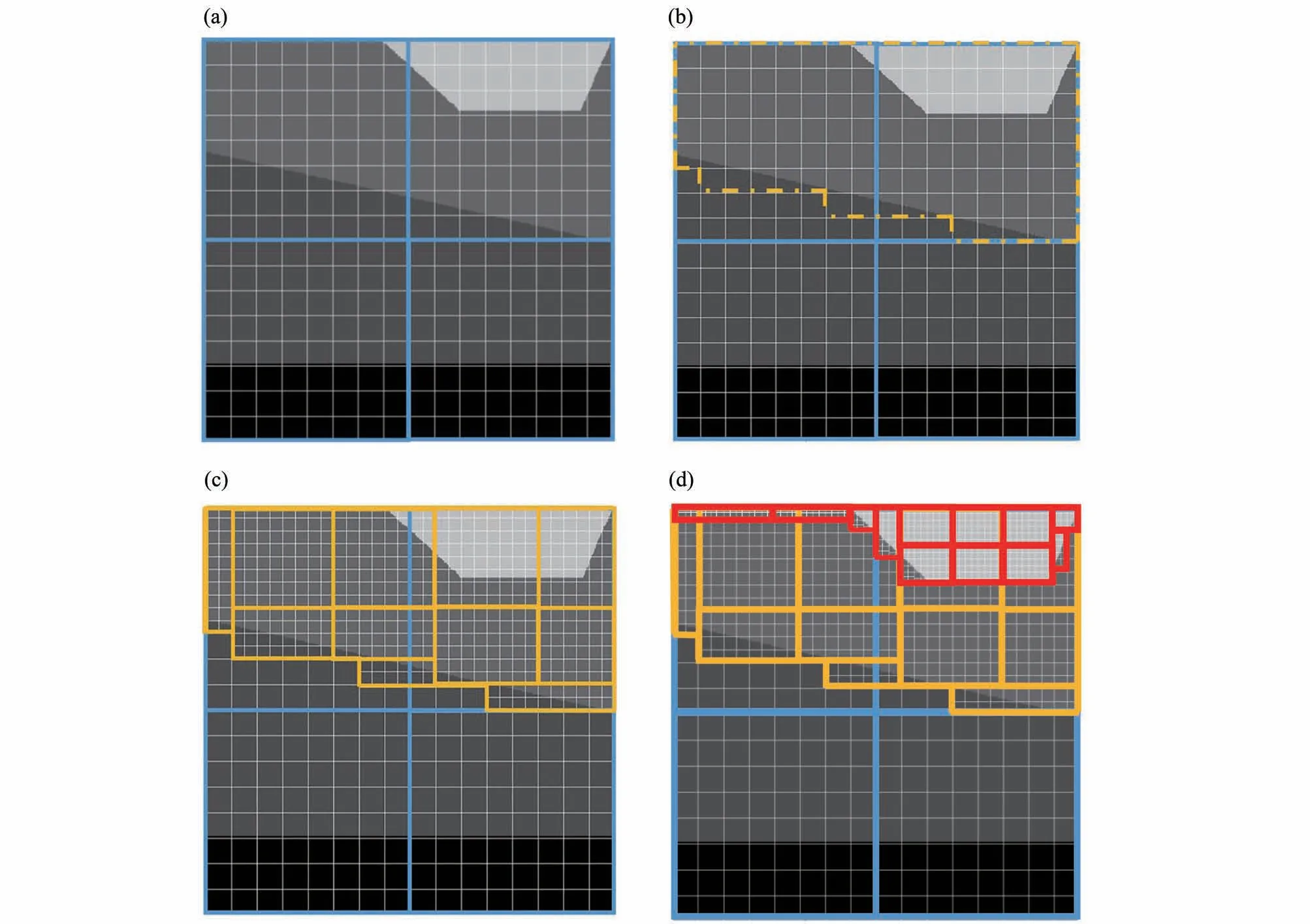
图2 三级自适应网格生成过程（灰度图表示速度模型，较浅色块表示低速的需要细化的区域）Fig.2 Scheme of AMR grid generation with three levels

对于给定的速度模型，最小网格步长hmin可以按照模型最小速度vmin，震源最大频率fmax和PPW来计算，即

本文采用固定的相邻级别网格步长比为2。继续计算其他各级粗网格的步长，理论基网格步长hmax可以使用模型最大速度vmax来估计

实际使用的基网格步长应该小于等于这个值。本文计算基网格步长时采用的速度值略小于模型最大速度，目的是保证基网格作为最高级别网格的覆盖范围不会太小。

3.3 粗细网格信息交换

不同级别网格间的波场交换分为两个部分：从粗网格波场到细网格波场的插值操作，目的是计算细网格区域边缘点差分模板缺失的格点波场值；从细网格波场到粗网格波场的降采样操作，目的是使计算稳定。

对于粗网格到细网格的波场传递，本文采用之前相关研究中普遍采用的双线性插值的方法［5，17-18］：

其中Wc和Wf分别是粗网格和细网格上的物理量，F(i)和N(i)用于计算细网格点周围空间距离最近的粗网格点的索引，

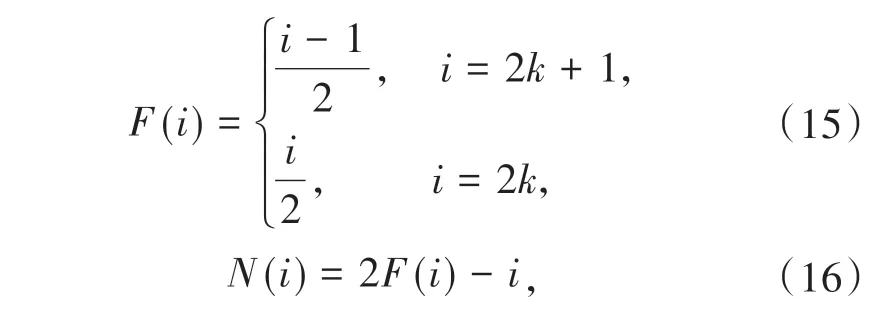
Ai是插值系数，可以由粗细格点的空间位置计算得到［19］：A1= 9/16，A2=A3= 4/16，A4= 1/16.

对于细网格到粗网格的波场传递，本文采用以下公式由细网格波场获得粗网格点的波场值：

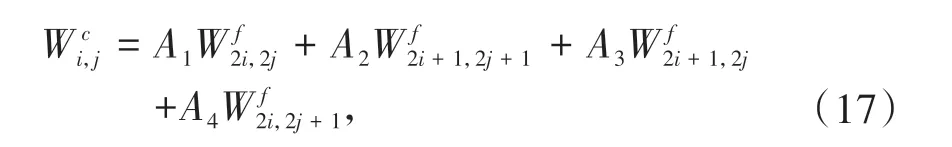
其中系数取值A1=A2=A3=A4= 1/4.

粗细网格边界处各类点的空间分布见图3。

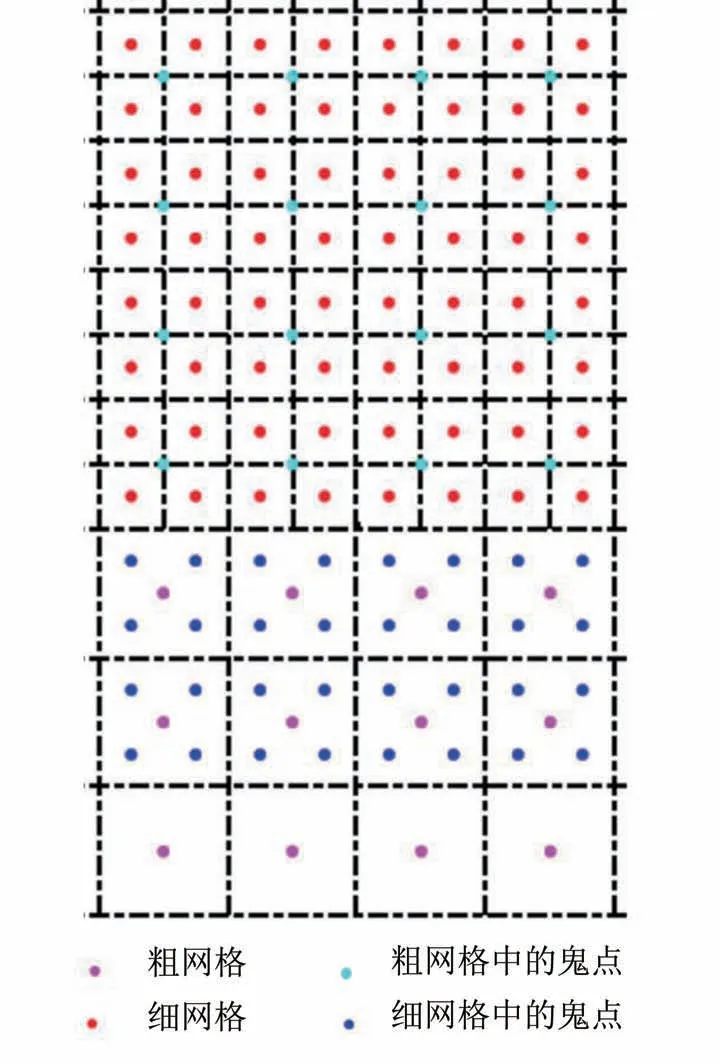
图3 自适应网格波场空间分布Fig.3 Wavefield variable locations in AMR

3.4 边界条件和震源施加

本文采用海绵层吸收边界［20］吸收来自人工截断边界的虚假反射。在不同位置采用相同物理长度的吸收层。采用应力镜像法施加自由表面边界条件。为确保稳定性，在接近地表的位置速度和应力计算均采用降阶处理。由于自适应网格中不同等级网格点空间位置不会相互重合，如果地表层的介质（按照波速）需要不同等级的网格进行离散，地表格点的深度将无法一致，所以我们将自适应网格的地表层处理成同级的、地表最小速度需要的网格等级（如图2（d））。

本文施加震源时，采用同时在震源点周围的高斯分布上的点同时加源的平滑处理，避免震源处空间差分的奇异性：

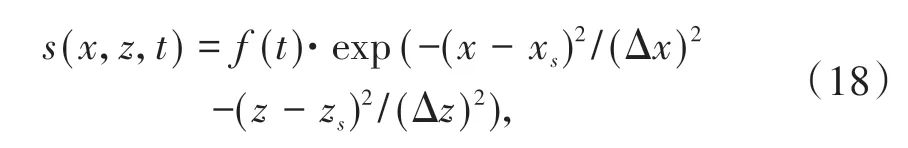
其中(xs，zs)为震源点空间坐标，(x，z)为周围点坐标（xs-x≤dx），f(t)是震源时间函数。

本文使用自适应网格进行弹性波有限差分模拟的主要步骤为：①输入计算参数；②生成自适应网格；③从基网格到最高级网格，依次遍历每级网格，求解弹性波方程；④使用粗网格点的波场值计算细网格边缘模板缺失的值；⑤使用细网格点的波场值重新计算与细网格重叠的粗网格的部分波场值；⑥重复步骤3 到步骤5 直到最终的时间步；⑦输出结果。

4 数值算例

我们使用4个模型对本文提出的自适应网格方法的准确性和稳定性进行测试：均匀半空间模型、层状模型、盆地模型和SEAM 模型。自适应网格中的网格级别从0开始计数，使用h0表示基网格空间步长，使用hn表示第n级网格的空间步长。

4.1 均匀半空间模型和层状模型

我们首先使用自适应网格模拟均匀半空间模型中弹性波的传播，并将结果和常规的使用均匀细网格的结果作比较。半空间均匀模型中只有地表是不连续面，可以排除其他因素的影响，通过简单的震相直观地显示波场在不同级别的网格传播时产生的误差。模型纵波速度为6 900 m/s，横波速度为4 000 m/s，密度为2 600 kg/m3。使用爆炸源，震源时间函数为主频为2.67 Hz 的雷克子波。使用两级的自适应网格对模型进行划分，由于震源最高频率是6.67 Hz（约2.5倍主频），我们设置基网格步长h0= 100 m（PPW=6），h1= 0.5h0=50 m 呈层状分布，粗细网格交界处位于z=8 100 m（图4）。设置时间步dt=0.002 s，使其满足稳定性条件。使用厚度为800 m 的指数吸收边界吸收来自计算区域的截断边界的虚假反射。我们使用全局细网格（h= 50 m）的计算结果作为参考解。

图4 半空间均匀速度模型Fig.4 Homogeneous half-space velocity model

计算得到的vx分量在1.2 s和2 s时的波场快照如图5。由图5可知，在自适应网格的波场快照中，在粗细网格边界处没有明显的由波场交换引起的虚假反射。和全局细网格相比，只有在吸收边界处有明显差异。由于不同位置粗细网格的吸收边界物理长度一致，细网格处吸收层数多，衰减程度高于粗网格。图6展示了自适应网格和全局细网格得到的vx和vz分量（接收点坐标见图4），模拟记录的最高频率是震源子波主频的2.5倍。在每个接收点处，二者波形无明显差异。我们计算了各个接收点的两组波形从0 s 到6 s 的单值包络误差EM（single-valued envelope misfit）和单值相位误差PM（single-valued phase misfit）［21-22］。这种误差标准基于连续小波变换，可以区分包络误差和相位误差。EM和PM表达式分别为

图5 均匀半空间模型弹性波模拟的波场快照Fig.5 Snapshots at 1.2 s and 2 s for the homogeneous half-space model

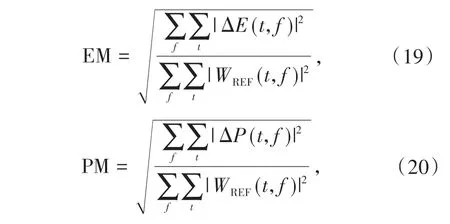
其中WREF(t，f)是参考解进行连续小波变换的结果，ΔE和ΔP分别是自适应网格计算得到的波形经连续小波变换的结果W(t，f)与WREF(t，f)的包络误差和相位误差，具体公式见文献［21］。文献［22］中将同时满足|EM|＜0.2 和|PM|＜0.22 的两组波形的拟合程度评价为“excellent”。我们将每个接收点的包络误差和相位误差分别标记在图6中。可以看到，因为2 号和5 号检波点的vx分量能量微弱，吸收边界没有完全吸收的能量占主导，自适应网格吸收边界的吸收效果和全局细网格的吸收效果有差异，所以EM 和PM 值较大。与均匀细网格不同，自适应网格的震源位于粗网格中。5 号检波器距离震源较近，所以vz分量误差较大。其他4 个检波点的vx分量及全部检波点的vz分量的误差都远小于“excellent”等级的误差标准。由此说明，使用自适应网格模拟弹性波传播时，模拟结果比较准确。

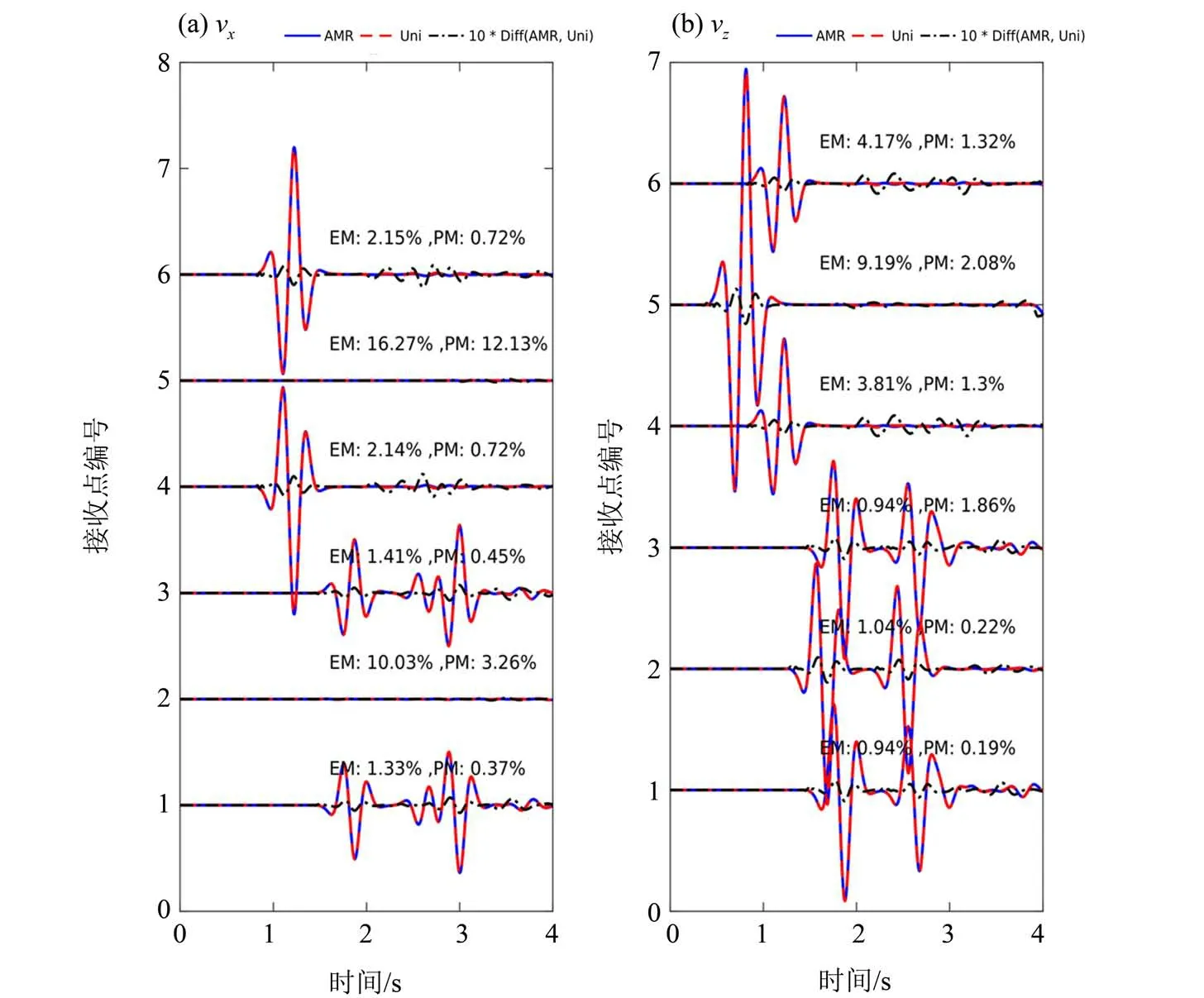
图6 自适应网格和全局细网格的地震记录（接收点位于图4）Fig.6 Comparison of the velocity components calculated with the AMR grid and those with the uniform grid at receivers in Fig.4

另外，我们将自适应网格震源位于细网格（震源坐标为10 025 m 和5 025 m）和粗网格（震源坐标为10 050 m 和12 050 m）情况下的波场计算至第10万步（时间=200 s），将各接收点的分量记录展示在图7 中。图7 显示在长时程模拟的过程中波形是稳定的，表明了自适应网格算法的稳定性。

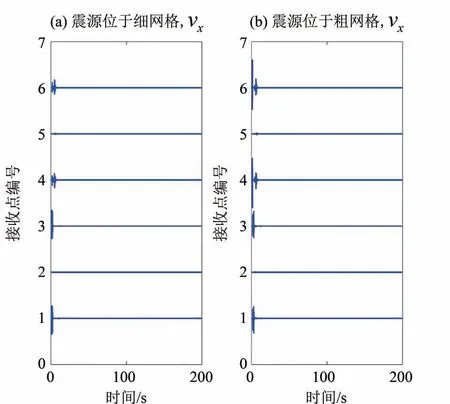
图7 自适应网格均匀半空间模型长时模拟结果Fig.7 The results of long time simulation using AMR for homogeneous half-space model

自适应网格提高地震波模拟计算效率，一方面是通过减少网格数，更重要的一方面是自适应网格可以在满足稳定性的条件下，显著增大了时间步长。我们通过层状速度模型来展示自适应网格对时间步长的增加效果。所用的三层速度模型由浅到深的横波速度分别是800 m/s，1 600 m/s，3 200 m/s，纵波速度分别是1 386 m/s，2 771 m/s和5 543 m/s，密度分别是2 300 kg/m3，2 500 kg/m3和2 600 kg/m3。爆炸源的震源时间函数为主频为2 Hz 的雷克子波。使用三级自适应网格，由浅到深的基网格，一级网格和二级网格的空间步长分别是100 m，50 m 和25 m。图8 展示了速度模型、网格分布和观测系统。图8中黑色实线表示速度界面，黑色虚线表示不同级别间网格的边界。覆盖从浅到深的层的最细网格分别是二级网格，一级网格和基网格。由于稳定性条件，如果采用全局均匀细网格计算，稳定的时间步长为dt=0.005 s。而自适应网格由于在最高速区域的网格步长更大，稳定的时间步长为dt=0.01 s。

图9 比较了接收点处（见图8）自适应网格和全局细网格计算得到的速度分量。可以看到拟合程度较高。时间效率方面，与全局细网格相比，自适应网格将需要进行计算的网格点减少到约26%，由于时间步长大，计算时间减少到约15%。该测试表明自适应网格可以从网格数和时间步长两个方面提高模拟的效率。

图8 层状模型及网格分布Fig.8 The layer model and the refinement scheme

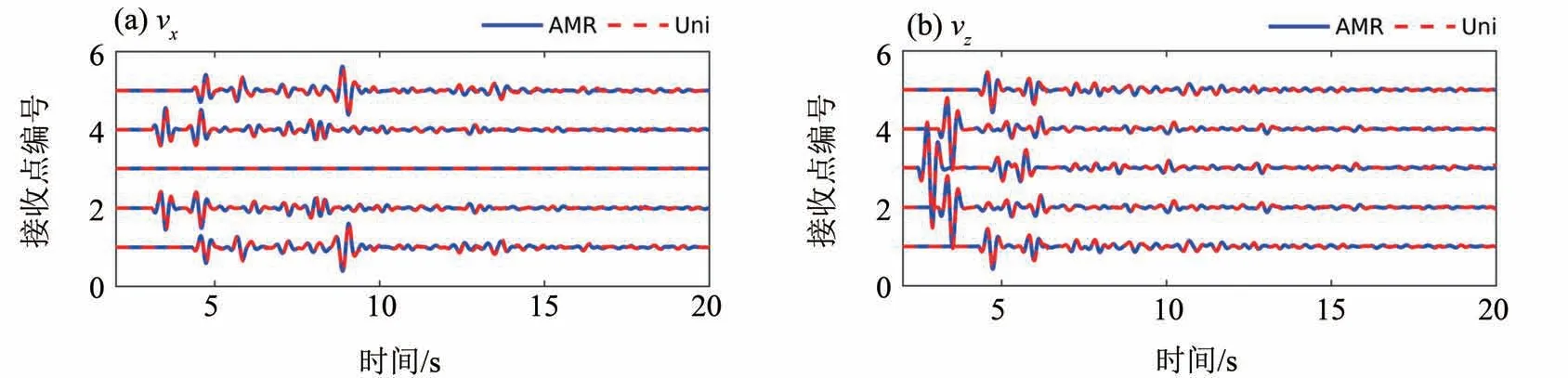
图9 层状模型自适应网格和均匀细网格计算结果比较Fig.9 Comparisons of the velocities in x-and z-direction calculated with the AMR and uniform finer grid for the layer model

4.2 盆地模型

沉积盆地内部经常存在较厚的低速风化层，地震波传播进入盆地后，其能量会陷入在盆地中，导致地震动幅值增大和地震动持续时间增加的现象。准确模拟地震波在盆地模型中的传播是强地面运动模拟的关键。使用数值方法模拟地震波时，由于盆地内速度往往较低，需要使用小网格，导致计算量增加。已有研究表明，即使只计算低频地震波，不使用等效介质参数处理时，粗网格计算的低频地震动和细网格计算结果也会存在较大差异［23］。自适应网格可以帮助解决这类问题：在低速区使用较小空间步长，在高速区使用较大空间步长，由此达到准确模拟波场的同时，节省计算资源的目的。本例中，我们使用自适应网格模拟弹性波在盆地中的传播，将结果和常规的使用均匀细网格的结果作比较。

用于测试的速度模型中含有两个低速盆地，形状分别为直角梯形和矩形，如图10 所示。两个盆地的介质的纵波波速为2 500 m/s，横波波速为650 m/s，密度为2 300 kg/m3；围岩的纵波波速4 500 m/s， 横 波 波 速 为2 600 m/s， 密 度 为2 600 kg/m3。

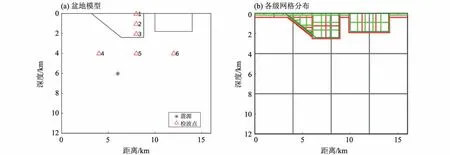
图10 （a）盆地模型，（b）各级网格分布Fig.10 （a）The basin model，（b）Diagram of grid refinement

爆炸源采用震源时间函数为主频4.34 Hz 的雷克子波。最大与最小的横波速度比值为4，本次试验采用三级的自适应网格进行计算。考虑到震源的最大频率和模型速度值，我们设置基网格步长h0=40 m 覆盖整个计算区域，第2 级网格（h2=10 m）对两个低速盆地进行划分，基网格和第2级网格间有第1级网格过渡，以满足相邻网格级别连续的要求。具体做法是设置过渡层的最小宽度，每个网格块的范围由自适应网格框架自动生成。第二级网格包含部分高速区，避免低速区部分格点的差分模板包含粗网格点。根据速度模型自动生成的各级网格的空间分布如图10（b），深灰线、红线和绿线分别表示基网格，1 级和2 级网格块的边界。采用这种网格步长设置方式，满足压制频散误差的每波长格点PPW≥6 的要求。设置时间步长dt=0.002 s 满足稳定性要求。震源点和检波点的位置如图10（a），另外，我们在地表设置测线。我们将自适应网格的模拟结果和全局细网格（空间步长h=h2= 10 m）得到的参考解进行比较。

图11 比较了自适应网格和全局细网格在时刻t=1.2 s 和时刻t=2 s 的波场快照。为排除吸收边界的影响，波场快照内没有包含吸收层区域。由图可知，除吸收边界外，使用全局细网格和自适应网格得到的结果相差不大；在t=2 s 时，可以看到地震波在盆地内的能量很强，而盆地周围的波场能量微弱。图12 比较了几个接收点处（见图10）自适应网格得到的速度分量和全局细网格得到的速度分量。1～3 号检波点位于盆地内（2 级细网格），4～6 号检波点位于高速围岩区域（粗网格）。自适应网格和全局细网格的指数吸收边界的吸收效果很难做到完全一致，这种差异在波形上有所体现。整体拟合程度较高。为了定量地评估两种方法得到的波形的拟合程度，我们使用从0～24 s的各接收点的x和z方向的速度分量计算了EM 和PM值，结果也展示在图12 中。所有检波点的EM 和PM 值均小于“excellent”水平的误差阈值。盆地内部1～3 号和6 号检波点的vx的EM 值较大：6 号检波点可能是因为地震波振幅较小，受吸收边界吸收效果差异的影响比较大。1～3 号检波点vx分量的主要能量比较集中在波场能量在盆地内多次反射的时段，对整体误差影响大，而4～6号的vx分量主要能量集中在直达波，自由表面反射和前几次盆地下界面反射的时段；vz分量的主要能量出现的时段在1～6号检波点相似。自适应网格波场的误差随传播逐渐积累，所以相比4～6 号检波点，1～3 号检波点的vx误差明显偏大，vz误差接近。图13是在地表测线处使用全局细网格和自适应网格的计算得到的水平速度分量和垂直速度分量，可以看到，自适应网格计算结果和全局细网格的计算结果无明显差异；另外，由于地震波能量被盆地捕捉，地表测线的各检波点（除在盆地范围外，横坐标10 km左右）在很长时间内一直存在地震波能量。

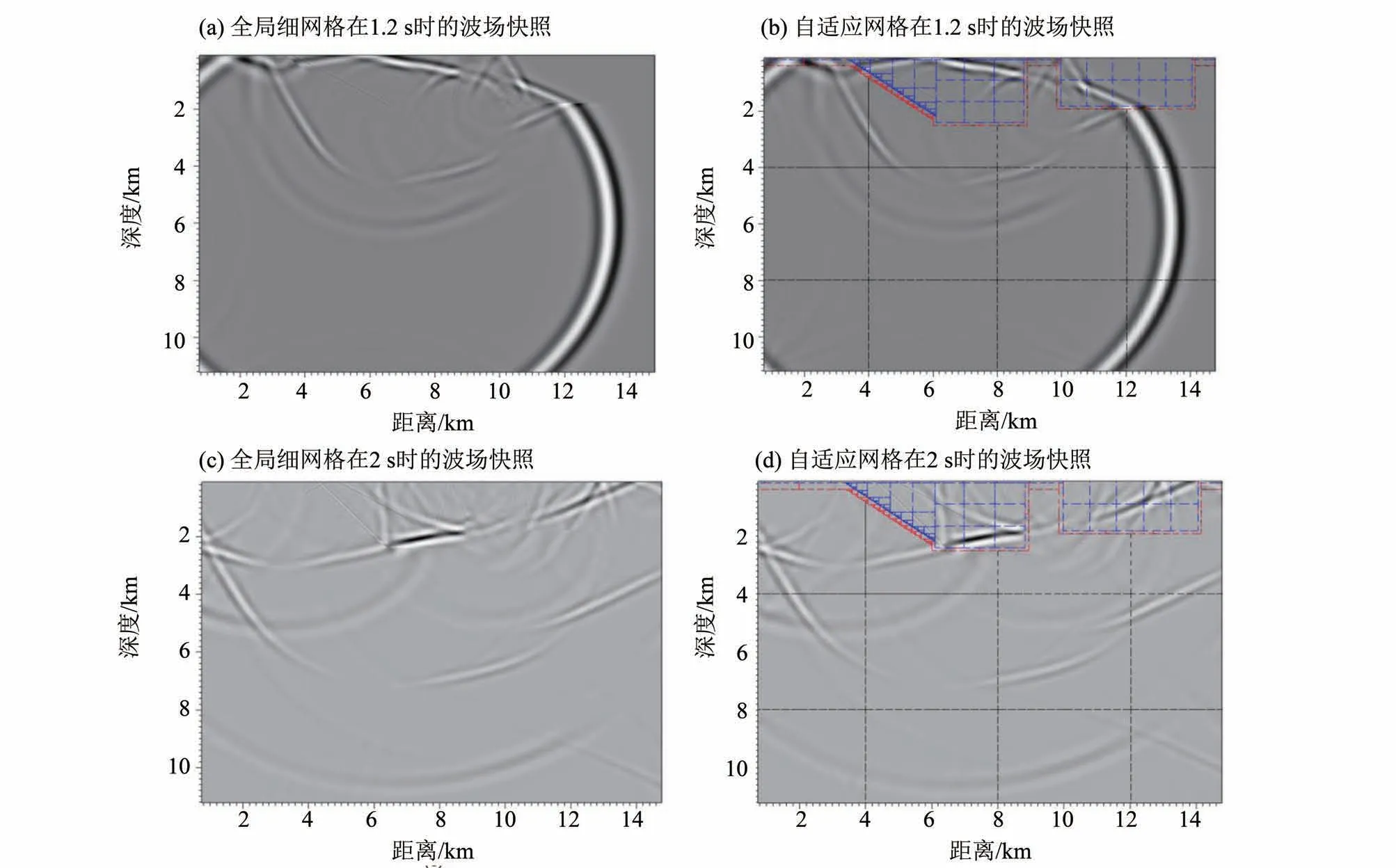
图11 盆地模型弹性波模拟的波场快照（同一时刻的波场快照的色标的最大值调整至全局细网格波场快照振幅的最大值）Fig.11 Snapshots at 1.2 s and 2 s for the basin model(The maximum values in grayscale bars of the results at the same moment have been adjusted to the maximum value for the corresponding result using the uniform grid.)

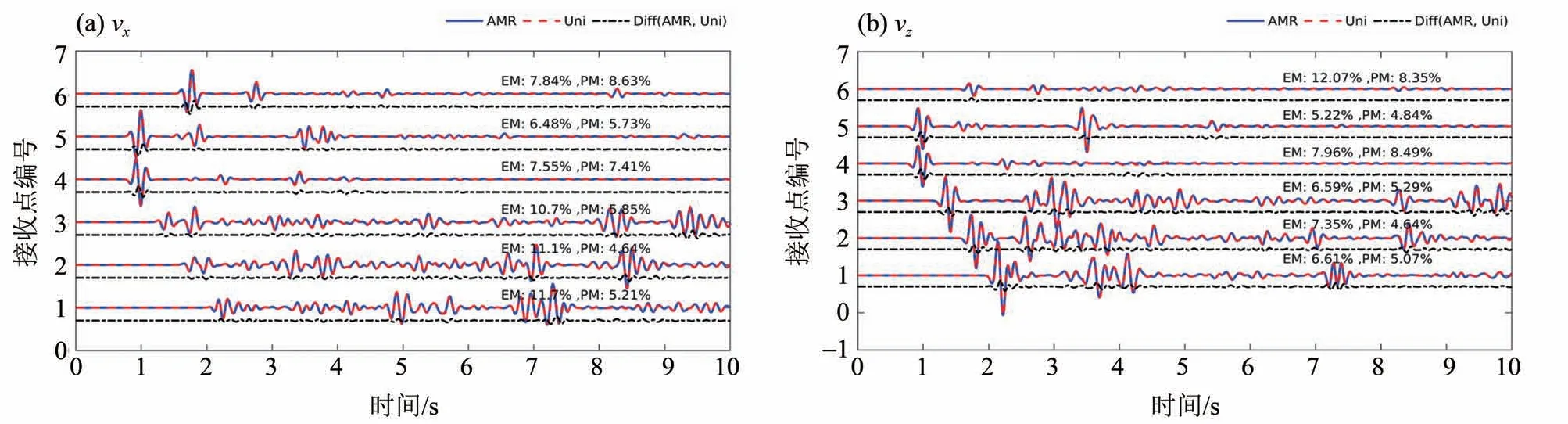
图12 使用自适应网格和全局细网格模拟弹性波在盆地模型中的传播得到的地震记录，接收点见图10（a）Fig.12 The velocity components calculated with theAMR grid and those with the uniform grid at receivers in Fig.10(a).

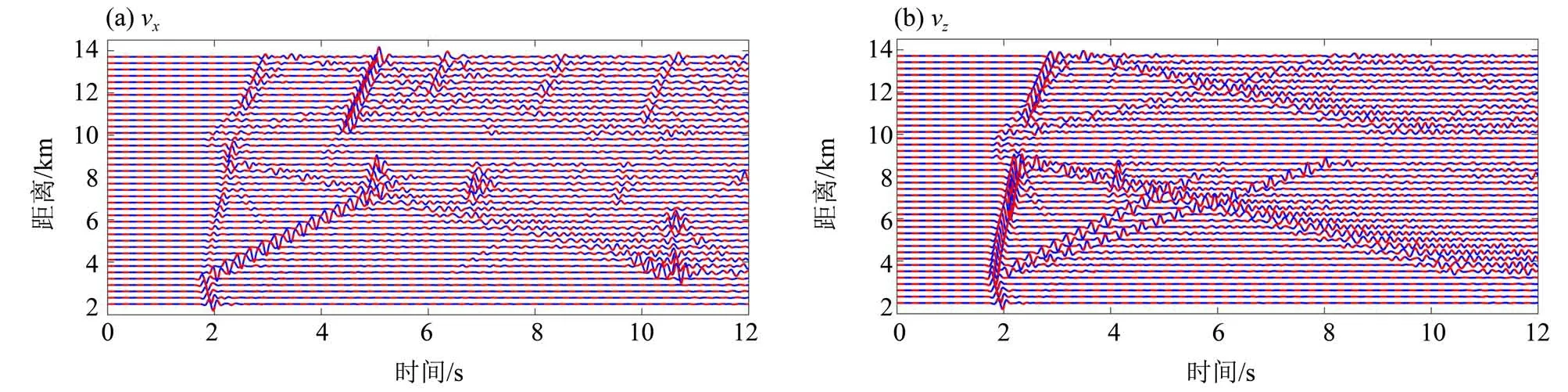
图13 使用自适应网格模拟弹性波在盆地模型中的传播得到的地表测线的结果，和全局细网格得到的参考解做比较Fig.13 Comparison of the velocity components for the receivers at the survey line calculated using the AMR grid and those using the uniform grid

时间效率方面，与全局细网格相比，自适应网格将需要进行计算的网格点减少到18%，计算时间也减少到约18%。自适应网格中除求解弹性波控制方程之外消耗计算时间的来源，主要包括粗细网格波场交换和自适应网格复杂的存储结构（可能破坏内存访问的局部性，影响内存访问效率）。这些因素在本次测试中几乎没有影响。本次测试的结果证实了自适应网格模拟的准确性和高效性，以及在强地面运动模拟场景下的适用性。

4.3 SEAM模型

为测试自适应网格在更复杂的模型中的有效性，采用的速度模型来自国际勘探地球物理学家学会的先进模拟计划第一期（SEAM Phase I，SEG advanced modeling program）［24］。SEAM 一期的盐下三维模型（SEAM Phase I subsalt earth model）取自墨西哥湾的一个深水盐域，本次测试使用的是这个模型的一个二维剖面，截取的是北坐标等于23 900 m 的位置。本次测试在原模型的基础上进行了部分调整：将原模型的横波速度为0的海水部分改成横波速度600 m/s。SEAM 模型的内部速度变化复杂（见图14）。图14中伪彩色图表示横波速度，灰线、红线和绿线分别表示基网格、一级网格和二级网格块的边界。使用爆炸源，震源时间函数是主频为4 Hz的雷克子波。

自适应网格基网格步长h0= 40 m，1级网格步长h1= 0.5h0= 20 m，2 级网格步长h2= 0.5h1=10 m，1 级和2 级网格的划分标准是横波波速分别小于2 400 m/s 和1 200 m/s，使得每波长网格点数满足压制数值频散的要求。基网格和2级网格中间存在1 级网格进行过渡。图14 展示了三级自适应网格的空间分布，可以看到浅层的海水和低速沉积层由第2级网格覆盖，盐丘和高速的沉积层则由基网格进行划分，可以看到网格步长变化和高速区的不规则边界较为贴合，体现了自适应网格的灵活性。另外，为了避免网格变化产生的误差与正常的反射界面产生的反射波耦合，也避免细网格差分模板的部分点延伸到粗网格范围内，细网格覆盖范围略微超出了低速区，覆盖了周边的一部分高速区。为满足计算稳定性要求，设置时间步长dt=0.000 8 s。震源位于（8 905 m，0 m），4～9号检波点位于盐丘深部高速区（基网格），12 号检波点位于盐丘浅部（基网格），10、11、13和14号检波点位于地表低速区。本测试使用全局细网格（h=10 m）计算得到的波形为参考解。

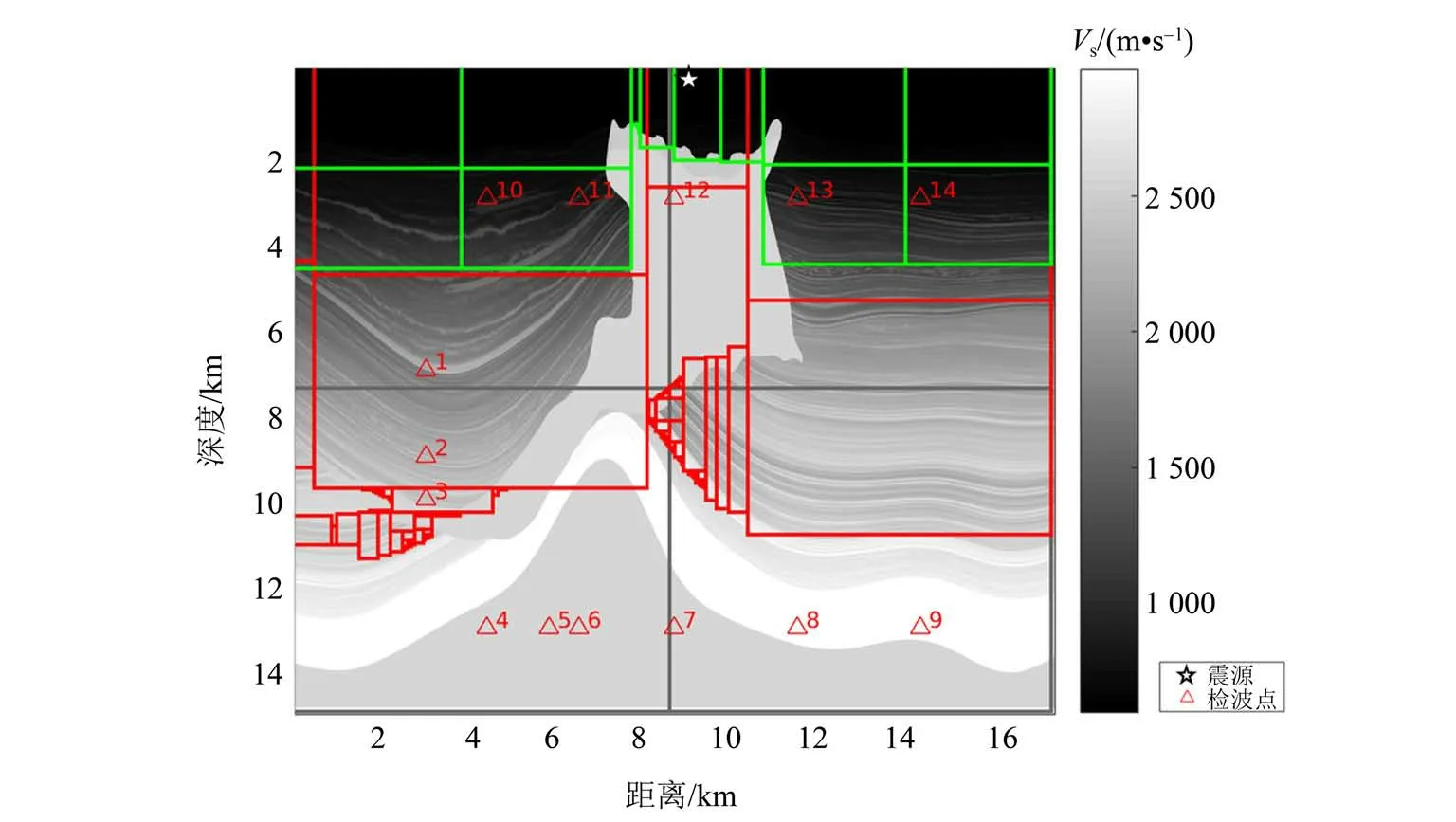
图14 SEAM模型及网格Fig.14 SEAM model and diagram of grid refinement

图15 和16 比较了接收点处（见图14）自适应网格和全局细网格计算得到的速度分量。可以看到拟合程度较高。为定量评估自适应网格的结果和参考解的拟合程度，分别计算了EM 和PM，结果见图15 和16。与其他检波点相比，5～8 号检波器vx分量的主要能量集中在记录后段，受记录后段的误差影响更大；vz分量的能量分布没有明显区别。自适应网格误差随传播过程逐渐积累，记录后段误差更大。所以5～8号检波点记录vx分量误差更大。所有检波点自适应网格和均匀细网格的波形拟合程度均可以达到“excellent”。时间效率方面，与全局细网格相比，自适应网格将需要进行计算的网格点减少到约50%，计算时间也减少到约50%。本次测试的结果证实了自适应网格模拟的准确性和高效性，以及在复杂模型地震波模拟中的适用性。

图15 1～7号检波点处（如图14）自适应网格模拟结果和参考解的比较Fig.15 Comparison of the velocity components calculated with the AMR grid and those with the uniform grid at 1-7 receivers in Fig.14

图16 SEAM模型在8～14号检波点处（如图14）自适应网格模拟结果和参考解的比较Fig.16 Comparison of the velocity components calculated with the AMR grid and those with the uniform grid at 8-14 receivers in Fig.14

5 结 论

为了降低网格在模型内高速区域的过采样，提高计算效率，我们将自适应网格和同位网格有限差分法相结合进行弹性波数值模拟。

我们采用4个模型对方法的准确性和效率进行了验证：均匀模型、层状模型、盆地模型和复杂的SEAM 模型。使用自适应网格的结果和使用全局均匀细网格的结果进行比较。基于数值实验结果得到了如下结论：

1）使用自适应网格的计算结果满足精度要求，相位误差和幅值误差在10%左右；

2）使用自适应网格计算过程中复杂的数据结构冗余较小，计算时间大致与网格点数成正比；

3）自适应网格通过降低总网格数，和通过增大高速区网格大小提高满足稳定性的时间步长，使总体计算效率提升。

此外，施加自由表面边界条件时，由于不同等级的网格点不重合，需要将地表全部用细网格覆盖。今后的研究将改进这一点，减少自由表面处不必要的细网格点。本文所述的自适应网格方案可以推广至震源动力学模拟。