考虑客户满意度的多目标多行程车辆路径优化

□刘 虹 傅晓敏

[福州大学 福州 350108]

引言

城市物流行业发展日益快速，促使物流企业竞争愈加激烈，为提高竞争优势，车辆路径作为物流配送的关键环节，必须具备更大的灵活性才能适用多变、激烈的物流市场。在城市配送系统中，货物经由车辆从城市配送中心交付至客户，考虑城市路况的局限性，一般采用小型容量车执行配送任务，同时又存在车辆更早于工作日结束前返回配送中心的情况，在Olivera和Viera[1]发现单行程车辆路径问题不适于较低车辆容量限制及配送时间较长的路径后，多行程车辆配送开始受到广泛的关注。

多行程（Multi-Trip，MT）配送由于允许车辆中途返回配送中心，可在配送中心和配送点之间多次往返完成任务[2]，在提高服务效率、降低车辆启动成本和司机雇佣费用等方面占有明显优势。随着城市经济规模扩大、新兴技术发展，研究多行程车辆路径在复杂配送环境中的优化问题，对科学规划城市配送具有重要意义。

在多行程物流中，MTVRP研究内容主要集中于分配路线数量、限制车辆服务时间、求解优化算法和调整策略等方面。Francois等学者先构造初始路径集合后单独分配给车辆，并采用大规模邻域搜索算法寻求最优解[3]；Hernandez等学者开放车辆服务时间限制，研究了带时间窗的多行程路径问题，并设计分支定价算法寻求路径最优[4]；宋强等学者在时间约束条件下构建MTVRP数学模型，并分别改进了混合遗传算法、迭代局部搜索算法和变邻域搜索算法进行求解，寻求运行成本最小化[5～7]；Ampol等学者改进了插入启发式算法求解带有时间窗、班次时间限制和可变交货时间的多行程库存路径问题[8]；学者李阳和范厚明针对客户的不确定需求，引入不确定相关理论，提出点返回多行程策略进行路径优化，研究了寻求总成本最小的MTVRP问题[9～10]；张晓楠等学者在客户模糊需求和时间窗偏好约束下，以物流成本和时间成本总和最小为目标构建MTVRP模型，并提出“基于成本期望值”的实时调整策略[11]。

综上所述，已有多行程路径问题研究文献主要集中以降低运输成本为主要目标的模型求解优化上，考虑客户满意度的多行程配送的研究较少，且多行程路径允许多次配送的特征直接影响车辆配送时间和次数，进而会导致客户满意度发生变化，加之随着物流配送的多样化，客户满意度将作为企业提高核心竞争力的一个关键，因此研究考虑客户满意度的多行程车辆路径优化具有实际意义。根据多行程的特点，本文从配送时间窗、服务次数两方面衡量客户满意度并建立相应的客户满意度函数，同时兼顾客户取送双向随机需求，构建同时考虑运输成本和满意度的多目标多行程路径优化模型，并设计求解算法寻求最佳车辆配送路径决策。

一、问题描述及模型建立

（一）问题描述与假设

本文研究的是包含配送中心和客户点的配送网络中的多行程车辆路径问题。货物在配送中心进行集中送货，客户为同时取送货及其需求具有随机性，配送中心派遣车辆采用同时取送的多行程配送模式服务客户点。客户根据货物送达时间的不同会产生不同程度的满意度，客户接受车辆服务次数的不同也会影响满意度，多行程车辆配送需进行路径决策，使得客户满意度最大和运输成本最小。

为突出多行程配送的特性，做出如下假设：

1. 配送中心的坐标以及客户点数量、坐标、配送时间窗、服务次数要求已知；

2. 客户取送货需求均服从随机分布，且只有当车辆到达客户点时其需求才会被确认；

3. 每辆车仅有一条配送路线，且每条路线上的客户取送货需求总量不能超过车辆容量能力；

4. 取送货物可以进行混合运输，车辆从配送中心出发，完成配送任务之后需要返回配送中心；

5. 配送途中匀速行驶且速度已知，配送途中的运输成本只与配送路程相关；

6. 预优化中每个客户点仅能接受一辆车服务，且车辆首次从配送中心出发时均处于满载状态；

7. 实际配送中可采用部分服务策略，即客户允许同一辆车多次配送。

（二）符号和变量说明

1. 参数符号

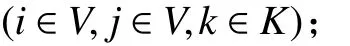
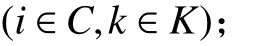
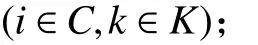
TB：车辆k在配送中心处的补货时间；

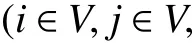
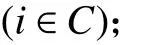
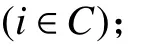
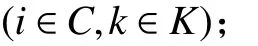
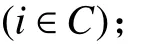
2. 决策变量

（三）满意度测度

在多行程配送活动中，客户具有自己的期望配送时间窗和服务次数要求，为兼顾客户的服务需求，考虑客户对车辆到达时间和实际配送次数的不同心理感受，分别建立客户满意度测度函数，综合衡量客户服务水平。

1. 时间窗满意度函数

定义1比较车辆到达客户时刻与客户配送时间窗以背离配送时间窗程度衡量客户满意度，见图1，客户满意度函数表达式详见式（1）。

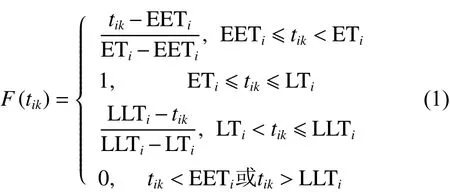
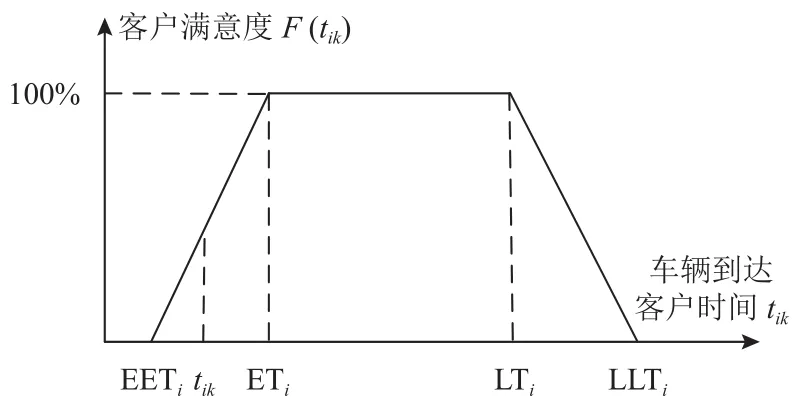
图 1 时间窗满意度函数

不同时间区间的满意度如下：

2. 服务次数满意度函数

定义2服务次数与客户满意度呈负相关，服务次数越多，客户满意度越低，比较车辆实际配送次数与客户服务次数范围，对客户满意度函数描述详见式（2）。

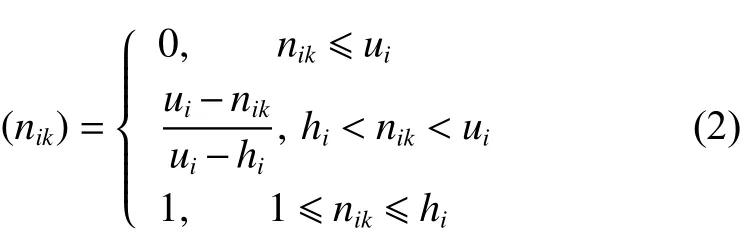
不同次数区间的满意度如下：

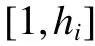
3. 客户综合满意度函数

定义3客户综合满意度由基于配送时间窗的满意度式（1）和基于服务次数的满意度式（2）共同决定，客户综合满意度函数表现为式（3）。

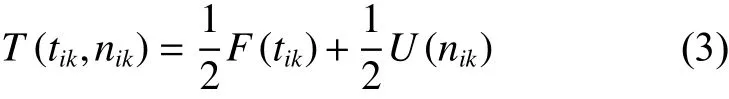
（四）数学模型

1. 目标函数

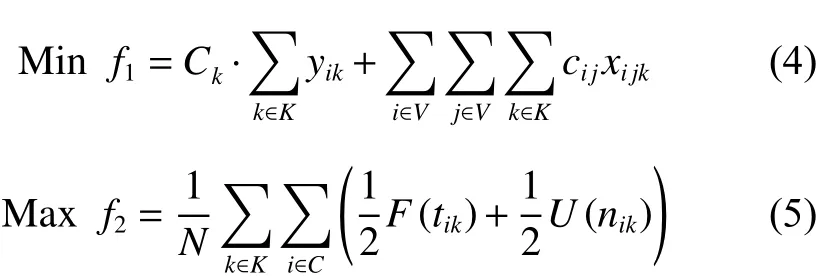
2. 约束条件

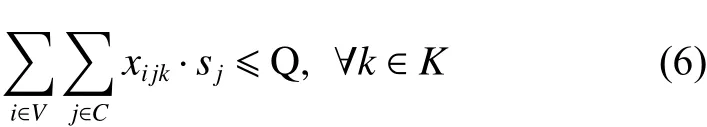
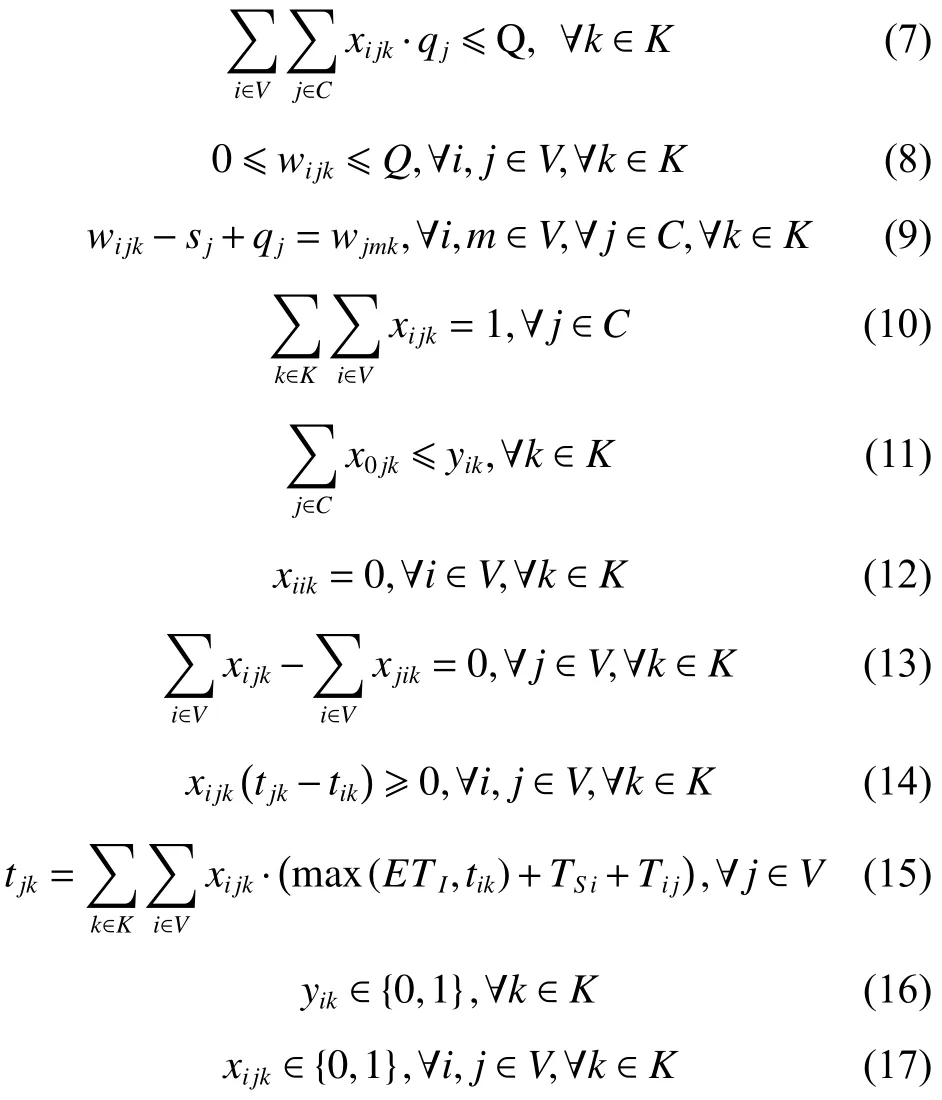
其中，式（4）和（5）为目标函数，式（4）为最小化车辆派遣成本和配送成本之和；式（5）为最大化客户平均满意度，包括时间窗满意度和服务次数满意度；式（6）表示配送路线上需求点的正向配送总量小于等于车辆载重限制；式（7）表示配送路线上需求点的逆向揽收总量小于等于车辆载重限制；式（8）表示车辆在配送途中的负载量不超过车辆最大载重限制；式（9）为车辆在服务客户点j后的动态负载量的计算等式；式（10）～（11）保证预阶段路径方案中任一客户点有且仅有一条车辆配送路线，且车辆只能从配送中心出发一次；式（12）～（13）消除不合理回路，且保证同一个客户点之间没有车辆配送路线；式（14）表示车辆配送时间先后要与客户配送顺序一致；式（15）为车辆配送客户前后的时间计算式；式（16）～（17）表明决策变量属性。

二、模型转换与求解

（一）随机机会约束规划模型

1. 目标函数

同目标函数式（4）～（5）。

2. 约束条件

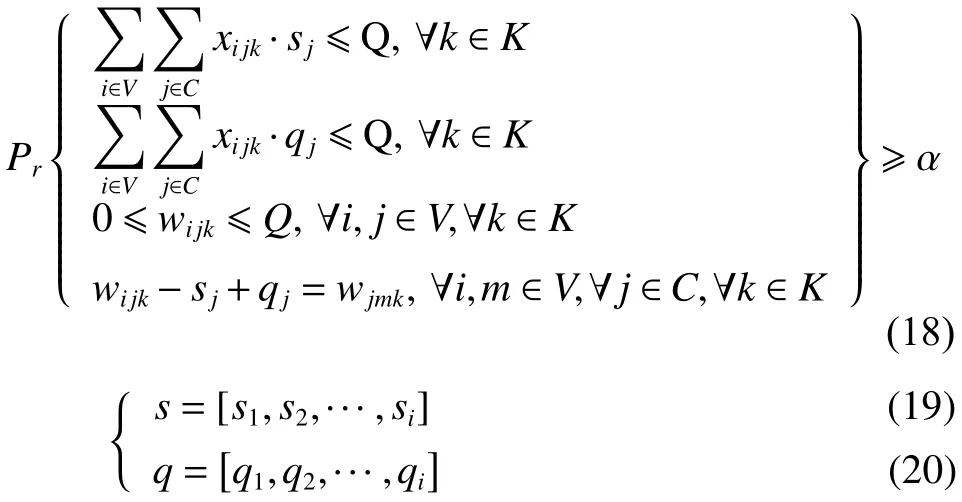
其余约束同式（10）～（17）。

（二）点判断实时策略

定理1车辆服务下一客户点，拟选择方案一，则客户点的成本期望值和满意度期望值详见如下：

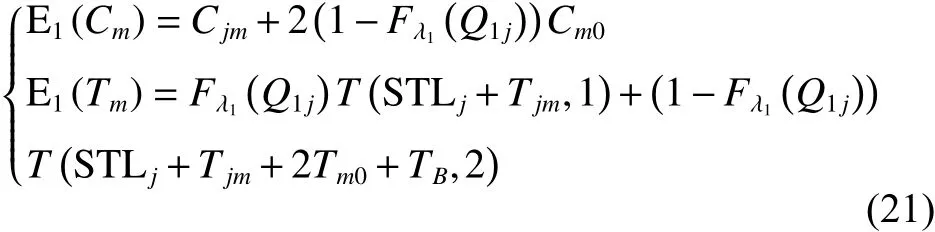
证明：

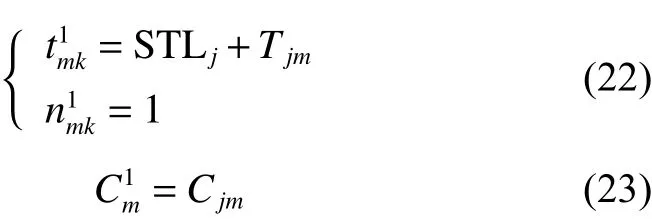
由将式（24）代入式（3）得

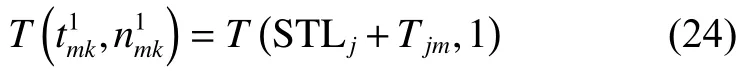
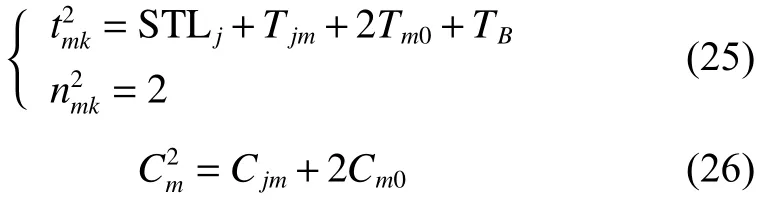
由将式（25）代入式（3）得

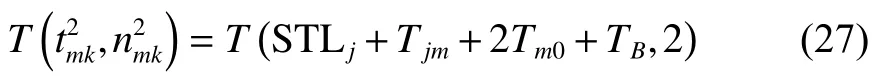
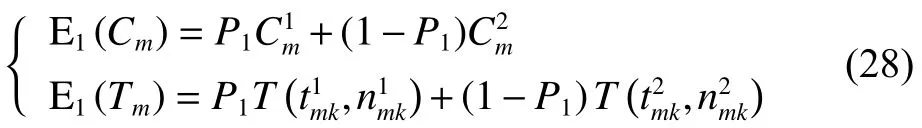
将式（25）～（26）、式（28）～（29）、式（31）代入式（30）可得式（23），至此式（23）得证。

定理2车辆服务下一客户点，拟选择方案二，则客户点的成本期望值和满意度期望值详见如下：

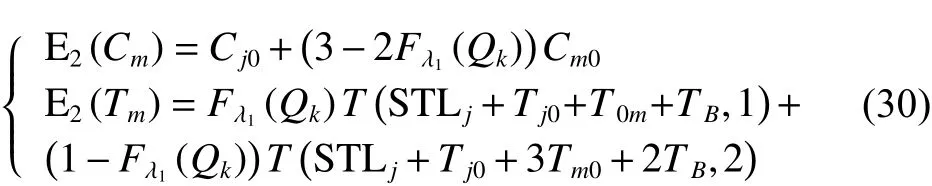
证明：

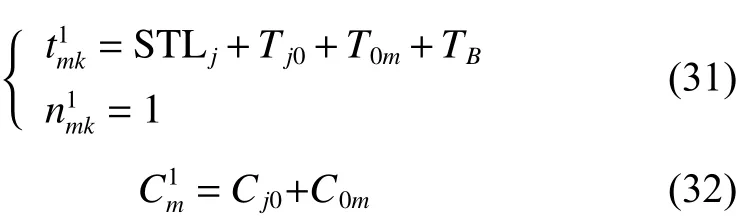
由将式（34）代入式（3）得

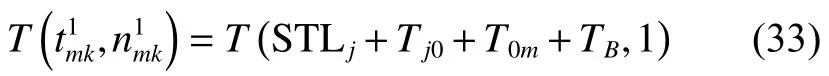
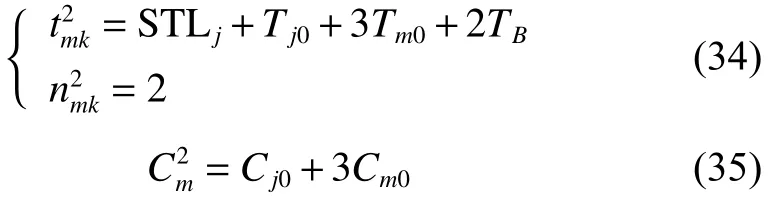
由将式（37）代入式（3）得

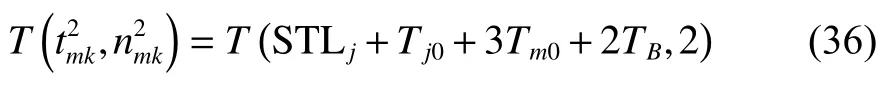
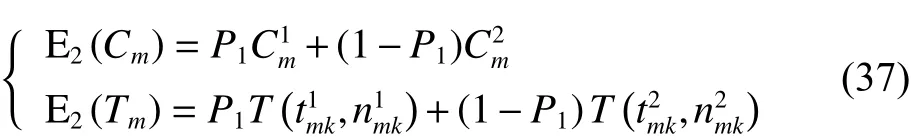
将式（34）～（35）、式（37）～（38）、式（40）代入式（39）可得式（32），至此式（32）得证。

针对不同方案下得到的客户点期望值结果，选择配送成本期望值较小且客户满意度较高的方案作为车辆在服务客户点之后的路径优化选择。

（三）模型求解

多行程车辆路径问题属于NP难题，考虑多目标优化的MTVRP模型求解难度增加，禁忌搜索算法可通过使用禁忌规则使算法跳出局部迂回，实现全局最优化[14～15]，故本文针对多目标优化模型，设计了嵌套调整策略的灰关联分析多目标禁忌搜索算法进行求解。

1. 灰关联分析

灰关联分析主要通过灰关联度判断序列间关联程度。确定一个序列作为参考标准，然后将其他序列与参考序列进行比较，与参考序列越接近，表示该序列效果越好，反之则表示效果越差。基于传统灰色关联分析，引入信息熵理论，用均衡接近度代替灰关联度，有效弥补了关联倾向的缺陷[16～17]。

灰关联分析的具体步骤如下：

2. 嵌套调整策略的灰关联分析多目标禁忌搜索算法

针对MTVRP多目标优化模型设计的算法如下：

Step 9：生成最终解。通过点判断实时策略进行多行程路径调整，生成实际路径决策，输出最终解。

三、算例验证与结果分析

（一）实验算例

本文研究的考虑客户满意度的同时取送货多行程车辆路径问题模型，尚无标准测试算例，针对所建模型特点，参考Prodhon的选址-路径问题标准算例集50-5-1，进行适当选取和扩展得到本文测试算例。设客户点送货需求和取货需求分别服从为50和35的泊松分布，参考文献[18]增加时间窗限制，具体数据如表1所示。此外，配送中心坐标为（43,3），车辆派遣成本=2 500，单位配送成本=25，车容量能力=220，客户点服务时间=10，补货时间=10，车辆速度=1。由于本文的多行程配送方式，对于参数、需根据配送中客户对服务次数的接受程度来设定，本实验设定参数= 1，=3来测试算例。

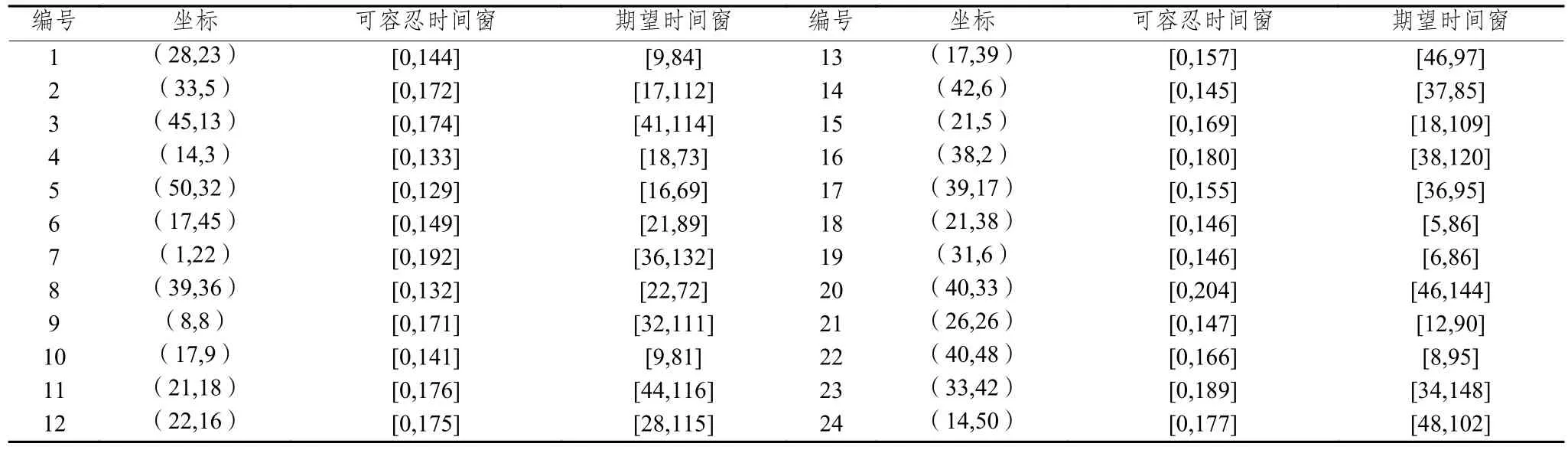
表 1 客户节点坐标及配送时间窗数据

（二）实验结果与分析

1. 预先优化阶段

对算例进行仿真实验，得到的Pareto解集结果如表2所示。为了更好分析，通过客户满意度公式，计算以运输成本为单目标求得最优解对应的客户满意度为86.87%，并将其标注于Pareto解集坐标图上，如图2所示。

从空间分布对比图中可以看出：只关注成本的单目标多行程路径模型在配送成本上取得了比同时考虑成本和客户满意度的多目标多行程路径模型的所有决策方案都更好的表现。然而在客户满意度上的表现均劣于多目标多行程路径模型的所有方案。由此可见，运输成本和服务水平两个目标是不能同时达到最优，追求低成本需要以降低客户满意度为代价，提高满意度通常也会增加物流成本。企业可根据自身发展需求选择合适的决策方案。

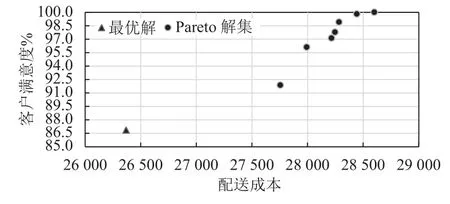
图 2 单目标最优解与Pareto解集空间图

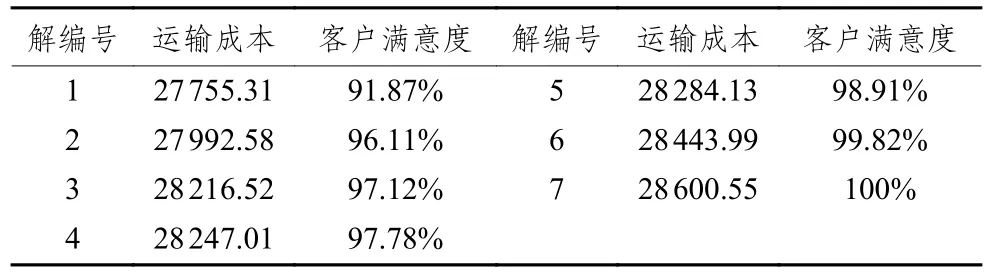
表 2 Pareto解集

针对模型求解所得的Pareto解集所对应的方案很难进行优劣之分，但决策者总是需要从中选择一个用以指导路径规划。本文分别将运输成本、客户满意度作为单目标进行优化，仿真15次求得最优解26 368、1（作为灰关联参考序列），通过计算并比较Pareto解集所对应的目标函数值序列与参考序列（26 368，1）的均衡接近度，确定最优方案，为企业提供最佳参考。Pareto解集对应的均衡接近度如表3所示。

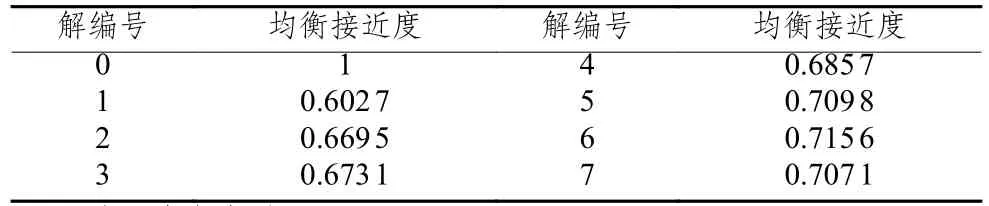
表 3 Pareto解集均衡接近度

由表3可知，Pareto解6与最优解（26 368,1）的均衡接近度为0.715 6最大，根据灰关联分析理论可知，均衡接近度越大，表明Pareto解6越接近理想最优解。由此，选择Pareto解6作为预优化阶段最佳参考解，具体决策方案为车辆1：0-6-24-7-11-0，车辆2：0-8-23-22-20-0，车辆3：0-19-9-1-2-0，车辆4：0-4-10-15-12-0，车辆5：0-5-17-14-16-0，车辆6：0-21-13-18-3-0，总成本为28 443.99，客户满意度为99.82%。

2. 实际配送阶段

（1）实际配送中，在没有采取任何实时策略的前提下，车辆按预优化阶段参考路径服务客户，由于取送货需求的随机性，车辆的剩余载货量或者空余可载货量可能不足导致客户点配送失败，造成配送路径的中断，具体情况如图3所示。在路线1中，客户11为配送失败的中断点，致使客户点11前后相邻路径为无效配送路径；在路线4中，客户4为中断点，客户4作为车辆服务首个客户点，导致整个车辆服务路线4为无效路径；在路线5中，客户16为配送失败的中断点，因此客户点16前后相邻配送路径无效。

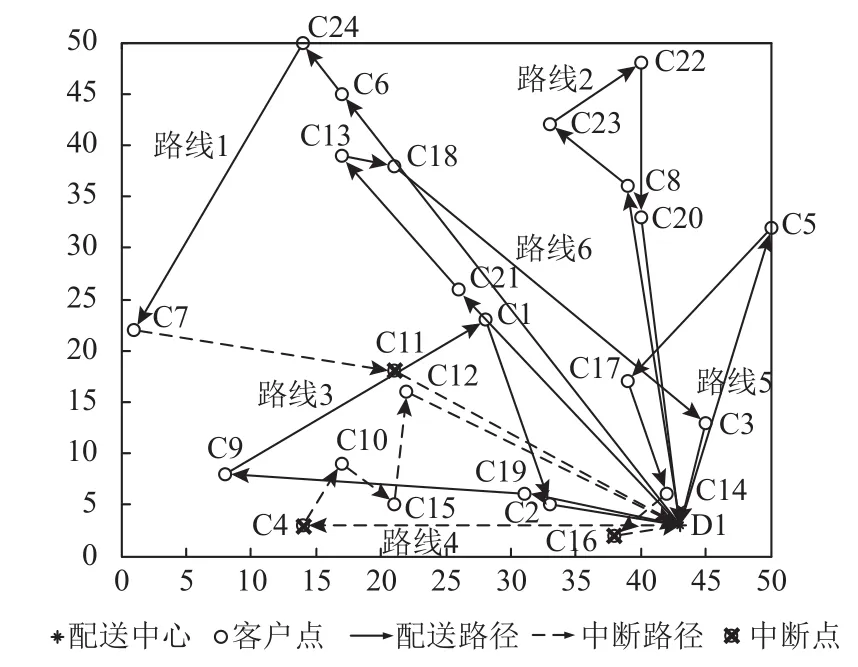
图 3 配送中断路径图

（2）在实际配送中，采取本文提出的“点判断”多行程策略进行实时路径调整，实际配送路径方案为车辆1：0-6-24-7-0-11-0，车辆2：0-8-23-22-20-0，车辆3：0-19-9-1-2-0，车辆4：0-4-0-4-10-15-12-0，车辆5：0-5-17-14-0-16-0，车辆6：0-21-13-18-3-0，总成本为31 838，客户满意度为92.15%。“点判断”实时调整策略基于预先优化最佳路径方案进行调整，较于无任何调整策略下实际配送产生中断，可避免因客户需求随机导致路径中断。

四、结论

在多行程配送网络中，综合考虑客户满意度和运输成本建立多行程路径多目标优化模型，针对模型具有同时取送、随机参数、多行程动态以及多目标等特征，提出“点判断”实时调整策略，引入随机机会约束规则和灰关联分析理论，设计了嵌套调整策略的灰关联多目标禁忌搜索算法寻求最佳配送路径。通过算例实验，验证了模型和算法的有效性。得出以下结论：

1. 低成本运输是物流企业追求的长期目标，而随着物流行业间竞争的愈发激烈，服务水平将成为企业提高核心竞争力的一个关键。多行程路径配送模型同时考虑成本和客户满意度进行多目标优化，可为企业如何同时兼顾物流成本和服务水平提供参考。

2. 采用“点判断”实时策略调整进行多行程配送，可有效避免配送路径中断，同时多行程配送会产生基于服务次数的客户满意度，符合实际情境。

3. 用灰关联分析理论和禁忌搜索算法相结合，能有效寻求路径最优，提高算法求解质量。

在多方因素的影响下，现实中的多行程配送网络较为复杂，进一步研究多行程配送系统中的多动态模型将是下一步的研究重点。