NUMERICAL DYNAMICS OF NONSTANDARD FINITE DIFFERENCE METHOD FOR MACKEY-GLASS SYSTEM
YAO Jie-yi,WANG Qi
(School of Mathematics and Statistics,Guangdong University of Technology,Guangzhou 510006,China)
Abstract:This paper deals with the numerical dynamics for Mackey-Glass system.By using the nonstandard finite difference method and bifurcation theory of discrete systems,we prove that a series of Hopf bifurcation appear at the positive fixed point with the increase of time delay.At the same time,the parameter conditions for the existence of Hopf bifurcations at positive equilibrium point are given.Finally,we provide some numerical examples to illustrate the effectiveness of our results.The nonstandard finite difference method is easy to construct and has less computation.It is suitable for the bifurcation analysis of nonlinear systems and extends the results in the literature.
Keywords: nonstandard finite difference method;Mackey-Glass system;Hopf bifurcation;stability
1 Introduction
Delay differential equations are close to reality and reveal complex life phenomena.Due to the increase of time delay,the topological structure of differential equations may change qualitatively,and some properties of the system,such as equilibrium state,stability and periodic phenomenon will change suddenly,that is the so-called bifurcation phenomenon.In the past half century,many scholars began to pay attention to the research of bifurcation theory of delay differential equations and obtained lots of meaningful achievements[1–5].
In practical application,it is very important to study the bifurcation problem by numerical method that the continuous time model is usually discretized for the purpose of experiment or calculation.If both the discrete-time model and the continuous model exhibit similar dynamic behaviors,such as the steady-state stability behavior and persistence of the solution,the boundedness,chaos and bifurcation,then we say it is dynamically consistent[6–8].In order to reproduce the dynamic behavior accurately,some dynamic consistent numerical methods are needed.In 2015,Jiang et al.[9]studied the Hopf bifurcation for a kind of discrete Gause-type predator-prey system with time delay,which is obtained by Euler method.They gave some parameter conditions for the existence of a unique positive fixed point,and obtained the stability result of the positive fixed point.In 2020,Euler approximation is implemented to obtain discrete version of Schnakenberg model by Din and Haider[10].They also proved that discrete-time system via Euler approximation undergoes Hopf bifurcation as well as period-doubling bifurcation was also examined at its unique positive steady-state.Moreover,they proposed a nonstandard finite difference method(NSFDM)for Schnakenberg model and proved that NSFDM could preserve the corresponding dynamic behavior.Using time delay τ as a parameter,Ding et al.[11]studied the dynamics of Mackey-Glass system by using trapezoidal method,and proved that with the increase of delay,the positive equilibrium point lost stability and Hopf bifurcation occured.
Compared with the Euler method,the NSFDM becomes an effective tool for nonlinear dynamic system based on its good dynamic consistency and good accuracy[12,13].Compared with the trapezoidal method,the NSFDM is less of computation.In this paper,we propose a NSFDM for Mackey-Glass system such that it can preserve its dynamic properties.
For the following nonlinear delay differential equations
which was described by Mackey and Glass[14]as physiological control systems in 1977,where β,θ,n and γ are all positive constants,p(t)is the density of mature cells in blood circulation,τ is the time delay from immature cells in bone marrow to maturation and release in circulating blood.For more information on this model,the interested reader can refer to[15].Throughout this paper,we suppose that

If the condition

is satisfied,then every positive solution of(1.1)oscillates about its positive equilibrium point[16].Whether(1.1)is sustained for oscillations and stability arouses our great interest.Symptoms of chronic granulocytic leukemia(CGL)can be described by this model.For normal adults,the circulating granulocyte density is either stable or there is a small vibration.This vibration period is generally between 14 and 24 days.The vibration period is about 21 days,which is a change from health to sub-health.In the 30-70 days of the cycle,the density of granulocytes will appear large vibration,that is unhealthy phenomenon,the disease of CGL.In this paper,we focus on the stability and Hopf bifurcation of discrete scheme of(1.1).The effect of time delay on the dynamic behavior of the system is studied,and the conditions for the generation of Hopf bifurcation are also given.
2 The Stability of the Positive Equilibrium and Local Hopf Bifurcation
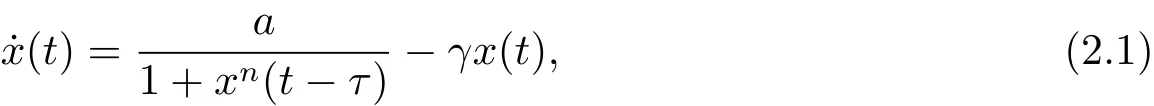
let u(t)=x(τt),then(2.1)becomes

Under transformation p(t)=θx(t),(1.1)changes into
here a= β/θ.In classical FDM,the first derivative du/dt is replaced by(u(t+h)-u(t))/h,where h is the step size,however,du/dt is replaced by(u(t+h)-u(t))/φ(h)in NSFDM,where φ(h)called denominator function,is the continuous function of step size h,which satisfies φ(h)=h+O(h2),0< φ(h)< 1,h → 0.
In this paper,we select the denominator function of NSFDM which is φ(h)=(1-e-aτh)/(aτ),where h=1/m is the step size.Using the NSFDM to(2.2),we obtain the following difference scheme
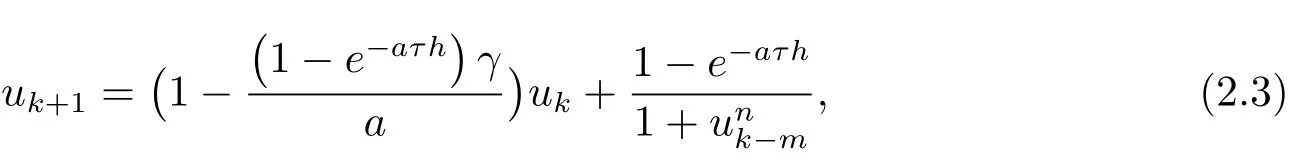
here ukand uk-mare the approximate values to u(tk)and u(tk-τ),respectively.
It is obvious that(2.2)and(2.3)have the same fixed point u*,which satisfies γun+1+γu-a=0.Let F(x)= γxn+1+ γx-a,then F′(x)=(n+1)γxn+ γ > 0 for x ≥ 0.Therefore,(2.2)has a unique positive fixed point u*.At the same time,a/(1+un*)-γu*=0 implies that

Set yk=uk-u*,then yksatisfies
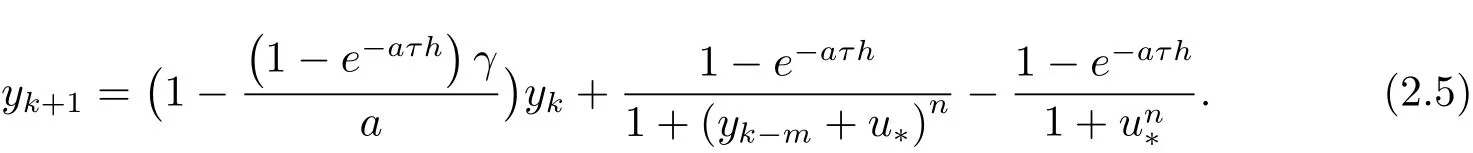
Let Yn=(yn,yn-1,···,yn-m)T,we introduce a map Yn+1=F(Yn,τ),where F=(F0,F1,···,Fm)Tand

Obviously,the origin is a fixed point of Yn+1=F(Yn,τ),and its linear part is Yk+1=AYk,where
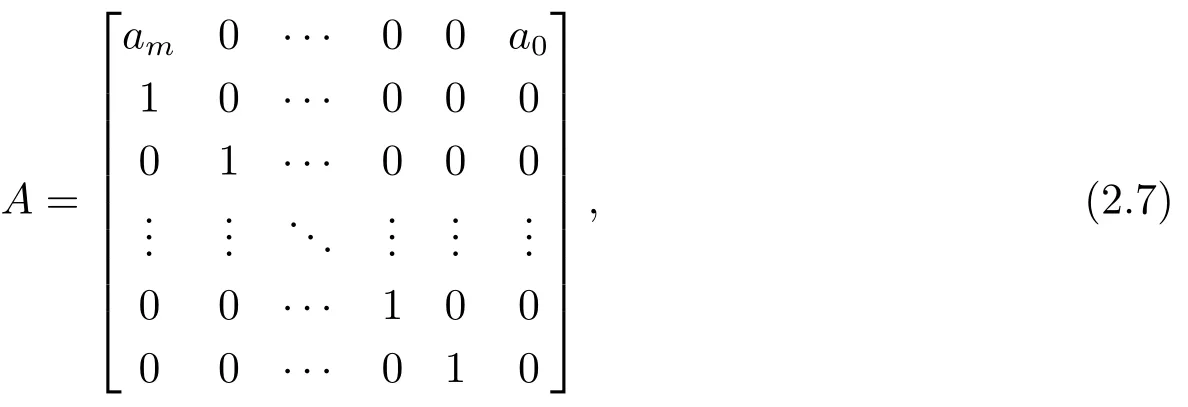
and

Therefore,the characteristic equation of A is

Lemma 2.1For sufficiently small τ> 0,all roots of(2.9)are less than one.
ProofWhen τ=0,(2.9)is equivalent to λm+1- λm=0.It has an m-fold root zero and a single root λ =1.Considering the root λ(τ)of(2.9),making λ(0)=1,this root depends continuously on τ and(2.9)is differentiable about τ,then we have
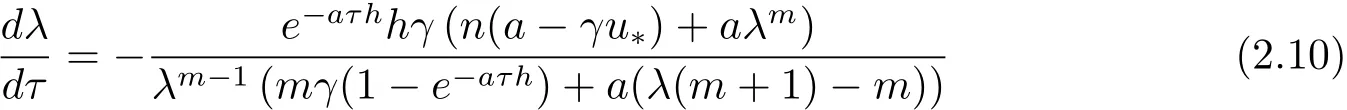
and

Since

from(2.4)and(2.12),we obtain that

So λ can not go through unit circle.Therefore,for sufficiently small τ> 0,all characteristic roots of(2.9)are within the unit circle.
Suppose eiωis a root on the unit circle,when ω ∈ (0,π],eiωis the root of(2.9),so we have

Separating the real part and the imaginary part from(2.14),we give
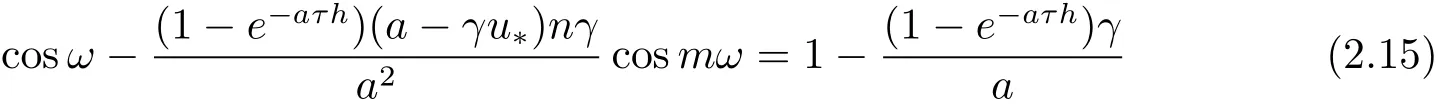
and

So we obtain

If n(a-γu*)/a<1,then cosω>1,which is a conflict,so the lemma is proved.
Lemma 2.2Supposing that n(a-γu*)/a< 1,(2.9)has no modules of roots more than one.
From(2.16),we get that
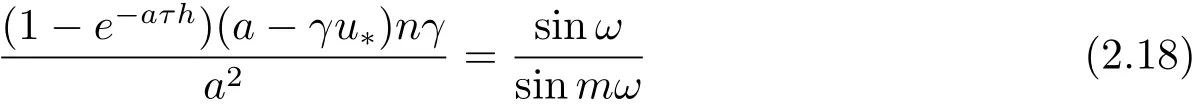
is positive,sinω has the same symbol as sinmω.So there exists a real sequence ωiwhich satisfies
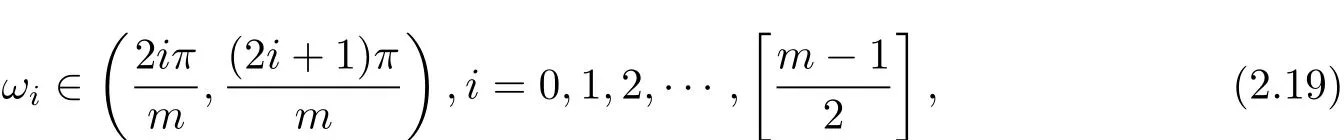
where[.]is the greatest integer function.
Lemma 2.3Suppose that n(a-γu*)/a>1,then

ProofFrom(2.8)and(2.9),we have

Then by(2.10)and(2.21),we obtain
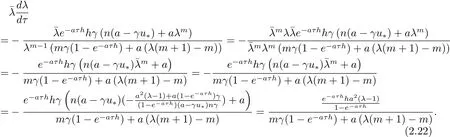
From(1.2)we get

Lemma 2.4
(i)If n(a-γu*)/a < 1,then for any τ> 0,all roots of(2.9)are in the unit circle.
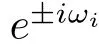
ProofBy Lemma 2.1,Lemma 2.2 and Corollary 2.4 in[17],we can obtain(i).
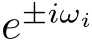
From Lemma 2.4,the stability of the zero solution can be obtained in the following theorem.
Theorem 2.5
(i)If n(a-γu*)/a < 1,then u=u*is asymptotically stable for any τ≥ 0.
(ii)If n(a-γu*)/a > 1,then u=u*is asymptotically stable for τ∈ [0,τ0),and unstable for τ> τ0.
(iii)For n(a- γu*)/a > 1,(2.5)undergoes a Hopf bifurcation at u*when τ= τi,for i=0,1,2,···,[(m-1)/2].
3 Numerical Simulations
Let a=2,γ=1 and n=4 in(2.2),it is easy to find that the positive equilibrium point u*=1,so the condition n(a-γu*)/a>1 holds.
In Table 1,we give the absolute errors(AE)and the relative errors(RE)at t=10 of the NSFDM with initial value u(t)=1.1 and τ=1.From this table we know that the NSFDM has good convergence.

Table 1 The errors of NSFDM
In Table 2,we give the values of τkfor different step size h=1/2,1/4,1/8 and 1/16.From Theorem 2.5 and Table 2 we can see that τkis the bifurcation points.Furthermore,in Figures 1-4,we present the numerical solution and phase diagram of the system discretized by the NSFDM.From Theorem 2.5 we can conclude that the equilibrium is asymptotically stable for τ∈ [0,τ0)(τ0≈ 1.0986 in Figure 1,τ0≈ 0.7643 in Figure 2,τ0≈ 0.6734 in Figure 3 and τ0≈ 0.6368 in Figure 4),unstable for τ> τ0and an attracting bifurcating periodic solution exists for τ> τ0.This is just what Figures 1-4 show intuitively.
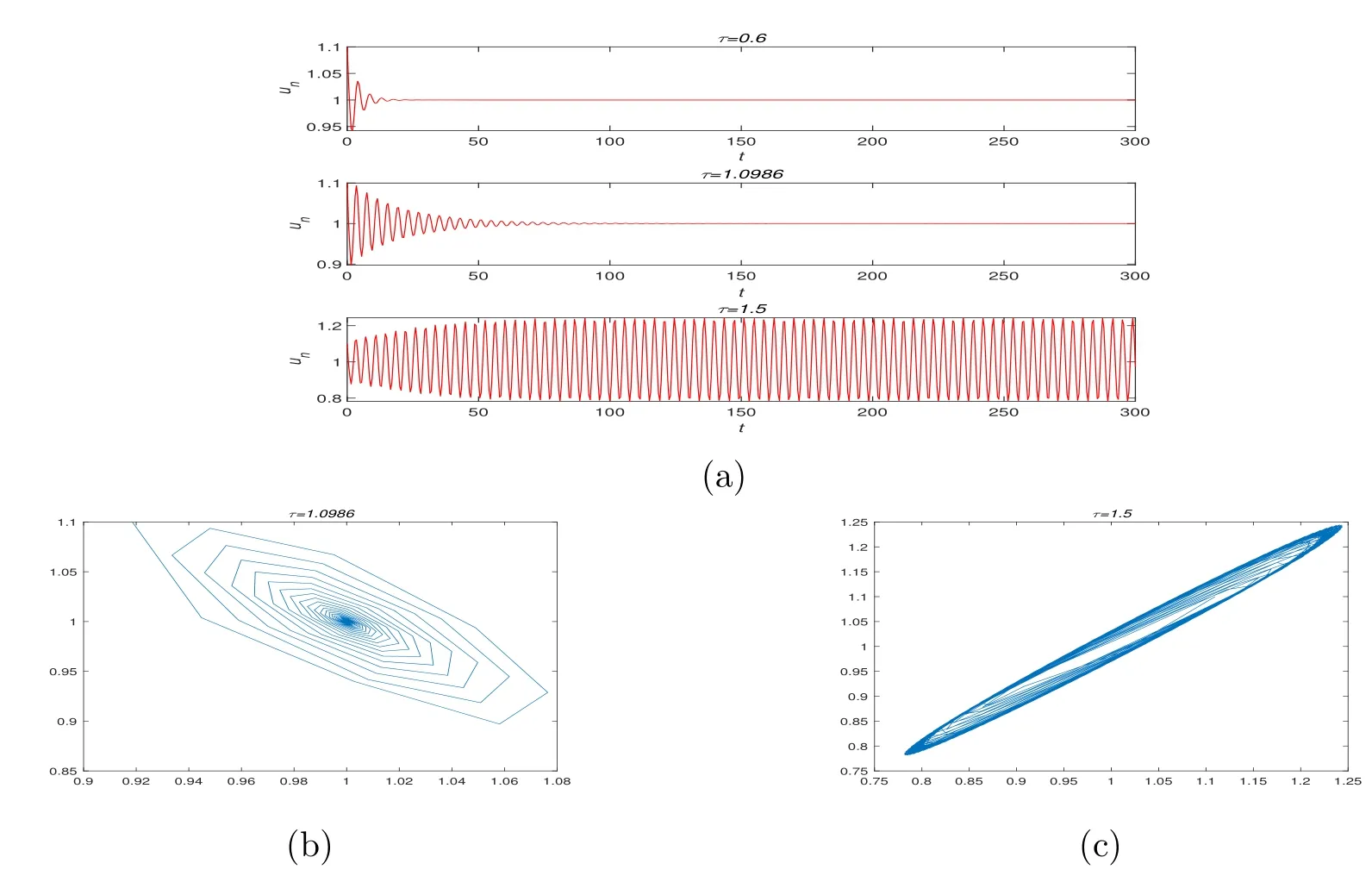
Figure 1 Numerical solution and phase diagram with step size h=1/2.(a)numerical solution;(b)phase diagram for τ=1.0986;(c)phase diagram for τ=1.5.

Figure 2 Numerical solution and phase diagram with step size h=1/4.(a)numerical solution;(b)phase diagram for τ=0.7643;(c)phase diagram for τ=1.5.

Figure 3 Numerical solution and phase diagram with step size h=1/8.(a)numerical solution;(b)phase diagram for τ=0.6734;(c)phase diagram for τ=1.5.

Figure 4 Numerical solution and phase diagram with step size h=1/16.(a)numerical solution;(b)phase diagram for τ=0.6368;(c)phase diagram for τ=1.5.

Table 2 The values of τk
It is not difficult to see that the given numerical results illustrate the correctness of the theoretical analysis.
4 Conclusion
Mackey-Glass system is discretized by NSFDM,the influence of time delay on blood cell density is analyzed.If the time delay exceeds a certain critical value,Hopf bifurcation will occur and result in the density of mature cells produce periodic oscillation.However,if the delay is small enough,the equilibrium is stable.
From a biological point of view,if we can put off the production of immature cells in bone marrow to the normal time of their release in the circulating blood,stabilize the density of mature cells in the blood circulation,the disease will be brought under control.Our analysis results can provide critical insights and guidance for the analysis and design of control schemes from the perspective of dynamics and control theory.
- 数学杂志的其它文章
- RESEARCH ANNOUNCEMENTS ON“MODERATE DEVIATIONS FOR GRENANDER ESTIMATOR NEARBOUNDARIES OF THE SUPPORT”
- ON REFINED YOUNG’S REVERSE INEQUALITIES FOR POSITIVE LINEAR OPERATORS
- SYMPLECTIC CRITICAL SURFACES WITH CIRCULAR ELLIPSE OF CURVATURE IN TWO-DIMENSIONAL COMPLEX SPACE FORMS
- STUDY ON 2-DIMENSIONAL SUBMANIFOLDS WITH CONSTANT DETERMINANT OF BLASCHKE TENSOR
- THE SPREADING SPEED FOR A NONLOCAL DIFFUSIVE PREDATOR-PREY MODEL WITH ONE PREDATOR AND TWO PREYS
- ON SPLIT REGULAR BIHOM-LIE COLOR ALGEBRAS

