两种不同脉冲欺骗攻击下随机多智能体系统的均方拟一致性
曾梓贤,彭世国,黄昱嘉,谷志华,冯万典
(广东工业大学 自动化学院,广东 广州 510006)
随着网络技术的不断发展,多智能体系统一致性问题深受学者的关注[1-2],并逐渐被应用到实际生活中,如无人机编队、电网能源分配等[3-4]。在实际应用中,多智能体系统难免会遭受到如随机干扰、网络攻击等外部因素的干扰,而这对其一致性有重要影响[4-5]。
一般地,随机干扰对多智能体系统的影响主要反映在系统动态特性或信息传输的信道中。前者可表现为随机噪声和随机出现不确定项等干扰,如文献[6]通过设计新颖的脉冲控制协议,并基于广义伊藤公式与李雅普诺夫稳定性理论得到了系统实现均方一致性的充分条件;文献[7]研究了一类具有随机出现不确定项的非线性多智能体系统的均方一致性问题。后者则一般体现在信息丢包和信道堵塞的建模中[8]。
另一方面,考虑到多智能体系统应用中环境的复杂性及其通信网络的开放性,由网络攻击所引起的网络安全问题也不容忽视。由文献[9-11]可知,攻击会导致多智能体一致性性能达不到理想的要求,并可能进一步导致智能体间的通信瘫痪。一般地,网络攻击主要分为两大类:拒绝服务性攻击和欺骗攻击[12]。在文献[13]中,作者指出在一般情况下,拒绝服务性攻击的目标可以是传感器、控制器或智能体间的传输数据,从而导致信号在传输过程中发生数据丢包或延时的问题。相比之下,欺骗攻击则可能会绕过系统的检测技术并进入系统内部,进而操控控制指令或篡改传输数据,致使系统性能下降甚至变得不稳定[14]。
欺骗攻击可进一步分为虚假数据注入攻击和替代欺骗攻击等类型。虚假数据注入攻击主要是向控制器加入错误数据来破坏系统数据的完整性和准确性,如文献[15]将虚假数据引起的偏差加入到系统中来得到攻击下的系统动力学方程;文献[16]考虑了在传感器的数据传输通道中注入虚假数据情况下非线性多智能体系统一致性问题;文献[17]引入了伯努利变量来描述控制信号是否会受到虚假数据欺骗攻击。替代欺骗攻击则是指控制器受到攻击后会使控制信号被替代为相应的攻击信号,已有的关于欺骗攻击下的多智能体系统一致性的研究主要集中在传感器到控制器信道上的加性攻击,很少考虑替代攻击,文献[3]考虑替代攻击下利普希兹型非线性系统的一致性问题。值得注意的是,目前文献仅仅考虑虚假数据注入攻击或替代攻击[17-19],而同时考虑两者对一致性问题的影响则还未得到相应的研究。如何设计两种攻击下控制器的模型以及如何进一步得到系统实现一致性的条件是一个待解决的问题。
基于上述分析,本文主要研究了一类领导跟随随机多智能体系统在受到两种不同脉冲欺骗攻击情况下实现均方拟一致性问题。利用李雅普诺夫稳定性理论,本文给出了系统实现均方拟一致性的充分条件及相应的误差上界。
本文主要创新点如下:建立了同时受到两种脉冲欺骗攻击和随机噪声干扰下系统的模型;引入服从伯努利分布的随机变量来解决攻击类型的描述及其攻击成功与否的问题。
1 问题描述与预备知识
1.1 图论
在多智能体系统中,智能体之间可以相互传递数据,而图论则是能够较好地描述上述关系的工具。一般地,一个图可表示为,其中V,E 和分别表示图G的节点集、边集与连接矩阵,其中,N是一个正整数。图中节点表示智能体,边则表示智能体间传递数据的关系,连接矩阵为反映智能体间的邻接权重矩阵。假设图为无向图,包括N个跟随者和一个领导者,则有。若智能体i与智能体j间可传递数据,则节点间存在的一条边(i,j)∈。若边(i,j)∈,则有aij=aji>0,否则,aij=0。此外,假设aii=0。图的拉普拉斯矩阵表示为,且有。令,表示智能体i的邻居节点集。图中领导者的标签用0表示。领导者与跟随者间的连接关系可由矩阵C所反映,其中C=diag{c1,c2,···,cN}是一个对角矩阵。若节点间存在的一条边,则有ci=1,否则ci=0。此外,定义H=[hij]N×N=+C,则有hii=lii+ci与hij=lij,i≠j。
1.2 问题描述及协议设计
考虑一类含有N个跟随者的多智能体系统,其中各跟随者的动力学特性描述如式(1)所示。

式中:N={1,2,···,N}是一个有限集,xi(t)∈Rn与分别表示智能体i的状态变量与控制输入,其中,Rn是n维欧几里得空间;函数f:R×Rn→Rn表示智能体i的非线性特性,其中,R=(−∞,+∞)表示一个实数集;函数:R×Rn→Rn×m为噪声强度函数;ω(t)∈Rm是定义在概率空间(Ω,F,Pr)上的m维维纳过程,且ωi(t)与ωj(t),i≠j相互独立;A是 已知合适维数的常数矩阵;随机变量p(t)服从伯努利分布,与ω(t)相互独立且满足
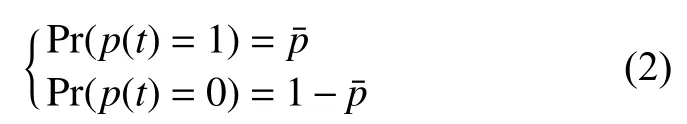
另一方面,领导者智能体的状态量假设为x0(t)∈Rn,其动力学特性描述为
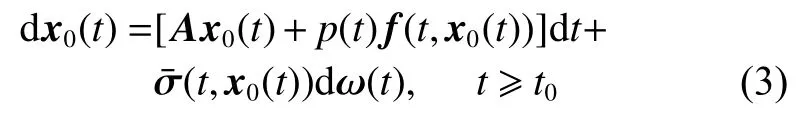
考虑控制协议同时遭受两种脉冲欺骗攻击即虚假数据注入脉冲攻击和替代脉冲攻击的影响。此外,引入两个伯努利随机变量来分别描述两种欺骗攻击成功与否。具体脉冲控制协议设计如式(4)所示。
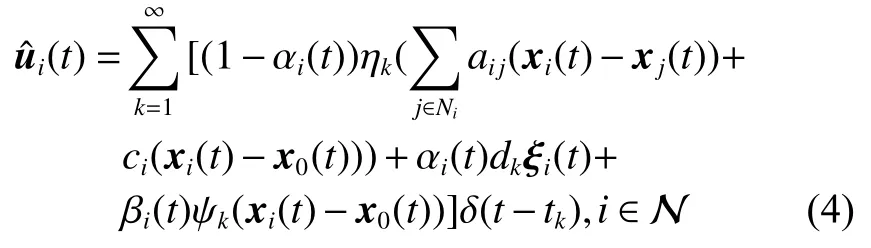
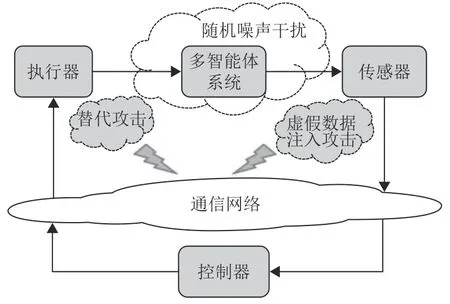
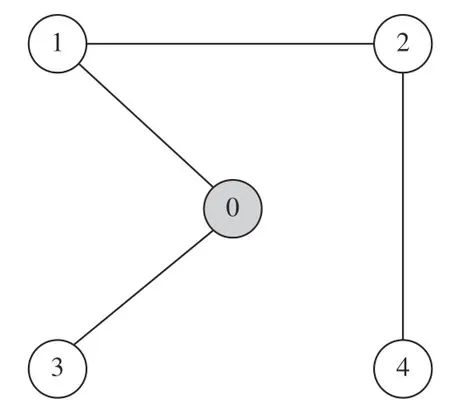
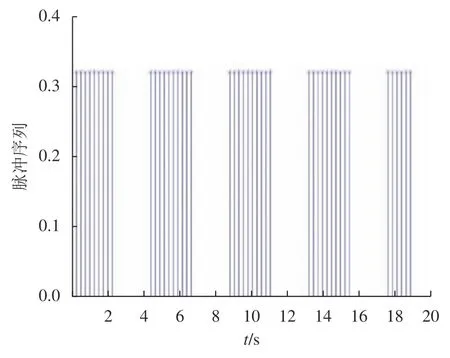
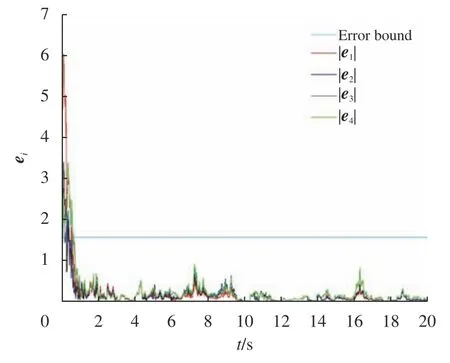
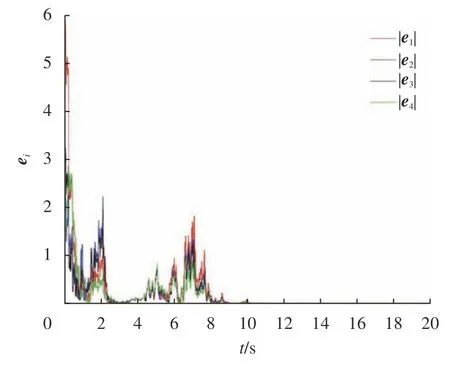
式中:ηk,dk和 ψk分别表示脉冲增益、替代攻击的强度和虚假数据注入攻击的强度,且 ηk与ψk需要满足条件一定的条件,详见备注3。δ(·)表示狄拉克函数。{tk,k∈N+}表示脉冲序列,其中,N+是正整数集,该序列满足0=t0 此外,假设由式(1)和(3)所组成的领导跟随随机多智能体系统状态初值为,其中t0≥0为初始时刻。 备注1如图1所示,两种不同欺骗攻击发生在传感器到控制器或控制器到执行器的信道上,且是相互独立的。当替代攻击成功发生时,控制信号将会被篡改为欺骗攻击信号;当虚假数据注入攻击成功发生时,虚假数据则会附加到控制信号中。 图1 两种不同欺骗攻击的攻击原理图Fig.1 Configuration of two different deception attacks 将控制协议(4)代入系统(1)中,可得到遭受两种欺骗攻击下跟随者的状态方程如下。 为实现式(1)与式(3)所组成的领导跟随随机多智能体系统在两种欺骗攻击情况下的均方拟一致性,构建如下误差系统。 式中:ei(t)=xi(t)−x0(t),=f(t,xi(t))−f(t,x0(t)),。 备注2两种欺骗攻击是相互独立的,也就是说它们的攻击时刻可以是不一样的,但均属于脉冲序列{tk,k∈N+}。不同欺骗攻击具体出现的攻击时刻由{tk,k∈N+}、αi(tk)与βi(tk)共同决定。 式中:G(tk)=diag{α1(tk),α2(tk),···,αN(tk)}∈RN×N,Λ(tk)=diag{β1(tk),β2(tk),···,βN(tk)}∈RN×N及。 备注3当αi(tk)=0,βi(tk)=1时,即控制信号仅受到虚假数据注入攻击时,ηk与ψk需要满足条件|λmax(IN+ηkH−ηkG(tk)H+ψkΛ(tk))|≥1,其中,λmax(·),λmin(·)分别表示对称矩阵特征值的最大值和最小值。这是因为如果µ=|λmax(IN+ηkH−ηkG(tk)H+ψkΛ(tk))|≤1,有e(tk)≤,则此时攻击依然起到脉冲控制作用,与攻击的定义相违背。 以下是本文用到的引理、假设及定义。 引理1令向量ζ,Υ∈Rn,ε>0,则有 ζTΥ+ΥTζ≤εζTζ+ε−1ΥTΥ. 假设1非线性函数f:R×Rn→Rn和:R×Rn→Rn×m满足如下的李普希兹条件 假设2替代攻击信号ξ(tk),k∈N+有界且满足如下条件: ∥ξ(tk)∥2≤ξ 式中:ξ<+∞是一个已知非负实数。 定义1对于任意给定的系统初值ϕ(t0),如果存在一个闭集和常数≥0使e(t)满足条件 则称由式(1)和式(3)组成的领导跟随随机多智能体系统实现均方拟一致性,且具有均方误差极限的上界;若=0,则称系统可实现均方一致性。 定义2对函数V:R×Rn→R+,定义运算符L : 式中:tr[·]表示矩阵的迹。此外,Vt(t,y),Vyy(t,y)与Vy(t,y)分别定义为 定理1在假设1~2成立的情况下,若存在ε>0满足以下条件 证明考虑以下李雅普诺夫函数 由伊藤公式可知,当t∈[tk−1,tk),k∈N+,有 由假设1可得 当t∈[tk−1,tk),k∈N+,令ι>0 足够小且满足t+ι∈[tk−1,tk),有 由此可知,有D+E[V(t,e(t))]=E[LV(t,e(t))]。 当t∈[tk−1,tk),k∈N+,结合式(14)与(15),有 当t=tk,k∈N+时,由误差系统(8)可知 根据式(11)与式(18)可知 式中W(tk)=dkG(tk)⊗In,M(tk)=(IN+ηkH−ηkG(tk)H+ψkΛ(tk))⊗In。 对于式(19)中的第一项,有 对式(19)中的第二项和第三项,结合引理1, 对式(19)中的最后一项,有 将式(20)~(22)代入式(19)中,有 对t∈[t0,t1),由式(17)可知, 由此可知,当t=t1时,有 对t∈[t1,t2),同理有 由此可知,当t=t2时,有 通过迭代法,当t∈[tk,tk+1),有 因此,当t→∞时,由(25)可得 为验证本文结果的有效性,本节考虑由5个3维智能体所组成的蔡氏循环电路组合,其中包含1个领导者和4个跟随者。系统通信拓扑如图2所示。 图2 循环电路组回路拓扑图Fig.2 Topological diagram of each sub loop in the cycle circuit combination 设跟随者动力学方程(1)和领导者动力学方程(3)中状态为xi(t)=[xi1(t),xi2(t),xi3(t)]T,i∈N∪{0},其他参数的选择为 非线性函数选择f(t,xi(t))=[0.4sat(xi1(t)),0,0]T,=0.4|sat(xi(t))|I3,sat(xi(t))=0.5(|xi(t)+1|−|xi(t)−1|),sat(·)为饱和函数,i=1,2,3。同时,由假设1可以得到=0.4 与Φ=diag{0.4,0.4,0.4}。此外,选择=0.5。 考虑式(4)所设计的控制协议,其中控制增益选择为η≡−0.32,攻击强度为d≡0.2。替代攻击的攻击信号ξi=(0.1,0.14,−0.14)T,同时由假设2可得ξ=0.049 2。同理,设虚假数据注入攻击的攻击信号xi=(0.1,0.15,−0.15)T,攻击强度ψ≡0.43。同时,选择=0.2与=0.5。 系统(1)采用的脉冲序列如图3所示,设最大控制脉冲间隔τsup==2,令仿真步长为0.1,结合给定的初始条件与本节所选择和计算得到的参数在MATLAB中仿真得到图4。由图4可知,由式(1)与式(3)所组成的领导跟随随机多智能体系统受到两种不同脉冲欺骗攻击时,在控制协议(4)作用下可实现均方拟一致性,即误差保持在所计算的误差界限内。若不发生脉冲欺骗攻击时,可得到系统的均方一致性,如图5所示。 图3 系统(1)脉冲控制信号Fig.3 The impulse control signal of system (1) 图4 受到两种欺骗攻击时系统的误差轨迹图Fig.4 The errors' trajectories of the system with two different deception attacks 图5 无欺骗攻击时系统的误差轨迹图Fig.5 The errors' trajectories of the system without deception attacks 假设系统初始时刻为t0=0,其初始状态值随机选择为 此外,令ε=1。根据上述所选择的参数,可计算得到误差上界为=1.566。据此可知,上述参数可满足定理1中的条件,故由式(1)与式(3)所组成的领导跟随随机多智能体系统在两种不同的欺骗攻击作用下可实现均方拟一致性,且其收敛率为−ρ=1.8。 基于脉冲控制方法,本文研究了一类领导跟随随机多智能体系统在遭受替代攻击和虚假数据注入攻击下的均方拟一致性问题。不同于已有文献,本文同时考虑了两种不同脉冲欺骗攻击对系统均方拟一致性的影响,其中攻击模型采用两个服从伯努利分布的随机变量来描述不同攻击的成功与否,更适用于模拟现实应用中的情形。基于李雅普诺夫稳定性理论和相关随机过程知识,本文给出了两种不同脉冲欺骗攻击下系统实现均方拟一致性的充分条件,同时也给出了误差极限的上界。最后,通过数值仿真例子验证了研究结果的有效性。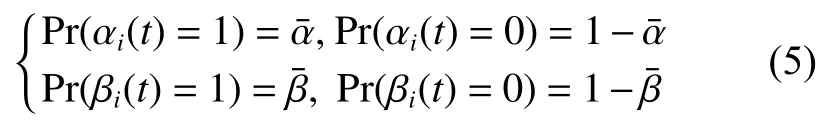

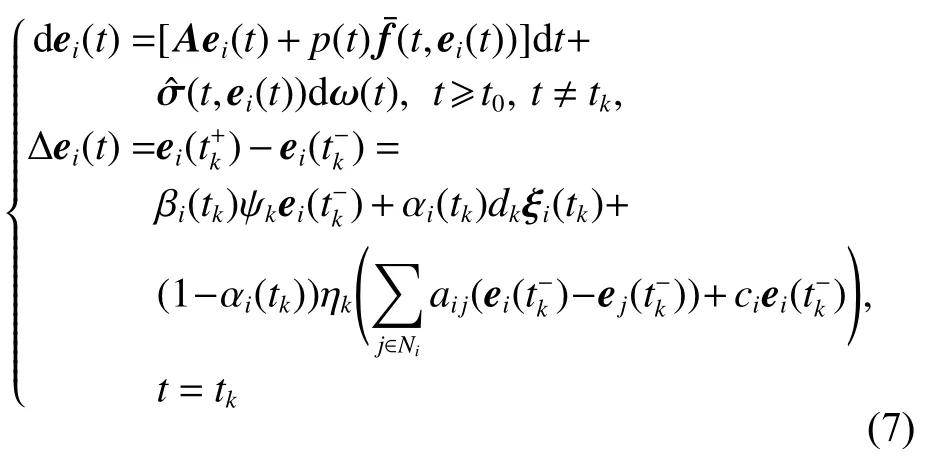
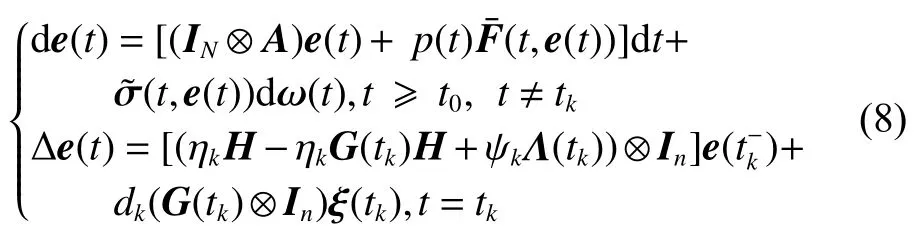

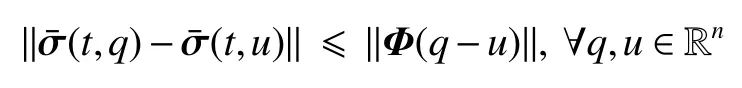
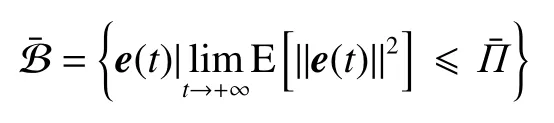
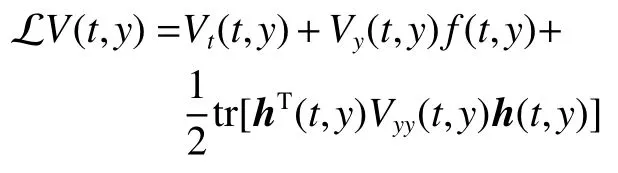
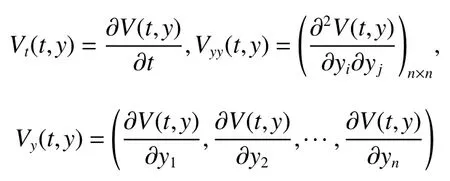
2 一致性分析
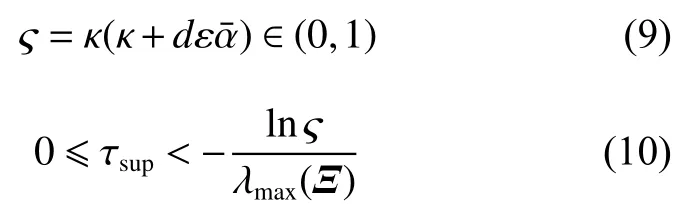


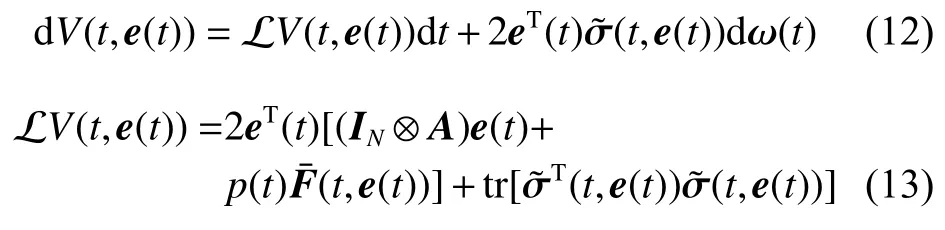
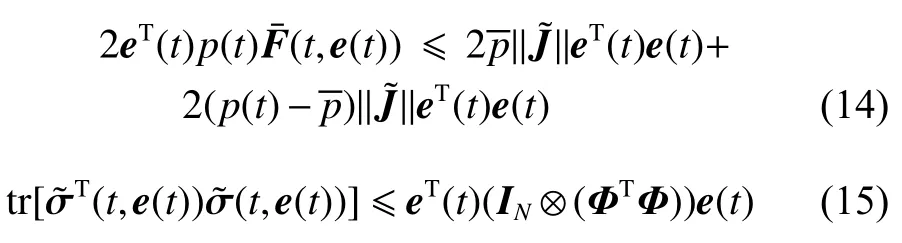
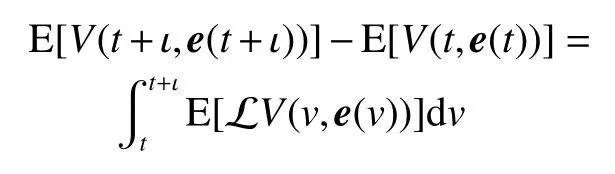

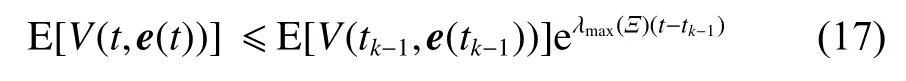
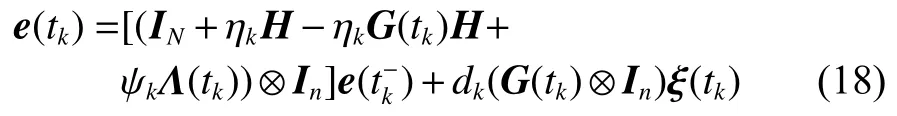
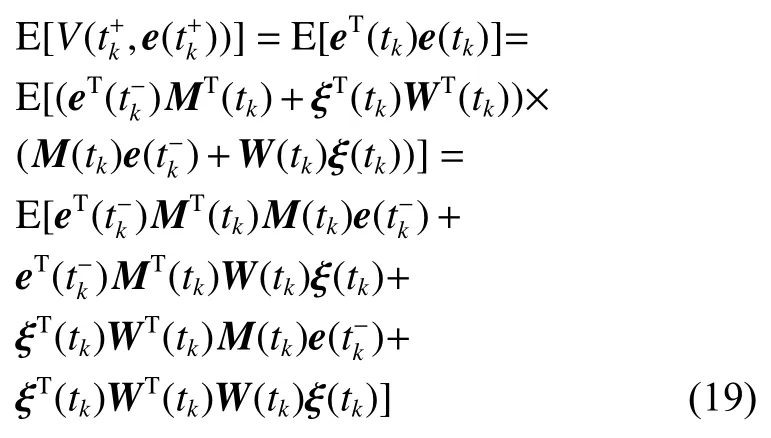
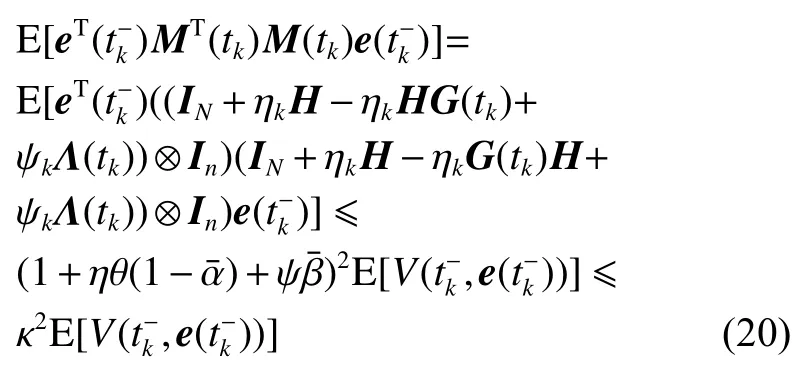
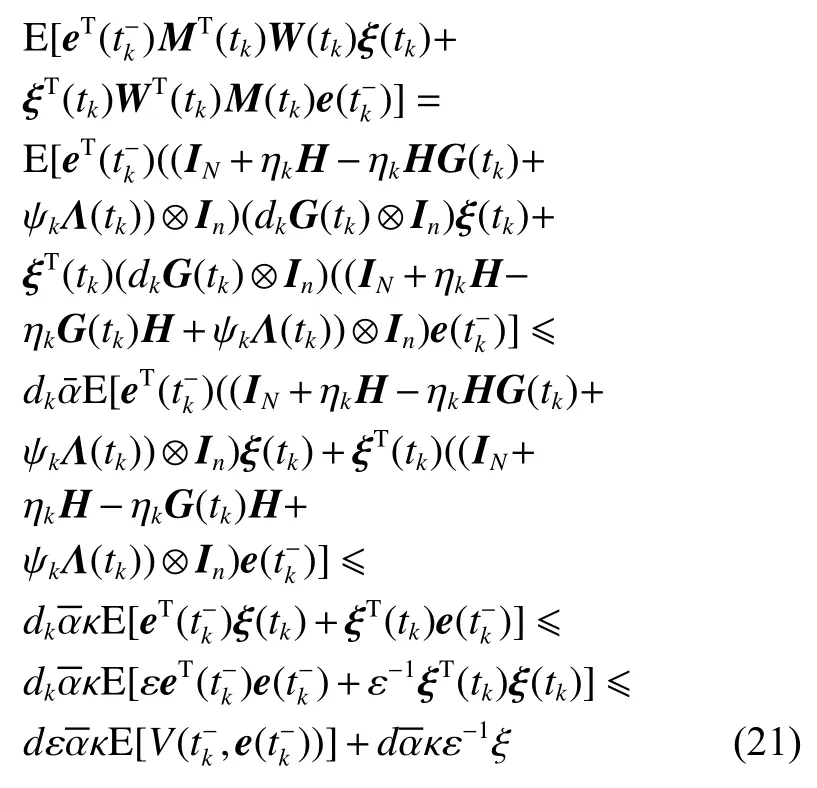
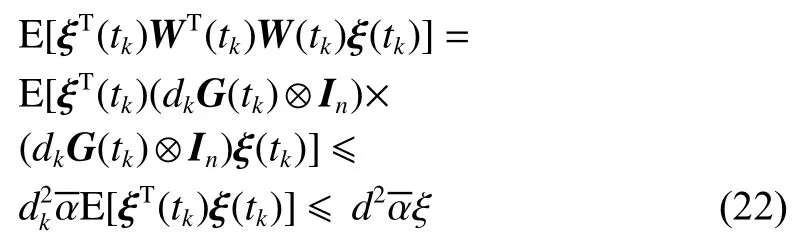
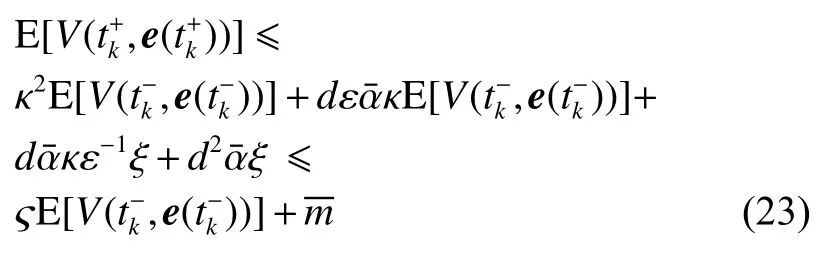
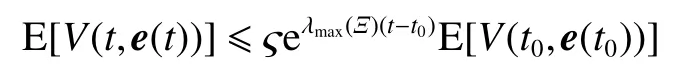
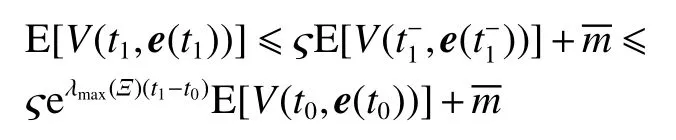
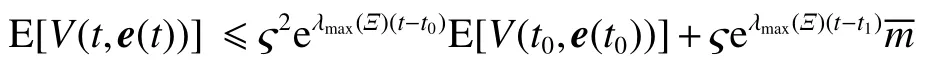
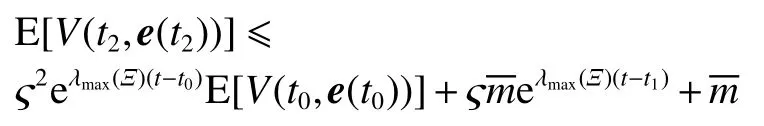
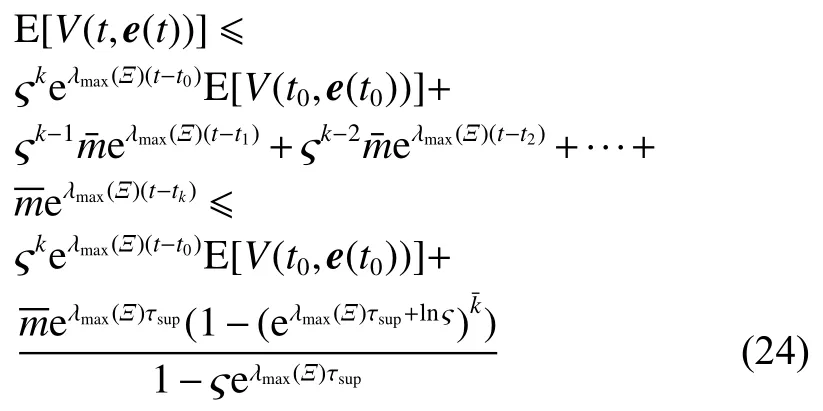
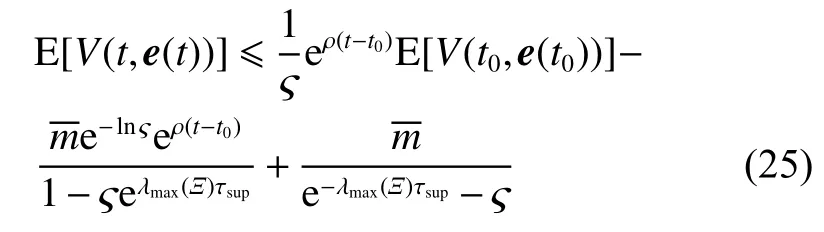
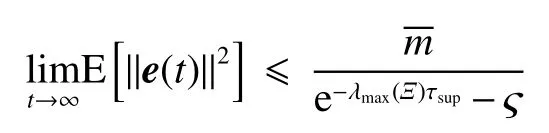
3 数字仿真
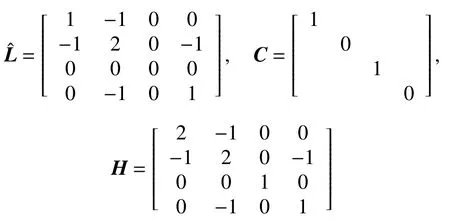

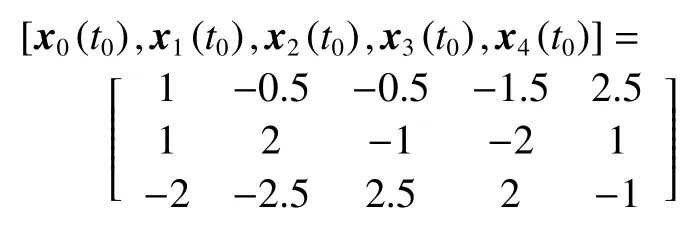
4 结论

