柔性多指灵巧手工作空间研究*
李雨健 , 张新星
(衢州职业技术学院机电工程学院,浙江 衢州 324000)
0 引言
随着我国饮食结构的变化,脑血管病多发,尤其脑卒中患者数量在急剧增加。脑卒中发病率高,死亡率高,还具有高致残性,从而导致人体各类运动功能障碍[1]。其中,手部运动功能障碍的患者往往生活不便,给家庭带来了严重的负担[2]。为了使患者方便进行物理康复治疗,各种各样的手部康复器被研制出来。机器人柔性多指灵巧手可以辅助患者进行手部的弯曲、伸展等运动,还能辅助完成日常生活中的抓取动作。机器人柔性多指灵巧手因具有柔顺性、多功能性等特点,备受社会各界期待[3]。与此同时,对手部康复柔性多指灵巧手的应用也提出了更多期待,如优化结构设计等。灵巧手在抓取时,可能会因指尖末端达不到抓取区域而造成抓取任务失败,所以需要研究灵巧手的工作空间区域,从而改进结构设计,使其工作空间更加贴合实际。因此,研制一款可靠、安全、易用、工作空间合适的手部康复柔性多指灵巧手,帮助广大脑卒中患者恢复手部运动功能,是十分必要的。柔性多指灵巧手如图1所示。

图1 灵巧手
1 运动模型建立
柔性多指灵巧手的运动,往往由电机带动。即对于电机而言,给定相应的脉冲,各个电机就转动,从而带动灵巧手机构转动相应的角度。在实际操作中,重要的是柔性多指灵巧手末端的手指所能到达的位置和姿态,因此需要建立手指指尖位姿和各关节角度的关系,这就是运动学模型[4]。柔性多指灵巧手运动学问题可分为正向、逆向运动学。正向运动学即已知各关节的角度,来求解指尖在笛卡尔坐标系下的位姿;逆向运动学即已知指尖在空间下的位姿,反求各关节角度。
经过几十万年的进化和自然界的优胜劣汰,人类的手部基本已经达到了最优结构,能够抓取任意形状的物体,完成各种复杂精细的操作。人手解剖图如图2所示。多指灵巧手以人手为原型,由5个运动相互独立的单指机构构成。由图2可知,每根手指都由远、中、近3个指节和腕掌关节组成。近节指骨、远节指骨和中节指骨都能实现弯曲动作,但远节指骨不能独立弯曲,只能随同中节指骨一起运动。考虑到腕掌处的回转,在单个手指的根部在增加一个回转机构。从机构学的角度分析,一个弯曲运动等同于转动,故单个手指具有3个转动和1个回转自由度。
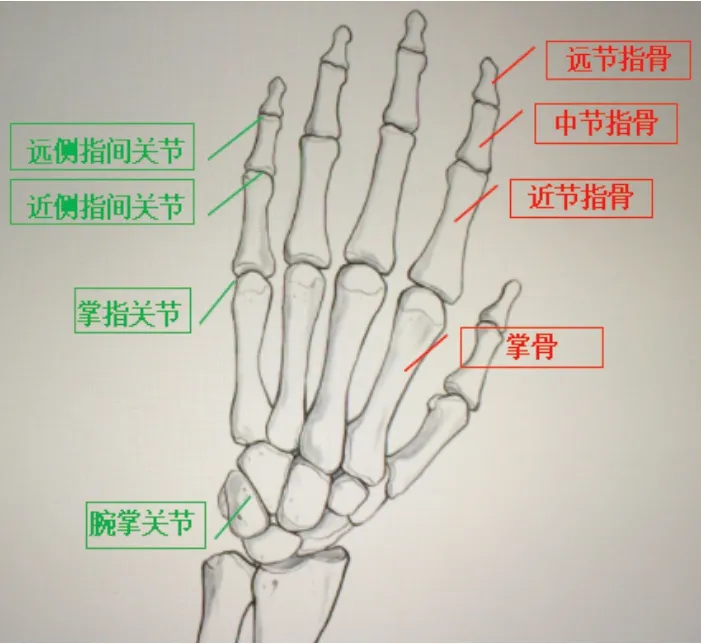
图2 人手解剖图
单指机构类同串联机械臂,其可以简化为由若干个刚体连杆组成,连杆由关节(运动副)连接起来,每个关节有转动的自由度。每个关节的运动状态决定了其下一关节连杆在空间坐标系中的姿态和位置。美国科学家Denavit和Hartenberg基于此提出了简单实用的D-H参数法,其包含连杆长度a,扭角α,偏距d,关节角θ这4个参数,用于将参考坐标系附加到空间运动链或机器人操作臂的连杆上[5]。对真实的柔性多指灵巧手进行运动机构简化,在其连杆上建立坐标系,如图3所示。
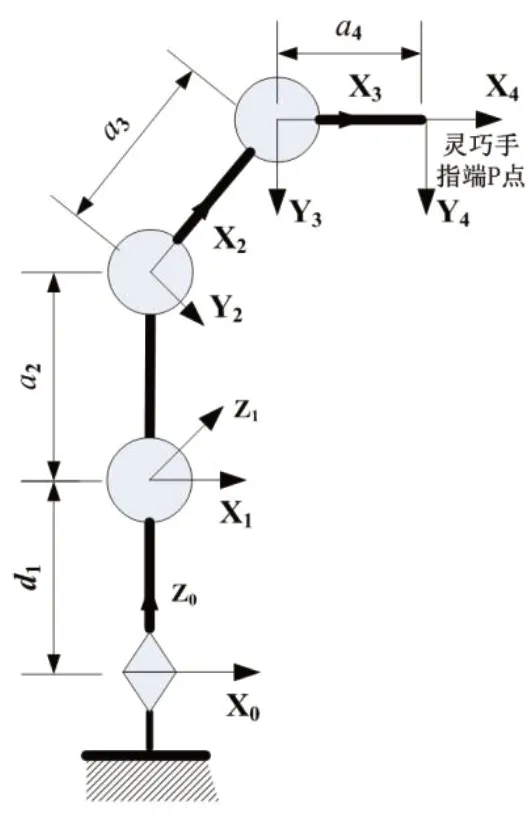
图3 运动结构简图和坐标系
依据所建立的坐标系得出的D-H参数表,如表1所示。
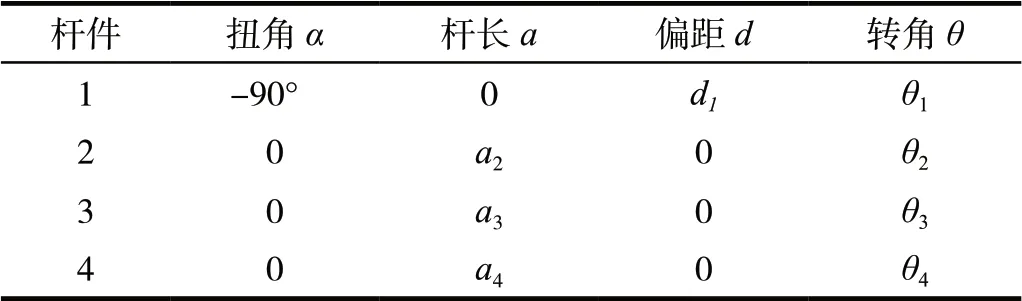
表1 D-H参数表
在运动学中,各坐标系之间的平移和转动可以用齐次坐标变换来表示。即在灵巧手笛卡尔空间中,灵巧手末端的位姿变化可以用齐次变换矩阵来描述。根据上述的各连杆坐标系和D-H参数法,可以用如下的齐次变换矩阵来说明依附在相邻两个关节间上的坐标系的转动[6]。
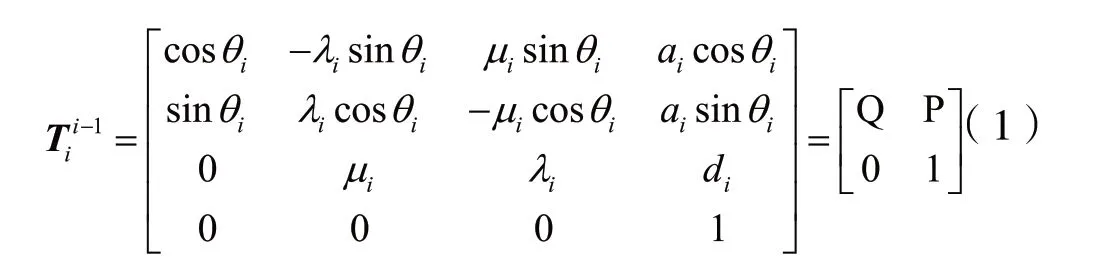
根据表1的D-H参数表,将相应数据代入,得:
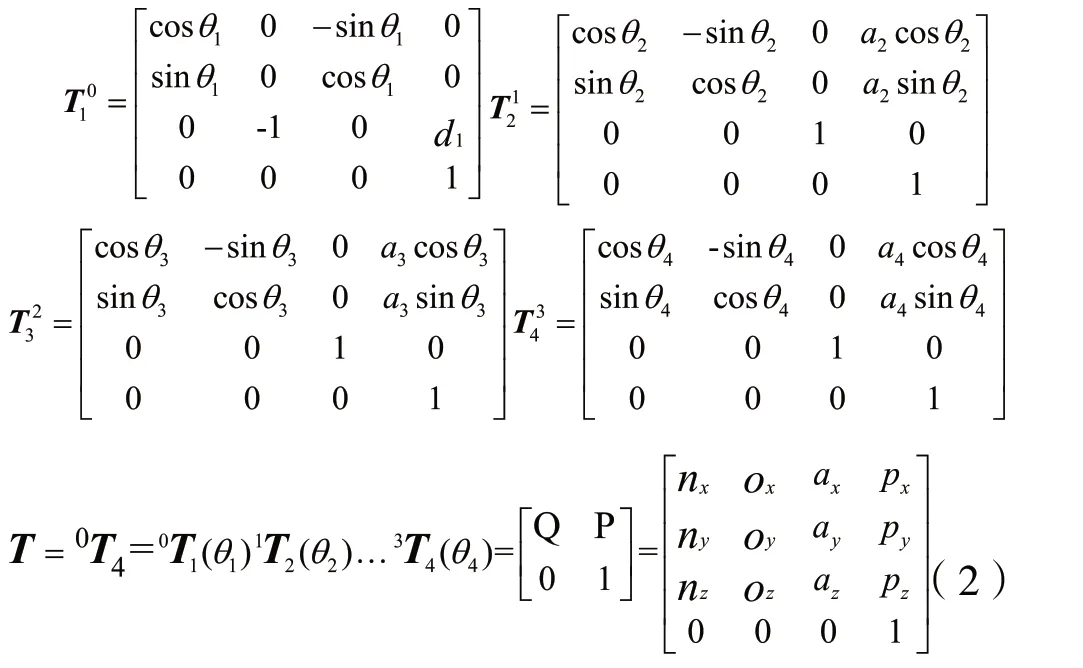
上述表达式中矩阵P的具体坐标如下:
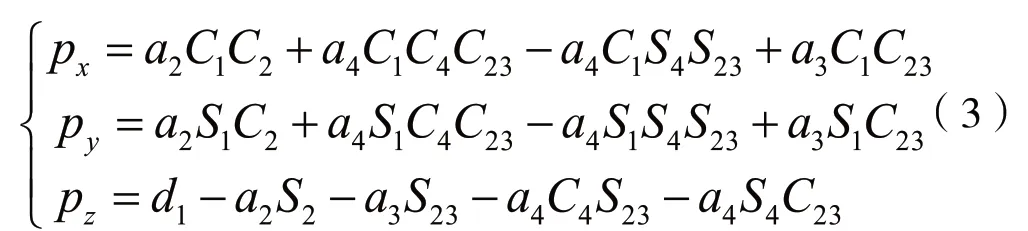
灵巧手各指的机构参数基本一致,因此各手指的运动学方程相对各自的定参考坐标系是相类似的,对单指机构的位姿方程正向求解的分析研究方法同理可以引申到其余多指。
2 工作空间分析
单指的主要运动形式是腕掌处的回转和手指3个关节的转动。灵巧手手指各个关节在对应的角度范围内转动,手指指尖在笛卡尔空间下随之运动,其在空间中各个位置的坐标点的集合,即为该手指的工作空间[7-8]。求解串联的灵巧手工作空间的方法主要有数值法、图解法、解析法[9-10]。由于解析法难以应用到多自由度机械手、图解法不够准确等原因,数值法在求解工作空间时应用比较多。数值法中,比较普遍的方法是蒙特卡洛法,主要步骤是根据运动学模型分析得出的手指指尖在空间的位置坐标给定各结构参数,赋值θ1~θ4并遍历关节角范围内所有取值,得出各坐标点,从而构造出边界轮廓,得出工作空间。
根据仿生学相关资料[11],以中指为例,近节指骨、中节指骨和远节指骨的长度基本为44.5 mm、28 mm、16.5 mm,掌骨长度为50 mm,近、中节指骨的弯曲范围为0~90°,远节指骨弯曲范围为0~60°,关节1的回转角度为±50°。因此,单个手指的结构变量参数如表2所示。

表2 手指的结构变量参数表
依据上述步骤,在MATLAB中利用For-End函数遍历搜寻各个符合要求的关节角度,再利用Scatter函数打点,完成灵巧手工作空间的仿真分析[12]。固定θ1=0,遍历取值θ2~θ4,即可得出灵巧手的X-Z二维工作空间,如图4所示,其在X、Z方向上的最大运动范围大约为-50 mm~100 mm、-40 mm~50 mm。固定θ1=90°,遍历取值θ2~θ4,即可得出灵巧手的Y-Z二维工作空间,如图5所示,其在Y、Z方向上的最大运动范围大约为-40 mm~80 mm、-40 mm~50 mm。遍历取值θ1~θ4,即可得出灵巧手的三维工作空间,如图6所示。
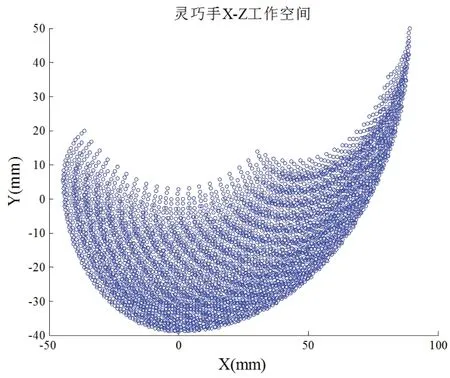
图4 灵巧手XOZ二维工作空间
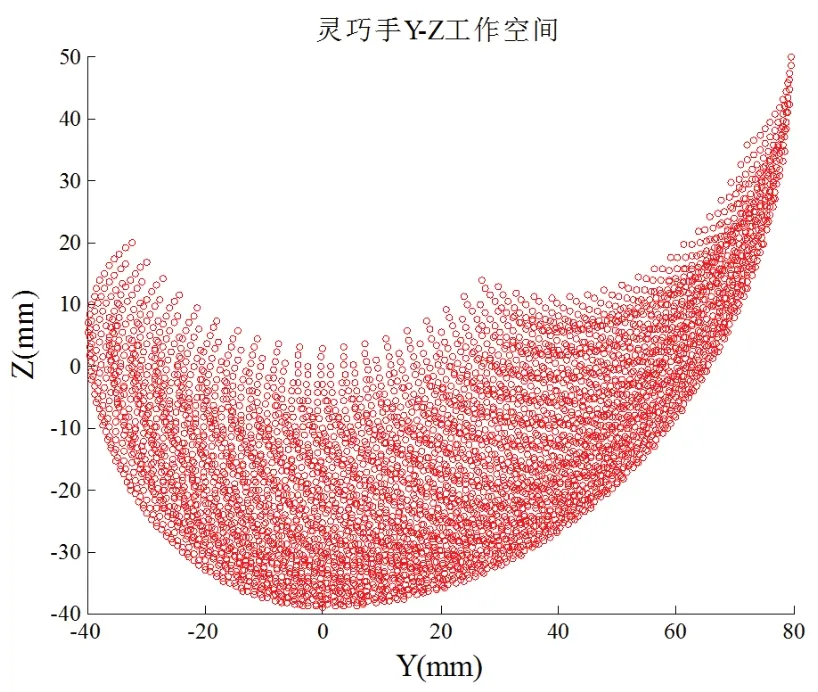
图5 灵巧手YOZ二维工作空间
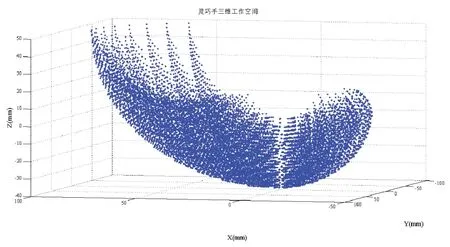
图6 灵巧手三维工作空间
3 结论
依据D-H参数,推导灵巧手的正运动学模型,从而得到了灵巧手在空间中的位置坐标,最后结合蒙特卡洛法使用MATLAB进行仿真分析,得出了柔性多指灵巧手的单指二维、三维工作空间。该工作空间点位分布均匀且直观性强,为后续的结构设计优化提供理论支撑。

