基于差分进化鲸鱼优化算法的森林冠层图像分割

邬博文，朱良宽，王璟瑀

(东北林业大学 机电工程学院，黑龙江 哈尔滨 150040)

在森林生态系统研究中，冠层参数占据着重要地位[1]。这些参数控制着光合作用、空气污染物沉积等生态过程，为森林生态系统各项生态指标的观测提供了直观依据。在冠层参数的获取方法中，基于图像分割的方法受到广泛研究，其基本原理是通过图像分割的方法获取冠层孔隙度，即天空面积占图像总面积的比率，进而通过公示反演各种森林冠层参数[2]。

图像分割是图像处理与分析领域中的一个经典问题，也是该领域的难点之一[3]。通过将像素点划分到不同的类别区域，完成对图像中目标的分类提取过程。图像分割的主要方法有基于阈值[4]、边缘[5]、区域[6]、聚类[7]和人工神经网络[8]的方法等。其中，阈值分割具有效果明显、易于实现、实时性良好的特点[9]，被认为是目前最流行的图像分割技术之一[10]。在阈值分割方法中，基于直方图区域划分的阈值选取准则是近年来的研究热点[11]，常用的方法有Otsu法、Kapur熵法等[4,12]。其中，Otsu法更加侧重于类内像素灰度级的均匀性，使目标类和背景类所占的区域面积趋于相等，适用于图像中目标类和背景类面积相差不大的情况，而Kapur熵法依据灰度级类内概率，所划分的目标和背景的大小并不十分敏感，能够较好地保留图像中的小目标[11]。

基于阈值方法的图像分割，实质上是在复杂参数空间里寻求最优分割阈值的问题[13]。为了处理具有多个目标的复杂图像，研究者们将算法从单阈值扩展到多阈值[14]。然而，随着阈值个数的增多，问题的计算复杂程度呈指数式上升[15]。为了解决该问题，许多研究者将智能优化算法应用于这一领域。B.Khorrametal[10]提出了一种基于改进蚁群算法的阈值分割方法应用于磁共振脑图像分割，通过引入不同方向概率的纹理特征，提高算法的搜索能力。邢致恺等[16]提出了一种基于改进樽海鞘群优化算法的阈值分割方法并应用于污油图像，通过引入Levy飞行策略增强算法的全局搜索与收敛能力，从而获得更为准确的分割阈值和更高的分割效率。除此之外，还有许多的智能优化算法被应用于阈值分割领域，如粒子群算法(PSO)[17]、人工蜂群算法(ABC)[18]、风驱动算法(WDO)[19]等。上述将智能优化算法引入图像分割的研究，都取得了一定的成果。但大多数优化算法的整体机制仍然是先侧重全局探索，后进行局部开发。这种机制的收敛速度较慢，在迭代后期缺乏跳出局部最优的能力。此外，上述研究中的智能优化算法，大多需要根据应用场景和对象的不同而调整许多参数，影响了算法的工程实用性。

在运用图像分割技术进行森林冠层研究时，自然环境下采集到的冠层图像容易受到光照和自身复杂结构的影响，导致过亮区域天空与冠层树梢、树干反光部分边界模糊，阴影区域冠层结构色彩区分不明显，造成了冠层图像的分割困难。针对此问题，多阈值分割将不同灰度级的目标划分到不同区域，能够有效解决单阈值分割处理困难的复杂多目标图像。但多阈值分割的计算复杂程度受阈值数影响较大，阈值数过大时算法的实时性较差。上述这些实际问题促使一种有效技术的引入。

WOA算法是一种参数设置简单但功能全面的算法，其拥有开发和勘探2种机制，同时能在小概率下进行随机搜索。这种均衡的机制使得WOA算法在进行全局搜索的同时还拥有跳出局部最优的能力。另外，WOA算法的参数设置少，处理不同的优化问题时不需要额外调整参数，使其具有较好的工程实用性。C.Langetal[20]提出了一种混合鲸鱼优化算法并应用于彩色图像分割，通过引入DE算法作为局部搜索策略，有效提高算法的局部开发能力，同时在迭代后期保持种群多样性。M.M.Mafarjaetal[21]设计了WOA算法和模拟退火算法(SA)2种不同的混合模型，并将其应用于特征选择领域，利用SA算法优化WOA算法每次迭代后的最优解，提高了算法的分类准确性。Z.Yanetal[22]提出了一种基于Levy飞行策略和变异算子的改进鲸鱼优化算法并应用于解决工程设计问题，改进算法扩大了搜索空间，避免了早熟收敛，同时增加了个体最优选择的概率，增强了寻优能力。

综上所述，这些研究成功的案例证明了WOA算法的优越性，本研究拟将混合WOA算法引入森林冠层图像分割领域，提出基于DE-WOA优化算法的多阈值Kapur熵森林冠层图像分割方法。将DEA算法作为局部搜索策略嵌入WOA算法，并引入一种以种群适应度为评价指标的算法混合策略来平衡2种算法。将DE-WOA算法应用在森林冠层图像分割试验中，利用图像质量评价指标进行分析，比较DE-WOA算法与PSO、WOA 2种算法的效果，验证混合算法分割精度高的特点。

1 材料与方法

1.1 数据源及试验环境

所用的森林冠层图像来源于东北林业大学凉水实验林场(凉水国家级自然保护区)，凉水实验林场是东北林业大学直属的教学实践基地，位于黑龙江省伊春市(128°47′8″-128°57′19″E，47°6′49″-47°16′10″N)，东西宽13.0 km，南北长17.0 km，总面积为12 133万m2，其林木种类包括白桦(Betulaplatyphylla)次生林、阔叶红松(Pinuskoraiensis)林等。冠层图像由带有鱼眼镜头的图像采集设备获得，分辨率为2 736×2 736。试验在2.20 GHz CPU和12GB内存的PC机、windows7操作系统和Matlab R2016b环境中进行。

1.2 问题分析

首先对冠层图像存在的光照情况进行分析，以便于验证所提算法在森林冠层图像上的适用性。选取2幅光照不均的森林冠层图像(冠层1、2)作为本研究实验对象，与拍摄条件较理想的森林冠层图像(冠层3)进行直方图比对(图1)。森林冠层图像在阳光作用下易产生光照不均匀现象，具体表现为冠层1、冠层2在暗色区域色彩分布较为集中，位置较极端，变化陡峭且缺少部分低级灰度，导致其相对冠层3存在褪色现象；同时冠层图像在树梢等部分均存在一定程度的反光干扰，灰度分布接近上限，导致天空与冠层边界模糊。由于林木冠层的复杂性，拍摄冠层图像时很难避免这些影响，这对分割方法提出了更高的要求。

1.3 研究方法

1.3.1 差分进化鲸鱼优化算法

1.3.1.1 鲸鱼优化算法 WOA算法是2016年由澳大利亚学者S.Mirialilietal[23]提出的一种新型群体智能优化算法，该算法模拟鲸鱼的泡泡网捕食行为，设计收缩包围机制和螺旋更新位置机制，模拟鲸鱼种群包围、追捕、攻击猎物等过程实现优化搜索。

在该算法中，猎物的位置对应于问题的全局最优解，鲸鱼能够识别猎物的位置并包围它们，假设鲸鱼种群规模为N，搜索空间为d维，第i只鲸鱼在d维空间中的位置Xi表示为。

(1)

收缩包围机制：由于在求解优化问题前对搜索空间的全局最优解没有先验知识，假设当前群体中的最优位置为猎物，群体中其他鲸鱼个体均向最优个体包围，具体表现如下[24]。

D=|C·X*(t)-X(t)|

(2)

X(t+1)=X*(t)-A·D

(3)

式中：t为当前迭代次数；X*(t)为群体最优解位置；X(t)为个体位置；A和C为系数向量，A=2a·r1-a，C=2·r2，r1和r2为[0,1]范围内的随机数；a是从2线性减小到0的常数。

螺旋更新机制：模拟鲸鱼捕获猎物时的螺旋式运动，其数学模型如下。

D′=|X*(t)-X(t)|

(4)

X(t+1)=D′·ebl·cos(2πl)+X*(t)

(5)

式中：D′表示个体与群体最优解之间的距离；b是常数；l为[-1,1]间的随机数。

在猎食过程当中，鲸鱼绕猎物做缩紧环状游动，同时沿螺旋路径行进。为了模拟这2种机制的同时执行，设置更新机制概率p均为0.5，其数学模型如下。

(6)

随机猎食机制：除上述泡泡网捕食行为外，鲸鱼还可以根据种群中随机个体的位置搜索猎物，而不是当前最优解。这种机制增强了算法的全局搜索能力，其数学模型如下。

D=|C·Xrand-X(t)|

(7)

X(t+1)=Xrand-A·D

(8)

式中：Xrand为随机选取的个体位置。

1.3.1.2 鲸鱼优化算法的改进 WOA算法作为一种新型群智能优化算法，虽然具有较强的全局搜索能力，但仍存在一些不足，如在易陷入局部最优、探索和开发不平衡等问题。而差分进化算法是一种计算过程简单但功能强大的算法，其仿生机制可以缩小种群间个体差异，迫使搜索个体离开当前区域，从而避免陷于局部最优。通过合适的算法混合策略，将差分进化算法作为一个部分嵌入WOA算法，能够增强局部开发能力，提升解的精度。

1)差分进化算法(DEA)

变异操作：变异操作是差分进化算法与其余进化算法的主要区别，用于产生变异个体Vi,G+1，数学表示为：

Vi,G+1=Xr1,G+SF·(Xr2,G-Xr3,G)

(9)

式中：Xr1,G，Xr2,G，Xr3,G是种群中3个不相同的G代个体；变异因子SF为[0,1]之间的随机数。

交叉操作：交叉操作将变异个体Vi,G+1与目标个体Xi,G进行杂交，经过杂交后得到目标个体的候选个体Ui,G+1，数学表示为：

(10)

式中：交叉因子CR为[0,1]间随机数。

选择操作：选择操作将候选个体Ui,G+1与目标个体Xi,G进行适应度比较，进而判断是否在下一代中选择用候选个体替换目标个体，对于目标函数为最小化的问题，其数学表示为：

(11)

式中：f为求解问题的适应度函数。

2)算法混合策略

为了平衡DE-WOA算法的探索与开发，引入一种以种群平均适应度为个体评价指标的算法混合策略。种群的平均适应度反映了种群个体的整体质量。对于一个最小化问题，如果新个体的的适应度小于种群平均适应度，则表明该个体所处的位置是具有开发前景的，应采用局部开发策略以保证收敛速度；如果新个体的的适应度大于种群平均适应度，则表明该个体所处的位置质量较差，可以采用全局搜索策略探索未知区域，避免局部最优。

1.3.2 差分进化鲸鱼优化算法应用于图像阈值分割 图像分割的阈值选取可以视作一个优化问题，将阈值选取的准则函数作为优化算法的适应度函数，则算法中个体的位置对应于准则函数的解，即选取的阈值，通过对优化问题选取最优解来选取最佳阈值[11]。

对于单阈值分割,用所寻得的最优阈值t将图像灰度f(x,y)分为前景和背景两类，数学表达式如下：

(12)

对于多阈值分割，假设n个阈值为[t1,t2,…,tn]，则灰度级映射为：

(13)

式中：l0,l1,…,ln为分割后图像的n+1个灰度级，L=256。

Kapur熵是一种基于信息熵的自动阈值选取技术。其阈值选取准则是使分割后的目标类和背景类的总熵值最大，即总信息量最大。由于其对前景背景面积的不敏感，擅长保留图像中的小目标，因此被广泛应用于复杂图像分割问题。

假设图像选取的n个阈值，那么Kapur熵的目标函数可以定义为：

H(t1,t2,…,tn)=H0+H1+…+Hn

(14)

其中

(15)

式中：Hn表示分割后不同类的熵；ωn表示每一类像素点的概率；Pj表示灰度值为j的像素点出现的概率。

为了选取最优阈值组合，利用下式进行判断：

fkapur=arg max{H(t1,t2,…,tn)}

(16)

使Kapur熵函数值fkapur最大化的熵值即为所求的最优阈值，针对传统穷举方法效率低下的问题，引入智能优化算法对阈值组合的选取过程进行优化改进，提升阈值选取的计算速度与精度，算法流程见图2。

2 结果与分析

2.1 单阈值分割试验

利用单阈值Kapur熵法对森林冠层图像进行分割，试验结果见图3。

可以看出，单阈值Kapur熵分割法能够有效地分割冠层与天空区域。但对于局部反光的树梢、树干区域和冠层复杂区域，该方法存在较多的欠分割现象，即将反光区域错分为天空。为了解决该问题，选用多阈值Kapur熵方法对森林冠层图像进行分割。

2.2 多阈值分割试验

对试验对象分别进行阈值个数为2、4、6的图像分割，并应用所提算法与WOA算法、PSO优化算法对阈值选取过程进行优化，进行试验和对比分析。优化算法的参数设置见表1。

表1 算法参数设置Table 1 Algorithm parameter setting

表2给出了3种算法应用于森林图像分割时的最佳分割阈值和Kapur熵值。可以看出，对于森林冠层图像的分割，在分割阈值个数较小时，DE-WOA方法与其余2种方法的分割精度相差不大，随着阈值求解问题维度的上升，DE-WOA所优化的分割算法展现出更好的性能。

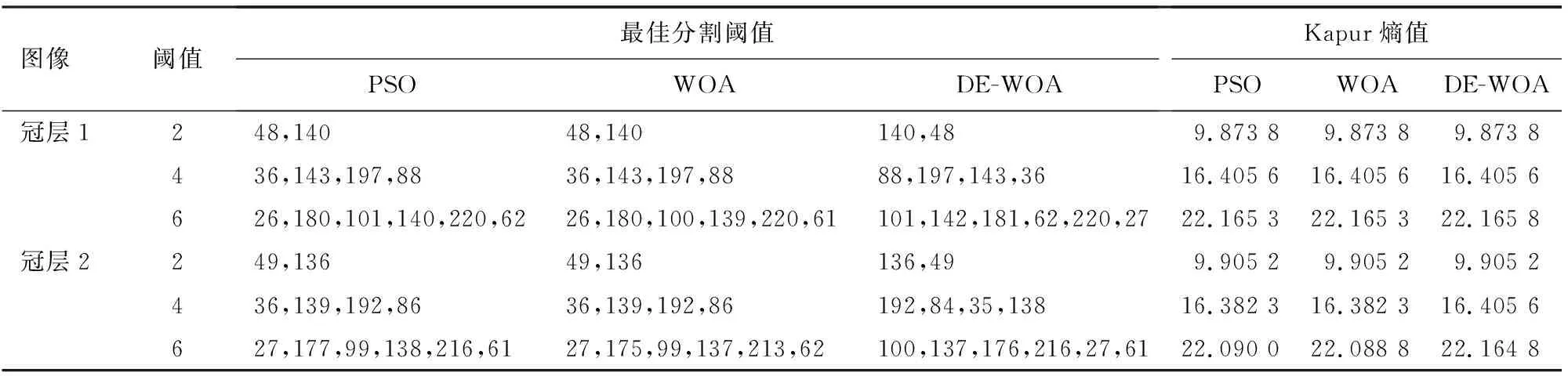
表2 3种算法得出的图像分割阈值与Kapur熵值Table 2 Image segmentation threshold and Kapur entropy obtained by three algorithms

为了客观地体现DE-WOA算法在森林冠层图像分割效果的优越性，采用图像的峰值信噪比PSNR、结构相似性SSIM来对算法的性能进行评判，2个指标数学表示如下。

2.1.1 PSNR(公式中用PSNR表示)

(17)

(18)

式中：I(i,j)、I′(i,j)分别为原图像和分割图像；H、W为图像尺寸；RMSE为RMSE的值。

2.1.2 SSIM(公式中用SSIM表示)

SSIM(I,I′)=l(I,I′)×c(I,I′)×s(I,I′)

(19)

(20)

(21)

(22)

式中：μI、μI′表示原图像与分割图像的均值；σX、σY表示原图像与分割图像的方差；σXY表示原图像与分割图像的协方差；C1、C2、C3为常数,C1=(0.01×L)2,C2=(0.03×L2,C3=C2/2,L=255。

表3给出了对于2幅森林冠层图像进行分割试验后计算的PSNR、SSIM值。可以看出，在阈值个数为2时，DE-WOA算法的PSNR值较PSO、WOA算法提升0.009 8 dB，而SSIM值与其他2种持平；在阈值个数为4时，DE-WOA算法的PSNR值较PSO、WOA算法提升0.163 dB，SSIM值提升0.129；在阈值个数为6时，DE-WOA算法的PSNR值较PSO、WOA算法分别提升0.230、0.235 dB，SSIM值提升0.539、0.536；可DE-WOA算法随着计算复杂度的上升，其优越性逐渐明显。尽管在分割速度上略有下降，但对于噪声干扰下的森林冠层图像分割问题展现出较高的精确性。其分割结果见图4。

3 结论与讨论

本研究提出了基于DE-WOA优化算法的多阈值图像分割方法，并应用于森林冠层图像分割研究。首先研究了标准WOA算法的仿生机制与搜索过程；然后针对标准WOA算法存在的局限性将DEA算法嵌入其中改进局部搜索策略，并提出以种群适应度为评价指标的混合策略来平衡混合算法的探索与开发；最后结合多阈值Kapur熵分割方法对最优阈值进行迭代搜索。为了验证所提混合算法的有效性，选用光线与复杂结构干扰下的森林冠层图像进行分割试验，并与PSO算法、WOA算法的分割结果在适应度值、PSNR、SSIM与计算时间等评价指标下进行对比分析。结果表明，DE-WOA算法可以获得更精确的分割阈值和更高的分割精度，在6阈值试验时，PSNR值较PSO、WOA算法分别提升0.230、0.235 dB，SSIM值提升0.539、0.536，为复杂森林冠层图像的分割提供了有效的方法。尽管在分割速度上相比其他算法较慢，但随着图像干扰带来的计算维度上升，DE-WOA算法在分割精确度上

的优势更加明显。在未来，将会深入研究更高效的算法及算子引入方式，在保证分割精度的前提下降低计算时间。