基于高光谱的石楠叶片叶绿素含量估算模型

何桂芳，吴 见，彭 建，谷双喜

(滁州学院 地理信息与旅游学院，安徽 滁州 239000)

叶绿素作为植物进行光合作用的主要色素，其含量与光合作用能力、植物胁迫以及健康状况关系密切[1]。快速、准确地掌握植株叶绿素含量，对于植物生长状态监测、产量预测、生境的适宜性评价等都具有非常重要的意义[2]。检测叶片叶绿素的常用方法有分光光度计法、原子吸收法、高效液相色谱法等，这些方法不仅具有破坏性，而且繁琐，还只能测有限样本[3]。高光谱分析技术具有快速、无损、成本低的优点，能直接对植被进行微弱光谱差异的定量分析[4]。因此，国内外有很多学者借助高光谱对叶绿素含量进行估算。目前，高光谱估算叶绿素含量的研究主要有2类：第1类使用原始光谱及各种变换光谱对叶片叶绿素含量进行估算。冯海宽等[5]、黄慧等[6]、李媛媛等[7]、胥喆等[8]对原始光谱、倒数之对数、一阶微分和连续统去除等变量，尼加提·卡斯木等[9]利用反射率、吸收深度等光谱参数，邓小蕾等[10]利用原始光谱及一阶微分的小波包去噪光谱等构建叶绿素反演模型。这类研究都是对单个敏感波段的光谱进行建模，精度可能会在一定程度上受到制约。第2类使用任意2波段构建的植被指数对叶绿素含量进行估算。何彩莲等[11]、姜海玲等[12]直接使用已经发表的固定波段的植被指数，Tumboetal[13]利用比值植被指数，程志庆等[14]利用归一化植被指数，孙红等[15]利用差值植被指数，武旭梅等[16]、罗丹等[17]利用比值、差值、归一化植被指数及土壤调节指数，陈秀青等[18]、王鑫梅等[19]用原始光谱、一阶导数的归一化差分和比值植被指数，马文勇等[20]、刘文雅等[4]、李春等[21]利用红边位置植被指数，构建SPAD 估算模型。这类研究使用的反演方法主要有随机森林、偏最小二乘、线性回归、BP神经网络、主成分分析、支持向量机等，根据自变量和因变量的个数选用合适的反演方法，都能够得到较高的精度模型。因此，利用高光谱分析技术对植被叶片叶绿素含量估算是可行可靠的，只是针对不同的植物和不同反演方法所选用的最佳波段和最佳估算变量不尽相同[22]。

以往研究大多集中在水稻、玉米、小麦等农田经济作物和苹果等果蔬上,对于园林绿化常用的绿色植物研究较少，本研究选取具有观赏和药用价值的常绿阔叶灌木石楠(Photiniaserrulata)为对象，通过实测光谱反射率和叶绿素含量，选择叶片尺度的原始光谱及4种变换光谱和差值型、比值型、归一化值型的6种常用植被指数，采用逐步线性回归和偏最小二乘方法建立叶绿素含量的高光谱反演模型，并对比单波段构建的模型与植被指数回归模型，寻求叶绿素最佳反演模型，为实现高光谱技术快速、大面积监测绿色植物的长势和营养监测提供理论依据和技术支撑，为园林绿植的养护和管理提供参考。

1 材料与方法

1.1 数据采集与处理

研究区为滁州市琅琊山景区，采集健康成熟的单株石楠叶片，在每棵树上采集3片叶片，并将叶片编号后同时进行光谱与叶绿素含量的测量。叶片光谱值采用美国ASD Field Spec光谱仪实测获取，波长350～2 500 nm，采样间隔为1 nm，共有2 150个波段。每个样点光谱数据记录8次，取每个样点的8条光谱数据平均值，作为该样点的光谱数据。叶绿素测定采用SPAD-502叶绿素仪，该仪器采用光电无损检测方法测得的SPAD(soil and plant analyzer development)值与叶绿素含量具有很高的相关性，常用于表征叶绿素含量[23]。选择晴朗的无风、无云天气9：00-11:00，先按照说明对仪器校准后，再对每片树叶的叶尖、叶中和叶基3个部位测量叶片光谱，同时在该样点上进行SPAD值测量。

分别对每一片树叶3个样点的SPAD值与光谱数据取平均值，作为该叶片的SPAD值与对应的光谱反射率。研究共测得59份叶片样本，随机选取40份作为建模样本，剩余19份作为验证样本。各类型样本的SPAD值统计特征见表1。其中，建模样本的SPAD值为3.70～50.00，区间分布合理，变异程度较大，能保证所建模型的适应范围；验证样本和建模样本的统计特征相差不大，能够验证模型的可靠性。

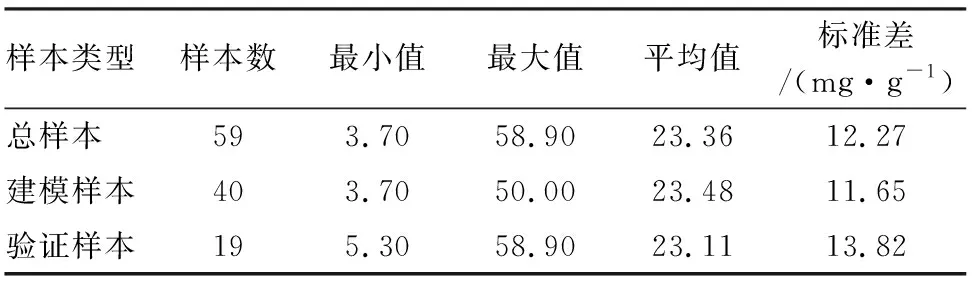
表1 SPAD值的统计特征

1.2 研究方法

1.2.1 光谱变换 在原始光谱反射率(reflectance,R)的基础上，计算其倒数1/R，倒数之对数(logarithm of reciprocal,LR，公式中用LR表示)、一阶微分(first order differential of reflectance,FDR，公式中用FDR表示)、二阶微分(second-order differential of reflectance,SDR，公式中用SDR表示)4种指标，计算公式见式(1)-式(3)。原始光谱经过LR变换后能够减少因为光照条件变化引起的乘性因素的影响，经过FDR变换后可以消除背景噪声的干扰，分解出混合的重叠峰，从而提高光谱的分辨率和灵敏度，找到相关性更高的波段。

LR=ln(1/R)

(1)

FDR=(Ri+1-Ri-1)/2Δλ

(2)

(3)

式中：Ri-1表示上一个波段的反射率，Ri+1表示下一个波段的反射率，R′表示一阶微分，Δλ为采样间隔。

1.2.2 植被指数 光谱的植被指数是2个或者多个波段光谱反射率的组合。通过对估算叶绿素模型的植被指数进行分析，选取6个常用植被指数[16]：比值指数(ratio vegetation index,RI，公式中用RI表示)、差值指数(difference vegetation index,VI，公式中用VI表示)、归一化指数(normalized difference vegetation Index,NDVI，公式中用NDVI表示)、光谱反射率一阶微分比值指数(ratio index of derivative,DRI，公式中用DRI表示)、光谱反射率一阶微分差值指数(difference vegetation index of derivative,DVI，公式中用DVI表示)、光谱反射率一阶微分归一化指数(normalized difference vegetation index of derivative,DNDVI，公式中用DNDVI表示)，植被指数公式见表2[24]。

表2 植被指数运算公式

1.2.3 逐步线性回归和偏最小二乘回归 逐步线性回归在构建方程时，先考虑自变量对因变量的作用显著程度大小，按照从大到小的原则逐个引入方程。每引入一个变量都将检验其显著性F，对不符合的变量进行筛选、剔除，确保每次引入新的变量之前方程中只含有显著性的自变量。逐步线性回归可以避免多元线性回归模型中的个别自变量贡献率较小的问题，筛选出显著性因子强的自变量[25]。偏最小二乘回归(partial least squares regression，PLSR)主要研究多因变量或单因变量对多自变量的回归建模，但是单因变量的偏最小二乘回归模型在日常分析中最为常见[12]。对于该方法的具体介绍可参考P.Geladietal[26]和S.Woldetal[27]。偏最小二乘回归适合变量个数很多且存在多重共线性同时样本数较少。在光谱建模过程中，PLSR能有效辨识光谱信息与噪声，降低光谱维数，减少数据冗余。PLSR的重点在于主成分个数的确定，主成分的个数会直接影响模型的稳健性，主成分个数过少会出现欠拟合情况，主成分个数过大会出现过拟合情况[28]。PLSR模型在SPSS中的实现过程参考王国华等[29]。

1.2.4 精度验证 模型构建与验证分析在SPSS23.0中完成，选用的模型精度验证的2个指标决定系数(coefficient of determination，R2)，均方根误差(root mean square error，RMSE，公式中用RMSE表示)，其计算公式：

(4)

(5)

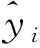
2 结果与分析

2.1 不同叶片叶绿素含量光谱曲线特征分析

对59个样本按照叶绿素含量进行升序排列，采用等间隔方法选取6个样本，其SPAD值分别为3.7、14.17、23.4、37.4、46.6、58.9，得到对应的6条原始光谱曲线(图1)。该曲线存在以下特征：1)波长350～500 nm，光谱反射率区别较小；2)可见光波段500～760 nm，光谱反射率波动趋势变化较大，不同叶绿素含量的曲线峰值波段有所差别；3)在760～1 360 nm，光谱反射率达到最大值，曲线比较平稳，6条曲线趋于平行；4)650～700 nm存在明显的叶绿素吸收谷，1 360～1 470 nm存在明显的水分吸收谷，但是部分曲线的吸收深度和吸收面积存在差异。

2.2 相关分析

2.2.1 叶绿素含量和变换光谱的相关性分析 分别计算叶绿素含量与R、1/R、LR、FDR、SDR之间的相关系数，其相关性分析见图2。

在0.01显著性水平上，原始光谱R在560～720显著负相关，最大相关系数波长699 nm(r=-0.800 9)，峰值带宽较小；光谱倒数1/R在580～720显著正相关，最大相关系数波长700nm(r=0.766 2)；光谱倒数之对数LR与1/R曲线几乎重合，但相关性比1/R稍高，最大相关系数波长698 nm(r=0.804 4)；光谱一阶微分FDR消除了相邻波段的影响，相关性比R有所增强，相关性变化剧烈，最大相关系数波长747 nm(r=0.928 3)，其峰值带宽较大；SDR最大相关系数波长701 nm(r=0.894 1)，其峰值带宽较小。各种光谱反射率与叶绿素含量之间相关系数最大波长均在可见光波段。

在可见光波段350～760 nm，叶绿素含量与各种光谱反射率之间相关性有正有负，变化明显。其中，LR与1/R 2条曲线差异最小，部分重合。FDR、SDR的相关系数变化较大，在正负之间波动，与R的相关系数相比有所增加，说明FDR、SDR可以将R在可见光波段的叶绿素光谱吸收特征反映出来。在760～1 700 nm，R、LR与1/R 3条曲线趋于平缓，在1 400 nm左右的水分吸收带有少量增强，FDR、SDR 2条曲线变化仍然较大，相关性时正时负，在水分吸收带时变化较为明显。

对叶绿素含量与R、1/R、LR、FDR、SDR的相关系数进行显著性检验。在0.01显著性水平上的波段有：R的519～569、741～1 718 nm；1/R的583～719 nm；LR的518～719、740～1 518 nm；FDR的503～546、634～677、702～769、1 221～1 236 nm；SDR的527～567、575、604～760 nm。

2.2.2 叶绿素含量与植被指数相关性分析 研究了350～2 000 nm范围内任意2波段组合的6种植被指数与石楠(PS)叶片的叶绿素含量值的相关性。为突出显示最佳波段组合，利用MATLAB软件分析并制作相关性矩阵二维图(图3)，红色到蓝色表示高正相关到高负相关。

波长之间的相关分析表明，可见光波段(350～760 nm)的2个波段之间相关性相对较强，特别是红光波段相关系数最高。近红外短波阶段(780～1 100 nm)光谱数据冗余较多，近红外长波阶段相关性有所增强。对比不同植被指数，RI、VI、NDVI的敏感波段组合相似，DRI、DVI、DNDVI的敏感波段组合相似。对相关系数进行统计分析，挑选相关系数的最大绝对值所在波段作为特征波段。结果表明，RI的最佳波段组合为RI(R733,R944),相关系数0.952 6，VI的最佳波段组合为VI(R732,R980)，相关系数0.956 2，NDVI的最佳波段组合为NDVI(R732,R931)，相关系数0.952 4，DRI的最佳波段组合为DRI(R747,R1 464)，相关系数0.950 2，DVI的最佳波段组合为DVI(R747,R1 464)，相关系数0.944 8，

DNDVI的最佳波段组合为DNDVI(R645,R1 370)，相关系数0.936 9。

2.3 叶片叶绿素高光谱估算模型构建

2.3.1 基于逐步线性回归和PLSR的叶片叶绿素估算模型 在通过显著性检验的光谱曲线中，挑选相关系数为波峰或波谷的波段作为特征波段。在R曲线中，特征波段为615、630、664、699 nm；1/R曲线中，特征波段为546、560、593、631、659、700 nm；LR曲线中，特征波段为546、558、621、631、664、698 nm；FDR曲线中，特征波段为532、536、541、553、560、611、636、647、655、660、680、691、705、735 nm；SDR曲线中，特征波段为567、639、658、685、693、701、708、736 nm。

分别以各种形式光谱特征波段的反射率作为自变量，以叶绿素含量为因变量，在SPSS中构建逐步线性回归模型和偏最小二乘模型。构建逐步回归方程时，先进行共线性诊断，确保入选的自变量之间不存在共线性。设置入选条件为显著性F检验的概率值小于0.05。构建偏最小二乘模型时，根据潜在因子的方差解释比例，确定最佳的潜在因子数。为检验模型的可靠性和实用性，采用决定系数R2和均方根误差RMSE对模型进行评定，结果见表3。

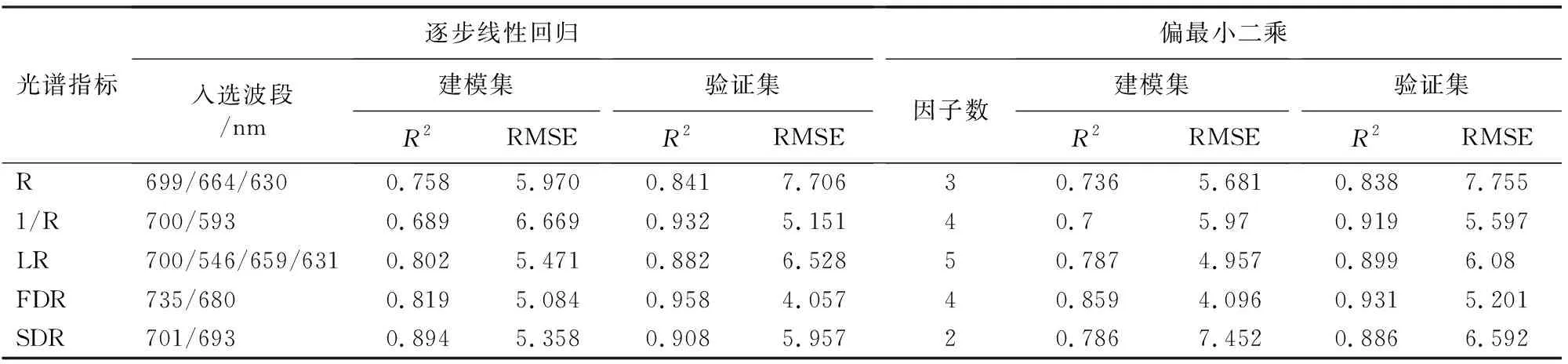
表3 基于原始光谱和变换光谱的叶绿素估算模型及精度

在叶绿素的逐步线性回归模型中，对R进行LR、FDR、SDR变换后，建模集和验证集的R2都变大了， RMSE都减小了，其中FDR变换的光谱对叶绿素含量预测效果最好。

在叶绿素的最小偏二乘模型中，基于变换光谱建立的模型较于原始光谱有效提高了反演精度，验证集的R2变大了， RMSE均减小，但是建模集的1/R、SDR变换后，2个精度指标变化不太一致，模型精度最高的仍然是FDR。从建模集的精度来看，R、SDR的逐步线性回归模型优于偏最小二乘模型。从验证集的精度来看，LR的偏最小二乘模型优于逐步线性回归模型。综合来看，最优模型为FDR的逐步线性回归模型。

因此，对R进行LR、FDR、SDR变换，能够提高叶绿素含量预测模型的精度和稳定性。

2.3.2 基于植被指数的单变量叶绿素估算模型 选择线性函数、二次函数、对数函数、逆函数、指数函数分别与6种植被指数拟合，构建叶绿素含量的单变量估算模型。通过比较决定系数R2和均方根误差RMSE，探索叶绿素含量的最佳单变量估算模型，结果见表4。

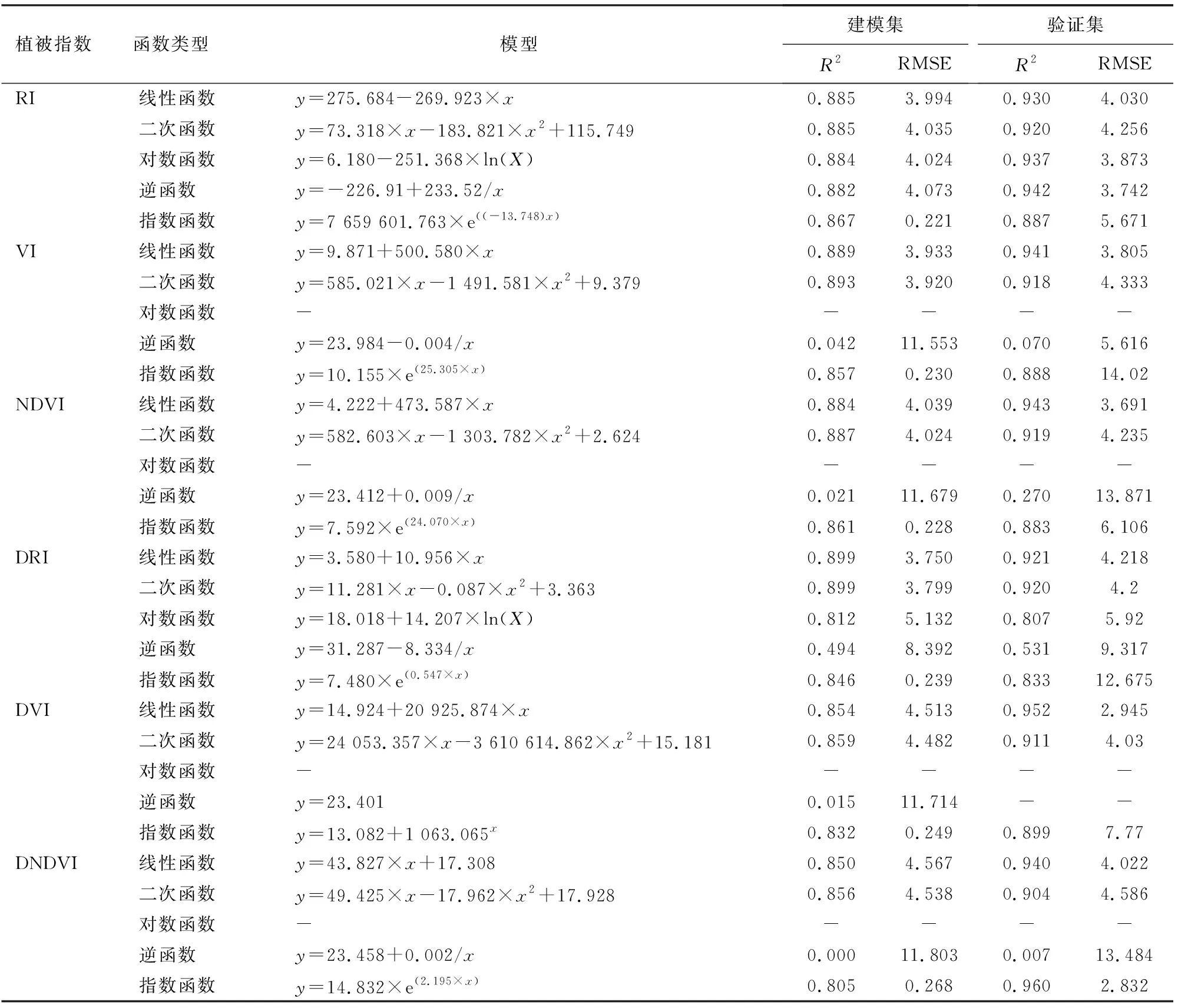
表4 SPAD的单变量拟合模型及精度

以上各种模型中，基于同一植被指数所建立的5种模型中，线性函数模型普遍具有较高的决定系数和较低的均方根误差，模型精度较高。二次函数模型的R2和RMSE都很接近。除了RI的逆函数R2>0.6外，其他几个逆函数的R2均小于0.6，表明逆函数不能进行叶绿素估算。对数函数与指数函数的R2和RMSE有的最好，有的较差。从建模集来看，精度最优的模型是DRI的线性模型，从验证集来看，最优的是DNDVI的指数模型。

3.3.3 基于植被指数的多变量叶绿素估算模型 以叶绿素含量为因变量，6种植被指数为自变量，在SPSS中构建逐步线性回归模型，并利用验证样本对建立的模型进行精度评价(表5)。

表5 基于植被指数的叶绿素估算模型及精度

逐步线性回归模型最终仅入选了DRI和RI 2个变量，其建模集的R2达到了0.93，说明模型预测效果非常高，RMSE为3.145，说明预测精度也很理想，同时检验精度也达到了0.955。

2.4 模型精度比较

依据上述分析，5种光谱指标的逐步线性回归模型和偏最小二乘模型的R2取值在0.700～0.958，预测精度最高为FDR的逐步线性回归模型。6种植被指数的5类函数模型中，除逆函数外，其余4类函数R2取值在0.8～0.96，预测精度最高为DNDVI的指数模型。6种植被指数构建的逐步线性回归模型最佳为DRI+RI，R2取值0.955。

为了直观展示叶绿素估算模型的拟合度和可靠性，绘制了预测值与实测值之间的1∶1关系图(图4)，可以看出基于植被指数DRI+RI的线性回归模型的样本点集中在1∶1直线的两侧，比单光谱指标和单植被指数模型的精度都要高。

3 结论与讨论

通过对入选波段的统计表明，石楠叶绿素含量相关性最高的波段在红波段(622～770 nm)；利用逐步线性回归和PLSR构建的各种变换光谱与叶绿素含量的预测模型结果具有一致性，光谱的一阶微分变换后能有效增强有价值波段信息，提高模型的精度；使用5种函数拟合的6种植被指数的预测模型中，仅RI的5种函数精度都较高，其他5种植被指数的对数函数和逆函数不能预测叶绿素含量；石楠叶片叶绿素估算最佳模型是RI和DRI的线性模型，说明比值植被指数比差值、归一化值植被指数有更好的预测能力。因此，本研究成果能为高光谱遥感技术在园林绿化中的应用提供依据。

对原始光谱与4种变换光谱构建叶绿素含量的逐步线性回归和偏最小二乘模型，发现基于FDR的逐步线性回归和偏最小二乘模型均最优。这可能与FDR消除了相邻波段的干扰有关，使得光谱的吸收特征信息被释放，相关系数最大值提高了0.13，从而改善了模型精度。由于R、1/R、LR、SDR入选的特征波段有限，使得其偏最小二乘模型精度低于逐步线性回归，而FDR构建的偏最小二乘模型精度与逐步线性模型较为接近，这可能与其入选特征波段较多有关。从试验结果分析可知，偏最小二乘模型更适合变量多且变量间存在较大共线性的情况，今后可尝试用所有显著性波段构建该模型。

6种植被指数与叶绿素含量间具有极显著相关性，最大相关系数都大于0.93，均高于原始光谱及变换光谱。研究表明，逆函数和对数函数只适用于RI，线性、二次、指数函数适用于6种植被指数，且6种植被指数构建的逐步线性回归模型中，RI(R733，R944)和DRI(R747，R1 464)2个变量建立的模型精度优于单植被指数变量模型。说明多个植被指数结合也可以提高叶绿素含量的估算精度。