内蒙古苏木山华北落叶松人工林生长模型研究

摘要：  在苏木山不同林龄华北落叶松人工林设置27块标准地，应用2种生物量模型W=a（D2H）b和W=aDb对各器官生物量和总生物量进行拟合，经比较分析发现，W=aDb模型不仅方便而且拟合更好。运用对数模型、考尔夫方程、豪斯费尔德、理查德模型、坎派资和逻辑斯蒂方程6个常用的生长模型对胸径、树高进行回归分析，结果表明：胸径生长模型用考尔夫方程拟合最好，方程为Y=6.261×Exp（0.061/x-0.865） 、树高生长模型用考尔夫方程拟合最好，方程为Y=5.453×Exp（0.043 /x-0.828）。对上述模型的预估值与实测值做配对样本t检验，sig>0.05差异不显著，预测模型的标准误差、平均绝对百分误差、平均百分误差、平均相对误差都很小，进一步证明预估计值与实测值没有显著差异，研究结果可为苏木山华北落葉松人工林生长预测提供依据，为林区的科学管理提供参考。

关键词：  华北落叶松;  人工林;  模型;  胸径;  树高; 生物量

中图分类号：   S 791. 22               文献标识码：   A                文章编号：1001 - 9499（2022）01 - 0026 - 04

华北落叶松（Larix principis-rupprechtii）是我国华北地区山地针叶林主要建群树种之一，不仅适应性强、病虫害少且材质优良。苏木山林场是内蒙古自治区中西部地区最大的人工林场，不仅对于乌兰察布市生态建设具有重大意义，而且对于该地区能否如期实现碳中和具有较大影响。平均胸径、平均树高、生物量是评价森林生长状况的重要指标[ 1 - 3 ]，一些学者对不同地区华北落叶松胸径、树高、生物量、材积等生长模型进行了研究，但未见对乌兰察布市苏木山林场的相关报道。本研究通过研究苏木山林场不同林龄的华北落叶松生物量、胸径、树高生长模型，为苏木山华北落叶松人工林生长预测提供依据，旨在为林区的科学管理提供参考，进一步提高苏木山华北落叶松人工林的固碳能力。

1 研究区概况

苏木山林场地处内蒙古乌兰察布市兴和县南部，地理坐标40°26′53"～40°39′30"N、113°38′33"～

114°02′27"E，东与山西省天镇县、阳高县相邻，南与丰镇市红山林场毗邻，西北与兴和县张嗥镇、店子镇接壤，东西最长40 km，南北最宽12.5 km。当地群山环绕，地势险峻，起伏较大，地貌主体为中低山地，走向为西北向东南，年平均气温5.5 ℃，最低气温-29.5 ℃，最高气温33 ℃，无霜期110天，年降水量500 mm。土壤基带是栗钙土。研究区乔木层为华北落叶松纯林，林下植物以刺玫（Rosa davurica）、胡枝子（Lespedeza bicolor）、绣线菊（Spiraea salicifolia）为主。

2 研究方法

2. 1 标准地设置

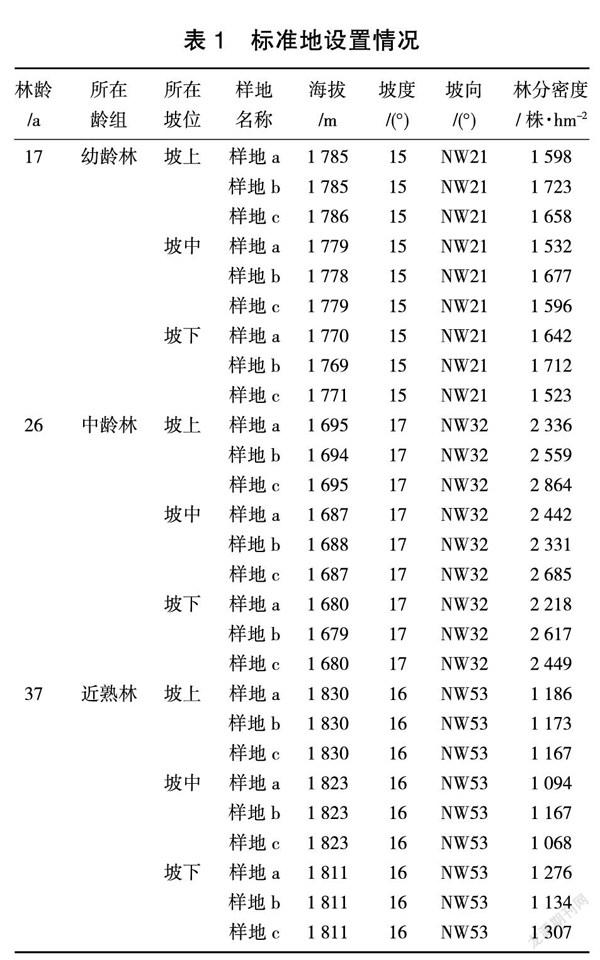
试验于2018年7月开始，2020年10月结束。研究区均为华北落叶松人工林纯林，在华北落叶松人工林纯林幼龄林、中龄林、近熟林中设置标准地，面积为20 m×20 m，不同林龄的林分在坡上、坡中、坡下各设置3块，总共27块标准地，详见表1。

2. 2 标准地调查及生物量计算

对27块标准地的华北落叶松进行每木检尺，测量其胸径和树高，分别计算每块标准地里所有乔木的胸径和树高平均值，将其作为该块标准地的平均胸径和树高。在每块标准地内选择1株标准木，要求此标准木与平均胸径和树高一致，采集全株干、皮、枝、叶、根（根采用整株挖掘）并测其鲜重，随后将上述样品各取500 g带回实验室，在烘箱85 ℃条件下烘干至恒重，根据样品占总鲜重的比例，计算各器官生物量及单株总生物量[ 4 ]。

2. 3 数据处理

2. 3. 1 模型建立

（1）华北落叶松单木生物量模型。应用国际和国内比较认可的2种生物量模型W=a（D2H）b和W=aDb对各器官生物量和总生物量进行拟合[ 5 ]，以林木单株各器官生物量及总生物量为因变量，林木胸径、树高为自变量，得出最佳生物量模型。

（2）华北落叶松单株胸径、树高模型。关于林木的生长过程，许多学者提出过不同的数学模型，一个理想的数学模型应该能够满足准确性高、使用性强的要求。为了准确描述华北落叶松的生长过程，本研究结合华北落叶松生长规律及根据以往研究经验和前人研究成果，主要选取了6种生长模型进行拟合[ 6 - 9 ]。公式如下：

对数模型： Y=A+B×Log（x+C）

考尔夫（ Korf） 方程： Y=A×Exp（-B/xC）

豪斯费尔德（Hossfeld）方程： Y=A/（1+B/xC）

理查德（Richards） 方程： Y=A×[1-Exp（-C×x）]B

坎派兹（ Gompertz）方程： Y=A×Exp[-B×Exp（-C×x）]

逻辑斯蒂（ Logistic）方程： Y=A/ [1+B×Exp（-C×x）]

式中，Y 为函数值（ 胸径、树高） 的总生长量;x为年龄;A、B、C为待求的参数; Exp 为自然对数底。

比较各模型拟合统计量，拟合优度检验采用R2（相关系数） 统计量和残差平方和（ SSE） ，其中残差平方和最小，相关系数最大的方程式作为最佳方程。

2. 3. 2 模型验证

对选出的生物量、胸径、树高模型进行配对样本t检验，并计算标准误差、平均绝对百分误差、平均百分误差、平均相对误差，判断实测值与预估值是否有显著差异。

3 结果与分析

3. 1 不同林龄华北落叶松胸径、树高及生物量

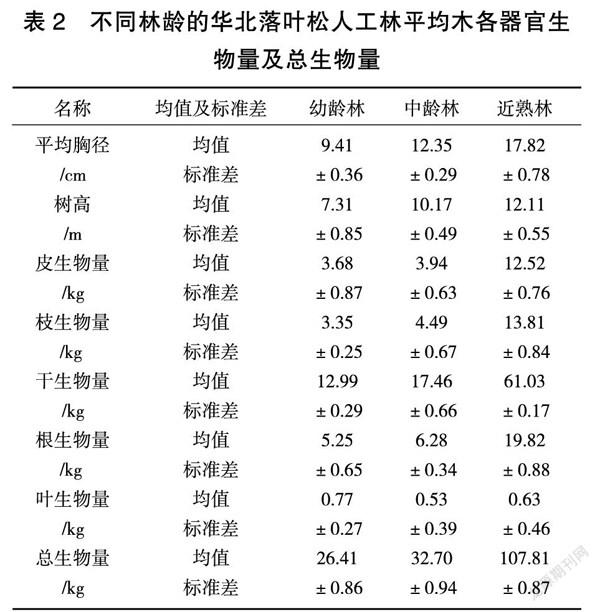
不同林龄华北落叶松人工林的平均木生物量随林龄的增大而增加，各器官的生物量及总生物量详见表2。

3. 2 华北落叶松单株树高、胸径与各器官生物量的关系及生物量模型

对不同林龄华北落叶松胸径、树高与各器官生物量之间进行Pearson相关性分析，结果显示，华北落叶松的胸径、树高均与各器官生物量具有极显著的相关性，在0.01水平（双侧），因此可以用胸径、树高作为自变量建立生物量模型，详见表3、表4。

各器官生物量及总生物量模型的W=aDb、W=  a（D2H）b相比，W=aDb回归系数R2较高，残差平方和SSE较小，说明用W=aDb對生物量进行拟合，效果较好。在实际工作中，运用W=a（D2H）b模型时需要测量树高，树高测定不仅误差较大而且过程繁琐，而模型 W=aDb不需要测量树高，所以模型W=  aDb在实际工作中更方便。

3. 3 华北落叶松单株胸径、树高模型

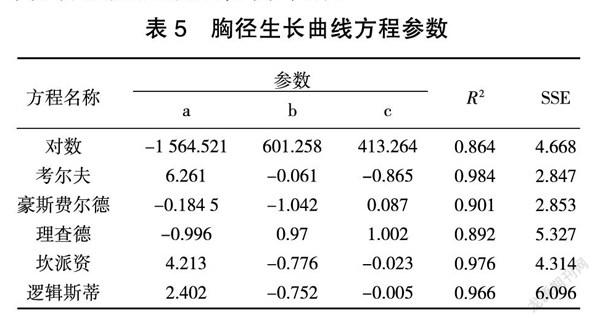
从胸径生长曲线方程参数（表5）可看出，6个胸径生长方程拟合的结果为考尔夫方程相关系数（R2） 最大，残差平方和（ SSE） 最小。根据相关系数最大、残差平方和最小的拟合方程是最优方程的原则，拟合胸径的最适合生长方程为考尔夫方程Y=6.261×Exp（0.061 /x-0.865），（R2= 0.984，SSE=2.847），式中：Y为胸径的总生长量，x为年龄。

从树高生长曲线方程参数（表6）可看出，6个树高生长方程拟合的结果为考尔夫方程相关系数（R2） 最大，残差平方和（ SSE） 最小，根据相关系数最大、残差平方和最小的拟合方程是最优方程的原则，拟合树高的最适合生长方程为考尔夫方程Y=5.453×Exp（0.043/x-0.828），（R2=0.998，SSE=0.053），式中：Y为树高的总生长量，x为年龄。

3. 4 模型检验

为了检验生物量模型、胸径、树高模型的预估效果，根据已知样木数据，将自变量代入模型，得出生物量、胸径、树高的预估值，结果见表7。通过配对样本t检验，对实测值和预估值进行检验，结果显示生物量、胸径、树高的sig>0.05差异不显著，预估模型标准误差、平均绝对百分误差、平均百分误差、平均相对误差都很小，进一步证明预估值与实测值没有显著差异，结果见表8。

4 结 论

对不同林龄华北落叶松胸径、树高、各器官的生物量及单株总生物量两两之间进行Pearson相关性分析的结果显示，华北落叶松的胸径、树高均与各器官生物量及单株总生物量具有显著的相关性，因此可用胸径、树高作为自变量来建立各器官生物量及总生物量模型，应用两种生物量模型W=a（D2H）b和W=aDb进行拟合，得出W=aDb模型不仅相关系数较大且操作更便捷，是研究华北落叶松各器官生物量及单株总生物量的首选模型。

根据相关系数最大、离差平方和最小的拟合方程是最优方程的原则，拟合胸径生长的最优方程为考尔夫方程Y=6.261×Exp（0.061/x-0.865），x为年龄;拟合树高生长的最优方程为考尔夫方程 Y=5.453×Exp（0.043/x-0.828），x为年龄。

经过配对样本t检验及误差分析，表明实测值和预估值差异不显著，模型能较好地预估华北落叶松生物量、胸径、树高。

5 讨 论

近些年，对华北落叶松生物量、胸径、树高生长模型的研究报道较多，本研究得出的生物量模型W=aDb模型与付晓燕对塞罕坝机械林场华北落叶松生物量的研究结果相同[ 5 ]，李大林采用指数函数、幂函数、逻辑斯蒂函数对燕山山地华北落叶松生物量进行研究。本研究得出胸径和树高生长模型均为考尔夫方程，严风翔认为对数模型和理查德模型拟合大青山华北落叶松胸径、树高更好[ 8 ]，原因可能是不同研究地区的环境及林分生长状况所致，当然不排除其他影响因素，今后需进一步研究。

本研究建立的生物量、胸径、树高生长模型能较好地预估苏木山华北落叶松林生长量，各模型的相应参数具有一定的生物学意义，可为苏木山华北落叶松人工林生长预测提供依据，为林区的科学管理提供参考。

参考文献

[1] 赵匡记，  王利东，  王立军，  等.  华北落叶松蓄积量及生产力研究[J]. 北京林业大学学报， 2015（2）：  24 - 31.

[2] 李大林，  姜鹏，  王玉峰.  燕山山地华北落叶松单株生物量与生产力研究[J].  河北林果研究， 2011（4）：  334 - 339.

[3] 马小欣，  姜鹏，  马娇娇，  等.  沿坝地区华北落叶松胸径-树高生长模型的研究[J].  林业资源管理， 2015（1）：  44 - 48.

[4] 赵敬，  康峰峰，  韩海荣，  等.  山西太岳山31年生华北落叶松人工林碳汇功能的研究[J].  干旱区资源与环境， 2016（10）：  110 - 115.

[5] 付晓燕，  江大勇，  王丽华，  等.  塞罕坝机械林场华北落叶松生物量研究[J]. 河北林果研究，2015，  30（2）：  113 - 116.

[6] 付小勇.  云南松林分生长模型研究[D].  昆明：  西南林学院， 2006.

[7] 姜立春，杜书立.  基于非线性混合模型的东北兴安落叶松树高和直径生长模拟[J]. 林业科学研究， 2012（1）：  11 - 16.

[8] 严风翔.  内蒙古大青山华北落叶松人工林生长模型研究[J].内蒙古林业科技， 2013（4）：  1 - 4.

[9] 李慧婷.  青海华北落叶松林直径结构及生长模型研究[J]. 福建林业科技， 2018（2）：  91 - 97.

第1作者简介：  田稼穑（1987-），  女，   高级工程师，  硕士研究生，  主要研究方向：  林业资源经营与管理。

收稿日期： 2021 - 12 -  03

（责任编辑：   王 岩）