基于TOPSIS的改进双层多目标优化算法研究
叶 茂,王 鲁*,马志东
(山东农业大学信息科学与工程学院,山东 泰安 271018)
1 引言
双层多目标优化问题是指在一个多目标优化问题中存在两个不同的决策者(DM),两个决策者位于不同的层级,并且独立控制着一组决策变量和相互冲突的目标函数。在双层多目标优化问题中,上层决策者(ULDM)先进行决策,下层决策者(LLDM)的决策受上层决策者的影响[1]。双层多目标优化问题的基本概念是首先由ULDM设定目标并做出决策,然后LLDM在ULDM的决策下对目标进行最优化计算,最后ULDM参考LLDM提出的方案综合考虑上下层,得到双层多目标优化问题的满意解。
TOPSIS(Technique for order performance by similarity to ideal solution)是解决多目标决策问题的经典方法之一,为多目标优化问题提供一个更广阔的折中方案。它的基本思想是所选结果与正理想解(PIS)距离最近,与负理想解(NIS)距离最远,将双层多目标优化问题中每一层中互相冲突的多个目标的转化为两个目标,即与PIS距离最近和与NIS距离最远[2]。然后利用模糊集理论中的隶属度函数来表示两种距离的满意度,最后利用FGP(fuzzy goals programming)方法解决两个目标相互冲突的问题[3],[4]。
近年来,双层多目标优化问题得到广泛的研究[5]。TOPSIS是由Hwang和Yoon首先提出,Lia等人将TOPSIS方法进行扩展用于求解双层多目标优化问题[6],[7]。Dey等利用线性化技术将非线性隶属函数转换成等价的线性隶属函数,然后进行归一化处理,接着建立模糊规划模型,通过最小化负偏差变量来实现问题的折中解[8]。Abo-Sinna利用TOPSIS方法求解分式规划问题,将目标函数转化为最大化型非线性函数,避免决策过程中出现的决策僵局[9]。Elsisy等人将TOPSIS方法和KKT(Karush-Kuhn-Tucker)结合用于求解模糊粗糙双层多目标线性规划问题[10]。El sayed对模型中分数目标的系数和标量进行模糊处理,避免问题中的舍入误差[11]。本文提出一种改进的双层多目标优化算法(MBLMOO),该方法结合TOPSIS方法和FGP方法,利用FGP方法代替TOPSIS方法中的最大最小模型,实验结果表明了该算法的有效性。
2 算法描述
2.1 问题阐述
双层多目标优化问题包含两个决策者,每一层都有一组不可通约、相互矛盾的目标函数[1][7]。双层多目标优化问题最大化型模型如下。
上层问题求解x1
(1)
下层问题求解x2

(2)
约束条件
x∈G={x=(x1,x2)∈Rn|
gi(x1,x2)≤0,i=1,2,…,q}≠∅
(3)
其中x1∈Rn1,x2∈Rn2,n=n1+n2,x1=(x11,x12,…,x1n1),x2=(x21,x22,…,x2n1),G为双层多目标优化问题的可行集,m1,i=1,2表示第i个决策者的目标函数个数,q表示约束函数个数。
2.2 基于TOPSIS的改进双层多目标优化算法
TOPSIS方法求解双层多目标优化问题的基本思想是所求的解与正理想解距离最近,与负理想解距离最远。方法中所提到的距离函数定义如下[9]
(4)

2.2.1 MBLMOO算法求解上层问题
针对双层多目标优化问题的上层问题
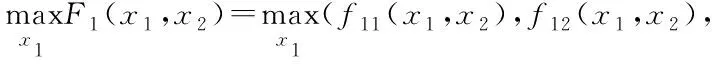
MBLMOO算法上层模型如下

(5)
s.t.
x∈G={x=(x1,x2)∈Rn|
gi(x1,x2)≤0,i=1,2,…,q}≠∅
(6)
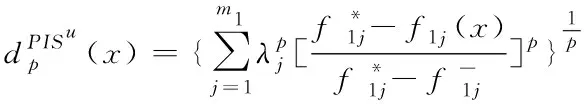
μ1(x)=

(7)
μ2(x)=
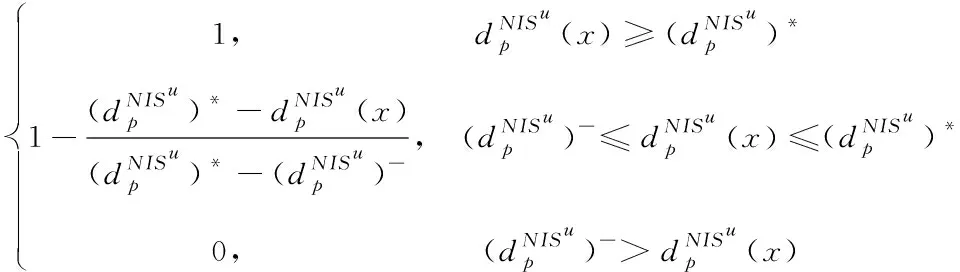
(8)
隶属度函数图像如图1所示。
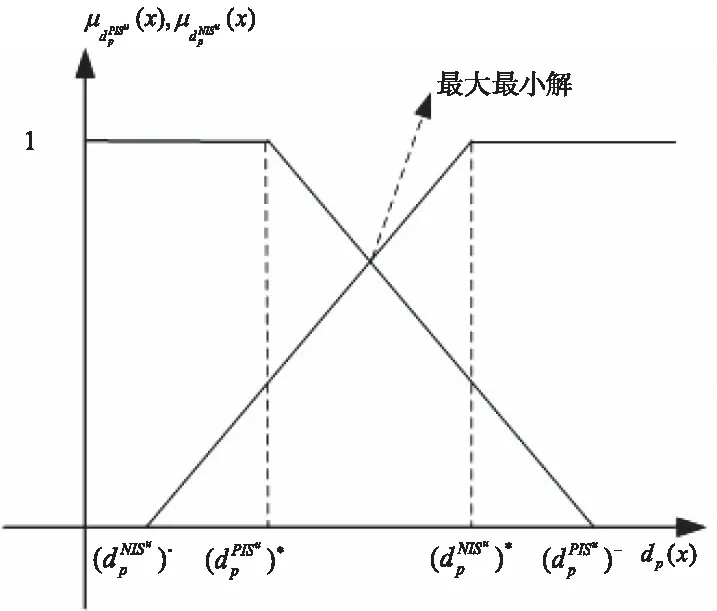
图1 隶属度函数μ1(x),μ2(x)
使用FGP方法[12]引入具有统一性适应度的成员目标如下
(9)
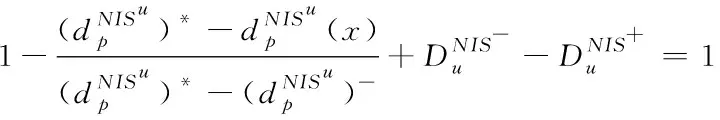
(10)

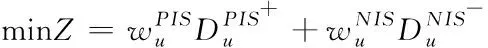
(11)
s.t.

(12)
x∈G={x=(x1,x2)∈Rn|gi(x1,x2)≤0,
i=1,2,…,q}≠∅
求解模型可得上层问题的决策向量x1u*=(x11u*,x12u*,…,x1n1u*),为了保证所提出的MBLMOO方法的有效性,将上层问题所得的决策向量作为下层问题的约束。
2.2.2 MBLMOO算法求解双层问题
为了使用基于TOPSIS方法得到双层多目标优化问题的满意解,构造双层问题的距离函数如下

(13)
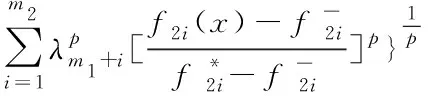
(14)
构造MBLMOO算法模型
(15)
s.t.
x∈G={x=(x1,x2)∈Rn|
gi(x1,x2)≤0,i=1,2,…,q}≠∅
(16)
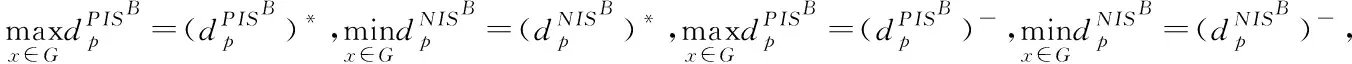
μ3(x)=

(17)
μ4(x)=

(18)
引入具有统一性适应度的成员目标如下

(19)

(20)
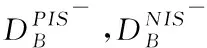
(21)
s.t.

(22)
x∈G={x=(x1,x2)∈Rn|gi(x1,x2)≤0,
i=1,2,…,q}≠∅
2.3 算法求解步骤
根据以上MBLMOO算法,算法步骤如下:
1)分别计算双层多目标优化问题各层中每个目标独立的最大值和最小值;
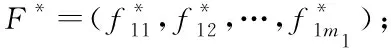

7)构造双层多目标优化问题的PIS和NIS收益表;
3 仿真研究
3.1 测试函数
通过求解Abo-Sinna[1]所研究的测试函数来验证所提出的MBLMOO算法的有效性。
上层优化问题
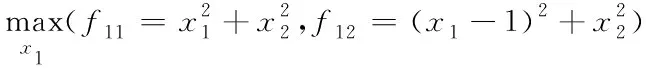
(23)
下层优化问题
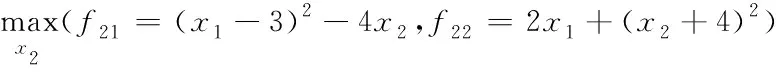
(24)
约束条件
x=(x1,x2)∈G={(x1,x2)|x1+x2≤4,x1,x2≥0}
(25)
对测试函数中每一个目标函数求解,其独立最优解的最大、最小值如表1所示。

表1 独立最优解的最大及最小值
3.2 MBLMOO算法求解测试函数上层问题
求解上层优化问题:

(26)
约束条件:
x=(x1,x2)∈G={(x1,x2)|x1+x2≤4,x1,x2≥0}
(27)
构造上层优化问题的PIS和NIS收益表如表2和表3所示:

表2 上层问题的PIS收益表

表3 上层问题的NIS收益表
s.t.

3.3 MBLMOO算法求解测试函数双层问题
下层优化问题:

(28)
约束条件:
x=(x1,x2)∈G={(x1,x2)|x1+x2≤4,x1,x2≥0}
(29)
构造下层优化问题的PIS和NIS收益表如表4和表5所示。

表4 下层问题的PIS收益表

表5 下层问题的NIS收益表
s.t.
使用Lingo程序求解模型,得到测试函数的满意解x*=(0,0.398),目标函数的解为f11=15.84,f12=16.84,f21=-6.92,f22=63.68,Z=1.877。
3.4 结果分析
将本文所提出的MBLMOO算法求解Abo-Sinna所研究的测试函数所得结果与Abo-Sinna提出的模糊方法[1]及A.Baky改进的TOPSIS方法[14]所求结果进行比较,各目标函数的最优解为f11=16,f12=17,f21=9,f22=64。比较结果如表6所示:

表6 比较基于不同方法的满意解及最优解
从表6中可以看出,MBLMOO算法得到的满意解与Abo-Sinna提出的模糊方法及A.Baky提出的TOPSIS方法所得到的满意解相比较,具有更好的表现。
4 总结
针对双层多目标优化问题的多层次多目标的特性,本文提出一种基于TOPSIS的改进双层多目标优化算法。利用TOPSIS方法的正理想解和负理想解的特性,将双层多目标优化问题中每一层中互相冲突的多个目标的转化为两个目标,然后利用模糊集理论中的隶属度函数来表示两种距离的满意度,并利用FGP方法解决双目标函数相互冲突的问题。最后通过一个测试函数与Abo-Sinna提出的模糊方法及A.Baky提出的TOPSIS方法相比较,结果验证了所提的MBLMOO算法的有效性。

