机器视觉图像分块像素点压缩方法仿真

傅建明，王冬庆

(1. 江西科技学院，江西 南昌 330098；2. 江西师范大学计算机信息工程学院，江西 南昌 330224)

1 引言

现阶段，多媒体领域对图像信息的存储和传输提出了更高的要求，也为现有的有限带宽带来了严峻的考验。高质量的数字视觉图像占用硬盘容量大，严重影响其存储和传输，图像压缩过程是解决此问题的关键性技术。因此图像压缩技术受到了越来越多的关注[1]。在此背景下，机器视觉技术[2，3]在图像中应用逐渐广泛，机器视觉图像压缩就是用最少的代码或符号表示出图像的主要信息和内容。但是在图像的压缩过程其质量会受到影响，导致图像细节信息丢失或特征模糊。

针对此问题，目前相关专家对图像压缩开展相应研究。郑铁[4]等人首先在单边高斯预测器的帮助下预测图像像素点以此消除图像的空间相关性，其次运用格型滤波器选取出各个谱带中的最优滤波器，从而生成预测误差，最终依据格型滤波器自身特性简化滤波器筛选经过，以此简化图像编码，完成图像压缩，实现机器视觉图像压缩。赵辉[5]等人首先构建正则化约束项构建优化模型，其次通过分裂Bregman迭代将图像压缩问题划分成多个子问题，获取每个子问题答案，并将所有问题答案结合生成最终的压缩结果，实现机器视觉图像压缩。

以上两种方法在图像压缩过程中忽略了对图像的分块预处理，导致图像的公共位图得出的结果不准确，极可能忽略部分像素点，存在压缩效果差以及峰值信噪比低的问题。为了解决上述方法中存在的问题，提出基于烟花算法的机器视觉图像分块压缩方法。

2 预处理

2.1 图像自适应分块

本文机器视觉图像压缩的前提是对图像分块压缩，为了确保压缩效果，利用图像的自适应方法进行分块[6，7]。

为了完美表示出机器视觉图像的纹理以及边缘等特征结构，同时也能很好地调控分块的复杂度，需要在图像稀疏变换[8]前计算出图像像素的灰度差值，并将其视为图像分块的依据，则图像像素灰度差的平均值计算公式为

(1)

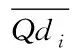
自适应分块算法[9，10]是通过四叉树算法实现的，即通过机器视觉图像的纹理变化将图像划分成等大的图像块，高效完成平坦区域和复杂区域的划分，从而得出机器视觉图像的自适应分块，图像分块流程图如图1所示。

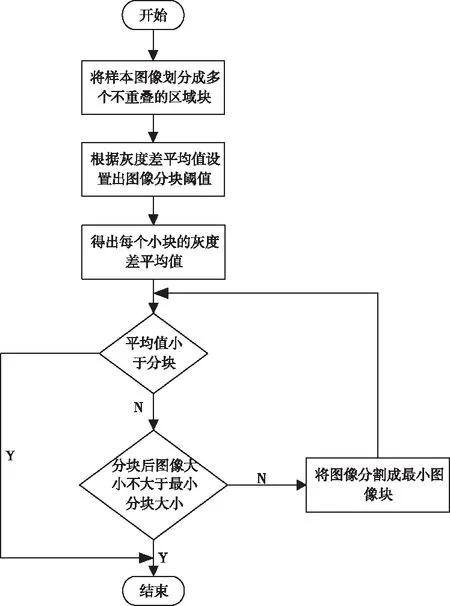
图1 机器视觉图像自适应分块流程

根据图像分块流程图可知，分块过程中需要计算出分块阈值，将分块阈值标记为P，由于P是由机器视觉图像中邻近像素点之间灰度差平均值得出的，则表达式为

(2)

基于图1的流程，结合式(1)和式(2)完成图像的自适应分块。

2.2 最优公共位图获取

利用BTC方法处理分块图像的R、G、B通道，生成位图Ro、Go和Bo，则机器视觉分块图像中位于点(i，j)的初始公位图元素点的表达式为

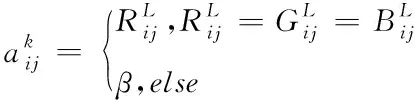
(3)

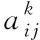
将初始公共位图AM的元素β集合生成向量S，其表达式为

S=(β1，β2，…，βN)

(4)

根据式(3)和式(4)即可计算出初始公共位图AM，为了生成最优公共位图，需要提前对向量S进行初始化处理[11]，为保证初始化后的向量S不会对其余元素产生影响，只能选用W-plane算法完成初向量S的初始化处理，通过对子图像的预处理得出最优公共位图以此加强最终的压缩效果。

3 基于烟花算法的图像压缩

经过分块处理后的子图像每个像素点均存在对应的散射点，因此对分块机器视觉图像的压缩就即为对像素点的压缩，而位图就是由单个像素组成的，因此分块图像压缩实质上就是对位相的压缩。

对分块图像预处理并生成初始化的向量S后，使用烟花算法优化向量S，进而获取相应的位图以及量化值，在烟花算法[12，13]中通过均方误差[14]得出所需评价函数，进而求解出烟花算法的适应度值，其计算公式为

H(Xi)=

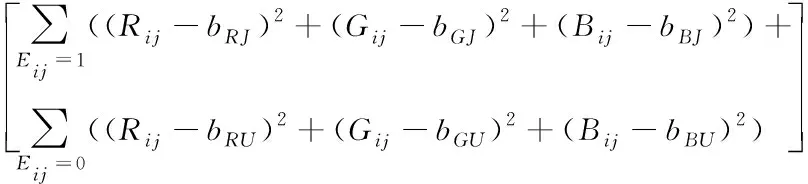
(5)

式中，U和J均代表公共位图元素的位置标记，Xi代表烟花个体，Eij代表烟花个体相应的位图在点(i.j)的值，bRJ、bGJ、bGJ、bRU、bGU和bBU均代表烟花个体相应的量化值，Rij代表分块图像权重与通道R在点(i.j)处的灰度值，Gij代表分块图像权重与通道G在点(i.j)处的灰度值，Bij代表分块图像权重与通道B在点(i.j)处的灰度值。

烟花算法在开始计算前需要将烟花种群进行初始化处理，则初始化后的烟花种群表达式为

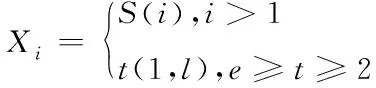
(6)

式中，t(1，l)代表维度为l的二进制向量，e代表初始化的烟花数量。

经过初始化处理后的烟花种群即可将烟花根据行数进行排列得出完整的位图Eh，进而求解出各个烟花相应的量化值，其表达式为

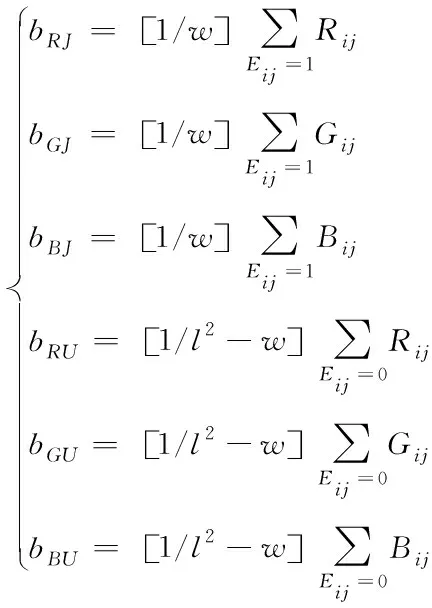
(7)

式中，w代表位图Eh值为1的元素数量。

根据式(5)计算出的适应度值，求解出各个烟花的爆炸火花个数以及爆炸半径，其计算公式分别为：

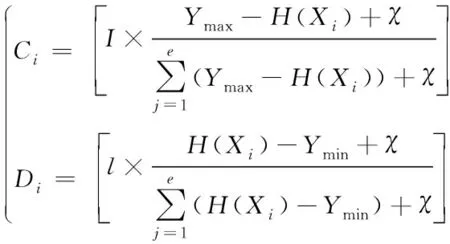
(8)

式中，I代表固定常数，χ代表机器视觉的最小量，Ymax代表适应度的最大值，Ymin代表适应度的最小值。

烟花算法中对于每个烟花来说其爆炸范围的数量以及爆炸半径任意生成的，从而得出爆炸范围的火花元素计算公式为

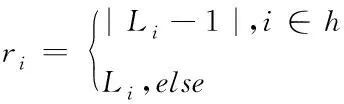
(9)

其中，h代表烟花算法的爆炸范围，ri代表爆炸火花点在点i处的元素，Li代表烟花个体在点i处的元素。

根据式(9)即可获取爆炸范围内的爆炸火花。

高斯变异火花的获取也必须提前计算出每个烟花中高斯变异火花各处的元素值，其计算公式为

qi=|Li-1|

(10)

式中，qi代表高斯变异火花点i的元素值。

根据式(9)和(10)得出爆炸火花以及高斯变异火花，在烟花以及上述两种火花中选取出适应度最小的火花视为新生代烟花种群。

不断重复上述步骤，直到完成迭代，将适应度最小的烟花视为向量S的最优值，在最优向量S上得出与之对应的完整位图以及6个量化值，进而得出效果最佳的压缩图像。

经过烟花算法的机器视觉图像压缩仅仅是针对位图的压缩[15]，因此还需要将分块图像进行重构[16，17]，在完整位图以及6个量化值的帮助下得出子图像块的重构公式为

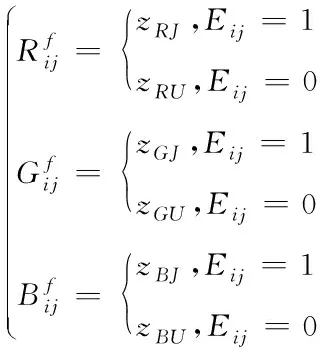
(11)

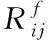
通过以上步骤完成机器视觉图像的分块像素点压缩。

4 实验结果

为了验证基于烟花算法的机器视觉图像分块压缩方法整体的应用性能，采用提出方法、文献[4]提出的基于格型递归最小二乘滤波器组的高光谱图像压缩方法以及文献[5]提出的基于结构组全变分模型的图像压缩方法设计对比实验，完成压缩效果以及峰值信噪比的仿真测试，测试结果如下所示。

4.1 压缩效果主观对比

机器视觉图像压缩可以在保证图像数据完整的基础上占用最小的系统空间，所以经过压缩后的图像较原图像对比其图像清晰度较低，但压缩过强会导致图像数据不完整，根据这一标准，随机选取一幅机器视觉图像，利用提出方法、文献[4]提出的基于格型递归最小二乘滤波器组的高光谱图像压缩方法以及文献[5]提出的基于结构组全变分模型的图像压缩方法对实验图像实现压缩方法，现已知三种图像的压缩比例一致，将三种方法的压缩结果进行比较，清晰度越高即内容数据越完整，即压缩效果最好，实验结果如图2所示。

图2 不同方法的图像压缩效果对比

根据图2的不同方法处理结果可知，提出方法压缩后的图像清晰度没有发生改变，这主要是因为该方法在图像压缩过程中对图像实现了预处理，保证公共位图的计算精度，进而确保压缩过程中不会遗漏任何像素点，从而保证图像的信息完整，以此优化了图像压缩效果。文献方法经过压缩后的图像清晰度均有所降低，这是因为图像经过重新编码和重构将多余数据和色彩等无用排除，仅仅留下必要数据导致的。

4.2 峰值信噪比对比

峰值信噪比RPSN是衡量图像压缩性能最有效的指标之一，压缩图像的峰值信噪比可直接反映出压缩图像的逼真度，进而高效评价出图像质量，峰值信噪比的公式如下所示

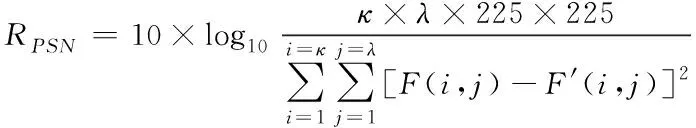
(12)

式中，κ代表压缩图像的行向像素点数量，λ代表代表压缩图像的列向像素点数量，F(i，j)代表原始图像在点(i，j)的分辨率值，F′(i，j)代表压缩图像在点(i，j)的分辨率值。

由于部分压缩后的图像无法用人眼识别图像压缩的好坏，此时可用峰值信噪比RPSN进行评价，峰值信噪比RPSN实质上是在客观的角度，衡量原始图像以及压缩后图像的逼真程度，通常情况下逼真度较好时峰值信噪比RPSN均大于30dB，当压缩后的图像RPSN越大，则说明图像清晰度越高，即保证压缩要求的情况下与原始图像越相似。在同一实验环境下利用三种方法对多组图像进行压缩，且每张图像的质量和像素点均不相同，通过式(12)计算出每种方法压缩结果的峰值信噪比，从而得出最佳压缩方法，实验结果如表1所示。

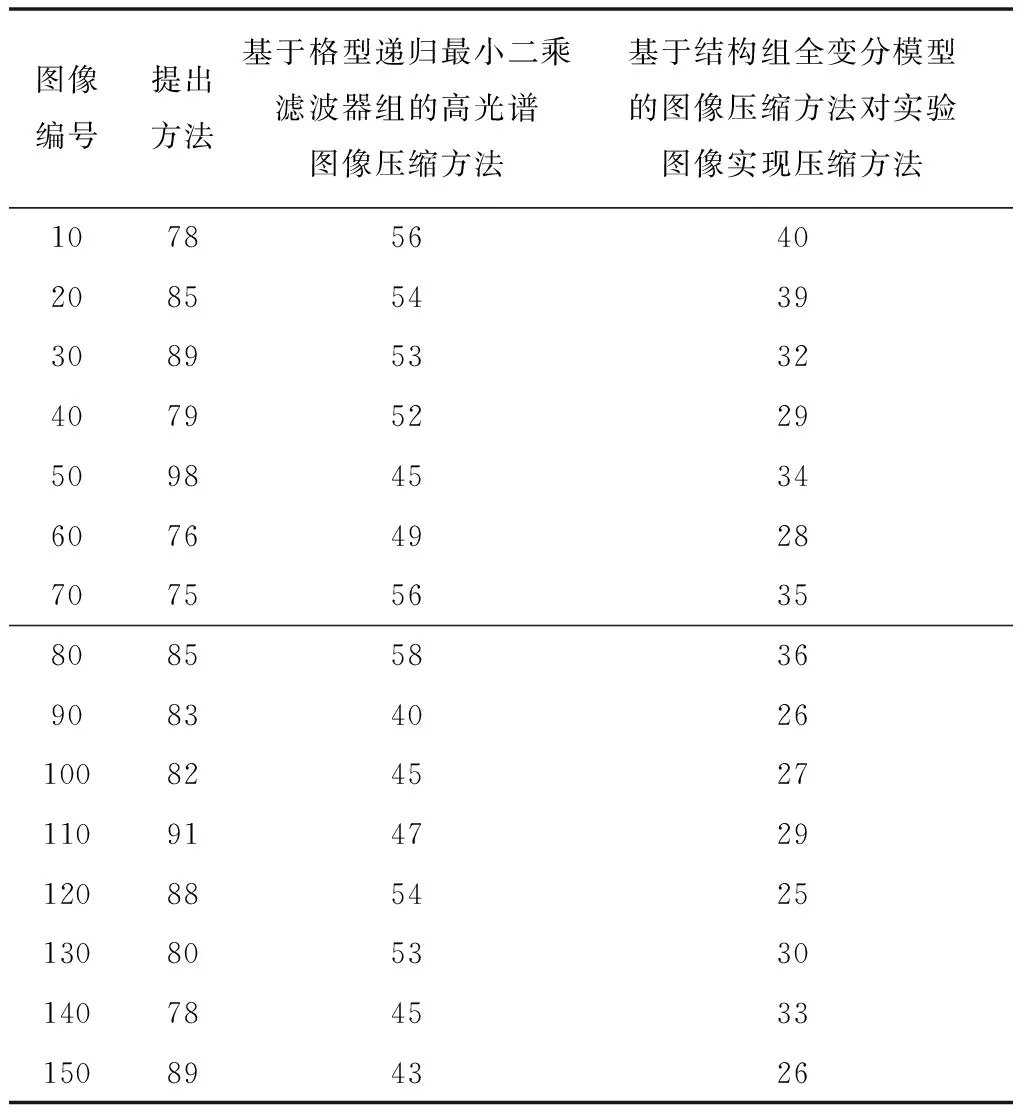
表1 三种压缩图像方法应用下的峰值信噪比/dB

根据实验结果可知，提出方法下的每组实验图像其峰值信噪比均远远大于30dB，说明提出方法压缩后的图像清晰度较高，本文压缩图像信噪比与其余两种方法相比均高出许多，而结构组全变分模型的图像压缩方法只有部分压缩图像的峰值信噪比大于30dB，说明该方法压缩效果不稳定，最终呈现的图像逼真度较低，从而证明了提出方法压缩性能强。

5 结束语

图像压缩可大大降低图像所需存储空间，但部分图像压缩后的会出现图像数据不完整等问题，为此，提出基于烟花算法的机器视觉图像分块压缩方法，对机器视觉图像分块预处理，在此基础上利用烟花算法对图像实时压缩处理，实现机器视觉图像分块压缩，解决了压缩效果差以及峰值信噪比低的问题，最大程度保留了图像信息。