考虑用户用电行为聚类的电力负荷预测方法
黄 薇,温 蜜,张照贝
(1. 国网上海市电力公司,上海 200122;2. 上海电力大学计算机科学与技术学院,上海 201303)
1 引言
智能电表快速普及使得电力企业掌握大量的用户细粒度用电数据,为分析用户用电行为特性提供了数据基础,电力企业可根据用户用电行为特性制定个性化售电政策[1]。同时智能电表数据为用户聚合体负荷预测提供了新视角,即根据用电行为特征将用户聚类为不同的用电群体,然后再针对每类用户建模分析以满足精细化电力负荷预测的需求[2]。
国内外研究者关于用户用电行为聚类的研究主要围绕特征提取和聚类算法两方面展开工作,按照输入特征的不同可分为直接、间接聚类方法[3]。直接聚类方法是使用原始负荷数据序列进行聚类分析,主要有K-means[4]、模糊C均值聚类[5]等算法。文献[6]使用动态K-means对用户用电行为聚类分析,解决了K-means需要预先设定聚类簇数的缺点。直接聚类方法主要用于跨度短的时间序列,在应用到跨度长的时间序列却存在收敛困难、算法复杂度高等问题。而间接聚类方法可在用户负荷序列上提取若干个用户用电行为特征,然后依据用户特征进行聚类分析并提取典型用电模式,有效地解决收敛困难以及算法复杂度高的问题。文献[7]使用主成分分析(Principal Component Analysis,PCA)方法提取用户负荷的行为特征,再使用K-means进行聚类辨识,结果表明PCA提取的特征可揭示用户用电行为。文献[8]提出基于互信息系数和相关系数的特征优选策略,该方法有效降低聚类过程中的算法复杂度。文献[9]在特征优选策略的基础上提出采用准确度和有效度确定聚类过程中的聚类簇数,并验证该方法的有效性。文献[10]首先从统计学方面解释选择中位数与平均数作为用户用电行为特征的合理性,再使用轮廓系数确定聚类簇数。以上文献在聚类过程中多采用统计学指标作为用电特征,而对用户用电负荷序列的动态性分析存在不足。
目前,关于用户侧负荷预测的研究主要是从用户聚合体负荷进行建模,而以用户用电行为聚类分析为基础的负荷预测研究处于初步阶段。文献[11]首先使用K-means算法对用户用电行为聚类分析,然后对各类用户建立预测模型,叠加各类用户负荷预测结果得到用户聚合体负荷预测结果,实验表明通过用户用电行为聚类可提高用户聚合体负荷预测精度。文献[12]通过谱聚类算法对用户负荷聚类,然后对各类用户建立预测模型以实现用户聚合体负荷预测。文献[11,12]主要为点负荷预测研究,而概率负荷预测方法可反映负荷的不确定性信息更受欢迎[13,14]。文献[3]采用三种概率预测方法对各类用户负荷预测,并求和得到用户聚合体负荷预测结果,仿真验证了该方法可提高用户聚合体负荷概率预测的精度。用户负荷具有较明显的波动性、随机性,而分位数回归森林算法采用并行集成预测可有效减少预测方差,可有效处理波动性较强的时间序列[15],但关于分位数回归森林(Quantile Regression Forest,QRF)概率算法在用户侧电力负荷预测上的应用较少。
综上分析,本文提出一种考虑用电数据序列动态性特点的用户用电行为聚类方法,并在用户用电行为聚类的基础上采用QRF建模以实现用户聚合体负荷预测。首先在第2节计算用户用电负荷的分位数自协方差表示用户用电行为特征,并采用层次聚类算法对用户用电行为特征聚类。然后在第3节使用QRF构建各类用户用电负荷的预测模型并将其结果叠加形成用户聚合体负荷预测结果。最后在第4节采用伦敦智能电表数据集进行仿真验证提出方法的有效性。
2 基于分位数自协方差的用电行为聚类方法
2.1 分位数自协方差
文献[16]提出使用时间序列的分位数协方差作为聚类特征,并证明该特征能够反映时间序列的动态性和数据之间的依赖性特点。为此。本文在分析文献[16]的基础上考虑使用分位数自协方差(Quantile autocovariance,QC)表示用户用电行为特征,QC的详细描述如下。
已知时间序列为{X1,…,Xn},其QC计算表达式如下所示
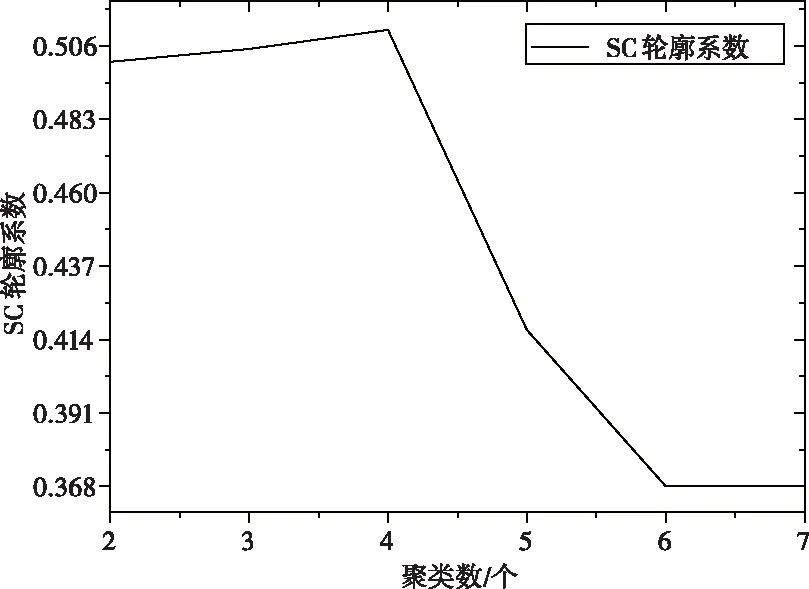
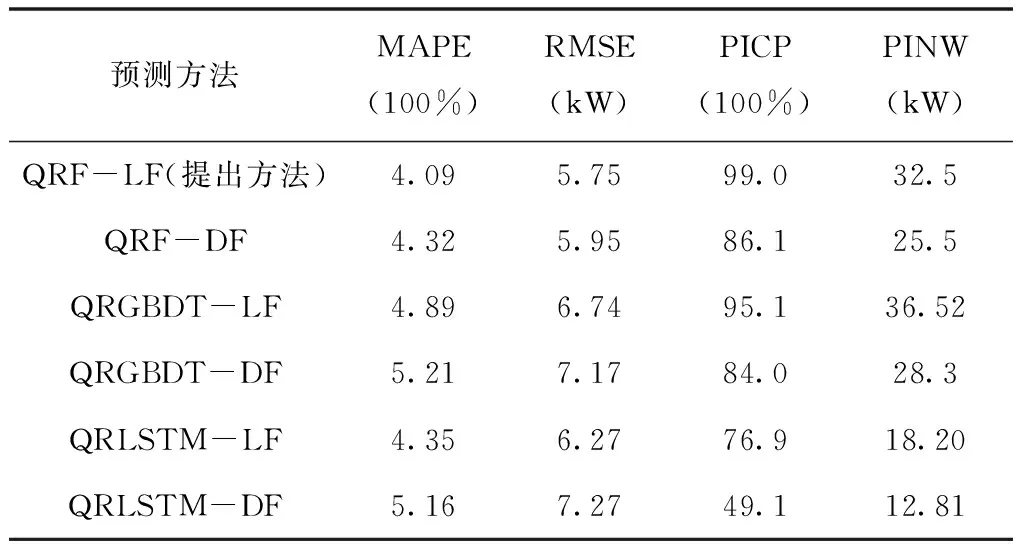
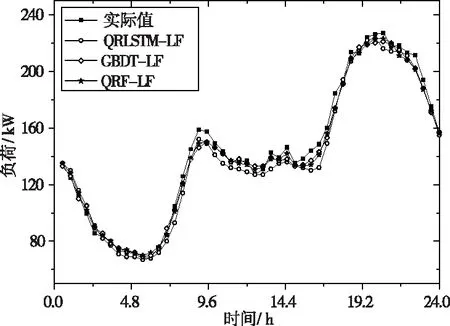
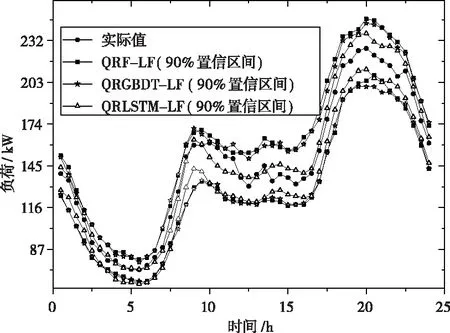
γ(τ,τ*)(t,t+j)=Cov(I(Xt (1) 式(1)中的γ(τ,τ*)(t,t+j)为时间序列在分位数τ∈(0,1)和τ*∈(0,1)下的自协方差,j为时间延迟。其中Cov(I(Xt Cov(I(Xt (2) 式(2)中τ和τ*为分位数,ττ*为完全耦合随机数。I(Xt (3) 式(3)中Xt为时间序列,ρτ(Xt,qτ)为弹球损失函数。 QC的参数有助于分析时间序列动态性特点,根据文献[16]的建议,选择参数j=1和τ∈{0.1,0.5,0.9},构造表达用户用电行为的9个特征如式(4)所示。 γ={γ(0.1,0.1),γ(0.1,0.5),γ(0.1,0.9),γ(0.5,0.1),γ(0.5,0.5),γ(0.5,0.9),γ(0.9,0.1),γ(0.9,0.5),γ(0.9,0.9)} (4) 层次聚类算法分为自上而下与自下而上两种聚类方式。其中,自下而上的方式首先根据用户QC计算用户之间的欧式距离,将距离相近的用户合并为一类。然后根据类与类之间的距离,将距离相近的类合并为较大的类,合并至设定聚类数目时则结束。采用层次聚类算法的原因为易于实现,且可体现用户与类别间的隶属关系。 在用户用电行为聚类过程中,聚类簇数设置过多使得用户用电行为共性表达不充分,过少则掩盖用户用电行为的差异性。为此,采用轮廓系数确定聚类数目。轮廓系数(Silhouette Coefficient,SC)是一种评价聚类结果的方式,其在类内聚合度和类间分离度两个方面反映聚类效果,某个用户的SC计算表达式如式(5)所示 (5) 式(5)中的S(i)为SC系数,其取值范围为[-1,1],S(i)=1表示类内聚合度和类间分离度均达到最优。a(i)为类内聚合度,表示用户i与类内所有用户的平均距离。b(i)为类间分离度,表示用户i与相邻最近一类内所有用户的平均距离,将所有用户的轮廓系数求平均值为聚类结果的轮廓系数。 提出基于分位数自协方差和层次聚类算法的用户用电行为聚类过程如图1所示。 图1 用户用电行为聚类流程图 用户用电行为聚类流程详细描述如下: Step1:数据预处理得到用户用电负荷序列数据{X1,…,Xn}; Step2:使用式(3)计算用户用电负荷数据在不同分位数下的最佳分位数值(q0.1,q0.5,q0.9); 图2 考虑用户用电行为聚类的电力负荷预测过程 Step3:使用式(1)计算各个用户用电负荷数据的分位数自协方差反映用户用电行为特征(QC); Step4:初始化最佳轮廓系数SC=-1和最佳聚类数为kB=2,令聚类簇数k=2并设定kmax的值; Step5:执行层次聚类并计算聚类结果的轮廓系数SCk; Step6:比较SCk>SC,若满足则更新SC和kB,否则执行Step7; Step7:令k=k+1并判断k>kmax,若满足则获得最终聚类结果。 由于用电用户数量多,若对单一用户建立预测模型,不仅存在计算量大的问题,而且不能有效捕捉用户用电行为特性等问题。为此,本文使用分位数回归森算法对各类用户子聚合体负荷建立概率预测模型以实现用户聚合体负荷预测。 分位数回归森林算法是将分位数回归与随机森林融合的算法,该算法可获得不同分位数下的预测值,并兼有随机森林模型参数影响小、运行速度快等优点[17-18]。QRF是适应性近邻分类与回归过程,对任意X=x,获得原始n个观察值的权重集合wi(x),i=1,2,…,n。QRF将所有因变量观察值的加权和作为因变量Y条件均值E(Y|X=x)的估计。QRF定义E(1{Y≤y}|X=x)的估计为观察值1{Y≤y}的加权平均,表达式如下所示 (6) QRF算法具体流程为: Step1:生成m棵决策树T(θt),t=1,2,…,m。对于每棵决策树每个叶节点,考察该节点所有观察值; Step2:给定X=x,遍历所有决策树,计算每棵决策树观察值的权重wi(x,θt),i=1,2,…,n。通过对决策树权重wi(x,θt),t=1,2,…,m取平均形成每个观察值i∈{1,2,…,n}的权重wi(x); Step3:对任意y∈R,通过Step2获得权重,再利用式(6)计算分布函数的估计。 提出的考虑用户用电行为聚类的电力负荷预流程如图2所示。该流程共3部分:用户子聚合体负荷形成、构造数据集、电力负荷概率预测。 3.2.1 用户子聚合体负荷形成 (7) 3.2.2 构造数据集 根据子聚合体负荷数据、时间信息等构造数据集,数据集中包含的数据特征及编码方式如表1所示。 表1 数据特征以及编码方式 由于构造数据集中的输入特征属于不同量级,为了减少数据量级对提出预测方法的影响,归一化处理数据。归一化公式如下式(8)所示 (8) 式(8)中:x为原始输入特征,xmax与xmin为原始输入特征的两个极值,xn为处理后的结果。 3.2.3 电力负荷概率预测 在各类用户构造数据集的基础上实现用户聚合体电力负荷概率预测。首先,将数据集划分为训练集、验证集、测试集;然后,使用训练集和验证集确定QRF概率预测模型最佳参数,并由各类用户的QRF概率预测模型得到不同分位数条件下的预测值;最后,叠加各类用户的分位数预测值,得到用户聚合体各分位数下的负荷预测值,其表达式如式(9)所示 (9) 采用伦敦智能电表数据集验证提出方法的有效性[19]。采用数据集中600户家庭用户、时间跨度为2013整年、采样周期为0.5h的电力负荷数据集作为实验数据集。数据集中的数据特征有“number”为用户编号,“date”为负荷数据采集时间,“data”为电力负荷数据。 在用户用电行为聚类过程中,为了确定最佳聚类数目kg,采用轮廓系数选择聚类数目k。不同k值的轮廓系数如图3所示。 图3 不同聚类数目的轮廓系数图 从图3中可看出,聚类数目为2、3、4时,轮廓系数变化相对平稳,然而当聚类数目为5时轮廓系数下降较为明显,故聚类数目宜选择为4。同时在聚类数目为4时,其轮廓系数为5.11达到最大值,故将聚类数目设置为4类。聚类后各类用电行为的用户数分别为155、372、55、18户,其各类用电行为的负荷箱线图如图4所示。 图4 各类用电行为的负荷箱线图 从图4中可看出,各类用户存在用电行为存在差异性,用电行为类别1有明显的用电爬坡期,用电高峰期持续时间较长。用电行为类别2有明显的两次用电高峰和低谷期特点,而用电行为类别3虽两次用电高峰和低谷期特点,但其持续时间较短。用电行为类别4的用电行为相对平稳。 在子聚合体负荷的基础上实现用户聚合体负荷提前12小时预测,数据集划分比例为80%的数据用于模型训练,10%的数据用于验证,10%数据用于测试。为了验证提出方法的有效性,设置对比预测方法有: 1)使用分位数回归森林算法建立用户聚合体负荷预测方法(QRF-DF); 2)使用分位数回归梯度提升决策树算法建立用户聚合体负荷预测方法(QRGBDT-DF); 3)使用分位数长短期记忆网络建立用户聚合体负荷预测方法(QRLSTM-DF); 4)使用本文提出的方法,预测模型采用分位数回归梯度提升树(QRGBDT-LF); 5)使用本文提出的方法,预测模型采用分位数回归长短期记忆网络(QRLSTM-LF)。 4.2.1 参数设置 提出的电力负荷预测方法中QRF的参数设置为:基学习器选择为树模型,基学习器的数量为200,树深度为12,损失函数使用均方误差。对比预测方法不是本文研究重点,其实验参数不在赘述。提出预测方法与对比预测方法均在python编程语言、Keras深度学习框架和sklearn库下实现,所有实验均在CPU为Intel Core i5-8250和内存为8GB的计算机上运行。 4.2.2 评价指标 为评估提出预测方法的有效性,采用平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)和根均方误差(Root Mean Square Error,RMSE)作为点负荷预测结果评价指标,其表达式如下所示 (10) (11) 采用区间覆盖率(Predict Interval Coverage Probability,PICP)和预测区间平均宽度(Predict Interval Average Width,PIAW)评价概率预测结果的可靠性。 (12) (13) 式(12)中:N为样本的总数目;ζn为布尔变量,如果电力负荷实际值落在预测区间的上下之间则ζn=1,否则ζn=0。式(13)中:Un为预测区间的上限;Ln为置信区间的区间下限。PICP和PIAW是一对矛盾体,其PICP值越高说明其置信区间可靠性越高,但在PICP相同时,PIAW较小时则预测效果越好。 4.2.3 结果分析 提出考虑用户用电行为聚类的电力负荷预测方法与对比预测方法在测试集上的预测结果如表2所示。 表2 不同预测方法效果对比表 从表2可以看出,提出的预测方法QRF-LF在MAPE和RMSE指标上获得最佳的效果,相比于QRF-DF分别提高0.23%和0.2kW,表明提出预测方法可提高用户聚合体负荷预测效果。QRF-LF在MAPE、RMSE指标上相比于QRLSTM-LF、QRGBTD-LF分别提高0.27%、0.52kW和0.8%、0.99kW,验证了QRF方法在用户侧负荷预测上的适用性。在PICP和PINW指标上可看出,QRF-LF方法在PINW指标上明显高于QRF-DF方法,表明QRF-LF方法预测效果更加可靠,但是以增加PINW为代价。QRLSTM-LF方法在PINW指标上相对较小,其在PICP指标上的效果更差,表明QRLSTM在处理波动性较大的时间序列上易过拟合导致预测效果差的现象。为了详细分析提出预测方法的点负荷预测效果,各种方法的预测结果如图5所示。 图5 不同预测方法的预测曲线图 从图5中可看出,用户用电负荷曲线的“爬坡”和“下坡”阶段相对比较平稳,各种预测方法以上两个阶段具有较好的拟合效果。在用户用电负荷曲线的波动阶段,提出预测方法相比于其它预测方可更好的跟踪负荷曲线,表明了提出预测方法的有效性。为了说明其的概率预测可靠性,选取某天的预测区间进行分析,其预测区间如图6所示。 图6 不同预测方法的预测区间对比图 在图6中可看出,提出预测方法在“爬坡”时期的预测区间相对较窄,虽然在负荷曲线波动时期预测区间相对较宽,但实际值均在预测区间内部,保证了概率预测结果的可靠性。QRLSTM-LF方法虽然锐度较好,但在波动期间存在多处预测区间不能覆盖负荷实际值,不能保证预测结果可靠性。表明提出概率预测方法以较小代价提高概率预测可靠性。 本文提出了一种考虑用户用电行为聚类的电力负荷预测方法。该方法首先采用负荷细粒度数据的分位数自协方差表征用户用电行为特性并使用层次聚类算法进行用户用电行为聚类,然后在聚类的基础上建立电力负荷概率预测,仿真结果验证了QRF算法在用户侧负荷预测上的适用性,并证实了基于分位数自协方差特征的聚类可提高用户聚合体负荷预测精度和可靠性。在下一步研究工作中,将继续关注海量用户聚类过程中的并行处理以及各类用户负荷的影响因素对负荷预测精度的影响。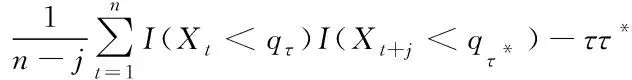

2.2 层级聚类
2.3 轮廓系数

2.4 用户用电行为聚类过程


3 考虑用户用电行为聚类的电力负荷预测
3.1 分位数回归森林算法

3.2 电力负荷预测实现流程




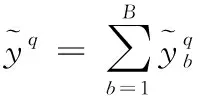
4 实验分析
4.1 用户用电行为聚类分析

4.2 电力负荷预测结果分析
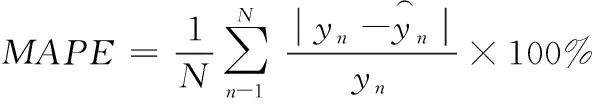


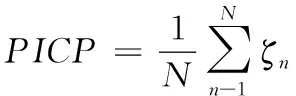
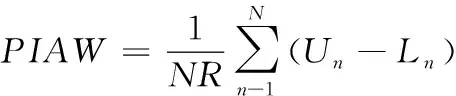
5 总结

